محاسبه تانژانت معکوس – به زبان ساده + مثال

تانژانت معکوس یا آرک تانژانت، یکی از توابع وارون مثلثاتی است که روش‌های مختلفی برای محاسبه آن وجود دارد. از متداول‌ترین روش‌های محاسبه تانژانت معکوس می‌توان به استفاده از ماشین‌حساب مهندسی، ماشین‌حساب ویندوز، تخمین از روی مقادیر معلوم، سری تیلور، ترسیم مثلث قائم‌الزاویه، اکسل و ابزارهای اینترنتی اشاره کرد. در این مطلب از مجله فرادرس، تمام این روش‌ها را آموزش می‌دهیم و برای هر یک از آن‌ها، یک مثال می‌زنیم. در این مطلب ابتدا یاد می‌گیریم که تانژانت معکوس چیست و چگونه محاسبه می‌شود. سپس نحوه محاسبه آن را با ماشین حساب آموزش می‌دهیم و حتی تخمین تانژانت معکوس بدون ماشین حساب را نیز بیان می‌کنیم. در انتها نیز، محاسبه این مقدار را در اکسل و با استفاده از ابزارهای آنلاین آموزش می‌دهیم.

تانژانت معکوس چیست؟

«تابع معکوس یا تابع وارون» (Inverse Function)، تابعی است که عملکرد یک تابع را معکوس می‌کند. فرض کنید یک تابع، با گرفتن مقدار $$a$$ به عنوان ورودی، مقدار $$b$$ را به عنوان خروجی ارائه می‌کند.

به این ترتیب، معکوس این تابع، با گرفتن مقدار $$b$$‌ به عنوان ورودی، مقدار $$a$$ را به عنوان خروجی ارائه خواهد کرد.

تابع تانژانت، یک تابع مثلثاتی است. ورودی توابع مثلثاتی، یک زاویه بوده و خروجی آن‌ها، یک مقدار عددی است. بنابراین، معکوس تابع تانژانت یا به عبارت دیگر، «تانژانت معکوس» (Inverse Tangent)، تابعی است که با گرفتن مقادیر عددی، یک زاویه را به ما می‌دهد. در روابط ریاضی، تانژانت به صورت زیر نشان داده می‌شود:

$$\tan$$

نحوه نمایش تانژانت معکوس یا تانژانت وارون در روابط ریاضی، معمولا به صورت زیر است:

$$\tan ^ { - ۱ }$$

به تانژانت معکوس، آرک‌تانژانت نیز می‌گویند و آن را با $$\arctan$$ نشان می‌دهند. بنابراین، تابع تانژانت معکوس x، عبارت است از:

$$f ( x ) = \tan ^ { - ۱ } ( x ) = \theta$$

یا

$$f ( x ) = \arctan ( x ) = \theta$$

• $$x$$: مقدار تانژانت در زاویه مورد نظر
• $$\theta$$: زاویه مورد نظر

تانژانت معکوس چگونه محاسبه می شود؟

محاسبه تانژانت معکوس، معمولا با استفاده از ماشین حساب و برنامه‌های کامپیوتری انجام می‌شود. البته، اگر تانژانت برخی از زوایا را به خاطر داشته باشید، می‌توانید تانژانت معکوس مقادیر متناظر با آن‌ها را به دست بیاورید. برای درک این موضوع، زوایای زیر را در نظر بگیرید:

$$\theta _ { ۱ } = ۳۰ ^ { \circ }$$

$$\theta _ { ۲ } = ۴۵ ^ { \circ }$$

$$\theta _ { ۳ } = ۶۰ ^ { \circ }$$

تانژانت هر یک از این زوایا برابر است با:

$$\tan \left ( \theta _ { ۱ } \right ) = \tan \left ( ۳۰ ^ { \circ } \right ) = \frac { ۱ }{ \sqrt { ۳ } } \approx ۰/۵۷۷$$

$$\tan \left ( \theta _ { ۱ } \right ) = \tan \left ( ۴۵ ^ { \circ } \right ) = ۱$$

$$\tan \left ( \theta _ { ۱ } \right ) = \tan \left ( ۶۰ ^ { \circ } \right ) = \sqrt { ۳ } \approx ۱/۷۳۲$$

اکنون، با دانستن این تانژانت‌ها، می‌خواهیم مقادیر زیر را به دست بیاوریم:

$$\tan ^ { - ۱ } \left ( ۰/۵۷۷ \right ) = ?$$

$$\tan ^ { - ۱ } \left ( ۱ \right ) = ?$$

$$\tan ^ { - ۱ } \left ( ۱/۷۳۲ \right ) = ?$$

تانژانت معکوس، یک مقدار عددی را به عنوان ورودی دریافت کرده و زاویه متناظر با آن را به عنوان خروجی ارائه می‌دهد. به عنوان مثال، $$\tan ^ { - ۱ } \left ( ۰/۵۷۷ \right )$$ را در نظر بگیرد. باید ببینیم خروجی تانژانت کدام زاویه برابر با ورودی تانژانت معکوس (۰/۵۷۷) می‌شود. با بررسی مقادیر تانژانت‌های ارائه شده، به زاویه ۳۰ درجه می‌رسیم. به عبارت دیگر، چون تانژانت ۳۰ درجه برابر با ۰/۵۷۷ است. تانژانت معکوس ۰/۵۷۷، برابر با ۳۰ درجه خواهد بود. به همین ترتیب داریم:

$$\tan ^ { - ۱ } \left ( ۰/۵۷۷ \right ) = ۳۰ ^ { \circ }$$

$$\tan ^ { - ۱ } \left ( ۱ \right ) = ۴۵ ^ { \circ }$$

$$\tan ^ { - ۱ } \left ( ۱/۷۳۲\right ) = ۶۰ ^ { \circ }$$

مثال ۱: محاسبه تانژانت معکوس صفر

حاصل عبارت زیر را به دست بیاورید:

$$\tan ^ { - ۱ } \left ( ۰ \right ) = ?$$

عبارت بالا، جواب تانژانت معکوس عدد ۰ را از ما می‌خواهد. برای به دست آوردن جواب، زاویه‌ای را پیدا کنیم که تانژانت آن برابر با ۰ می‌شود. این زاویه برابر با ۰ است. چون:

$$\tan\left ( ۰ ^ { \circ } \right ) = ۰$$

از آنجایی که تانژانت زاویه ۰ درجه با مقدار عددی ۰ برابری می‌کند، تانژانت معکوس مقدار عددی ۰ برابر با زاویه ۰ درجه خواهد بود. توجه داشته باشید که اگر در صورت سوال، اشاره‌ای به یکای خروجی تانژانت معکوس نشد، می‌توانید یکای آن را برابر با درجه در نظر بگیرید. به علاوه، می‌توانید از فرمول‌های زیر برای تبدیل زاویه از درجه به رادیان و گرادیان استفاده کنید:

$$radian = \frac { degree \times \pi }{ ۱۸۰ ^ { \circ }}$$

$$gradian = \frac { degree \times ۴۰۰ }{ ۳۶۰ ^ { \circ }}$$

• degree: درجه
• radian: رادیان
• gradian: گرادیان

توجه داشته باشید که علامت خروجی تانژانت زوایای ربع‌های دوم و چهارم دایره مثلثاتی، منفی است. بنابراین، علامت مقدار ورودی تانژانت معکوس، منفی نیز می‌تواند باشد.

محاسبه تانژانت معکوس با ماشین حساب

برخلاف تانژانت معکوس ۰، محاسبه تانژانت زاویه‌های دیگر، نیاز به محاسبات پیچیده و وقت‌گیر دارد. به همین دلیل، اغلب افراد، این محاسبات را با استفاده از ماشین حساب انجام می‌دهند. در این بخش، نحوه محاسبه آرک تانژانت را با استفاده از ماشین حساب واقعی و ماشین حساب ویندوز آموزش می‌دهیم.

محاسبه تانژانت معکوس در ماشین حساب

ساده‌ترین و سریع‌ترین راه برای محاسبه تانژانت معکوس، استفاده از ماشین‌حساب مهندسی است. اغلب ماشین‌حساب‌های مهندسی، کلیدی با عنوان «tan» دارند. این کلید، امکان محاسبه تانژانت را فراهم می‌کند.

در بالای این دکمه، عبارت $$\tan ^ { - ۱ }$$ با یک رنگ دیگر مشخص شده است. همانطور که می‌دانید، این عبارت، تابع تانژانت معکوس را نمایش می‌دهد. به دلیل نوشته شدن عنوان تانژانت معکوس در بالای دکمه اصلی، برای فعال کردن آن باید از کلید ترکیبی «SHIFT» استفاده کنیم. این کلید معمولا در ردیف بالایی ماشین‌حساب‌های مهندسی قرار دارد و توابع نوشته شده به رنگ خود را فعال می‌کند (در اینجا، توابع زرد رنگ).

در برخی از ماشین حساب‌ها، به جای دکمه SHIFT، دکمه‌ای با عنوان $$2nd$$ وجود دارد که عملکرد آن، مشابه SHIFT است. به عنوان مثال، می‌خواهیم آرک تانژانت ۱ را با ماشین حساب مهندسی محاسبه کنیم. برای این کار، ابتدا کلید SHIFT را فشار می‌دهیم. با این کار، یک علامت کوچک در بالای صفحه ظاهر می‌شود که فعال شدن SHIFT را نمایش می‌دهد. سپس، دکمه tan را می‌فشاریم تا عبارت زیر در صفحه ماشین‌حساب ظاهر شود:

$$\tan ^ { - ۱ } ($$

پس از مشاهده تانژانت معکوس در ماشین‌حساب، دکمه عدد ۱ و سپس دکمه بستن پرانتز را انتخاب می‌کنیم.

با فشردن کلید مساوی ($$=$$)، نتیجه تانژانت معکوس ۱ در صفحه ماشین‌حساب ظاهر می‌شود. یکای خروجی ماشین‌حساب، به تنظیمات آن بستگی دارد. اگر این یکا بر روی درجه تنظیم شده باشد، جواب $$۴۵ ^ { \circ }$$ به نمایش درمی‌آید. در صورت تنظیم بودن یکای زاویه بر روی رادیان یا گرادیان، مقادیر متناظر با آن‌ها نشان داده می‌شود.

محاسبه تانژانت معکوس در ماشین حساب ویندوز

یکی از سریع‌ترین و راه‌ترین روش‌های محاسبه آرک تانژانت، بدون نیاز به ماشین‌حساب واقعی یا ماشین‌حساب‌های آنلاین، استفاده از ماشین حساب ویندوز است که در ادامه به آموزش آن می‌پردازیم. ماشین‌حساب ویندوز را باز کنید. برای این کار می‌توانید پس از فشردن کلید ویندوز بر روی صفحه‌کلید یا کلیک بر روی آیکون استارت در قسمت پایین-چپ صفحه، عبارت «Calculator» را تایپ کنید.

بر روی آیکون ماشین حساب کلیک کنید تا باز شود. اگر تنظیمات ماشین‌حساب را تغییر نداده باشید، این ابزار به صورت زیر به نمایش درمی‌آید.

برای انجام محاسبات مثلثاتی، باید ماشین‌حساب ویندوز را بر روی حالت علمی قرار دهیم. به این منظور، بر روی علامت سه‌خط در قسمت بالا-چپ کلیک کرده و گزینه «Scientific» را انتخاب می‌کنیم.

با این کار، رابط کاربری ماشین‌حساب ویندوز به شکل زیر درمی‌آید.

به این ترتیب، گزینه‌های بیشتری به ماشین‌حساب افزوده می‌شوند. یکی از این گزینه‌ها، «Trigonometry» است که امکان انجام محاسبات مثلثاتی را فراهم می‌‌کند.

پیش از استفاده از این گزینه‌ها، اشاره به چند نکته ضروری است. هنگام وارد کردن زاویه در ماشین‌حساب ویندوز، باید از مطابقت یکای عدد وارد شده با یکای فعال در ماشین‌حساب اطمینان حاصل کنید. یکای زاویه در ماشین‌حساب، در تصویر زیر نمایش داده شده است. این یکا را می‌توان روی حالت «DEG» برای نوشتن بر حسب درجه، «RAD» برای نوشتن بر حسب رادیان یا «GRAD» برای نوشتن بر حسب گرادیان تنظیم کرد.

نکته بعدی، ترتیب وارد کردن عدد و انجام محاسبات است. برخلاف اغلب ماشین‌حساب‌های واقعی یا برنامه‌های آفلاین و آنلاین، در اینجا، ابتدا باید عدد مورد نظر خود را وارد کنیم و سپس با فشردن تابع مورد نظر، نتیجه را به دست بیاوریم. به عنوان مثال، برای تعیین تانژانت معکوس ۰/۵، ابتدا این عدد را در ماشین‌حساب ویندوز تایپ می‌کنیم.

مرحله بعد، انجام عملیات ریاضی بر روی مقدار تایپ شده است. به این منظور، با کلیک بر روی Trigonometry، فهرست توابع مثلثاتی را باز می‌کنیم.

در حالت پیش‌فرض پنجره توابع مثلثاتی، خبری از تانژانت وارون نیست. برای مشاهده این تابع، بر روی $$۲ ^ { n d }$$ کلیک می‌کنیم.

به این ترتیب، توابع معکوس مثلثاتی به نمایش درمی‌آیند. با کلیک بر روی تانژانت معکوس ($$\tan ^ { - ۱ }$$)، آرک تانژانت ۰/۵ بر حسب زاویه محاسبه می‌شود.

تخمین تانژانت معکوس بدون ماشین حساب

در ادامه این مطلب از مجله فرادرس، به معرفی برخی از مقادیر تانژانت معکوس در قالب یک جدول می‌پردازیم. این جدول، برای زاویه‌های ۰ تا ۹۰ درجه تهیه شده است.

در بسیاری از سوالات امتحانی و حتی مسائل واقعی، ممکن است با این مقادیر رو به رو شوید. علاوه بر این، در صورتی که با این تانژانت‌های معکوس آشنایی داشته باشید، می‌توانید جواب مسائل مرتبط را به صورت تخمینی و با تقریب نسبتا خوبی به دست بیاورید.

همان‌طور که مشاهده می‌کنید، برای مقادیر کوچک (حدودا کوچک از ۰/۲۷)، با تقریب نسبتا خوبی می‌توان تانژانت معکوس را برابر با همان مقدار بر حسب رادیان در نظر گرفت. اگر مقداری که قصد محاسبه تانژانت معکوس آن را دارید، نزدیک به ۶۰ یا بزرگ‌تر از آن باشد، می‌توانید جواب را بین ۸۹ تا ۹۰ درجه در نظر بگیرید.

مقادیر معرفی شده در جدول بالا، متعلق به ربع اول دایره مثلثاتی هستند. برای ربع‌های دوم، سوم و چهارم، با رعایت اصول تعیین علامت نسبت‌های مثلثاتی می‌توان مقادیر تانژانت معکوس را به دست آورد.

زوایای ۰، ۱۵، ۳۰، ۴۵، ۶۰ و ۷۵، به عنوان زوایای پرکاربرد و مهم در نظر گرفته می‌شوند. تانژانت‌های معکوس مرتبط با این زوایا را حفظ کنید. علاوه بر این، زوایای ۵۳، ۳۷ و ۲۲/۵ درجه، از زوایای پرکاربرد در سوالات امتحانی، مخصوصا امتحانات دبیرستان هستند. بنابراین، بهتر است با تانژانت معکوس متناظر با این زوایا نیز آشنا باشید:

$$\tan ^ { -۱ } ( ۱/۳۲۷ ) = ۵۳ ^ { \circ }$$

$$\tan ^ { -۱ } ( ۰/۷۵۳ ) = ۳۷ ^ { \circ }$$

$$\tan ^ { -۱ } ( ۰/۴۱۴ ) = ۲۲/۵ ^ { \circ }$$

به خاطر داشته باشید که تانژانت معکوس بی‌نهایت برابر با ۹۰ درجه یا $$\frac { \pi } { 2 }$$ است. در اغلب موارد، محاسبه تانژانت معکوس با استفاده از ماشین حساب صورت می‌گیرد. با این وجود، در شرایطی که دسترسی به ماشین‌حساب یا ابزارهای محاسبه آنلاین وجود ندارد، می‌توان با استفاده از تخمین، یک دید کلی از بازه موجه جواب به دست آورد. این موضوع را با یک مثال توضیح می‌دهیم.

مثال ۲: تخمین تانژانت معکوس

تانژانت معکوس ۰/۹ را تخمین بزنید.

برای تخمین آرک تانژانت ۰/۹، باید به دنبال زاویه‌ای بگردیم که تانژانت آن با مقدار ۰/۹ برابری کند. از جدول ارائه شده در ابتدای این بخش، تانژانت معکوس متناظر با دو زاویه ۴۰ و ۴۵ درجه را داریم:

$$\tan ^ { -۱ } (۰/۸۳۹) = ۴۰ ^ { \circ }$$

$$\tan ^ { -۱ } (۱) = ۴۵ ^ { \circ }$$

بر اساس این مقادیر، تانژانت معکوس ۰/۹ بین ۴۰ تا ۴۵ درجه خواهد بود. برای تخمین آرک تانژانت با استفاده از جدول، تا همین حد می‌توانیم پیش برویم. در ادامه، یک روش دقیق‌تر و بدون نیاز به ماشین حساب را برای محاسبه تانژانت معکوس آموزش می‌دهیم.

محاسبه تانژانت معکوس بدون ماشین حساب به روش سری

یکی از بهترین و دقیق‌ترین روش‌های محاسبه آرک تانژانت بدون ماشین حساب، استفاده از سری تیلور است. سری تیلور برای تانژانت وارون به صورت زیر نوشته می‌شود:

$$\tan ^ { -۱ } ( x ) = x - \frac {x ^ ۳}{ ۳ } + \frac { x ^ ۵ }{ ۵ } - \frac { x ^ ۷ }{ ۷ } + \ ...$$

مثال ۲ را در نظر بگیرید. در این مثال، می‌خواستیم تانژانت معکوس ۰/۹ را به دست بیاوریم. اگر این مقدار را درون رابطه بالا قرار دهیم، و آن را تا عبارت سوم حل کنیم، خواهیم داشت:

$$\tan ^ { -۱ } ( x ) = ۰/۹ - \frac { ۰ / ۹ ^ ۳}{ ۳ } + \frac { ۰ / ۹ ^ ۵ }{ ۵ } \approx ۰/۷۷۵$$

جواب به دست آمده از این رابطه بر حسب رادیان است. با استفاده از فرمول زیر، مقدار به دست آمده را به درجه تبدیل می‌کنیم:

$$radian = \frac { degree \times \pi }{ ۱۸۰ ^ { \circ }}$$

$$۰/۷۷۵ = \frac { degree \times \pi }{ ۱۸۰ ^ { \circ }}$$

$$degree = \frac { ۰/۷۷۵ \times ۱۸۰ ^ { \circ } }{ ۳/۱۴ }$$

$$degree = ۴۴/۴ ^ { \circ }$$

جواب بالا، مقدار دقیق تانژانت معکوس ۰/۹ نیست. با این وجود، به جواب دقیق نزدیک‌تر است. با محاسبه عبارت‌های بیشتر سری تیلور، می‌توانیم به جواب واقعی نزدیک شویم. با این وجود، این کار، محاسبات را بیشتر و پیچیده‌تر می‌کند تا جایی که دیگر نمی‌توان از ماشین حساب استفاده نکرد.

تعیین تانژانت معکوس بدون ماشین حساب به روش ترسیمی

یکی دیگر از روش‌های به دست آوردن تانژانت معکوس بدون ماشین حساب، توسط خط‌کش و نقاله است. برای این کار، ابتدا با استفاده از رابطه نسبت مثلثاتی تانژانت، یک مثلث قائم‌الزاویه می‌سازیم. مثال ۲ را دوباره در نظر بگیرید. هدف این مثال، تعیین آرک تانژانت ۰/۹ بود.

اکنون، تعریف تانژانت در مثلث قائم‌الزاویه را به خاطر بیاورید. بر اساس این تعریف، تانژانت یک زاویه، برابر با نسبت اندازه ضلع مقابل به آن زاویه بر روی اندازه ضلع مجاور به آن زاویه است:

$$\tan ( \theta ) = \frac { O }{ A }$$

• $$\theta$$: زاویه مورد نظر
• $$O$$: ضلع مقابل زاویه $$\theta$$
• $$A$$: ضلع مجاور زاویه $$\theta$$

بر اساس این نسبت مثلثاتی، داریم:

$$\tan ( \theta ) = \frac { O }{ A } = ۰/۹$$

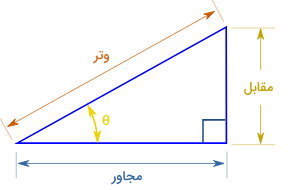
به این ترتیب، اگر مثلث قائم‌الزاویه‌ای را رسم کنیم که در آن، نسبت ضلع مقابل به مجاور برابر با ۰/۹ باشد، امکان تعیین زاویه $$\theta$$ با استفاده از نقاله فراهم می‌شود. مقادیر ضلع‌های مقابل به مجاور را به صورت دلخواه اما با رعایت نسبت انتخاب کنید. مثلا می‌توانید ضلع مقابل را برابر با ۹ سانتی‌متر و ضلع مجاور را برابر با ۱۰ سانتی‌متر در نظر بگیرید. سپس، مثلث قائم‌الزاویه‌ای با ساق‌هایی به اندازه ۹ و ۱۰ سانتی‌متر را رسم کنید.

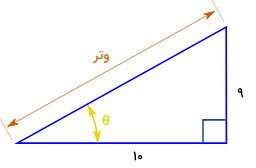
اکنون با تنظیم نقاله بر روی راس مورد نظر، زاویه $$\theta$$ تعیین می‌شود. این زاویه، برابر با ۴۲ درجه است. استفاده از این روش، به دقت در ترسیم و اندازه‌گیری توسط خط‌کش و نقاله بستگی دارد. در برخی از مواقع نیز، به دلیل وجود رقم‌های زیاد بعد از اعشار، امکان رسم مثلث با نسبت‌های دقیق وجود ندارد. در ادامه، نحوه استفاده از ابزارهای کامپیوتری آفلاین و آنلاین را برای محاسبه تانژانت معکوس آموزش می‌دهیم.

محاسبه تانژانت معکوس در اکسل

«اکسل» (Excel)، محبوب‌ترین نرم‌افزار صفحه گسترده است که معمولا به منظور انجام محاسبات و تهیه گزارش‌های عددی مورد استفاده قرار می‌گیرد. از قابلیت‌های کاربردی این نرم‌افزار می‌توان به وجود توابع ریاضی متعدد اشاره کرد.

یکی از توابع ریاضی در اکسل، تابع ATAN است که امکان محاسبه تانژانت معکوس را فراهم می‌کند. به منظور محاسبه آرک تانژانت در اکسل، ابتدا این نرم‌افزار را باز کرده و بر روی یکی از سلول‌های خالی کلیک کنید.

کادری که در بالای سلول‌ها وجود دارد (کادر $$f _ x$$)، مخصوص فرمول‌نویسی و استفاده از توابع در اکسل است. هنگامی که یک سلول را انتخاب می‌کنید، امکان وارد کردن عدد، حرف یا فرمول در آن فراهم می‌شود. پس از انتخاب سلول مورد نظر، ابتدا یک علامت مساوی (= ) و سپس عبارت ATAN را تایپ کنید.

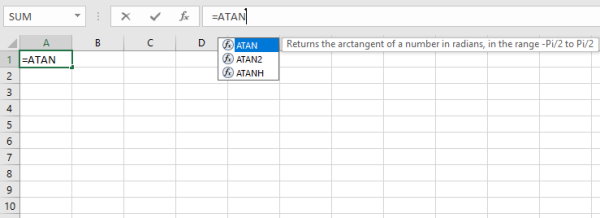
در انتهای عنوان تابع تانژانت معکوس، یک علامت پرانتز باز قرار دهید. با این کار، نرم‌افزار از شما می‌خواهید تا عددی را وارد کنید که می‌خواهید تانژانت معکوس آن را به دست بیاورید.

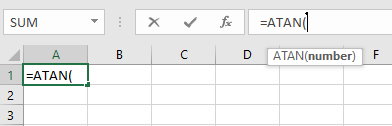
در مثال ۲، قصد داشتیم تانژانت وارون ۰/۹ را به دست بیاوریم. همین عدد را داخل پرانتز می‌نویسیم و بعد از بستن آن، کلید Enter را فشار می‌دهیم.

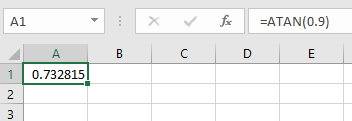
پس از فشردن Enter، جواب تانژانت معکوس ۰/۹ در سلول به نمایش درمی‌آید. خروجی تابع ATAN در اکسل، عددی با یکای رادیان است. اگر می‌خواهید این جواب را بر حسب رادیان مشاهده کنید، تابع DEGREES را در یک سلول خالی بنویسید.

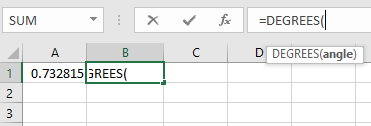
اکسل از شما می‌خواهد تا زاویه مورد نظر خود یا سلول حاوی این زاویه را درون پرانتز مشخص کنید. برای این کار، نشانگر ماوس را بر روی سلول حاوی مقدار زاویه ببرید و بر روی آن کلیک کنید.

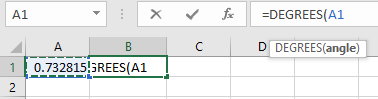
پس از ظاهر شدن عنوان سلول حاوی مقدار زاویه در تابع، پرانتز را ببندید و کلید Enter را فشار دهید. به این ترتیب، تانژانت معکوس ۰/۹ به صورت زاویه‌ای با یکای درجه به نمایش درمی‌آید.

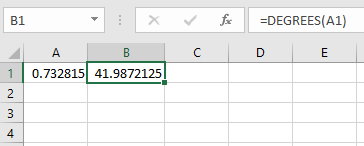
همان‌طور که مشاهده می‌کنید، تانژانت معکوس ۰/۹ برابر با ۴۱/۹۸۷ درجه است. اکسل، به عنوان یکی از نرم‌افزارهای عمومی با قابلیت محاسبه توابع ریاضی، همواره جواب‌های دقیق را با سرعت بالا ارائه می‌کند.

محاسبه تانژانت معکوس آنلاین

سایت‌های مختلفی برای محاسبه آنلاین تانژانت معکوس وجود دارد. برخی از بهترین سایت‌ها در این زمینه عبارت هستند از:

• Wolfram Alpha (+)
• Thetawise (+)
• Symbolab (+)
• Math Solver (+)

سایت‌های بالا، از ابزارهای هوش مصنوعی برای حل مسائل ریاضی استفاده می‌کنند. علاوه بر این سایت‌ها، موتور جستجوی گوگل نیز ابزار مناسبی برای محاسبه آرک تانژانت است. در اینجا، از سایت «Wolfram Alpha» برای حل یک مثال استفاده می‌کنیم. با رفتن به این سایت، با صفحه‌ای مشابه تصویر زیر روبه‌رو می‌شوید.

Wolfram Alpha، هم امکان نوشتن سوال به زبان طبیعی و هم نوشتن سوال به زبان ریاضی را فراهم کرده است. برای طرح مسئله به زبان ریاضی، بر روی دکمه «MATH INPUT» کلیک می‌کنیم تا صفحه کلید مخصوص این کار به نمایش درآید.

تابع مخصوص محاسبه تانژانت معکوس با کلید $$\tan ^ { - ۱ } \square$$ در بخش «TRIGONOMETRY» قرار دارد.

با کلیک بر روی $$\tan ^ { - ۱ } \square$$، تابع تانژانت معکوس در کادر تایپ فرمول ظاهر می‌شود.

به عنوان مثال، عدد $$۰/۱$$ را درون پرانتز می‌نویسیم و کلید Enter را فشار می‌دهیم یا بر روی دکمه مساوی کلیک می‌کنیم.

به این ترتیب، جواب سوال به روش‌های مختلف و با یکاهای متفاوت به نمایش درمی‌آید. یکی از قابلیت‌های جالب Wolfram Alpha، حل مسئله به صورت گام به گام و به چندین روش است. به عنوان مثال، در اینجا، تانژانت معکوس با استفاده از روش‌های سری، انتگرال و دیگر روش‌های پیشرفته حل شده است.

سوالات متداول در رابطه با محاسبه تانژانت معکوس

در آخرین بخش از این مطلب مجله فرادرس، به برخی از پرتکرارترین سوالات مرتبط با محاسبه تانژانت معکوس به طور مختصر پاسخ می‌دهیم.

نام دیگر تانژانت معکوس چیست؟

تانژانت معکوس، با عنوان آرک تانژانت نیز شناخته می‌شود. بنابراین، منظور از محاسبه آرک تانژانت، همان محاسبه تانژانت معکوس است.

برای محاسبه تانژانت معکوس به چه ماشین حسابی نیاز داریم؟

به منظور محاسبه آرک تانژانت یا همان تانژانت معکوس، به یک ماشین‌حساب مهندسی نیاز داریم.

چگونه تابع تانژانت معکوس را در ماشین حساب مهندسی فعال کنیم؟

برای فعال‌سازی تابع تانژانت وارون در ماشین‌حساب مهندسی، به ترتیب کلید SHIFT و کلید tan را فشار دهید تا عبارت مخصوص این تابع در صفحه نمایش ظاهر شود.

چگونه تابع تانژانت معکوس را در ماشین حساب ویندوز فعال کنیم؟

برای فعال‌سازی تابع تانژانت وارون در ماشین‌حساب ویندوز، پس از کلیک بر روی دکمه Trigonometry، گزینه ۲nd را انتخاب کنید تا توابع معکوس مثلثاتی، از جمله تانژانت معکوس ظاهر شوند.

آیا می توان تانژانت معکوس را بدون ماشین حساب محاسبه کرد؟

بله. روش‌های مختلفی برای تعیین تانژانت معکوس بدون ماشین حساب وجود دارد. البته این روش‌ها، به سادگی کار با ماشین‌حساب نیستند.

روش های محاسبه آرک تانژانت بدون ماشین حساب چه هستند؟

از متداول‌ترین روش‌های محاسبه تانژانت معکوس بدون ماشین حساب می‌توان به روش ترسیمی (رسم مثلث قائم‌الزاویه و اندازه‌گیری زاویه با نقاله)، روش فرمولی (سری تیلور یا دیگر روابط ریاضی)، استفاده از نرم‌افزارهای محاسباتی (مانند اکسل)، استفاده از سایت‌های اینترنتی و تخمین از روی مقادیر معلوم اشاره کرد.

از کدام سری می توان برای محاسبه آرک تانژانت استفاده کرد؟

از سری‌های قابل استفاده برای محاسبه تانژانت معکوس می‌توان سری تیلور را نام برد.

تابع آرک تانژانت در اکسل چیست؟

تابع مربوط به محاسبه تانژانت معکوس در اکسل، ATAN است.

روش ترسیمی محاسبه آرک تانژانت چیست؟

روش ترسیمی محاسبه تانژانت معکوس، ابتدا یک مثلث قائم الزاویه را به گونه‌ای رسم می‌کنیم که نسبت ساق‌های آن برابر با عدد درون تانژانت معکوس باشد. سپس، با استفاده از نقاله، زاویه مورد نظر را به دست می‌آوریم.

بهترین سایت های محاسبه آرک تانژانت چه هستند؟

ولفرام آلفا، سیمبولب، مث سالور و گوگل، برخی از بهترین سایت‌ها و ابزارهای آنلاین برای محاسبه تانژانت معکوس هستند.