تابع دلتای کرونکر و خواص آن | به زبان ساده

در ریاضیات، توابع نقش مهمی در بیان رابطه بین متغیرها دارند. رفتار بیشتر پدیده‌های طبیعی را می‌توان به صورت یک تابع مشخص کرد. در این بین تابع دلتای کرونکر (Kronecker Delta) یک تابع خاص است که اغلب برای اعداد طبیعی (صحیح نامنفی) به کار می‌رود. تابع دلتای کرونکر در حقیقت شبیه یک «تابع نشانگر» (Indicator Function) عمل می‌کند تا برابری دو متغیر را نشان دهد. در این نوشتار از مجله فرادرس به بررسی تابع دلتای کرونکر و خواص آن خواهیم پرداخت. این تابع به افتخار معرفی کننده آن، «لئوپولد کرونکر» (Leopold kronecker)، ریاضیدان آلمانی قرن ۱۹، تابع دلتای کرونکر نامیده شده است.

به منظور آشنایی بیشتر با مفاهیم به کار رفته در این متن بهتر است نوشتارهای ضرب داخلی بردارها — به زبان ساده و تابع دلتای دیراک — به زبان ساده را مطالعه کنید. همچنین خواندن مطالب اعداد گویا — به زبان ساده و تابع نشانگر و خصوصیات آن — به زبان ساده نیز خالی از لطف نیست.

تابع دلتای کرونکر

«تابع دلتای کرونکر» (Kronecker Delta Function) یک تابع دو متغیره است که معمولا براساس مقادیر صحیح نامنفی محاسبه می‌شود. این تابع در صورت برابری دو متغیر آن، برابر با یک و در غیر اینصورت مقدار صفر را خواهد داشت.

$$ \large \delta _{{ij}} = {\begin{cases} 0 & {\text{if }} i \neq j , \\ 1 & {\text{if }} i = j \end{cases}} $$

نکته: گاهی تابع دلتای کرونکر را به صورت «براکت ایروسن» (Iverson Brackets) نشان می‌دهند.

$$ \large {\displaystyle \delta _{ij} = [i = j] \,} $$

برای مثال مقدار دلتای کرونکر برای $$\delta_{1 \ 2} $$ برابر با صفر ولی برای $$\delta_{ 3\ 3} $$ برابر با ۱ است.

البته شرط صحیح (نامنفی) بودن متغیرهای این تابع می‌تواند برداشته شده و برای اعداد گویا و منفی نیز تعریف قبلی به کار برده شود. به این ترتیب رابطه‌های زیر را خواهیم داشت.

$$ \large {\displaystyle {\begin{aligned}\delta_{(-1)(-3)}& = 0 & \qquad \delta _{(- 2)(- 2)} & = 1 \\ \delta_{\left({\frac {1}{2}}\right) \left(-{\frac{3}{2}} \right)}& = 0 & \qquad \delta_{\left({ \frac {5}{3}} \right) \left( {\frac {5}{3}} \right) } & = 1 \end{aligned}}} $$

نکته: متاسفانه تابع دلتای کرونکر برای «اعداد مختلط» (Complex Numbers) به کار برده نمی‌شود.

یک شیوه دیگر نیز برای نمایش تابع دلتای کرونکر وجود دارد که از یک پارامتر بهره می‌برد. به این ترتیب تابع دلتای کرونکر را به صورت $$\delta_i$$ نشان داده و در حقیقت پارامتر $$j$$ را برابر با صفر در نظر می‌گیرند. در این حالت تابع دلتای کرونکر به شکل زیر حاصل می‌شود.

$$ \large\delta_{i} = \begin{cases} 0, & \mbox{if } i \ne 0 \\ 1, & \mbox{if } i=0 \end{cases}$$

تابع دلتای کرونکر در بسیاری از موارد و حوزه‌های مربوط به فیزیک و مهندسی نیز ظاهر می‌شود. برای مثال، در جبر خطی (Linear Algebra)، می‌توان «ماتریس یکه» یا «ماتریس همانی» (Identity Matrix) که یک ماتریس مربعی $$n \times n$$ است را برحسب تابع دلتای کرونکر نمایش داد.

$$ \large {\displaystyle I_{ij}=\delta _{ij}}, \;\;i , j = 1 , 2, , \ldots , n$$

حتی «ضرب داخلی بردارهای» (Inner Product) برحسب تابع دلتای کرونکر قابل تعیین است. فرض کنید که $$a$$ و $$b$$ دو بردار باشند. در این صورت ضرب داخلی آن‌ها را با استفاده از تابع دلتای کرونکر به صورت زیر می‌توان نوشت:

$$ \large{\displaystyle \mathbf {a} \cdot \mathbf {b} =\sum _{i,j=1}^{n}a_{i}\;\; \delta _{ij} \;\; b_{j}}$$

نکته: تابع دلتای کرونکر را به کمک تابع نمایی و عدد مختلط واحد ($$i^2 = – 1$$) به صورت مجموع یک دنباله نیز می‌توان نشان داد که برگرفته از «سری هندسی متناهی» (Finite Geometric Series) است.

$$ \large {\displaystyle \delta_{nm} = { \frac {1}{N}} \sum_{k = 1}^{N}e^{2\pi i{\frac {k}{N}}(n – m)}}$$

خواص تابع دلتای کرونکر

خواص زیر برای تابع دلتای کرونکر در نظر گرفته می‌شوند. البته توجه داشته باشید که مقدار $$a_i$$، یک عدد حقیقی است.

• $$ \large \sum_{j} \delta_{ij} a_j = a_i $$
• $$ \large \sum_{i} a_i\delta_{ij}  = a_j $$
• $$\large \sum_{k} \delta_{ik}\delta_{kj}  = \delta_{ij} $$

با توجه به رابطه‌های بالا می‌توان ماتریس $$\delta$$ را به صورت یک ماتریس یکه در نظر گرفت. همچنین اگر $$j \in Z$$ یعنی «اعداد صحیح» (Whole Numbers) باشد، تابع دلتای کرونکر در رابطه زیر صدق خواهد کرد.

$$ \large \sum_{ i = – \infty}^\infty a_i \delta_{ij} = a_j$$

این خاصیت را به نام «غربالگری» (Sifting) می‌شناسیم.

اگر اعداد صحیح (نامنفی) را به صورت یک «فضای اندازه» (Measure Space) در نظر بگیریم، ویژگی ذکر شده با خاصیت «تابع دلتای دیراک» (Dirac delta function) برابر خواهد شد. در نتیجه داریم:

$$ \large {\displaystyle \int _{-\infty }^{\infty } \delta (x – y) f(x)\,dx = f(y)} $$

ممکن است در بعضی از حوزه‌ها که نماد یکسانی برای تابع دلتای کرونکر و تابع دلتای دیراک استفاده می‌شود، این دو تابع با یکدیگر اشتباه شوند. در مباحث مربوط به «پردازش سیگنال» (Signal Processing)، چه در محیط زمان-گسسته یا زمان-پیوسته (Discrete or Continuous time)، تفاوت تابع دلتای کرونکر و دیراک بستگی به محتوای مورد بحث دارد.

معمولا نماد $$\delta(t)$$ برای مشخص کردن تابع دلتای دیراک در حالت زمان-پیوسته به کار می‌رود. در حالیکه نماد برای پارامترهای تابع اگر به شکل $$i, j , k , l , m ,n$$ باشند، منظور تابع دلتای کرونکر بوده و مرتبط با سیگنال‌های زمان-گسسته است.

نکته: تابع دلتای دیراک، تابعی است که در سه خاصیت زیر صدق کند. اغلب در پردازش سیگنال برای نمایش حالت زمان-گسسته، تابع دلتا را به صورت $$\delta[n]$$ نشان می‌دهند.

$$ \large \delta \left [ { t – a } \right ] = 0 , \, \, \, \, t \ne a $$

$$ \large \displaystyle \int _ { { \, a – \varepsilon } } ^ { { \, a + \varepsilon } } { { \delta \left [ { t – a } \right ] \, d t } } = 1 , \hspace {0.25in} \varepsilon > 0 $$

$$ \large \displaystyle \int _ { { \, \, a – \varepsilon } } ^ { { \, \, a + \varepsilon } } { { f \left ( t \right ) \delta \left [ { t – a } \right ] \, d t } } = f \left ( a \right ) , \hspace {0.25in} \, \, \, \, \, \, \, \, \, \varepsilon > 0 $$

به یاد داشته باشید که نمونه‌گیری مستقیم از تابع دلتای دیراک منجر به تولید تابع دلتای کرونکر نمی‌شود. بلکه این کار باید تحت قیود مشخصی صورت گیرد.

کاربرد تابع دلتای کرونکر در پردازش سیگنال

در مطالعه «پردازش سیگنال دیجیتال» (Digital Signal Processing) یا به اختصار DSP، «تابع دلتای نمونه‌گیری واحد» (Unit Sample Function) که با نماد $$ {\displaystyle \delta [n] }$$ مشخص می‌شود، نمایانگر مورد ویژه‌ای از «تابع دو پارامتری دلتای کرونکر» ($${\displaystyle \delta_{ij}}$$) است، به طوری که یکی از پارامترها صفر است. در این مورد خواهیم داشت:

$$ \large {\displaystyle \delta [n – k] \equiv \delta [k – n] \equiv \delta_{n k} \equiv \delta _{k n}} $$

بطوری که

$$\large {\displaystyle – \infty < n < \infty , – \infty < k < \infty } $$

در مباحث مربوط به «تانسورها» (Tensor)، معمولاً تعداد بردارهای پایه در ابعاد خاص به جای اندیس صفر از اندیس 1 شروع می‌شوند. در این حالت رابطه $$ { \displaystyle \delta [n] \equiv \delta_ {n 0} \equiv \delta_ {0 n}} $$ وجود ندارد.

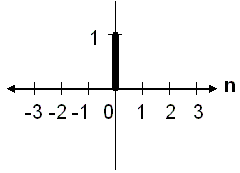
در واقع، تابع دلتای کرونکر و «تابع نمونه‌گیری واحد» (Unit Sample function) توابع مختلفی هستند که به طور اتفاقی در یک مورد خاص با یکدیگر همپوشانی دارند. واضح است که در این حالت زیرنویس‌ یا اندیس‌ها ممکن است رقم صفر (0) را شامل شوند. در این وضعیت دو اندیس یا زیرنویس وجود داشته که یکی از آن‌ها حتما مقدار صفر خواهد داشت.

هر چند «تابع نمونه‌گیری واحد زمان-گسسته» (Discrete Unit Sample Function) و تابع «دلتا کرونکر» از نماد یکسانی استفاده می‌کنند ولی با یکدیگر تفاوت‌هایی دارند. برای تابع نمونه‌گیری واحد زمان-گسسته، معمولا از نماد براکت و یک عدد صحیح استفاده می‌شود. در مقابل برای تابع دلتای کرونکر، اعداد به صورت زیرنویس یا اندیس در کنار علامت $$\delta$$ قرار می‌گیرند.

از طرفی، هدف از به کارگیری «تابع نمونه واحد زمان-گسسته» با هدف از به کارگیری «تابع دلتای کرونکر» تفاوت دارد. در DSP، از تابع نمونه واحد گسسته معمولاً به عنوان یک تابع ورودی به یک سیستم گسسته برای کشف «تابع سیستم» (System Function) سامانه استفاده می‌شود که خروجی‌ها توسط آن تولید شده‌اند.

از دیدگاه استراتژیک، هدف اصلی در استفاده از تابع دلتا کرونکر، فیلتر کردن جملات از «مجموع انیشتین» (Eisenstein Summation) است و هر یک از اندیس‌های تابع دلتا کرونکر یک بُعد را در یک مجموعه پایه نشان می‌دهند.

نکته: مجموع اینشتین، به مجموع متناهی در یک میدان متناهی گفته می‌شود که مرتبط با «مجموع گاوسی» (Gauss Sum) است.

تابع نمونه‌گیری گسسته به شکل ساده، مطابق با رابطه زیر تعریف می‌شود:

$$ \large {\displaystyle \delta [n] = {\begin{cases} 1 & n = 0 \\ 0 & {\text{otherwise}} \end{cases}}} $$

علاوه بر این، در مباحث مربوط به DSP تابعی به نام تابع دلتای دیراک نیز به کار می‌رود که اغلب با دو تابع دیگر یعنی تابع دلتا کرونکر و تابع نمونه‌گیری واحد اشتباه گرفته می‌شود. توجه داشته باشید که تابع دلتای دیراک به صورت زیر معرفی می‌شود.

$$ \large {\displaystyle \delta (t) = {\begin{cases} \infty & t = 0 \\ 0 &{\text{otherwise}} \end{cases}}}$$

به این موضوع نیز توجه داشته باشید که بر خلاف تابع دلتا کرونکر $$ {\displaystyle \delta_{ij}} $$ و «تابع نمونه‌گیری واحد» $${\displaystyle \delta [n]} $$، تابع دلتای دیراک $$ {\displaystyle \delta (t) }$$ دارای پارامتر با مقدار صحیح نیست، بلکه مقادیر پیوسته را به عنوان متغیر می‌پذیرد.

ارتباط تابع دلتای کرونکر با دلتای دیراک

در نظریه احتمال و آمار، تابع دلتای کرونکر و دلتای دیراک می‌توانند برای بیان یک «تابع توزیع گسسته» (Discrete Distribution) به کار روند. اگر تکیه‌گاه توزیع شامل نقاطی به صورت $$S_X = \{x_1, x_2 ,\ldots, x_n\}$$ با احتمالات $$p_1, p_2 , \ldots, p_n$$ باشد، آنگاه تابع جرم احتمال (Probability Mass Function) یا به طور خلاصه تابع احتمال $$p(X)$$ را روی $$S_X$$ به صورت زیر و به کمک تابع دلتای کرونکر نشان می‌دهند.

$$ \large p(x) = \sum_{i = 1}^n p_i \delta_{x – x_i}$$

منظور از $$\delta_{x-x_i}$$، همان تابع دلتای کرونکر تک پارامتری است.

در صورتی که متغیر تصادفی $$X$$، دارای تابع چگالی پیوسته (Continuous) یا تابع چگالی احتمال (Probability Density Function) به شکل $$f(x)$$ باشد، آنگاه می‌توان رابطه زیر را برای آن نوشت.

$$ \large f(x)=\sum _{i = 1}^{n}p_{i}\delta (x – x_{i})$$

که در آن $$\delta(x – x_i)$$، همان تابع دلتای دیراک است.

تحت شرایط خاص، دلتا کرونکر می‌تواند حاصل یک نمونه‌گیری از تابع دلتای دیراک باشد. به عنوان مثال، اگر یک ضربان دلتا دیراک، دقیقاً در یک نقطه نمونه‌گیری و از «فیلتر پایین گذر ایده‌آل» (Ideally Lowpass-filter) عبور داده شود (با شرط قطع در فرکانس بحرانی)، طبق «قضیه نمونه‌برداری شانون-نیکوئیت» (Nyquist-Shannon Sampling Theorem)، سیگنال ایجاد شده یک سیگنال زمان-گسسته بوده که همان تابع دلتای کرونکر خواهد بود.

خلاصه و جمع‌بندی

در این نوشتار به بررسی تابع دلتای کرونکر و خواص آن پرداختیم. مشخص شد که در بعضی از حالات، دو تابع دلتای کرونکر و دلتای دیراک برابر هستند و نقش یکسانی در بعضی از حوزه‌های علوم دارند. نقش تابع دلتای دیراک برای توصیف پدیده‌هایی زمان-گسسته در فیزیک و الکتریسیته و حتی نظریه احتمال دیده می‌شود. همچنین به نظر می‌رسد نقش تابع دلتای کرونکر مشابه تابع نشانگر در اعداد صحیح باشد. در علوم مرتبط با سیگنال و پردازش آن، تابع دلتای کرونکر و تابع دلتای دیراک بسیار کاربرد دارند.