قانون اسنل — به زبان ساده

در این مقاله قصد داریم تا با زبانی ساده به معرفی و بررسی قانون اسنل (Snell's law) بپردازیم. به بیانی ساده، با استفاده از قانون اسنل می‌توانیم رفتار نور یا به طور کلی یک موج الکترومغناطیسی را در مرز بین دو محیط با ضریب شکست‌های مختلف، بررسی کنیم. به عبارت دیگر زاویه شکست و یا بازتاب نور در مرز مشترک دو محیط، توسط قانون اسنل تعیین می‌شود.

مقدمه

همان‌طور که در مقاله «طیف مرئی -- به زبان ساده» دیدیم، ناحیه فرکانسی محدودی از طیف الکترومغناطیسی که چشم انسان قادر به تشخیص آن است، طیف مرئی یا نور نامیده می‌شود. واژه «نور» (Optic) از این حیث به کار می‌رود که در علم فوتونیک به مجموعه سه ناحیه مادون قرمز (Infrared)، مرئی (Visible) و فرابنفش (Ultraviolet) ناحیه اپتیکی می‌گویند.

فیلم آموزش فیزیک پایه 3 – جامع و کاربردی در فرادرس

کلیک کنید

در واقع واژه «نور» معنایی فراتر از امواج قابل رویت توسط چشم انسان دارد.

با توجه به مطلب فوق، نور ماهیتی الکترومغناطیسی داشته و از میدان‌های الکتریکی و مغناطیسی عمود بر یکدیگر تشکیل شده است. در علوم اپتیک و فوتونیک، نور و همچنین برهمکنش‌های آن با ماده را توسط چهار دیدگاه‌ مختلف بررسی می‌کنند. این چهار دیدگاه در شکل زیر آمده‌اند.

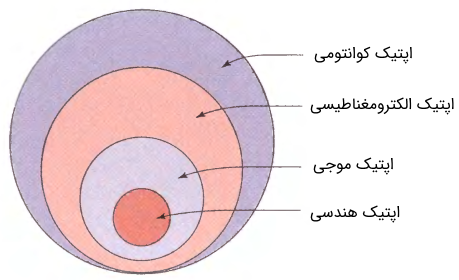
همان‌طور که در شکل فوق مشخص است، دیدگاه کوانتومی (Quantum Optics) از ۳ دیدگاه دیگر بالاتر قرار گرفته و جامع‌تر است. به عبارت دیگر تمامی پدیده‌های اپتیکی توسط این دیدگاه قابل تشریح و فرمول‌بندی هستند. دیدگاه سوم که شاید بیشترین کاربرد را در گرایش‌های نوری مهندسی برق الکترونیک و مخابرات دارد، دیدگاه الکترومغناطیسی (Electromagnetic Optics) است. در این دیدگاه، امواج یا فرکانس‌های اپتیکی (نور) همانند امواج رادیویی و مایکروویو (ریزموج) توسط معادلات ماکسول و شرایط مرزی در محیط‌های مختلف تحلیل و بررسی می‌شوند.

دیدگاه دوم که تقریب یا حد دیدگاه جامع‌تر الکترومغناطیسی است، دیدگاه موجی (Wave Optics) نام داشته که نور را به صورت جبهه‌های موج در نظر می‌گیرد. پدیده‌هایی نظیر تداخل و پراش که در دیدگاه محدود هندسی (Ray Optics) قابل بررسی و تشریح نیستند، در دیدگاه موجی به خوبی فرمول‌بندی می‌شوند. دیدگاه هندسی که ساده‌ترین مدل جهت بررسی رفتار نور است، نور را به صورت پرتو یا خط مستقیم درنظر می‌گیرد. بسیاری از تحلیل‌های ساده اپتیکی نظیر بررسی آینه‌‌ها (تخت، مقعر یا کاو، محدب یا کوژ) و عدسی‌ها (مقعر و محدب) توسط اپتیک هندسی صورت می‌گیرد.

در ادامه این مقاله، ما از دیدگاه اپتیک هندسی به بررسی دو پدیده بازتاب و شکست، توسط قانون اسنل می‌پردازیم. همچنین پدیده بازتاب داخلی که اساس کار انتقال نور یا سیگنال‌های اپتیکی در فیبرهای نوری است، بررسی می‌شود.

اپتیک هندسی

در اینجا نگاهی گذرا به اصل یا فرضیه‌های اپتیک هندسی خواهیم داشت. چرا که از این اصول در اثبات قانون اسنل استفاده می‌کنیم که در ادامه مقاله آمده است. گفتنی است که بررسی بیشتر این فرضیه‌ها خارج از حوصله این مقاله بوده و خود مقاله‌ای تخصصی‌تر را طلب می‌کند.

فیلم آموزش اپتیک یا نورشناسی Optique در فرادرس

کلیک کنید

• نور به صورت اشعه یا پرتو (Ray) و به صورتی خطی مستقیم منتشر می‌‌شود. پرتوهای نوری که آن را توسط خطوط نشان می‌دهیم از منابع نوری منتشر شده و توسط آشکارسازهای اپتیکی ثبت می‌شوند.
• محیط‌های مختلف توسط شاخصی اپتیکی به نام ضریب شکست (Refractive index) توصیف می‌شوند. ضریب شکست نسبت سرعت نور در خلأ به سرعت نور در محیط مذکور است.
• مدت زمانی که طول می‌کشد تا نور فاصله $$d$$ را طی کند، برابر با $$t = \frac{ d }{v} = \frac{ n d }{ c_{0} }$$ است. پارامتر $$nd$$ به طول مسیر اپتیکی (Optical path length) موسوم است. $$c_{0}$$ نیز سرعت نور در خلأ (ضریب شکست ۱) با مقدار $$3 \times 10^{ 8 }\ ( \frac{ m }{ s } )$$ است.
• محیط‌ ناهمگن (inhomogeneous)، محیطی است که در آن ضریب شکست تابعی از مختصات فضایی باشد، یعنی: $$\large n \equiv n ( r )$$
• در محیط‌های ناهمگن، طول مسیر اپتیکی بین دو نقطه $$A$$ و $$B$$ به صورت زیر محاسبه می‌شود ($$dl$$ دیفرانسیل طول است).

  $$\large Optical\ Pathlength\ =\ \int_{ A }^{ B } n ( r ) d l$$
  (1)

• اصل فرما (Fermat's Principle): دو نقطه $$A$$ و $$B$$ را در نظر بگیرید که با یکدیگر فاصله دارند. پرتوهای نوری برای رفتن از نقطه $$A$$ به نقطه $$B$$، مسیری را انتخاب می‌کنند که کمترین زمان یا کمترین طول مسیر اپتیکی را داشته باشد. به زبان ریاضی داریم:

  $$\large \delta \int_{ A }^{ B } n ( r ) d l = 0$$
  (2)

قانون اسنل

قانون اسنل به بیانی ساده، رابطه‌ای ریاضی است که ضریب شکست دو محیط را به واسطه دو زاویه برخورد (تابش) نور و زاویه شکست به یکدیگر مربوط می‌سازد.

$$\large n_{1} \sin \theta_{1} = n_{2} \sin \theta_{2}$$
(3)

فیلم آموزش فیزیک 3 – حل تمرین در فرادرس

کلیک کنید

در رابطه فوق، $$\theta_{ 1 }$$ زاویه تابش نور در محیط اول با ضریب شکست $$n_{ 1 }$$ و $$\theta_{ 2 }$$ زاویه شکست پرتو در محیط دوم با ضریب شکست $$n_{ 2 }$$ است. نکته بسیار مهمی که در این خصوص باید به آن توجه کنید، این است که ۳ پرتو تابش، بازتاب و شکست، هر ۳ در یک صفحه قرار دارند. صفحه مذکور به صفحه تابش یا برخورد موسوم است. سه پرتو مذکور در شکل زیر نشان داده شده‌اند. لازم به ذکر است که به پرتو شکست، پرتو عبور یافته (transmitted) نیز می‌گویند.

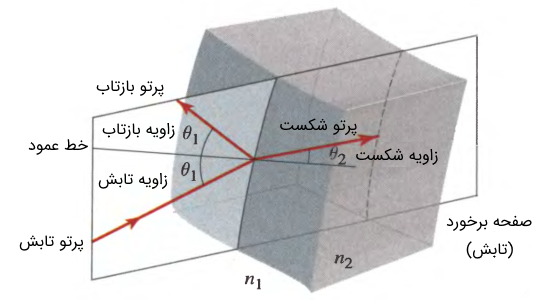
یکی از قوانین پایه اپتیک که از دوران مدرسه آن را به یاد دارید، این است که زاویه تابش و بازتابش با یکدیگر برابر هستند. زاویه بازتاب را غالباً به صورت پریم‌دار زاویه تابش نمایش می‌دهند. یعنی:

$$\large \theta_{1} = \theta_1^{'}$$
(4)

رابطه فوق از قانون اسنل نیز نتیجه می‌شود. از آنجایی که پرتو تابش و بازتابش هر دو در یک محیط (محیط با ضریب شکست $$n_{ 1 }$$) قرار دارند، داریم:

$$\large n_{1} = n_{2}\ \Rightarrow\ n_{1} \sin \theta_{1} = n_{1} \sin \theta_{2}\ \Rightarrow\ \theta_{1} = \theta_{2}$$
(5)

در رابطه فوق، $$\theta_{ 2 }$$ همان $$\theta_1^{'}$$ بوده و دقت داشته باشید تا آن را با زاویه شکست اشتباه نگیرید. به عبارت دیگر رابطه فوق در یک محیط با ضریب شکست $$n$$ نوشته شده است. در ادامه به بحث شکست پرتو می‌پردازیم. با توجه به قانون اسنل، بدیهی است که زاویه شکست به مقدار ضریب شکست دو محیط بستگی دارد. توجه داشته باشید که زاویه‌های تابش، بازتابش و شکست نسبت به خط عمود سنجیده می‌شوند (شکل 3).

$$\large n_{1} \sin \theta_{1} = n_{2} \sin \theta_{2}\ \Rightarrow\ \theta_{2} = \sin^{ -1 } (\frac{ n_{1} }{ n_{2} } \times \sin \theta_{1})$$
(6)

از رابطه فوق که فرمی از همان قانون اسنل است، می‌توان نتیجه گرفت که پرتو شکست بسته به مقدار ضریب شکست دو محیط، سه رفتار مطابق با شکل زیر دارد.

با توجه به شکل فوق، اگر ضریب شکست $$n_{ 2 }$$ بزرگ‌تر از ضریب شکست $$n_{ 1 }$$ باشد، پرتو شکست به سمت چپ خط فرضی امتداد پرتو تابش، شکسته شده یا به اصطلاح خم می‌شود یا به عبارت دیگر به خط عمود نزدیک می‌شود. در واقع زاویه شکست $$\theta_{ 2 }$$ کوچکتر از زاویه تابش $$\theta_{ 1 }$$ می‌شود. این امر به شکست خارجی نیز موسوم است.

همچنین اگر $$n_{ 2 }$$ کوچک‌تر از $$n_{ 1 }$$ باشد، پرتو شکست به سمت راست خط فرضی امتداد پرتو تابش خم می‌شود یا به عبارتی از خط عمود دور می‌شود. این امر به این معنی است که زاویه شکست $$\theta_{ 2 }$$ بزرگتر از زاویه تابش $$\theta_{ 1 }$$ می‌شود. این امر به شکست داخلی نیز موسوم است. بدیهی است که اگر $$n_{ 1 } = n_{ 2 }$$ باشد، نور بدون شکست به مسیر خود ادامه داده و سهمی از آن با زاویه‌ای برابر با زاویه تابش ($$\large \theta_{1} = \theta_1^{'}$$)، بازتاب می‌شود.

با به کارگیری قانون اسنل در مرز مشترک هوا (ضریب شکست یک) و ماده‌‌ای خاص (البته شفاف) می‌توانیم به صورت زیر، ضریب شکست ماده مذکور را به دست آوریم:

$$\large n_{1} \sin \theta_{1} = n_{2} \sin \theta_{2}\ \ , \ n_{1} = 1\ \rightarrow\ n \equiv n_{2} = \frac{ \sin \theta_{1} }{ \sin \theta_{2} }$$
(7)

مثال

فرض کنید که نور قرمز رنگ حاصل از یک دیود لیزری با زاویه ۵۳ درجه به سطح آب برخورد کرده و در زاویه ۳۷ درجه دچار شکست شده و به آب وارد می‌شود. ضریب شکست آب را می‌توانیم به صورت زیر محاسبه کنیم:

$$\large n_{water} = \frac{ \sin 53^\circ }{ \sin 37^\circ } = 1.33$$
(8)

همان‌طور که بیان کردیم، پدیده شکست ارتباط مستقیمی به ضریب شکست محیط دارد. با توجه به تعریف ضریب شکست، می‌توان تفاوت سرعت نور در دو محیط مختلف را عامل شکست نور یا به طور کلی شکست امواج الکترومغناطیسی دانست. ضریب شکست یک محیط، نسبت سرعت نور در خلأ به سرعت نور در آن محیط تعریف می‌شود.

$$\large n = \frac{ c }{ v } = \frac { 3 \times 10^{8}\ (\frac{ m }{ s })}{ v }$$
(9)

با توجه به رابطه فوق، قانون اسنل را می‌توان برحسب سرعت نور در دو محیط نیز به صورت زیر نوشت:

$$\large n = \frac{ c }{ v }\ \Rightarrow\ v_{2} \sin \theta_{1} = v_{1} \sin \theta_{2}$$
(10)

رابطه (9)، تعریفی بسیار ساده از پارامتر ضریب شکست است. دیدگاه نظریه الکترومغناطیس در خصوص ضریب شکست کامل‌تر از رابطه فوق است. در مقاله «امپدانس ذاتی محیط — به زبان ساده» دیدیم که ضریب شکست یک محیط تابعی از ویژگی‌های بنیادی محیط نظیر نفوذپذیری الکتریکی و نفوذپذیری مغناطیسی است. لازم به ذکر است که ضریب شکست در حالت کلی عددی مختلط بوده که قسمت موهومی آن تابعی از فرکانس یا طول موج است. در نتیجه ضریب شکست مواد مختلف برای قسمت‌های مختلف طیف الکترومغناطیسی ( فرکانس‌های مختلف) می‌تواند متفاوت باشد.

$$\large n = \sqrt{ \frac{ \epsilon \mu }{ \epsilon_{0} \mu_{0}} }$$
(11)

در جدول زیر ضریب شکست مواد مختلفی حاصل از سدیم در طول موج $$589nm$$ آمده است.

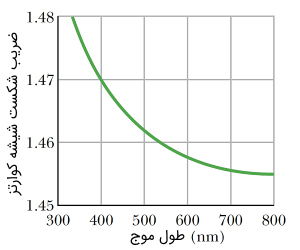
از مطلب فوق نتیجه می‌شود که زاویه شکست برای نور با فرکانس‌ یا طول موج‌های مختلف متفاوت است. دلیل اینکه نور قرمز (طول موج بیشتر) و نور آبی (طول موج کمتر) در زوایای مختلفی به هنگام خارج شدن از منشور دچار شکست می‌شوند، همین امر است. به عبارت دیگر، دلیل پاشندگی نور در یک منشور این است که ضریب شکست منشور برای طول موج‌های مختلف از نور سفید که به آن برخورد می‌کند، متفاوت است.

اثبات قانون اسنل

اثبات رابطه ریاضی قانون اسنل در اپتیک هندسی با استفاده از قانون یا اصل فرما (Fermat's Principle) و با توجه به شکل (7) به صورت زیر انجام می‌شود.

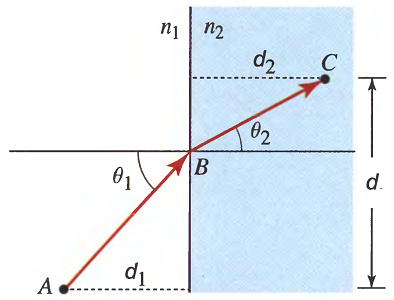
همان‌طور که پیش‌تر بیان کردیم، اصل فرما بیان می‌کند، مسیری که پرتو نوری بین دو نقطه طی می‌کند، کوتاه‌ترین مسیر ممکن چه از لحاظ زمانی و چه از لحاظ مکانی است. با توجه به شکل فوق، قانون یا اصل فرما را برای مسیر $$AC$$ به شکل زیر می‌نویسیم:

$$\large \delta \int_{ A }^{ C } n ( r ) d l = 0$$

$$\large \int_{ A }^{ C } n ( r ) d s = \int_{ A }^{ B } n ( r ) d l + \int_{ B }^{ C } n ( r ) d l$$
(12)

با توجه به مثلث‌های قائم‌الزاویه‌ای که می‌توانند در شکل فوق تشکیل شوند، جزء دیفرانسیلی طول $$d l$$ را برای دو انتگرال فوق، از رابطه فیثاغورث به دست می‌آوریم:

$$\large \int_{ A }^{ C } n ( r ) d s = \int_{ A }^{ B } n ( r ) d s + \int_{ B }^{ C } n ( r ) d s = n_{ 1 } \sqrt{ r_{ 1 }^{ 2 } + d_{ 1 }^{ 2 } } + n_{ 2 } \sqrt{ ( d - r_{ 1 })^{ 2 } + d_{ 2 }^{ 2 } }$$
(13)

$$\large \delta\ \rightarrow\ \frac{ \partial }{ \partial r }\ \Rightarrow\ \int_{ A }^{ C } n ( r ) d s = n_{ 1 } \sqrt{ r_{ 1 }^{ 2 } + d_{ 1 }^{ 2 } } + n_{ 2 } \sqrt{ ( d - r_{ 1 })^{ 2 } + d_{ 2 }^{ 2 } } = 0$$
(14)

$$\large \Rightarrow \frac{ \partial }{ \partial r } ( n_{ 1 } \sqrt{ r_{ 1 }^{ 2 } + d_{ 1 }^{ 2 } } + n_{ 2 } \sqrt{ ( d - r_{ 1 })^{ 2 } + d_{ 2 }^{ 2 } } ) = \frac{ n_{ 1 } r_{ 1 } }{ \sqrt{ r_{ 1 }^{ 2 } + d_{ 1 }^{ 2 } } } - \frac{ n_{ 2 } ( d - r_{ 1 } ) }{ \sqrt{ ( d - r_{ 1 } )^{ 2 } + d_{ 2 }^{ 2 } } } = 0$$
(15)

$$\large \Rightarrow \frac{ n_{ 1 } r_{ 1 } }{ \sqrt{ r_{ 1 }^{ 2 } + d_{ 1 }^{ 2 } } } = \frac{ n_{ 2 } ( d - r_{ 1 } ) }{ \sqrt{ ( d - r_{ 1 } )^{ 2 } + d_{ 2 }^{ 2 } } }$$
(16)

با توجه به رابطه سینوس زاویه در مثلث‌های قائم‌الزاویه تشکیل شده داریم:

$$\large \Rightarrow n_{ 1 } \sin \theta_{ 1 } = n_{ 2 } \sin \theta_{ 2 }$$
(17)

بازتاب داخلی کلی

یکی از مهم‌ترین پدیده‌هایی که در مرز مشترک دو محیط با ضریب شکست مختلف می‌تواند رخ دهد، پدیده بازتاب داخلی کلی است. پدیده مذکور اساس کار ساختارهای موجبری (Waveguide) نظیر فیبر نوری است.

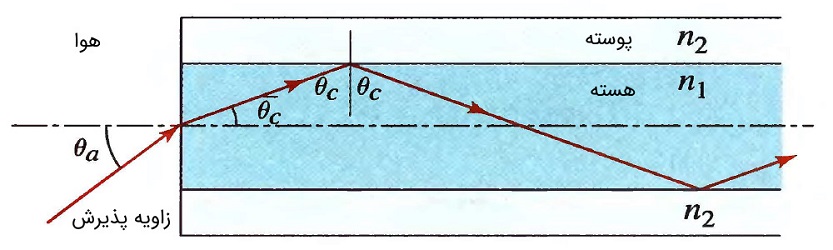
پیش‌تر بیان کردیم که زاویه‌های شکست و تابش نسبت به خط عمود سنجیده می‌شوند. با توجه به شکل (9) بیشترین زاویه‌ای که پرتو شکست نسبت به خط عمود می‌تواند داشته باشد، 90 درجه است. پس با توجه به قانون اسنل داریم:

$$\large n_{1} \sin \theta_{1} = n_{2} \sin \theta_{2}\ \ , \ \theta_{2} = 90^\circ\ \rightarrow\ \theta_{c} \equiv \theta_{1} = \sin^{-1} (\frac{ n_{2} }{ n_{1} })$$

زاویه $$\theta_{ c }$$ به زاویه حد موسوم است. زاویه حد $$\theta_{ c }$$، زاویه‌ای است که در آن پرتو شکست به اندازه 90 درجه خم شده و روی مرز دو محیط حرکت می‌کند. حال اگر پرتو تابش با زاویه‌ای بیشتر از زاویه حد به مرز بین دو محیط با ضریب شکست $$n_{ 1 }$$ و $$n_{ 2 }$$ بتابد، پرتو به طول کامل بازتاب پیدا می‌کند. همان‌طور که می‌دانیم، زاویه بازتاب با زاویه تابش برابر است. شکل زیر رفتار نور تابشی با زوایای مختلف را در مرز دو محیط با ضریب شکست‌های متفاوت (شیشه و هوا) نشان می‌دهد.

دقت داشته باشید برای آنکه پدیده بازتاب کلی رخ دهد، ضریب شکست محیط اولیه‌ای که نور از آن می‌گذرد باید بیشتر از ضریب شکست محیط ثانویه‌ای باشد که با آن مرز مشترک دارد. به طور مثال، در فیبرهای نوری، ضریب شکست هسته (Core) بیشتر از ضریب شکست پوسته (Clade) است.

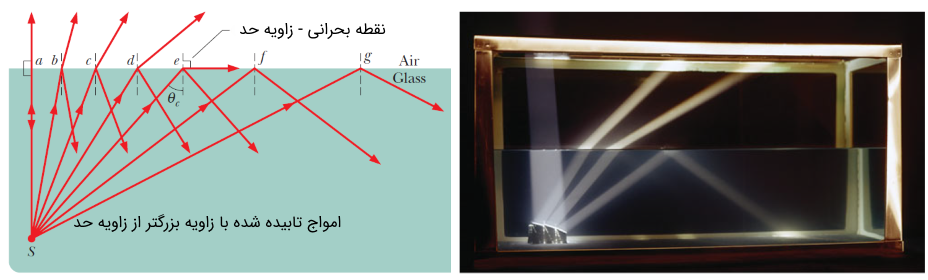
برای حالت خاصی که محیط $$n_{ 2 }$$ هوا باشد، زاویه حد به صورت زیر در می‌آید. به عبارت دیگر می‌توان در جسمی با ضریب شکست بیشتر از یک، نور را با زاویه تابش بیشتر از حد ($$\theta_{ i } > \theta_{ c }$$) به دام انداخت.

$$\large \theta_{c} = \sin^{-1} (\frac{ n_{2} }{ n_{1} })\ \ ,\ \ n_{2,air} = 1 \Rightarrow\ \theta_{c} = \sin^{-1} (\frac{ 1 }{ n_{1} })$$

اگر این مطلب برای شما مفید بوده است، آموزش‌های زیر را نیز به شما پیشنهاد می‌کنیم:

• لیزر چیست؟ -- به زبان ساده
• میزر (Maser) -- به زبان ساده
• مخابرات فیبر نوری -- راهنمای جامع
• FTTH چیست؟ -- از صفر تا صد

^^