ضریب جینی چیست؟ – به زبان ساده
در این مطلب به بررسی ضریب جینی (Gini Coefficient) میپردازیم که یکی از شاخصهای برجسته اندازهگیری نابرابری در توزیع ثروت و درآمد است. با اینکه اقتصاد در بیشتر زمانها بر تخصیص بهینه منابع تمرکز داشته است اما از اهمیت نحوه توزیع درآمد و ثروت برای سیاستگذاران نیز نباید غافل شد.


کشورهایی که نابرابری زیادی را در توزیع درآمد و ثروت تجربه میکنند، در برابر اغتشاشهای اجتماعی و بیثباتی سیاسی آسیبپذیرتر هستند زیرا نگرانی درباره عدالت و برابری، بر دیدگاه ما راجع به احزاب مختلف سیاسی و سیاستهای بازتوزیع، اثر میگذارد. به صورت کلی ضریب جینی بررسی میکند که چه درصدی از کل درآمد یا ثروت به چه سهمی از جمعیت تعلق گرفته است.
تعریف شاخص جینی
ضریب جینی یا «شاخص جینی» (Gini index) معیار اندازهگیری توزیع درآمد (یا ثروت) در یک جمعیت است که اولینبار توسط آماردان ایتالیایی «کورادو جینی» (Corrado Gini) در سال ۱۹۱۲ میلادی بوجود آمده است. این ضریب همچنان جزو یکی از شناختهشدهترین شاخصهای نابرابری در بین بیش از ۵۰ شاخص به شمار میآید.
به طورمعمول، از این شاخص برای سنجش نابرابری اقتصادی استفاده میشود. این شاخص توزیعدرآمد یا به عبارتی توزیع ثروت در میان یک جمعیت را بررسی میکند. ضریب جینی اعدادی بین صفر تا ۱ را به خود میگیرد که صفر ( یا ۰٪) نشاندهنده برابری کامل و ۱ (یا ۱۰۰٪) نشاندهنده نابرابری مطلق است. طبق داده های بانک جهانی، بین سالهای ۱۹۸۱ تا ۲۰۱۳ میلادی، ضریب جینی بصورت جهانی بین ۰/۳ تا ۰/۶ بوده است.
این امکان وجود دارد که از لحاظ نظری، شاخص جینی بیشتر از ۱ باشد که بیانگر درآمد یا ثروت منفی یا زیرصفر است. شاخص یا ضریب جینی از منحنی لورنز برگرفته شده است. هر چه مقدار محاسبه شده ضریب جینی برای کشوری بیشتر باشد، نشاندهنده نابرابری بیشتر در توزیع درآمد آن کشور است.
هنگامی که شاخص جینی بسیار بالا و نزدیک به عدد ۱ باشد، این مطلب دریافت میشود که افراد با درآمد بالا، به صورت نامتناسبی، حجم زیادی از کل درآمد را دریافت میکنند. از شاخص جینی نه تنها در علوم اجتماعی و اقتصاد بلکه در علوم زیستی ، شیمی و فیزیک (مانند بررسی جینتروپی: کلیتبخشی به آنتروپی برپایه شاخص جینی)، ریاضیات و حتی کامپیوتر و دادهکاوی نیز بهره گرفته میشود. برای مثال یکی کاربردهای شاخص جینی، در مباحث درخت تصمیمگیری است.
منحنی لورنز و ضریب جینی
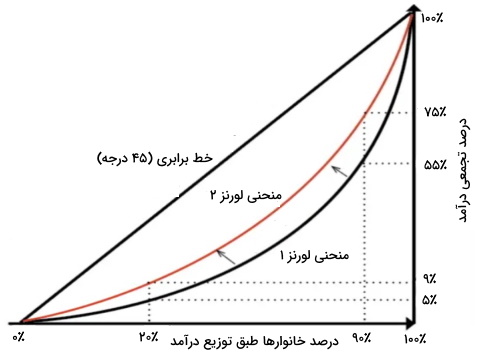
شاخص جینی بصورت ریاضی بر پایه منحنی لورنز تعریف میشود. منحنی لورنز اولین بار توسط «ماکس لورنز» (Max O.Lorenz) در سال ۱۹۰۵ میلادی برای تشریح چگونگی توزیع ثروت بوجود آمد. منحنی لورنز در دستگاه مختصات دکارتی و با دو محور به نمایش درمیآید. در منحنی لورنز، محور افقی یا همان محور ، نشاندهنده درصد تجمعی خانوارها یا افرادی است که دریافت کننده درآمد هستند. مبدا این محور از کمترین درآمد شروع میشود و به بیشترین درآمد میرسد.
محور عمودی یا محور ، بیانگر درصد درآمد تجمعی یا ثروت تعلق گرفته است. بنابراین، نقطه (۰/۰۵، ۰/۲) در منحنی زیر به ما نشان میدهد ۲۰ درصدی از جمعیت که کمترین درآمد به آنها تعلق گرفته است، تنها ۵ درصد از کل درآمد را بدست آوردهاند.
در جامعهای که برابری مطلق داریم، منحنی لورنز به شکلی خواهد بود که محور با محور برابر باشد. به عقیده بعضی از اقتصاددانان، ضریب جینی کاربردی و مفید است زیرا مقادیر منفی درآمد و ثروت را برعکس بعضی معیارهای اندازهگیری نابرابری دیگر، در نظر میگیرد.
برای مثال، اگر بخشی از جمعیت ثروت منفی یا بدهی داشته باشد، منحنی لورنز به سمت پایین محور خواهد رفت. در تصویر زیر، ۲۰ درصد از فقیرترین افراد جامعه، تنها ۵ درصد از درآمد کل را دریافت میکنند. در این تصویر همچنین، ۹۰ درصد فقیر جمعیت، دریافتکننده ۵۵ درصد کل درآمد هستند بدین معنی که به ۱۰ درصد ثروتمند، ۴۵ درصد از کل درآمد تعلق میگیرد.

انتقال در منحنی لورنز
در شکل زیر، منحنی لورنز قبل از انتقال را با شماره ۱ و منحنی لورنز پس از انتقال را با شماره ۲ مشخص کردهایم. همانطور که مشاهده میکنید، نابرابری کاهش یافته است و شاهد کاهش فاصله منحنی لورنز ۱ از خط برابری هستیم و حال، منحنی لورنز ۲ بوجود آمده است. در منحنی لورنز شماره ۲، ۲۰ درصد فقیر جمعیت، ۹ درصد درآمد را کسب میکنند. پس از انتقال منحنی لورنز، ۲۵ درصد درآمد کل، به ۱۰ درصد متمول جامعه میرسد. آنها قبل از انتقال منحنی، ۴۵ درصد از درآمد کل را دریافت میکردند. در نتیجه، نابرابری در توزیع درآمد کاهش یافته است.
نحوه عملکرد شاخص جینی
فرض کنید کشوری داریم که همه شهروندان آن درآمد یکسانی دریافت میکنند. در این کشور ضریب جینی برابر صفر خواهد بود. حال فرض کنید کشوری داریم که در آن تمام درآمد نصیب یک شهروند شده است و باقی شهروندان درآمدی دریافت نکردهاند. شاخص جینی محاسبه شده برای این کشور، برابر با یک خواهد بود.
تحلیل بالا را میتوانیم برای شاخص ثروت جینی نیز بکار ببریم با این تفاوت که چون اندازهگیری ثروت دشوارتر است، هنگام به کاربردن ضریب جینی از درآمد استفاده میکنیم. به صورت عمومی، شاخص ثروت جینی بزرگتر از شاخص درآمدیِ آن خواهد بود زیرا نابرابری بیشتری در توزیع ثروت داریم. البته، یک کشور کمدرآمد و یک کشور پردرآمد ممکن است شاخص جینی برابری داشته باشند. این حالت تا زمانی برقرار است که درآمد در هریک از این کشورها بصورت مشابهی توزیع شده باشد.
برای فهم بهتر مطلب، به این مثال توجه کنید. در سال ۲۰۱۶ میلادی شاخص جینی در ترکیه و آمریکا (طبق آمار منتشر شده از سازمان همکاری و توسعه اقتصادی) حدود 0/39-0/40 بوده است. با اینحال جی دی پی سرانه ترکیه (برپایه قیمتهای سال ۲۰۱۰ و برحسب دلار آمریکا) کمتر از نصف GDP سرانه آمریکا بوده است. بانک جهانی جزو معدود ارگانهایی به شمار میآید که دادههای مربوط به شاخص جینی را منتشر میکرده است اما در حال حاضر چنین کاری صورت نمیگیرد و هنگام ارائه اطلاعات تنها به سهم درآمدی ۲۰ درصد فقیر، اشاره میکند.
فرمول ضریب جینی
شاخص یا ضریب جینی بصورت کلی نابرابری را در میان مقادیر مختلف یک متغیر اندازهگیری میکند. هرچه این شاخص بالاتر باشد، دادهها پراکندهتر هستند. به عبارت دیگر، شاخص جینی از تقسیم مساحت بین خط برابری و منحنی لورنز بر کل مساحت قرار گرفته زیر خط برابری محاسبه میشود.
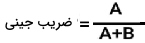
در مقایسه شاخص جینی باید توجه کرد که در محاسبه این ضریب، بعضی کشورها از آمار قبل از کسر مالیات و بعضی از کشورها از آمار بعد از کسر مالیات استفاده میکنند. بصورت طبیعی، وقتی از آمار بعد از کسر مالیات بهره میگیریم، ضریب جینی کمی کاهش مییابد زیرا توزیع درآمد از ثروتمندان به فقیران صورت گرفته است و در نتیجه، نابرابری کمتری داریم.
مثال محاسبه ضریب جینی
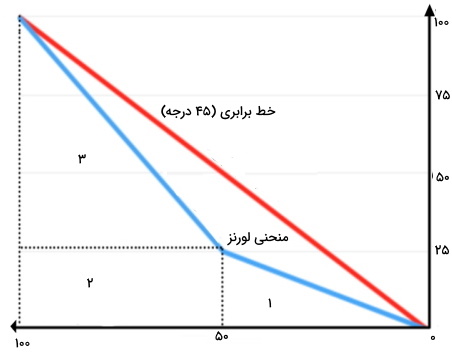
برای درک بهتر نحوه محاسبه ضریب جینی به این مثال توجه کنید. در تصویر زیر ما باید ابتدا مساحت ناحیه B (زیر منحنی لورنز) را حساب کنیم. میتوانیم این کار را با تقسیم کردن این بخش به مثلثها و مربعهای متفاوت انجام دهیم. در شکل زیر، مساحت زیر منحنی آبی به سه بخش تقسیم میشود.
قاعده × ارتفاع × 0/5 = مساحت مثلث
625 = 50 × 25 × 0/5 = مساحت ناحیه ۱
1875 = ۵۰ × ۷۵ × 0/5 = مساحت ناحیه ۳
طول × عرض = مساحت مستطیل
1250 = ۵۰ × ۲۵ = مساحت ناحیه ۲
در نتیجه، کل مساحت ناحیه B برابر با مجموع مساحت این ۳ ناحیه خواهد بود.
3750 = 1250 + 1875 + 625
مساحت قسمتی از نمودار که زیر خط برابری قرار گرفته است معادل ۱۰۰*۱۰۰*۰/۵ خواهد بود. در نتیجه، مساحت کل نمودار شامل هر دو بخش A و B، برابر ۵۰۰۰ خواهد بود. مساحت ناحیه A از کسر مساحت ناحیه B از مساحت کل بدست میاید. مساحت ناحیه A برابر است با:
1250 = 3750 - 5000
حال میتوانیم این مقادیر را در فرمول محاسبه ضریب جینی قرار دهیم:
0/25 = (۳۷۵۰+۱۲۵۰)/۱۲۵۰ = ضریب جینی
ضریب جینی کشورهای مختلف
حال که ما نحوه محاسبه ضریب جینی را میدانیم بهتر است، به مقایسه ضرایب جینی در کشورهای مختلف بپردازیم که ببینیم در هر زمان چه مقداری به خود اختصاص داده است. بدین شکل میتوانیم تغییرات بوجودآمده در نابرابری را نیز مشاهده کنیم. جدول زیر حاوی ضریب Gini برای ۵ کشور در دو سال ۲۰۰۰ و ۲۰۱۶ میلادی است. هر یک از کشورهای انتخاب شده ضریب جینی بین ۰/۲۷ و ۰/۵۳ دارند. شاخص جینی ۰/۵۳، عدد بالایی در نظر گرفته میشود و حاکی از آن است که درآمد، بیشتر از اینکه به صورت برابر توزیع شده باشد، به صورت نابرابر توزیع شده است، برای مثال میتوانیم به مکزیک اشاره کنیم.
ضریب جینی حدود ۰/۲۸ در نروژ بیانگر این است که درآمد در راستای ایجاد برابری در این کشور، البته نه بصورت مطلق و تساویگرایانه توزیع شده است. در بین ۵ کشوری که در جدول زیر داریم، نابرابری درآمدی در مکزیک پس از آمریکا از همه بالاتر است و نروژ کمترین ضریب جینی را داشته است. در ۳ کشور از ۵ کشور (آلمان، آمریکا و نروژ) ضریب جینی بین سالهای ۲۰۰۰ تا ۲۰۱۶ افزایش و در مکزیک کاهش یافته است.
| کشورها | ضریب جینی در سال ۲۰۰۰ | ضریب جینی در سال ۲۰۱۶ |
| آلمان | 0/29 | 0/32 |
| ایالات متحده آمریکا | 0/4 | 0/41 |
| مکزیک | 0/53 | 0/46 |
| ایتالیا | 0/35 | 0/35 |
| نروژ | 0/27 | 0/29 |
نقاط ضعف شاخص جینی
ضریب جینی کاستیهایی دارد. برای مثال، تمام دادههای منحنی لورنز را به عنوان ورودی دریافت میکند و تنها یک عدد را به عنوان خروجی تحویل میدهد. همانطور که در بالا دیدیم، دو کشور با توزیع درآمد متفاوت میتوانند ضریب جینی یکسانی داشته باشند.
در ادامه، از جنبههای گوناگون، محدودیتهای ضریب Gini را مورد توجه قرار خواهیم داد:
- فرض کنید که فرد الف ۲۴ ساله و دانشجوی پزشکی است و بخاطر وامهای دانشجویی درآمد منفی دارد (مقروض است). حال، فرد ب را تصور کنید که به همان اندازه فرد الف درآمد منفی دارد ولی بیکار است و آینده شغلی ندارد. شاخص جینی از آدمها در برهه زمانی تصادفی از زندگیشان نمونهگیری میکند. یعنی، نمیتواند بین افرادی از جامعه که آینده مالیشان بصورت معقولانهای تامین شده است و آنهایی که آینده شغلی ندارند، تفاوت قائل شود.
- نتایج شاخص جینی به شدت تحت تاثیر دادههای پرت قرار میگیرد. عده اندکی که بسیار ثروتمند یا بسیار فقیر هستند میتوانند حتی در یک جامعه آماری بزرگ نتیجه را تا حد قابلتوجهی تغییر دهند.
- یکی دیگر از کاستیهای شاخص جینی، برداشت متفاوت از مفهوم درآمد است. درآمد میتواند در سطح خانوار تعریف شود و مقدار آن نسبت به اندازه خانوار یا دیگر مقیاسها تغییر کند یا در سطح فردی تعریف شود و داراییهای مالی یا دستمزد بدست آمده را مورد توجه قرار دهد.
هر تعریفی که از درآمد داشته باشیم، معیار ما برای اندازهگیری آن، متفاوت خواهد بود و بسته به تعریف مدنظرمان، سطح نابرابری درآمدی متفاوت خواهد بود. بنابراین، در محاسبه شاخص Gini رتبه کشورها بسته به در نظر گرفتن نوع درآمد خانوار یا درآمد فردی تغییر می کند. - در اقتصادهایی که بر پایه کشاورزی و معیشتی هستند، ممکن است درآمد غیرپولی هم داشته باشیم. کشورها نیز نظامهای مالیاتی متفاوتی دارند. هر روش جمعآوری مالیات اعم از مالیات تصاعدی (هنگامی که مبلغ مالیاتپذیر افزایش پیدا میکند، این مالیات هم افزایش مییابد)، مالیاتهای تنازلی (عکس روش تصاعدی) و مالیات تعادلی (حد میانگین روشهای تصاعدی و تنازلی است) ممکن است نتایج متفاوتی را در هر کشور داشته باشند و هر نظام مالیاتی ممکن است بازتوزیعکنندهتر از سایر نظامهای مالیاتی به شمار آید.
- ضریب جینی ممکن است یک شاخص اندازهگیری نسبی باشد و تفاوتهای مطلق درآمدی را ثبت نکند. این امکان وجود دارد که ضریب جینی یک کشور به علت افزایش نابرابری درآمدی زیاد شود و در همین زمان تعداد افرادی که در فقر مطلق زندگی میکنند، کاهش یابد. علت آن است که شاخص Gini اصل بهبود پارتو را نقض میکند. اصل بهبود پارتو بیان میکند که اگر در یک جامعه مفروض همه درآمدها افزایش پیدا کند، نابرابری درآمدی میتواند افزایش یابد.
- ضریب جینی نمیتواند منافع اجتماعی یا دیگر موارد تاثیرگذار در نابرابری بین قشر مرفه و فقیر را ثبت کند. خدمات درمانی و تحصیلات با کمک یارانه و کمک هزینههای اجتماعی برای قشر آسیببپذیر، مواردی هستند که به خانوارها در بهبود وضعیت معیشتیشان کمک میکنند و از نابرابری درآمدی میکاهند.
- تغییر در جمعیت و ویژگیهای آن بوسیله شاخص جینی منعکس نمیشود. در کشورهایی که درصد بالایی از جمعیتشان را سالمندان تشکیل میدهند که عمده درآمدشان از حقوق بازنشستگی است یا کشورهایی که تعداد زیادی دانشجو دارند این احتمال میرود که نابرابری درآمدی اندازهگیری شده توسط که توسط ضریب Gini، بالاتر باشد.

معرفی فیلم آموزش آشنایی با اقتصاد بخش عمومی ۲
برای آشنایی بیشتر با مفهوم ضریب جینی و سایر مباحث پیرامون اقتصاد رفاه و توزیع درآمد میتوانید به آموزش بالا مراجعه کنید. این آموزش ویدئویی توسط فرادرس و در قالب دورهای ۳ساعته و در ۶ درس تدوین شده است. در آموزش حاضر در درس اول به تعریف اقتصاد بخش عمومی پرداخته میشود. در درس دوم، وظایف اقتصاد بخش عمومی شرح داده شده است. درس سوم و درس چهارم به ترتیب موضوعات مرتبط با پیامد خارجی و دلایل دخالت دولت در اقتصاد میپردازد. تعاریف مربوط به کالای عمومی در درس هفتم شرح داده شده است.
- برای مشاهده فیلم آموزش آشنایی با اقتصاد بخش عمومی ۲ + اینجا کلیک کنید.
جمع بندی
ضریب جینی نباید به عنوان تنها معیار اندازهگیری نابرابری اقتصادی مورد استفاده قرار بگیرد. میتوانیم به شاخص جینی تنها به عنوان یک داده آماری نگاه یا از آن استفاده کنیم تا به قسمت بالای توزیع توجه داشته باشیم و به تصویر واضحتری برسیم.
به خاطر محدودیت دادهها، شاخص جینی میتواند تمرکز ثروت را در افراد خیلی ثروتمند، کمتر از حد واقعیاش نشان دهد. این ضریب حتی میتواند نابرابری ثروتی را در ردههای بالاتر ثروتمندان کمتر از حد واقعی نمایش دهد. برای کم کردن این اثر ، به عقیده «فرانک کاول» (Frank Cowel) ، استاد دانشگاه اقتصاد لندن، میتوان از روشهای بهتری برای مدلسازی توزیع درآمد و ثروت برای قشر مرفه استفاده کرد. یک راه این است که توزیعی احتمالی (به طور بخصوص توزیع پارتو) را برای ۵ یا ۱۰ درصد متمول جامعه بکار ببریم.
ممکن است این سوال بوجود بیاید که نابرابری در یک جامعه به چه صورت است. به عقیده کاول، تمرکز ثروت در دسته بالاییِ جمعیت میتواند گویای این باشد که در کسبوکار، انحصار وجود دارد. در محاسبه ضریب جینی در توزیع نابرابری باید به تفاوت بین ثروت و درآمد توجه کنیم.
نابرابری در ثروت بیشتر نشاندهنده نحوه توزیع قدرت در یک جامعه است و نابرابری در درآمد به ما نشانمیدهد که بازار کار چگونه عمل میکند. اگر به اندازهگیری نابرابری علاقهمند هستید ممکن است بخواهید از معیارهای دیگری مانند «شاخص هوور» (Hoover-index) و «شاخص تیل» (Theil-index) استفاده کنید. البته باید به این توجه کنیم که هیچ معیاری نمیتواند تمام ویژگیهای مورد نظر ما را داشته باشد و ترجیح معیار اندازهگیری به معیاری دیگر، اغلب با صرفنظر از بعضی موارد، همراه است. شاید برای بدست آوردن تحلیلی همهجانبه و متوازن از نابرابری، به بررسی همزمان چندین شاخص با یکدیگر نیاز داشته باشیم.













با سلام،
ممنون بخاطر توضیحاتتون
میخواستم بدونم ضریب جینی ایران چقدر هست؟
با سلام خدمت شما؛
براساس آمار رسمی ضریب جینی درآمد خانوارهای ایرانی در سال ۱۴۰۲ برابر با ۰٫۳۹۷۹ گزارش شده است. همچنین در سال ۱۴۰۳ نیز گزارش مرکز آمار ایران عدد ۰٫۳۸۷۰ را اعلام کرده است.
از همراهی شما با مجله فرادرس سپاسگزاریم.
درود بر شما، بسیار ساده و روان بود.
با سلام و احترام
درود بر شما بسیار عالی بود
سلام. با تشکر، استفاده کردم.
سلام ، عالی بود ، استفاده کردم .
درود و عرض ادب عالی بود و آموزنده
عالی بود
با سپاس از شما
ممنون
مفید بود