فرادرسسطح شیبدار چیست؟ — به زبان ساده
احتمالا تجربه سفر در جاده‌های کوهستانی را داشته‌اید. شاید این سوال در ذهن شما شکل گرفته باشد که چرا در پیچ‌ها، در اکثر موارد جاده‌ها به صورت شیبدار طراحی می‌شوند. در این مطلب قصد داریم تا در مورد سطح شیبدار صحبت کرده و توضیح دهیم که چگونه این سطوح منجر به عدم انحراف خودرو در هنگام دور زدن می‌شود.
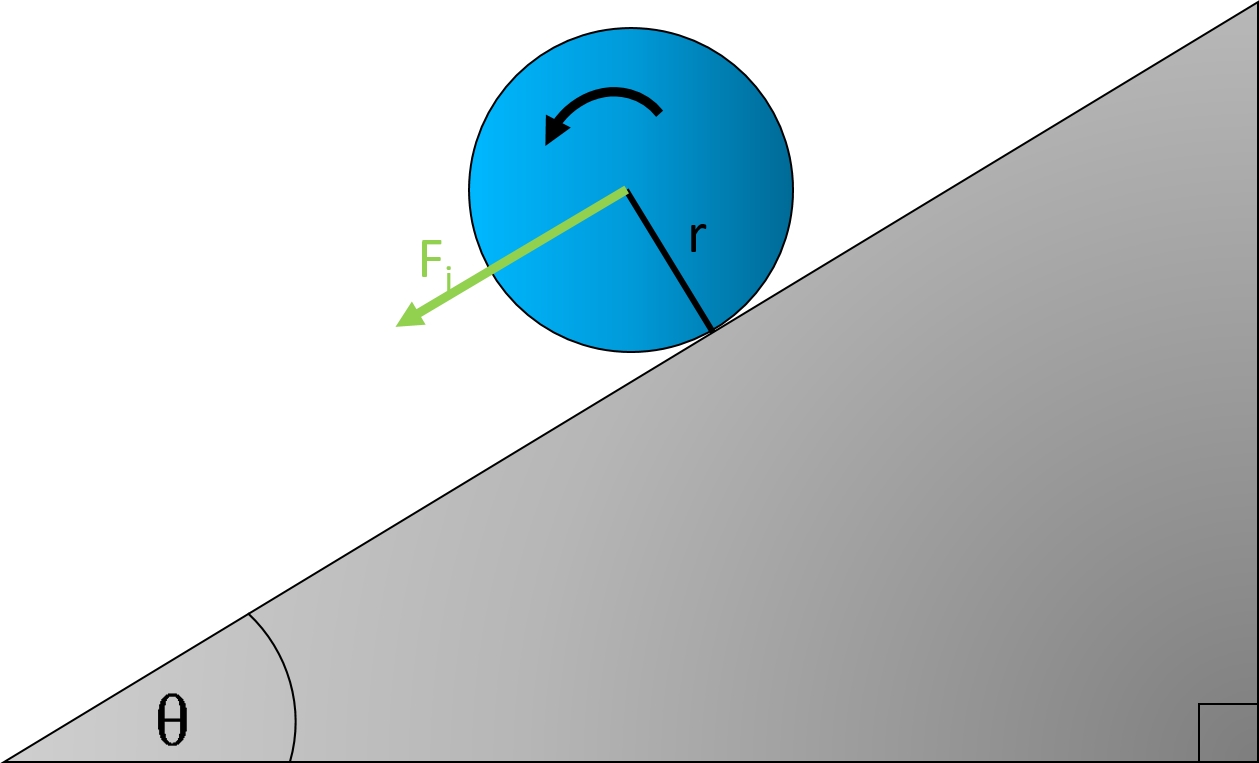
به منظور درک بهتر، پیشنهاد می‌شود قبل از مطالعه، مطالب قوانین حرکت نیوتن، اصطکاک، بردار و حرکت دایره‌ای را مطالعه فرمایید.
مقدمه
به منظور بررسی نحوه حرکت یک جسم روی سطح شیبدار در ابتدا مطابق با شکل زیر سطحی شیبدار با زاویه $$θ$$ را در نظر بگیرید که روی آن جرمِ $$m$$ قرار گرفته است.
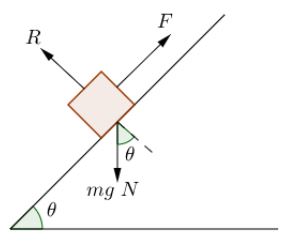
فرض کنید سطح دارای اصطکاک نباشد. در این صورت جرم $$m$$ با شتاب ثابتی به سمت پایین حرکت خواهد کرد. به منظور حل چنین سیستمی در ابتدا باید دستگاه مختصات مناسب در نظر گرفته شود. در نتیجه برای راحتی کار محور $$y$$ها را در جهت $$R$$ و محور $$x$$ها را در جهت $$F$$ در نظر می‌گیریم.
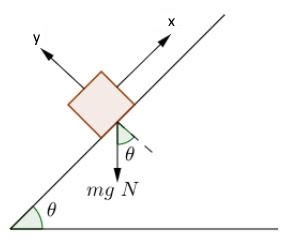
نیروهای وارد شده به سیستم شامل نیروی $$F$$ و نیروی وزن می‌شوند. پس از شناسایی نیروها باید قانون دوم نیوتن را در دو راستای $$x$$ و $$y$$ برای جرم $$m$$ نوشت. به منظور نوشتن تعادل نیرویی، توجه به دو نکته ضروری است.
- شتاب در راستای عمودی یا همان $$y$$ برابر با صفر است.
- مجهولات مسئله نیروی عکس العملِ $$R$$ و شتاب $$a$$ هستند.
در اولین گام مولفه عمودی نیروی وزن که از جانب جرم به سطح وارد می‌شود، برابر است با:
$$ R = mg \cos \theta $$
از طرفی مولفه افقی این نیرو نیز به صورت زیر بدست می‌آید.
$$ \large f _ x = - m g \sin \theta $$
توجه داشته باشید که دلیل قرار دادن علامت منفی در جلوی نیروی فوق، خلاف جهت بودن آن نسبت به محور $$x$$ها است. حال قانون دوم نیوتن را در راستای $$y$$ می‌نویسیم.
$$ \large \begin {align*} \sum F _ y = 0 & \ \ \Rightarrow \ \ mg \cos \theta - R = 0 \end {align*} $$
با توجه به معادله فوق نیروی عکس العمل $$R$$ به صورت زیر بدست می‌آید.
$$ \large \begin {align*} \large R= m g \cos \theta \end {align*} $$
حال قانون دوم را در راستای $$x$$ به صورت زیر می‌نویسیم.
$$ \large \begin {align*} \sum F _ x = 0 & \ \ \Rightarrow \ \ mg \sin \theta - F = m a \end {align*} $$
با حل معادله فوق نیز شتاب $$a$$ بدست خواهد آمد.
$$ \large \begin {align*} a = \frac { mg \sin \theta - F } { m } \end {align*} $$
بنابراین در نهایت نیروی عکس العمل و شتاب a بدست آمدند. توجه داشته باشید که تمامی مسائل سطح شیبدار همانند روش بالا حل می‌شوند. همچنین لازم است بدانید که نیروی $$F$$ هر عاملی می‌تواند باشد. این نیرو می‌تواند توسط یک شخص به جرم وارد شده باشد، یا این که نیروی اصطکاک باشد.
نیروی اصطکاک
همان‌گونه که در مطلب اصطکاک نیز عنوان شد، اندازه این نیرو متناسب با نیروی عمودی است که به سطح وارد می‌شود. برای نمونه مسئله بررسی شده در بالا را به صورتی در نظر بگیرید که سطح دارای ضریب اصطکاک $$ \large \mu $$ باشد.
در این صورت نیروی اصطکاکِ $$F$$ برابر خواهد بود با:
$$ \large F = \mu R = \mu m g \cos \theta $$
با جایگذاری $$F$$ در رابطه مربوط به شتاب، $$a$$ برابر با عدد زیر بدست خواهد آمد.
$$ \large \begin {align*} a = \frac { mg \sin \theta - \mu m g \cos \theta } { m } \end {align*} = g \sin \theta - \mu g \cos \theta $$
این رابطه نشان می‌دهد در هریک از شرایط زیر جسم روی سطح ساکن خواهد ماند.
$$ \large \begin{align} F & \leq \mu R \\ mg \ \sin \theta & \leq \mu mg \ \cos \theta \\ \frac{ \sin \theta } { \cos \theta } & \leq \mu \\ \tan \theta & \leq \mu \end{align} $$
مثال ۱
جسمی به جرم ۴ کیلوگرم را در نظر بگیرید که روی سطحی شیبدار با $$ \large \tan \theta = \frac { 3 } { 4 } $$ قرار گرفته است. با فرض این‌که ضریب اصطکاک برابر با $$ \large \mu = 0.3 $$ باشد، شتاب جرم را بیابید.
با توجه به اطلاعات بیان شده در صورت سوال می‌توان دید که $$ \large \tan \alpha \geq \mu $$ است، بنابراین جسم به حرکت در خواهد آمد. در ابتدا با نوشتن قانون دوم نیوتن در راستای y مقدار نیروی عکس العمل R به صورت زیر بدست می‌آید.
$$ \large \begin {align} F & = m a , \\ R - mg \ \cos \theta &= m \times 0 , \\ R & = mg \ \cos \theta, \\ & = 4 \times 9.8 \times 0.8, \\ & = 31.36 \mathrm { N } \end {align} $$
با توجه به معلوم بودن تانژانت و همچنین روابط مثلثاتی داریم:
$$ \large \cos \theta = \frac{4}{5} = 0.8 \ , \ \sin \theta = \frac { 3 } { 5 } = 0.6 $$
در آخر با نوشتن قانون دوم به صورت زیر، شتاب بدست می‌آید.
$$ \large \begin {align} F & = ma \\ mg \ \sin \theta - \mu R & = ma \\ \left(4 \times 9.8 \times 0.6 \right) - \left ( 0.3 \times 31.36 \right) & = 4 a \\ \frac { 23.52 - 9.408 } { 4 } & = a \\ a & = 3.528 \mathrm { m s ^ { -2 } } \end{align} $$
در ادامه مثالی بررسی شده که در آن نیرویی خارجی نیز به سیستم وارد می‌شود.
مثال ۲
مطابق با شکل زیر جسمی به جرم ۳ کیلوگرم را در نظر بگیرید که توسط نیروی $$ \large 30N $$ و با زاویه $$ \large 25 $$ درجه روی سطح به سمت بالا کشیده می‌شود. با فرض این‌که ضریب اصطکاک سطح برابر با $$ \large \mu = 0.15 $$ باشد، اندازه شتاب را بدست آورید.
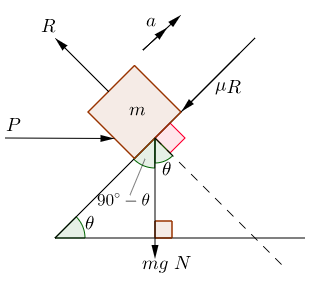
مطابق با شکل فوق در ابتدا جهت حرکت را به سمت بالا فرض کنید. با این فرض در ابتدا قانون دوم نیوتن را در راستای عمود به حرکت $$ (y) $$ می‌نویسیم. با نوشتن این معادله اندازه نیروی عکس العمل سطح $$ (R) $$ بدست خواهد آمد.
$$ \large \begin{align} F & = ma, \\ R - mg \ \cos \theta - 30 \ \cos (90^ {\circ} - \theta) &= m \times 0, \\ R & = mg \ \cos (25^{\circ}) + 30 \ \cos (90 ^ {\circ} - 25), \\ & = (3 \times 9.8 \times 0.906) + (30 \times 0.423), \\ & = 39.324 \mathrm{N} \end{align} $$
با بدست آمدن نیروی عکس العمل، می‌توان قانون دوم نیوتن را در راستای x نوشته و اندازه شتاب را به صورت زیر بدست آورد.
$$ \large \begin{align} F & = ma, \\ 30 \ \cos ( 25 ^ {\circ}) - 3 g \ \cos ( 6 5 ^ {\circ}) - \mu R & = 3a, \\ 27.189 - 12.425 - (0.15 \times 39.324) & = 3 a, \\ a & = 2.955 \mathrm { m s ^ { - 2 } } \end{align} $$
جاده شیبدار
احتمالا شما نیز متوجه شده‌اید که مسیر جاده در هنگام مواجه با پیچ‌ها به صورت شیبدار ساخته می‌شوند. در این قسمت می‌خواهیم دلیل این امر را توضیح دهیم.
در ابتدا فرض کنید ماشینی با سرعت v روی جاده‌ای با زاویه $$ \large \theta $$ در حال حرکت است. در این صورت نیروهای وارد به ماشین به صورت زیر خواهند بود.
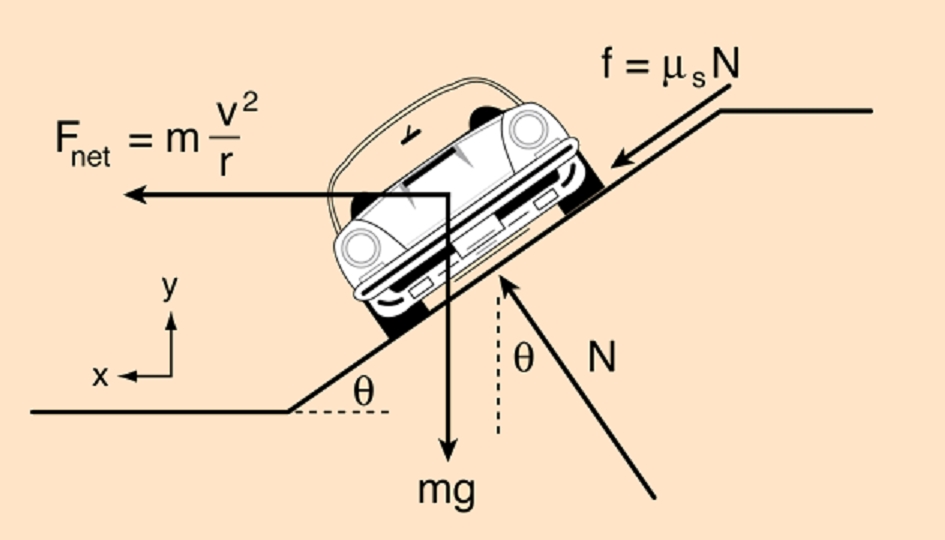
توجه داشته باشید که نیروی عمود به سطح با $$ F _ N $$ نشان داده شده است. فرض کنید شعاع جاده در پیچ برابر با $$r$$ باشد. همان‌طور که در مطلب حرکت دایره‌ای نیز عنوان شد شتاب مرکز‌گرا برای جسمی که روی مسیری با سرعت $$V$$ و به شعاع $$r$$ در حال حرکت است، برابر با $$ \large a = \frac { v ^ 2 } { r } $$ در نظر گرفته می‌شود.
حال این سوال مطرح می‌شود که بیشترین سرعت ممکن برای ماشین که از مسیرش خارج نشود، چقدر است؟
ماشین در بیشترین سرعتش تمایل دارد به سمت بالا حرکت کند. بنابراین جهت نیروی اصطکاک به سمت پایین خواهد بود. در ابتدا با نوشتن قانون دوم در راستای $$x$$ داریم:
$$\large \sum F _ x = m \frac { v ^ 2 } { r } = N \sin \theta + \mu _ s N \cos \theta $$
از طرفی جسم شتابی در راستای عمود ندارد؛ بنابراین قانون دوم نیوتن در راستای $$y$$ نیز برابر است با:
$$\large \sum F _ y = 0 = N \cos \theta - \mu _ s N \sin \theta - m g $$
با حل دو معادله فوق، بیشترین سرعت ممکن برابر با عبارت زیر بدست می‌آید.
$$\large v_ { m a x } = \sqrt { \frac { r g ( \sin \theta + \mu _ s \cos \theta ) } { \cos \theta - \mu _ s \sin \theta } } $$
رابطه فوق نشان می‌دهد که با کاهش زاویه مسیر، بیشترین سرعت ممکن کاهش می‌یابد. در حالتی حدی اگر پیچ جاده زاویه‌ای نداشته باشد، اندازه ماکزیمم سرعت برابر است با:
$$ \large v_{max} = \sqrt { r g \mu _ s } $$
همچنین اگر جاده دارای اصطکاک نباشد، مقدار بیشترین سرعت برابر خواهد بود با:
$$ \large v_{max} = \sqrt { r g \tan \theta } $$
در صورت علاقه‌مندی به مباحث مرتبط در زمینه فیزیک، آموزش‌های زیر نیز به شما پیشنهاد می‌شوند:
ممنون از شما، اگر دو جسم با جرم متفاوت از روی سطح شیب دار رها شوند و با فرض داشتن اصطکاک کدام جسم زودتر به پایین سطح خواهد رسید
سلام و وقت به‌خیر؛
چنانچه تمام شرایط دیگر برای هر دو جسم یکسان در نظر گرفته شود و سطح دارای اصطکاک باشد، جسمی که سبک‌تر است زودتر به پایین سطح خواهد رسید.
سپاس از توجه و همراهی شما با مجله فرادرس.
این کجاش ساده بود