روش غربال اعداد اول — به زبان ساده + مثال و تمرین

در آموزش‌های پیشین مجله فرادرس، با اعداد اول و ویژگی آن‌ها آشنا شدیم. روش‌های متنوعی برای تعیین اعداد اول از میان سایر اعداد وجود دارد. در این آموزش، با روش غربال اعداد اول آشنا می‌شویم و مثال‌های آن را نیز ارائه خواهیم کرد.

آشنایی با اعداد اول

اعداد اول اعدادی هستند که فقط دو عامل دارند و آن دو عامل 1 و خود عدد هستند. به عبارت بهتر، عدد اول تنها بر ۱ و خودش بخش‌پذیر است. برای مثال، عدد 5 که فقط دو عامل 1 و 5 را دارد، یک عدد اول است. اما عدد ۶ را در نظر بگیرید. این عدد بیش از دو عامل دارد، یعنی 1، 2، 3 و 6. این یعنی 6 عدد اول نیست. حال عدد 1 را در نظر بگیرید. می دانیم که این عدد فقط یک عامل دارد. بنابراین، نمی‌تواند یک عدد اول باشد، زیرا همان‌طور که گفتیم یک عدد اول باید دقیقاً دو عامل داشته باشد. این به این معنی است که 1 نه عدد اول است و نه مرکب، بلکه یک عدد منحصر به فرد است.

به عبارت دیگر، اگر عددی را نتوان به گروه‌های مساوی تقسیم کرد، عدد اول است. فقط در صورتی می‌توانیم عددی را به گروه‌هایی با تعداد اجزای مساوی تقسیم کنیم که بتوانیم آن را به‌عنوان حاصل‌ضرب دو عامل بنویسیم. به عنوان مثال، 7 را نمی‌توان به گروه‌هایی با اعداد مساوی تقسیم کرد. این به این دلیل است که 7 را فقط می‌توان به‌صورت زیر نوشت:‌

۷ = ۷ × ۱

۷ = ۱ × ۷

این بدان معناست که ۱ و ۷ تنها عامل‌های 7 هستند. بنابراین، 7 یک عدد اول است، زیرا نمی‌توان آن را به گروه‌های اعداد مساوی تقسیم کرد.

تعریف رسمی عدد اول این‌گونه است: «هر عدد صحیح بزرگ‌تر از 1 که فقط بر 1 و خودش بخش‌پذیر باشد، یک عدد اول است».

فیلم آموزش ریاضی – پایه هشتم در فرادرس

کلیک کنید

ویژگی‌های اعداد اول

برخی از ویژگی‌های مهم اعداد اول در زیر آورده شده است:

• عدد اول یک عدد حسابی بزرگ‌تر از 1 است.
• دقیقاً دو عامل دارد، یعنی 1 و خود عدد.
• فقط یک عدد اول زوج وجود دارد، یعنی 2.
• هر دو عدد اول همیشه نسبت به هم اول هستند.
• هر عدد را می‌توان به‌صورت حاصل‌ضرب اعداد اول بیان کرد.

اعداد اول در مقابل اعداد مرکب

عدد اول عددی بزرگ‌تر از 1 است که دقیقاً دو عامل دارد، در حالی که عدد مرکب بیش از دو عامل دارد. به عنوان مثال، 5 را می‌توان تنها به یک روش فاکتور گرفت، یعنی 1 × 5 (یا) 5 × 1. فقط دو عامل دارد که عبارت‌اند از 1 و 5. بنابراین، 5 یک عدد اول است.

عدد مرکب عددی بزرگ‌تر از 1 است که بیش از دو عامل داشته باشد. به عنوان مثال، 4 را می‌توان به روش‌های مختلف فاکتور گرفت. در واقع، عامل‌های 4 عبارت‌اند از 1، 2، و 4. می‌بینیم که این عدد بیش از دو عامل دارد. بنابراین، 4 یک عدد مرکب است.

برای آشنایی با مباحث ریاضیات دبیرستان، پیشنهاد می‌کنیم به مجموعه فیلم‌های آموزش‌های دروس دبیرستان و پیش دانشگاهی فرادرس مراجعه کنید که لینک آن در ادامه آورده شده است.

• برای مشاهده مجموعه فیلم‌های آموزش‌های دروس دبیرستان و پیش دانشگاهی + اینجا کلیک کنید.

اعداد اول و اعداد هم‌اول

بین مفهوم اعداد اول و اعداد هم‌اول (متباین) تفاوت وجود دارد. اعداد هم‌اول همیشه به‌صورت جفت در نظر گرفته می‌شوند، در حالی که یک عدد را می‌توان به‌عنوان یک عدد اول تفسیر کرد. اگر یک جفت اعداد به غیر از 1 هیچ عامل مشترکی نداشته باشند، آن اعداد را اعداد ‌هم‌اول یا متباین یا اول نسبت به هم می‌نامند. اعداد هم‌اول می‌توانند اول یا مرکب باشند، تنها معیاری که باید رعایت شود این است که این دو عدد مقسوم‌علیه مشترکی نداشته باشند.

نمونه هایی از اعداد هم‌اول در ادامه آورده شده‌اند:

• 5 و 9 هم‌اول هستند.
• 6 و 11 هم‌اول هستند.
• 18 و 35 هم‌اول هستند.

دقت کنید که اعداد هم‌اول لزوماً اعداد اول نیستند.

فیلم آموزش ریاضی پایه هفتم در فرادرس

کلیک کنید

قبل از آشنایی با روش غربال، بهتر است روش شناسایی مضارب اعداد مهم را بررسی کنیم.

مضارب اعداد ۲ و ۳ و ۵

در ادامه، با روش یافتن مضارب اعداد ۲ و ۳ و ۵ آشنا می‌شویم.

مضارب ۲ چه اعدادی هستند؟

مضارب اعداد ۲، اعدادی هستند که رقم سمت راست آن‌ها یکی از رقم‌های ۰، ۲، ۴، ۶ یا ۸ باشد. برای مثال، ۱۲۰، ۲۳۶ و ۴۴۴ مضارب ۲ هستند.

مضارب ۳ چه اعدادی هستند؟

مضارب عدد ۳، اعدادی هستند که مجموع ارقام آن‌ها مضربی از ۳ باشد. برای مثال، عدد ۱۱۴ را در نظر بگیرید. مجموع ارقام این عدد برابر با ۶ = ۴ + ۱ + ۱ است. چون ۶ خود بر ۳ بخش‌پذیر است، پس ۱۱۴ مضربی از ۳ خواهد بود.

مضارب ۵ چه اعدادی هستند؟

اعدادی که رقم سمت راست آن‌ها ۰ یا ۵ باشد، مضربی از ۵ خواهند بود. مثلاً ۱۲۰ و ۱۲۵ مضرب ۵ هستند.

روش غربال اعداد اول

اعداد اول از زمان های قدیم مورد کنجکاوی انسان بوده‌اند. حتی امروزه، ریاضیدانان در تلاش برای یافتن اعداد اول با ویژگی‌های رازآلود هستند. اقلیدس قضیه اعداد اول را مطرح کرد و گفت که تعداد اعداد اول بی‌نهایت است.

اما آیا همه اعداد اول از 1 تا 100 را می‌شناسیم؟ چگونه می‌توانیم این اعداد را مشخص کنیم؟‌ آیا بررسی کرده‌اید که آیا هر عدد بر اعداد کوچک‌تر از خود بخش‌پذیر است؟ این کار قطعاً زمان و تلاش زیادی را می‌طلبد. «اِراتوستِن» یا «اراتوستنِس» (Eratosthenes)، ریاضی‌دان یونانی، یکی از بزرگترین دانشمندانی بود که چند دهه پس از اقلیدس زندگی کرد و روشی هوشمندانه برای تعیین تمام اعداد اول تا یک عدد معین طراحی کرد. این روش «غربال اراتوستن» نامیده می‌شود که به «روش غربال» معروف است. فرض کنید باید اعداد اول تا عدد دلخواه n را پیدا کنیم. بدین منظور، فهرستی از تمام اعداد از ۲ تا n را می‌نویسیم. با شروع از کوچک‌ترین عدد اول، یعنی ۲، شروع می‌کنیم و همه مضرب‌های آن را، جز خود 2، از فهرست حذف می‌کنیم. به‌طور مشابه، همین کار را برا اعداد اول بعد از ۲، یعنی ۳ و ۵ و... انجام می‌دهیم. در ادامه، این روش را با جزئیات و به‌صورت گام به گام شرح خواهیم داد.

نمودار اعداد اول نموداری است که فهرست اعداد اول را به‌ترتیب و نظام‌مند نشان می‌دهد. در زیر نمودار اعداد اول از اعداد 1 تا 100 ارائه شده است که فهرستی از اعداد اول را نشان می‌دهد و با رنگ زرد مشخص شده‌اند. این نمودار با استفاده از روش غربال اعداد اول رسم شده است. در ادامه، این روش را به‌صورت گام به گام معرفی می‌کنیم.

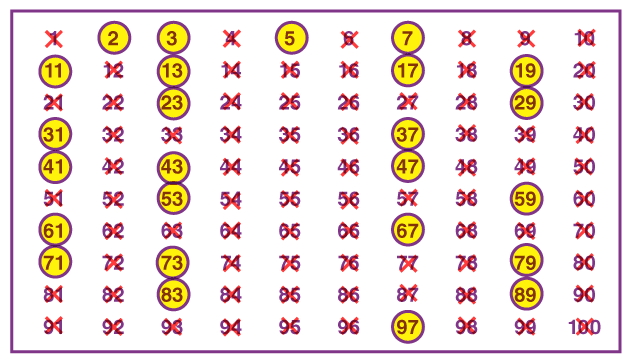
اکنون می‌خواهیم اعداد اول از 1 تا 100 را با استفاده از روش غربال اراتوستن مشخص کنیم. در این روش غربال، اعداد غیر از اعداد اول را حذ می‌کنیم و آنچه باقی می‌ماند، اعداد اول هستند. مراحل جداسازی یا همان غربال اعداد اول از 1 تا 100 به‌شرح زیر است:

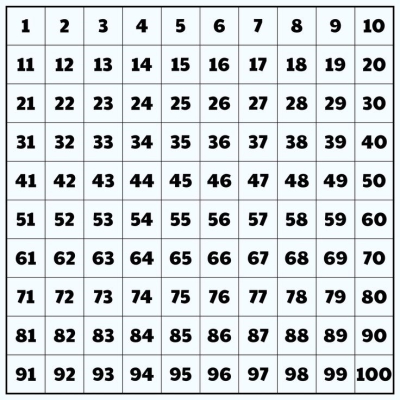
گام 1: ابتدا تمام اعداد از 1 تا 100 را به‌صورت ردیف و ستون مانند شکل زیر بنویسید.

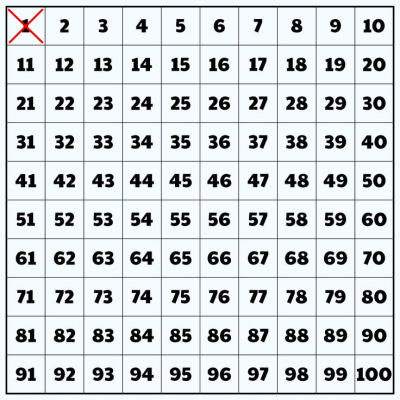
گام 2: یک ضربدر روی 1 بکشید، زیرا نه عدد اول است و نه مرکب.

گام 3: تمام مضرب‌های 2، مانند ۴ و ۶ و ۸ و... را خط بزنید، زیرا همه مضرب‌های 2 اعدادی مرکب هستند.

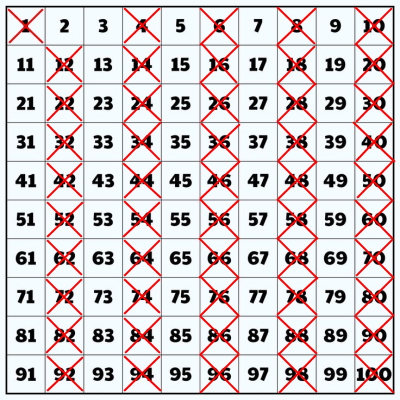
گام 4: تمام مضرب‌های ۳، مانند ۶ و ۹ و ۱۲ و... را خط بزنید، زیرا همه مضرب‌های ۳ اعدادی مرکب هستند. دقت کنید که بعضی از مضرب‌های ۳ مضرب ۲ نیز هستند و در مرحله قبل آن‌ها را خط زده‌ایم.

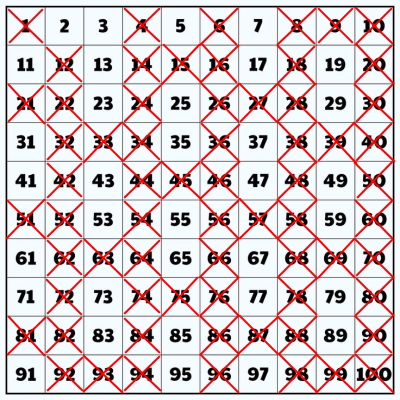
گام 5: مشابه گام‌های قبل، مضاربی از ۵ را که باقی مانده‌اند، حذف می‌کنیم.

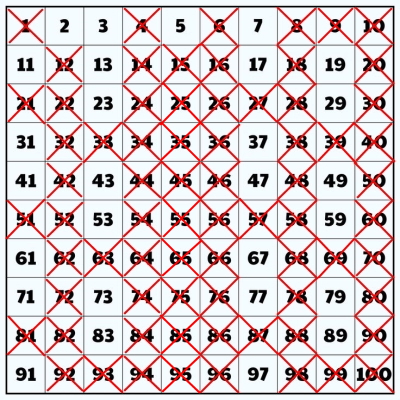
گام 6: اکنون نوبت به حذف کردن مضارب ۷ می‌رسد.

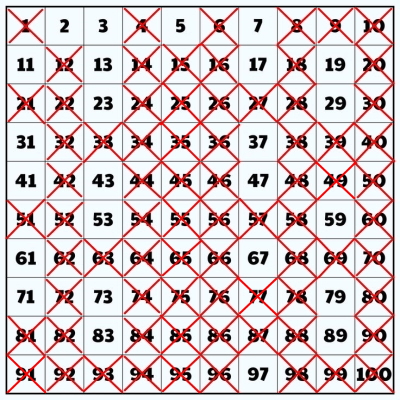
گام 7: در این مرحله، تمام مضرب‌های 11 را خط می‌زنیم. البته می‌بینیم که همه آن‌ها را از قبل خط زده‌ایم.

گام 8: روند را برای سایر اعداد اول، یعنی ۱۳، ۱۷، ۱۹ و... ادامه می‌دهیم و مضاربشان را حذف می‌کنیم. می‌بینیم که مضارب این اعداد را از قبل خط زده‌ایم و آنچه باقی مانده است، اعداد اول هستند. دور آن‌ها یک حلقه می‌کشیم.

روش‌های دیگر برای یافتن اعداد اول

روش های مختلفی برای یافتن اعداد اول وجود دارد. در ادامه، دو مورد از این روش‌ها را مرور کنیم.

روش 1: این روش استفاده از یک فرمول برای اعداد اول بزرگ‌تر از ۴۰ است. در این روش، کافی است از فرمول زیر استفاده کنیم:

$$n^2+n+41$$

و به‌جای $$n$$ اعداد صحیح را قرار می‌دهیم. این فرمول همه اعداد اول بزرگ‌تر از 40 را به ما می‌دهد. چند عدد صحیح را جایگذاری کرده و بررسی کنیم:

• عدد ۰ را قرار می‌دهیم: $$0^2+0+41=0+41=41$$
• عدد ۱ را در فرمول جایگذاری می‌کنیم: $$1^2+1+41=2+41=43$$
• عدد ۲ را در فرمول قرار می‌دهیم:‌ $$2^2+2+41=6+41=47$$

به همین ترتیب، می‌توانیم تمام اعداد اول بزرگ‌تر از 40 را محاسبه کنیم.

روش 2: هر عدد اول به‌غیر از 2 و 3 را می‌توان با فرمول‌های $$6n+1$$ و $$6n-1$$ نوشت. برای مثال، چند عدد اول را با این فرمول‌های می‌نویسیم:

• با در نظر گرفتن $$n=1$$ و فرمول $$6n-1$$ به عدد اول $$6(1)-1=5$$ می‌رسیم.
• با در نظر گرفتن $$n=1$$ و فرمول $$6n+1$$ به عدد اول $$6(1)+1=7$$ می‌رسیم.
• با در نظر گرفتن $$n=2$$ و فرمول $$6n-1$$ به عدد اول $$6(2)-1=11$$ می‌رسیم.
• با در نظر گرفتن $$n=2$$ و فرمول $$6n+1$$ به عدد اول $$6(2)+1=13$$ می‌رسیم.

فیلم آموزش علوم تجربی – پایه هشتم – بخش شیمی در فرادرس

کلیک کنید

مثال روش غربال

در این بخش، مثال‌هایی را از روش غربال بررسی می‌کنیم.

مثال اول روش غربال

اعداد اول بین ۱ و ۲۰ را مشخص کنید.

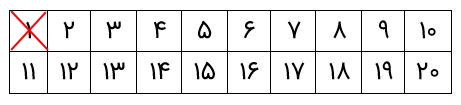
جواب: ابتدا اعداد را در دو ردیف ده‌تایی می‌نویسیم.

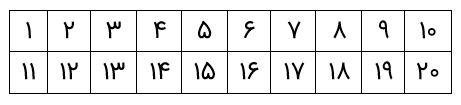
ابتدا عدد ۱ را خط می‌زنیم، چون یک عدد اول نیست.

سپس، دور عدد ۲ خط می‌کشیم، چون یک عدد اول است.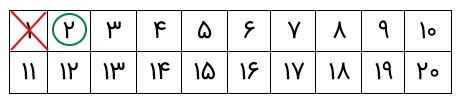

سپس، اعداد مضرب این عدد اول را حذف می‌کنیم.

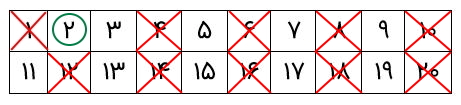
پس از آن، نوبت به عدد اول ۳ می‌رسد. دور آن یک خط می‌کشیم، زیرا فقط بر خودش و ۱ بخش‌پذیر است.

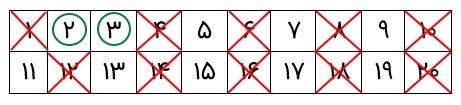
اکنون، مضارب ۳ را حذف می‌کنیم. دقت کنید برخی از آن‌ها را به‌دلیل اینکه مضرب ۲ بوده‌اند، از قبل حذف شده‌اند.

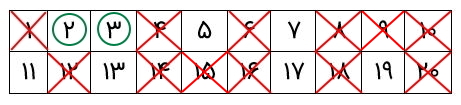
اکنون به عدد ۷ می‌رسیم. می‌بینیم که همه مضاربش را حذف کرده‌ایم. همان‌طور اعداد ۱۱ و ۱۳ و ۱۷ را. بنابراین، دور آن‌ها یک دایره می‌کشیم.

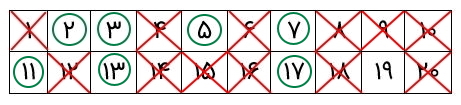
مثال دوم روش غربال

اعداد اول بین ۱۰۱ تا ۱۳۰ را با استفاده از روش غربال تعیین کنید.

جواب: ابتدا اعداد ۱۰۱ تا ۱۳۰ را در یک جدول می‌نویسیم.

ابتدا مضارب ۲ را خط می‌زنیم.

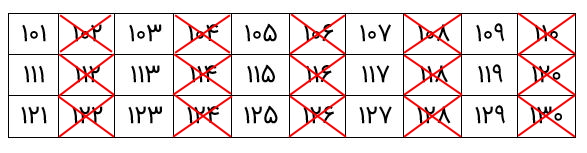
اکنون مضارب عدد اول ۳ را خط می‌زنیم.

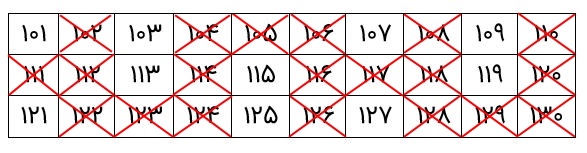
اکنون نوبت به مضارب عدد ۵ می‌رسد که آن‌ها را خط بزنیم.

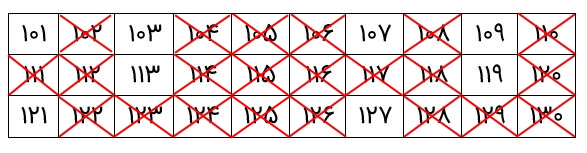
اکنون باید مضارب عدد ۷ را خط بزنیم که عدد ۱۱۹ است.

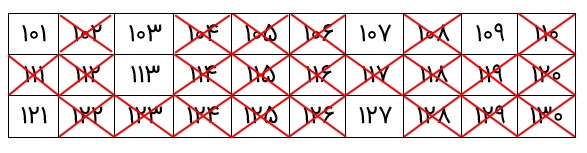
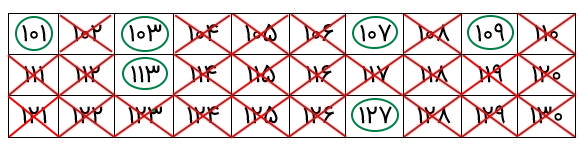
در این مرحله، مضارب عدد ۱۱ را حذف می‌کنیم که عدد ۱۲۱ است.

می‌بینیم که سایر اعدادی که باقی مانده‌اند فقط بر خودشان و ۱ بخش‌پذیر هستند. بنابراین، این اعداد، اعداد اول هستند.