ساخت ربات معامله گر رمزارز با میانگین متحرک ساده در پایتون — بخش اول

انجام معامله، یک فرایند پیچیده است که نیاز به توانایی و آموزش بالایی دارد. همچنین طراحی یک سیستم معاملاتی درست، پایبندی به آن و دخالت ندادن احساسات در معاملات نیز از اهمیت بسیار بالایی برخودار هستند. بخش زیادی از مشکل معاملهگران نتیجه ضعف در رعایت این موارد است. رباتهای معاملهگر (Autotrader Bot) میتوانند با یادگیری رفتار بازار، تحلیل داده، با سرعت و دقت بسیار بالاتری عمل کنند. به همین دلیل، استفاده از علم داده (Data Science)، هوش مصنوعی (Artificial Intelligence) و علم تحلیل تکنیکال (Technical Analysis) در کنار هم، میتواند باعث انجام معاملات بهینه و سودده شود. در این مطلب، با ساخت ربات معامله گر رمزارز آشنا میشویم.
به دلیل استفاده از رباتها از قوانین، روابط و روش کارهای کاملاً مشخص و روشن، به معاملات انجام شده توسط آنها، معاملات الگوریتمی (Algorithmic Trading) گفته میشود. در این مطلب قصد داریم با استفاده از اندیکاتور میانگین متحرک ساده (Simple Moving Average | SMA)، یک سیگنال ایجاد کرده و براساس آن معامله انجام دهیم و سود حاصل را بیشینه کنیم. برای آشنایی با میانگین متحرک ساده میتوانید به مطلب «میانگین متحرک چیست؟ + پیاده سازی Moving Average در پایتون» مراجعه کنید.
ساخت ربات معامله گر رمزارز در پایتون
برای شروع کدنویسی، ابتدا وارد محیط برنامهنویسی شده و کتابخانههای مورد نیاز را فراخوانی میکنیم:
1import numpy as np
2import pyswarm as ps
3import pandas_datareader as pdt
4import matplotlib.pyplot as pltاین کتابخانهها به ترتیب برای موارد زیر استفاده خواهند شد:
- کار با آرایهها و محاسبات برداری
- بیشینهسازی سود ربات با استفاده از الگوریتم بهینهسازی ازدحام ذرات (Particle Swarm Optimization | PSO)
- دریافت داده مربوط به قیمت نمادها
- رسم نمودار
حال تنظیمات زیر را در ابتدای برنامه اعمال میکنیم:
1np.random.seed(0)
2plt.style.use('ggplot')برای پیادهسازی ربات مورد نظر، از کلاس (Class) استفاده میکنیم. با توجه به اینکه قصد داریم از یک مدل خطی برای گرفتن سیگنال از میانگین متحرک ساده استفاده کنیم، به شکل زیر کلاس مورد نظر را تعریف میکنیم:
1class smaLR:حال یک متد (Method) سازنده ایجاد میکنیم:
1 def __init__(self):داخل این متد، یک لیست ایجاد میکنیم. در ادامه برنامه، با هر بار انجام شبیهسازی معامله، سود حاصل به این لیست اضافه خواهد شد تا بعداً بتوانیم روند آموزش ربات را مشاهده کنیم:
1 def __init__(self):
2 self.TrainLog = []به این ترتیب، این متد کامل میشود. متد دیگری نیز ایجاد میکنیم تا مجموعه داده مربوط به قیمت نماد مورد نظر را در بازه زمانی مشخصشده دریافت کند. این متد در ورودی، اسم نماد، تاریخ شروع مجموعه داده و تاریخ پایان مجموعه داده را دریافت میکند:
1 def GetData(self, Ticker:str, Start:str, End:str):حال ورودیهای گرفته شده را داخل شیء (self) ذخیره میکنیم تا در صورت نیاز استفاده کنیم.
1 def GetData(self, Ticker:str, Start:str, End:str):
2 self.Ticker = Ticker
3 self.Start = Start
4 self.End = Endحال میتوانیم مجموعه داده را در قالب یک دیتافریم (Data Frame) دریافت کرده و داخل شیء ذخیره کنیم:
1 def GetData(self, Ticker:str, Start:str, End:str):
2 self.Ticker = Ticker
3 self.Start = Start
4 self.End = End
5 self.DF = pdt.DataReader(Ticker,
6 data_source='yahoo',
7 start=Start,
8 end=End)مجموعه داده حاصل، شامل ستونهای زیر است:
- تاریخ
- بیشترین قیمت معاملهشده در روز (High)
- کمترین قیمت معاملهشده در روز (Low)
- قیمت آغازین (Open)
- قیمت پایانی (Close)
- حجم معاملات (Volume)
- قیمت پایانی تعدیلشده (Adj Close)
با توجه به اینکه تنها ستون مربوط به تاریخ، قیمت آغازین و قیمت پایانی مورد نیاز است، چهار ستون دیگر را به شکل زیر حذف میکنیم:
1 def GetData(self, Ticker:str, Start:str, End:str):
2 self.Ticker = Ticker
3 self.Start = Start
4 self.End = End
5 self.DF = pdt.DataReader(Ticker,
6 data_source='yahoo',
7 start=Start,
8 end=End)
9 self.DF.drop(labels=['High', 'Low', 'Volume', 'Adj Close'],
10 axis=1,
11 inplace=True)به این ترتیب، مجموعه داده دریافت شده و ستونهای اضافی حذف میشود.
حال نیاز داریم متد دیگری تعریف کنیم تا پردازشهای مورد نیاز را بر روی داده انجام دهد. این تابع در ورودی تنها طول میانگین متحرک ساده را دریافت خواهد کرد:
1 def ProcessData(self, L:int):حال مانند آنچه قبلاً انجام شد، طول میانگین متحرک ساده را در شیء ذخیره میکنیم:
1 def ProcessData(self, L:int):
2 self.L = Lحال با استفاده از متدهای rolling و mean موجود در کتابخانه pandas ستون مربوطه به میانگین متحرک ساده با طول L را ایجاد میکنیم:
1 def ProcessData(self, L:int):
2 self.L = L
3 self.DF[f'SMA({L})'] = self.DF['Close'].rolling(L).mean()به این ترتیب، اندیکاتور مورد نظر محاسبه میشود. حال نیاز داریم تا نسبت قیمت در هر روز به مقدار میانگین متحرک ساده را محاسبه کرده و سپس از آن لگاریتم بگیریم:
1 def ProcessData(self, L:int):
2 self.L = L
3 self.DF[f'SMA({L})'] = self.DF['Close'].rolling(L).mean()
4 self.DF[f'Log-Ratio({L})'] = np.log(self.DF['Close'] / self.DF[f'SMA({L})'])توجه داشته باشید که امکان استفاده از خود میانگین متحرک ساده وجود ندارد، زیر علاوه بر اینکه یک اندیکاتور تعقیب روند است، کاربرد آن نیز نسبت به نمودار قیمت است و نه خود مقدار آن.
نسبت قیمت به میانگین متحرک ساده میتواند معیار بهتری باشد، زیرا یک «اسیلاتور» (Oscillator) است، اما حول مقدار ۱ نوسان خواهد کرد. برای رفع این مشکل میتوانیم مقادیر خروجی را منهای ۱ کنیم. از طرفی این معیار قرینه نیست. برای مثال، دو حالت را در نظر بگیرید که در یکی قیمت ۲ برابر میانگین متحرک ساده و در دیگری میانگین متحرک ۲ برابر قیمت است. در این دو حالت مقدار نسبت خواهد بود:
$$ \begin{aligned}
R_{1} &=\frac{ { Close }}{S M A}-1=\frac{2 \times S M A}{S M A}-1=1 \\
R_{2} &=\frac{C l o s e}{S M A}-1=\frac{C l o s e}{2 \times C {lose}}-1=-0.5
\end{aligned} $$
به این ترتیب، مشاهده میکنیم که اعداد حاصل قرینه یکدیگر نیستند. حال اگر از لگاریتم نسبت استفاده کنیم، خواهیم داشت:
$$ \begin{aligned}
L R_{1} &=\log \left(\frac{C {lose}}{S M A}\right)=\log \left(\frac{2 \times S M A}{S M A}\right)=\log 2=0.301 \\
L R_{2} &=\log \left(\frac{C l o s e}{S M A}\right)=\log \left(\frac{Close}{2 \times C {lose}}\right)=\log 0.5=-0.301
\end{aligned} $$
به این ترتیب، میتوان به خوبی مشاهده کرد که لگاریتم نسب قیمت به میانگین متحرک ساده، معیار بهتری است و ویژگی قابل استفاده برای محاسبه سیگنال ایجاد شد.
نیاز است ستون دیگری نیز در مجموعه داده ایجاد شود که قیمت اولین فرصت معامله ممکن را نشان دهد. برای مثال اگر در انتهای روز معاملاتی $$n$$ سیگنال خرید دریافت کردیم، در ابتدای روز $$n+1$$ میتوانیم خرید کنیم، پس قیمت Open روز بعد، به عنوان اولین فرصت معامله امروز تعیین میشود که خواهیم داشت:
1 def ProcessData(self, L:int):
2 self.L = L
3 self.DF[f'SMA({L})'] = self.DF['Close'].rolling(L).mean()
4 self.DF[f'Log-Ratio({L})'] = np.log(self.DF['Close'] / self.DF[f'SMA({L})'])
5 self.DF['FP'] = self.DF['Open'].shift(-1)به این ترتیب تمامی ستونهای مورد نیاز محاسبه و اضافه شدند. با توجه به اینکه برای برخی روزها مقدار میانگین متحرک و برای روز آخر مقدار قیمت آغازین فردا را نداریم، برای این ستونها مقدار NaN یا Not a Number قرار داده میشود که مناسب نیست، به همین دلیل سطرهای شامل NaN را حذف (Drop) میکنیم:
1 def ProcessData(self, L:int):
2 self.L = L
3 self.DF[f'SMA({L})'] = self.DF['Close'].rolling(L).mean()
4 self.DF[f'Log-Ratio({L})'] = np.log(self.DF['Close'] / self.DF[f'SMA({L})'])
5 self.DF['FP'] = self.DF['Open'].shift(-1)
6 self.DF.dropna(inplace=True)تا به اینجا مجموعه داده آماده است. اقدام دیگری که باید انجام شود، محاسبه اندازه مجموعه داده و ذخیره آن است:
1 def ProcessData(self, L:int):
2 self.L = L
3 self.DF[f'SMA({L})'] = self.DF['Close'].rolling(L).mean()
4 self.DF[f'Log-Ratio({L})'] = np.log(self.DF['Close'] / self.DF[f'SMA({L})'])
5 self.DF['FP'] = self.DF['Open'].shift(-1)
6 self.DF.dropna(inplace=True)
7 self.nD = len(self.DF)به این ترتیب، این متد کامل میشود. حال باید روش انجام معامله توسط ربات را تعیین کنیم. برای این کار متد جدید تعریف میکنیم که در ورودی پارامترهای مدل خطی (Linear Model) را دریافت میکند. مدل خطی، با گرفتن مقدار لگاریتم نسبت قیمت به میانگین متحرک ساده، عددی را به عنوان سیگنال برمیگرداند که ربات با توجه به آن تصمیم میگیرد. این مدل را به شکل زیر توصیف میکنیم:
$$\operatorname{Signal} l_{t}=p_{0}+p_{1} \times L R_{t}=p_{0}+p_{1} \times \log \left(\frac{C {los} e_{t}}{S M A_{t}}\right) $$
به این ترتیب، تنها دو پارامتر وجود خواهد داشت. برای متد خواهیم داشت:
1 def Trade(self, Parameters:np.ndarray):با توجه به اینکه این متد در طول بازه زمانی مجموعه داده کار میکند، بهتر است یک تاریخچه از عملکرد آن نیز داشته باشیم. تعداد ۴ آرایه خالی به طول مجموعه داده ایجاد میکنیم:
1 def Trade(self, Parameters:np.ndarray):
2 Moneys = np.zeros(self.nD)
3 Shares = np.zeros(self.nD)
4 Values = np.zeros(self.nD)
5 Signals = np.zeros(self.nD)این ۴ آرایه به ترتیب موارد زیر را در خود ذخیره میکنند:
- پول آزاد موجود در هر لحظه از زمان
- سهام موجود در هر لحظه از زمان
- ارزش پرتفوی (Portfolio Value) ایجاد شده در هر لحظه از زمان
- سیگنال ایجادشده در هر لحظه از زمان
دو «دیکشنری» (Dictionary) دیگر نیز برای ذخیره روزهایی که خرید یا فروش انجامشده ایجاد میکنیم:
1 def Trade(self, Parameters:np.ndarray):
2 Moneys = np.zeros(self.nD)
3 Shares = np.zeros(self.nD)
4 Values = np.zeros(self.nD)
5 Signals = np.zeros(self.nD)
6 Buys = {'Time':[], 'Price':[]}
7 Sells = {'Time':[], 'Price':[]}حال یک «سرمایه اولیه» (Budget) و تعداد سهام اولیه را تعیین میکنیم:
1 def Trade(self, Parameters:np.ndarray):
2 Moneys = np.zeros(self.nD)
3 Shares = np.zeros(self.nD)
4 Values = np.zeros(self.nD)
5 Signals = np.zeros(self.nD)
6 Buys = {'Time':[], 'Price':[]}
7 Sells = {'Time':[], 'Price':[]}
8 money = 1
9 share = 0حال باید به ازای هر روز داده معاملات انجام شود:
1 def Trade(self, Parameters:np.ndarray):
2 Moneys = np.zeros(self.nD)
3 Shares = np.zeros(self.nD)
4 Values = np.zeros(self.nD)
5 Signals = np.zeros(self.nD)
6 Buys = {'Time':[], 'Price':[]}
7 Sells = {'Time':[], 'Price':[]}
8 money = 1
9 share = 0
10 for i in range(self.nD):ابتدا قیمت اولین فرصت معامله، لگاریتم نسبت قیمت به میانگین متحرک ساده و سیگنال را محاسبه میکنیم:
1 def Trade(self, Parameters:np.ndarray):
2 Moneys = np.zeros(self.nD)
3 Shares = np.zeros(self.nD)
4 Values = np.zeros(self.nD)
5 Signals = np.zeros(self.nD)
6 Buys = {'Time':[], 'Price':[]}
7 Sells = {'Time':[], 'Price':[]}
8 money = 1
9 share = 0
10 for i in range(self.nD):
11 fp = self.DF['FP'][i]
12 lr = self.DF[f'Log-Ratio({self.L})'][i]
13 signal = Parameters[0] + Parameters[1] * lrحال در این مرحله، ربات سیگنال مربوط به روز مربوط را دارد. برای انجام معامله، تنها دو حالت خواهیم داشت:
- اگر سیگنال مثبت بود و تعداد سهام صفر بود، به اندازه کل پول موجود خرید انجام میدهیم.
- اگر سیگنال منفی بود و تعداد سهام بیشتر از صفر بود، کل سهام را میفروشیم.
توجه داشته باشید که این شیوه از معامله، به هیچ وجه توصیه نمیشود و صرفاً برای سادگی الگوریتم به این شکل در نظر گرفته شده است.
حال شرط اول را پیادهسازی میکنیم:
1 def Trade(self, Parameters:np.ndarray):
2 Moneys = np.zeros(self.nD)
3 Shares = np.zeros(self.nD)
4 Values = np.zeros(self.nD)
5 Signals = np.zeros(self.nD)
6 Buys = {'Time':[], 'Price':[]}
7 Sells = {'Time':[], 'Price':[]}
8 money = 1
9 share = 0
10 for i in range(self.nD):
11 fp = self.DF['FP'][i]
12 lr = self.DF[f'Log-Ratio({self.L})'][i]
13 signal = Parameters[0] + Parameters[1] * lr
14 if signal > 0 and share == 0:
15 share = money / fp
16 money = 0به این شکل، معامله خرید در شرایط گفتهشده انجام میشود. برای ذخیره این معامله نیز، به شکل زیر عمل میکنیم:
1 def Trade(self, Parameters:np.ndarray):
2 Moneys = np.zeros(self.nD)
3 Shares = np.zeros(self.nD)
4 Values = np.zeros(self.nD)
5 Signals = np.zeros(self.nD)
6 Buys = {'Time':[], 'Price':[]}
7 Sells = {'Time':[], 'Price':[]}
8 money = 1
9 share = 0
10 for i in range(self.nD):
11 fp = self.DF['FP'][i]
12 lr = self.DF[f'Log-Ratio({self.L})'][i]
13 signal = Parameters[0] + Parameters[1] * lr
14 if signal > 0 and share == 0:
15 share = money / fp
16 money = 0
17 Buys['Time'].append(i)
18 Buys['Price'].append(fp)حال فرایند مشابه را برای معامله فروش نیز مینویسیم:
1 def Trade(self, Parameters:np.ndarray):
2 Moneys = np.zeros(self.nD)
3 Shares = np.zeros(self.nD)
4 Values = np.zeros(self.nD)
5 Signals = np.zeros(self.nD)
6 Buys = {'Time':[], 'Price':[]}
7 Sells = {'Time':[], 'Price':[]}
8 money = 1
9 share = 0
10 for i in range(self.nD):
11 fp = self.DF['FP'][i]
12 lr = self.DF[f'Log-Ratio({self.L})'][i]
13 signal = Parameters[0] + Parameters[1] * lr
14 if signal > 0 and share == 0:
15 share = money / fp
16 money = 0
17 Buys['Time'].append(i)
18 Buys['Price'].append(fp)
19 elif signal < 0 and share > 0:
20 money = share * fp
21 share = 0
22 Sells['Time'].append(i)
23 Sells['Price'].append(fp)
به این ترتیب، همه معاملهها انجام خواهند شد. برا ذخیره عملکرد و تاریخچه ربات، در انتهای هر روز معاملات، پول، سهام، ارزش پرتفوی و سیگنال را در آرایههای ایجاد شده ذخیره میکنیم:
1 def Trade(self, Parameters:np.ndarray):
2 Moneys = np.zeros(self.nD)
3 Shares = np.zeros(self.nD)
4 Values = np.zeros(self.nD)
5 Signals = np.zeros(self.nD)
6 Buys = {'Time':[], 'Price':[]}
7 Sells = {'Time':[], 'Price':[]}
8 money = 1
9 share = 0
10 for i in range(self.nD):
11 fp = self.DF['FP'][i]
12 lr = self.DF[f'Log-Ratio({self.L})'][i]
13 signal = Parameters[0] + Parameters[1] * lr
14 if signal > 0 and share == 0:
15 share = money / fp
16 money = 0
17 Buys['Time'].append(i)
18 Buys['Price'].append(fp)
19 elif signal < 0 and share > 0:
20 money = share * fp
21 share = 0
22 Sells['Time'].append(i)
23 Sells['Price'].append(fp)
24 Moneys[i] = money
25 Shares[i] = share
26 Values[i] = money + share * fp
27 Signals[i] = signalبه این ترتیب، به ازای هر روز، شروط بررسی میشود، در صورت نیاز معامله میشود و در نهایت اطلاعت تاریخچه ذخیره میشود. معیار مهمی که در انتهای این تابع محاسبه شود، میانگین سود روزانه است. فرض کنید که در ابتدای معاملات ارزش پرتفوی ربات $$v_1$$ اشت و پس از $$n$$ روز، ارزش آن به $$v_2$$ رسیده است. در این شرایط، میانگین درصد سود هر روز به شکل زیر خواهد بود:
$$ v_{2}=v_{1} \times\left(1+\frac{r}{100}\right)^{n-1} $$
با توجه به اینکه در $$n$$ روز معاملاتی، تنها $$n-1$$ بار امکان دریافت سود دارد، باید توان عبارت ضریب $$n-1$$ باشد.
با حل رابطه فوق، مقدار $$r$$ خواهد بود:
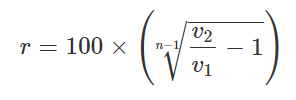
حال این رابطه را در برنامه پیاده میکنیم و در نهایت موارد محاسبهشده را برمیگردانیم:
1 def Trade(self, Parameters:np.ndarray):
2 Moneys = np.zeros(self.nD)
3 Shares = np.zeros(self.nD)
4 Values = np.zeros(self.nD)
5 Signals = np.zeros(self.nD)
6 Buys = {'Time':[], 'Price':[]}
7 Sells = {'Time':[], 'Price':[]}
8 money = 1
9 share = 0
10 for i in range(self.nD):
11 fp = self.DF['FP'][i]
12 lr = self.DF[f'Log-Ratio({self.L})'][i]
13 signal = Parameters[0] + Parameters[1] * lr
14 if signal > 0 and share == 0:
15 share = money / fp
16 money = 0
17 Buys['Time'].append(i)
18 Buys['Price'].append(fp)
19 elif signal < 0 and share > 0:
20 money = share * fp
21 share = 0
22 Sells['Time'].append(i)
23 Sells['Price'].append(fp)
24 Moneys[i] = money
25 Shares[i] = share
26 Values[i] = money + share * fp
27 Signals[i] = signal
28 Return = 100 * ((Values[-1] / Values[0])**(1 / (self.nD - 1)) - 1)
29 return Moneys, Shares, Values, Signals, Buys, Sells, Returnبه این ترتیب متد Trade کامل میشود. حال، نیاز به متد دیگری داریم تا بتواند مقدار تابع هزینه (Loss Function) را برگرداند. توجه داشته باشید که تابع هزینه باید کمینهسازی (Minimization) شود، در حالی که خروجی متد Trade مقدار سود است که باید بیشینهسازی (Maximization) شود. برای رفع این مشکل، تعریف میکنیم:
$$\operatorname{Loss}(P)=-\operatorname{Return}(P) $$
به این ترتیب، با کمینهسازی تابع هزینه، درصد میانگین سود روزانه بیشینه میشود. حال متد مورد نظر را تعریف میکنیم که پارامترها را دریافت کرده و قرینه درصد میانگین سود روزانه را برگرداند:
1 def Loss(self, P:np.ndarray):
2 Return = self.Trade(P)[-1]
3 return -Returnبرای اینکه بعداً بتوانیم مقدار سود در طول آموزش و بهبود آن را ببینیم، مقدار سود را در فهرست تعبیه شده ذخیره میکنیم:
1 def Loss(self, P:np.ndarray):
2 Return = self.Trade(P)[-1]
3 self.TrainLog.append(Return)
4 return -Returnحال این متد نیز کامل است.
تنها متد باقیمانده که باید پیادهسازی شود، مربوط به آموزش دادن مدل است. این متد تعداد مراحل کار الگوریتم PSO و تعداد ذرات را در ورودی میگیرد:
1 def Train(self, MaxIteration:int, SwarmSize:int):حال حد بالا و پایین پارامترها را تعیین میکنیم که اعداد $$+1$$ و $$-1$$ هستند:
1 def Train(self, MaxIteration:int, SwarmSize:int):
2 lb = -1 * np.ones(2)
3 ub = +1 * np.ones(2)حال الگوریتم PSO را روی تابع هزینه اجرا و خروجیها را تعریف میکنیم:
1 def Train(self, MaxIteration:int, SwarmSize:int):
2 lb = -1 * np.ones(2)
3 ub = +1 * np.ones(2)
4 self.P, BestLoss = ps.pso(self.Loss,
5 lb,
6 ub,
7 swarmsize=SwarmSize,
8 maxiter=MaxIteration)حال نتایج بهینهسازی را نمایش میدهیم:
1 def Train(self, MaxIteration:int, SwarmSize:int):
2 lb = -1 * np.ones(2)
3 ub = +1 * np.ones(2)
4 self.P, BestLoss = ps.pso(self.Loss,
5 lb,
6 ub,
7 swarmsize=SwarmSize,
8 maxiter=MaxIteration)
9 BestReturn = -BestLoss
10 print('_'*50)
11 print('Optimization Result:')
12 print(f'\tBest Parameters: {self.P}')
13 print(f'\tBest Return: {BestReturn} %')
14 print('_'*50)به این ترتیب، این تابع نیز کامل میشود. توجه داشته باشید که هدف این تابع محاسبه بهترین پارامترها بود که با اسم P داخل شی ذخیره میشود.
ایجاد شیء و فراخوانی متدها
حال میتوانیم یک شیء از کلاس ایجاد کنیم و به ترتیب متدهای مورد نیاز را فراخوانی کنیم:
1Trader = smaLR()
2
3Trader.GetData('BTC-USD', '2019-01-01', '2022-01-01')
4
5Trader.ProcessData(60)
6
7Trader.Train(50, 60)به این ترتیب:
- ابتدا ربات ایجاد میشود.
- دادههای 3 سال بین $$2019-01-01$$ و $$2022-01-01$$ برای رمزارز بیتکوین (Bitcoin) دریافت میشود.
- یک میانگین متحرک ساده ۶۰ روزه بر روی داده محاسبه و سپس لگاریتم نسبت قیمت به میانگین متحرک ساده محاسبه میشود.
- در نهایت نیز ۶۰ ذره ایجاد و به تعداد ۵۰ مرحله بر روی مجموعه داده آموزش داده میشود.
پس از اجرای کد تا این مرحله، نتایج زیر حاصل میشود:
1__________________________________________________
2
3Optimization Result:
4 Best Parameters: [-0.00912918 0.18591647]
5 Best Return: 0.29836380166610166 %
6__________________________________________________به این ترتیب، مشاهده میکنیم که ربات به میانگین سود روزانه 0.2983 درصد رسیده است. برای محاسبه میانگین درصد سود ماهیانه به شکل زیر عمل میکنیم:
$$r_{30}=100 \times\left(\left(1+\frac{r_{1}}{100}\right)^{30}-1\right) \%=9.347 \% $$
به این ترتیب، انتظار ماهیانه ما از ربات، ۹ درصد سود به صورت ماهیانه است. توجه داشته باشید که این محاسبات به صورت ساده و با پیشفرضهایی انجام شده است که در دنیای واقعی ممکن است برآورده نشود.
این نتیجه با پارامترهای زیر حاصل شده است:
$$\begin{aligned}
&p_{0}=-0.0091 \\
&p_{1}=+0.1859
\end{aligned}$$
حال اگر این اعداد را در رابطه قرار دهیم، تابع سیگنال حاصل میشود:
$$\operatorname{Signal}_{t}=p_{0}+p_{1} \times L R_{t}=-0.0091+0.1859 \times \log \left(\frac{\operatorname{Close} _{t}}{S M A_{t}}\right) $$
با قرار دادن قیمت و مقدار میانگین متحرک، میتوان به صورت دستی سیگنال را محاسبه و معامله کرد. توجه داشته باشید که این پارامترها برای میانگین متحرک ساده با پنجره زمانی ۶۰ روزه و برای داده ۳ سال مشخص شده از نماد بیتکوین بهینهسازی شده است. با تغییر هر کدام از این شرایط، باید بهینهسازی در شرایط جدید تکرار شود. پس از اجرا، میتوانیم نمودار سود در طول آموزش را رسم کنیم:
1plt.plot(Trader.TrainLog, ls='-', lw=0.8, c='crimson')
2plt.title('Model Return Over Function Evaluations')
3plt.xlabel('Function Evaluation')
4plt.ylabel('Average Daily Return (%)')
5plt.show()که شکل زیر را خواهیم داشت.

به این ترتیب، مشاهده میکنیم که ربات از سودهای بسیار پایین و حتی منفی، به مقدار تقریباً ۰٫۲۹۸۳ نزدیک میشود، هرچند که برخی ذرات نتوانستهاند به این نقطه همگرا (Converge) شوند. توجه داشته باشید که تابع Trade به تعداد ۳۰۰۰ بار اجرا شده است، به عبارت دیگر، ربات ۳۰۰۰ ترکیب مختلف از پارامترها را تا انتهای این دوره امتحان کرده است و دارای تجربه معامله به اندازه ۹۰۰۰ سال است!
حال میتوانیم برای نمایش نتایج، یک بار دیگر متد Trade را با پارامترهای بهینه اجرا کنیم:
1_, _, Values, Signals, Buys, Sells, Return = Trader.Trade(Trader.P)به این ترتیب، تاریخچه مربوط به بهترین عملکرد حاصل میشود.
ابتدا میتوانیم نمودار «نیمه-لگاریتمی» (Semi-Logarithm) مربوط به قیمت، میانگین متحرک ساده در یک نمودار و ارزش پرتفوی را به همراه روند رشد سرمایه را در نمودار دیگر در مقابل هم رسم کنیم:
1plt.subplot(1, 2, 1)
2plt.semilogy(Trader.DF['Close'].to_numpy(), ls='-', lw=0.8, c='k', label='Close')
3plt.semilogy(Trader.DF['SMA(60)'].to_numpy(), ls='-', lw=1, c='b', label='SMA(60)')
4plt.title('Price Over Time')
5plt.xlabel('Time (Day)')
6plt.ylabel('Price ($)')
7plt.legend()
8
9plt.subplot(1, 2, 2)
10MeanValue = (1 + Return / 100)**np.arange(start=0, stop=Values.size, step=1)
11plt.semilogy(Values, ls='-', lw=0.8, c='crimson', label='Real Values')
12plt.semilogy(MeanValue, ls='--', lw=1, c='k', label=f'Mean Values (Return: {round(Return, 4)} %)')
13plt.title('Value Over Time')
14plt.xlabel('Time (Day)')
15plt.ylabel('Value')
16plt.legend()
17
18plt.show()توجه داشته باشید که متغیر MeanValue درواقع نقطه ابتدای نمودار ارزش پرتفوی را به انتهای آن وصل میکند که به کمک میانگین درصد سود روزانه محاسبه میشود و نمایی است. پس از اجرا کد فوق، نمودار زیر حاصل میشود.
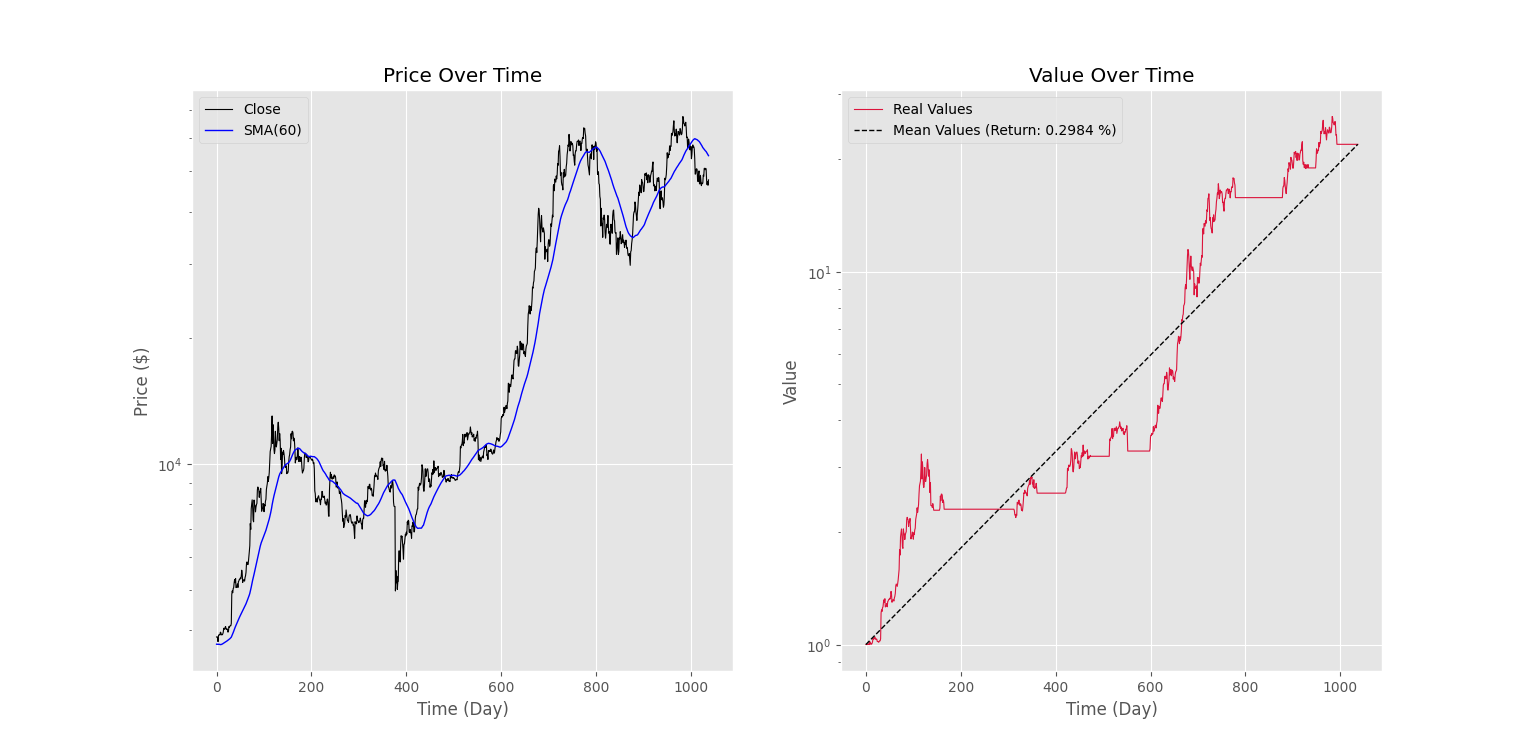
مشاهده میکنیم که نمودار ارزش پرتفوی در برخی بازهها مسطح شده است که به معنی خروجی از سهم است. با تطبیق دو نمودار با یکدیگر، متوجه میشویم که تقریباً در بازههایی که قیمت زیر میانگین متحرک ساده بوده، ربات از سهم خارج شده است. به نوعی، ربات به صورت خودآموز یاد گرفته است که حرکت قیمت به زیر میانگین متحرک نمایی، سیگنالی برای فروش و برعکس است. نکته دیگری که وجود دارد، این است که ربات با گرفتن ۱ واحد سرمایه در ابتدا، آن را در طول ۱۰۳۸ روز به ۲۱٫۹۶ واحد تبدیل کرده است. نماد بیتکوین در این مدت، از قیمت ۳۸۵۹ دلار به ۴۷۶۸۶ دلار رشد کرده است. میتوان نشان داده که عملکرد ربات ۱٫۸۴ برابر بهتر بوده است:
$$\frac{\frac{21.96-1}{1}}{\frac{47686-3859}{3859}}=1.84$$
به این ترتیب، مشهود است که انجام معاملات در این بازه توسط ربات، به اندازه ٪۸۴ سود سرمایهگذاری را افزایش داده است. حال میتوانیم در نمودار دیگری، نمودار قیمت، میانگین متحرک نمایی و در زیر آن نمودار سیگنال را رسم کنیم:
1plt.subplot(3, 1, (1, 2))
2plt.semilogy(Trader.DF['Close'].to_numpy(), ls='-', lw=0.8, c='k', label='Close')
3plt.semilogy(Trader.DF['SMA(60)'].to_numpy(), ls='-', lw=1, c='b', label='SMA(60)')
4plt.title('Price Over Time')
5plt.ylabel('Price ($)')
6plt.legend()
7
8plt.subplot(3, 1, 3)
9Z=np.zeros_like(Signals)
10plt.plot(Signals, ls='-', lw=0.7, c='k')
11plt.fill_between(np.arange(Signals.size), Signals, Z, where=(Signals > Z), color='lime', alpha=0.9, label='Buy Signal')
12plt.fill_between(np.arange(Signals.size), Signals, Z, where=(Signals < Z), color='crimson', alpha=0.9, label='Sell Signal')
13plt.axhline(ls='-', lw=1, c='b')
14plt.title('Signal Over Time')
15plt.xlabel('Time (Day)')
16plt.ylabel('Value')
17plt.legend()
18
19plt.show()پس از اجرای این کد نیز شکل زیر را خواهیم داشت.
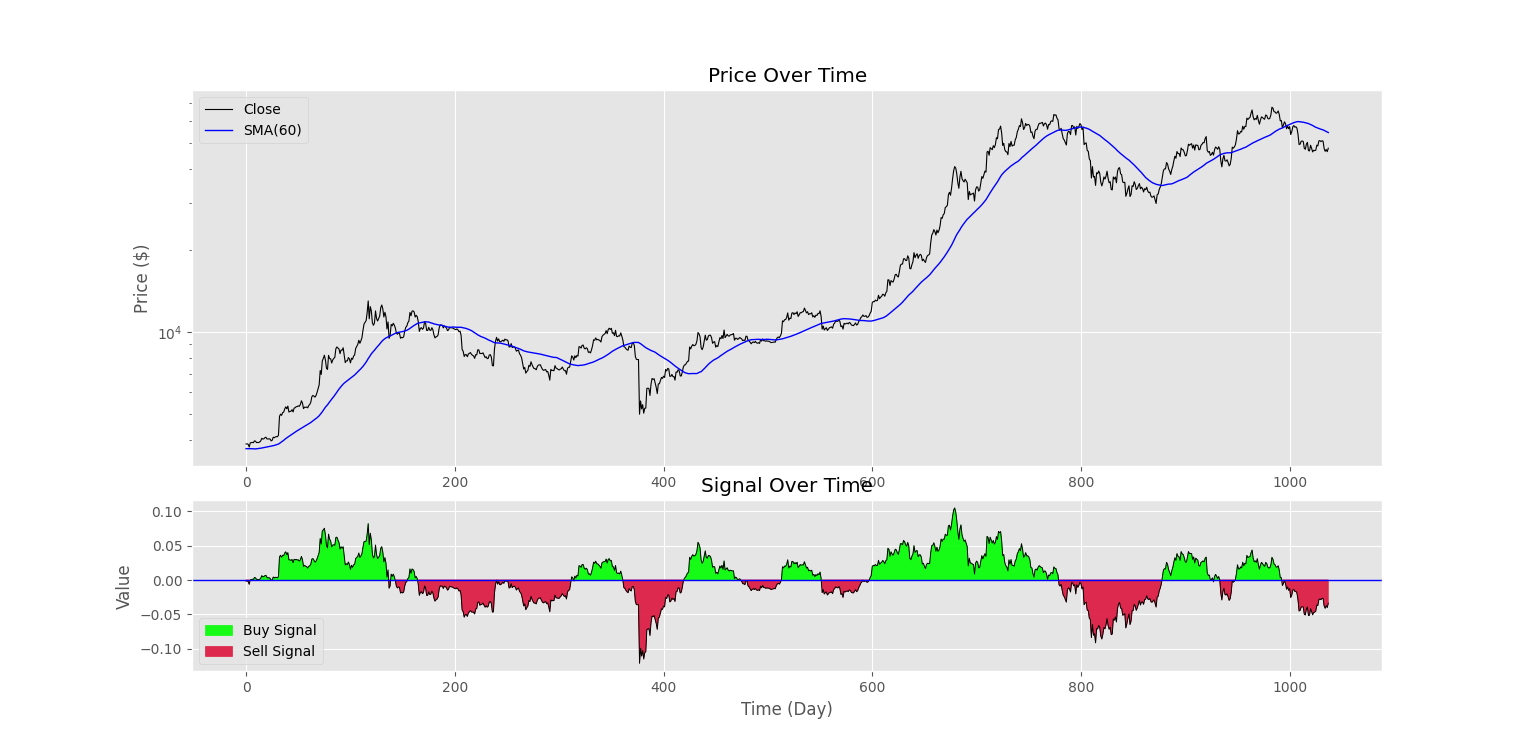
به این ترتیب، تطابق نمودار سیگنال با میانگین متحرک ساده به خوبی مشاهده میشود. برای نمودار آخر، میتوانیم نقاط خرید و فروش ربات را روی نمودار قیمت نشان دهیم.
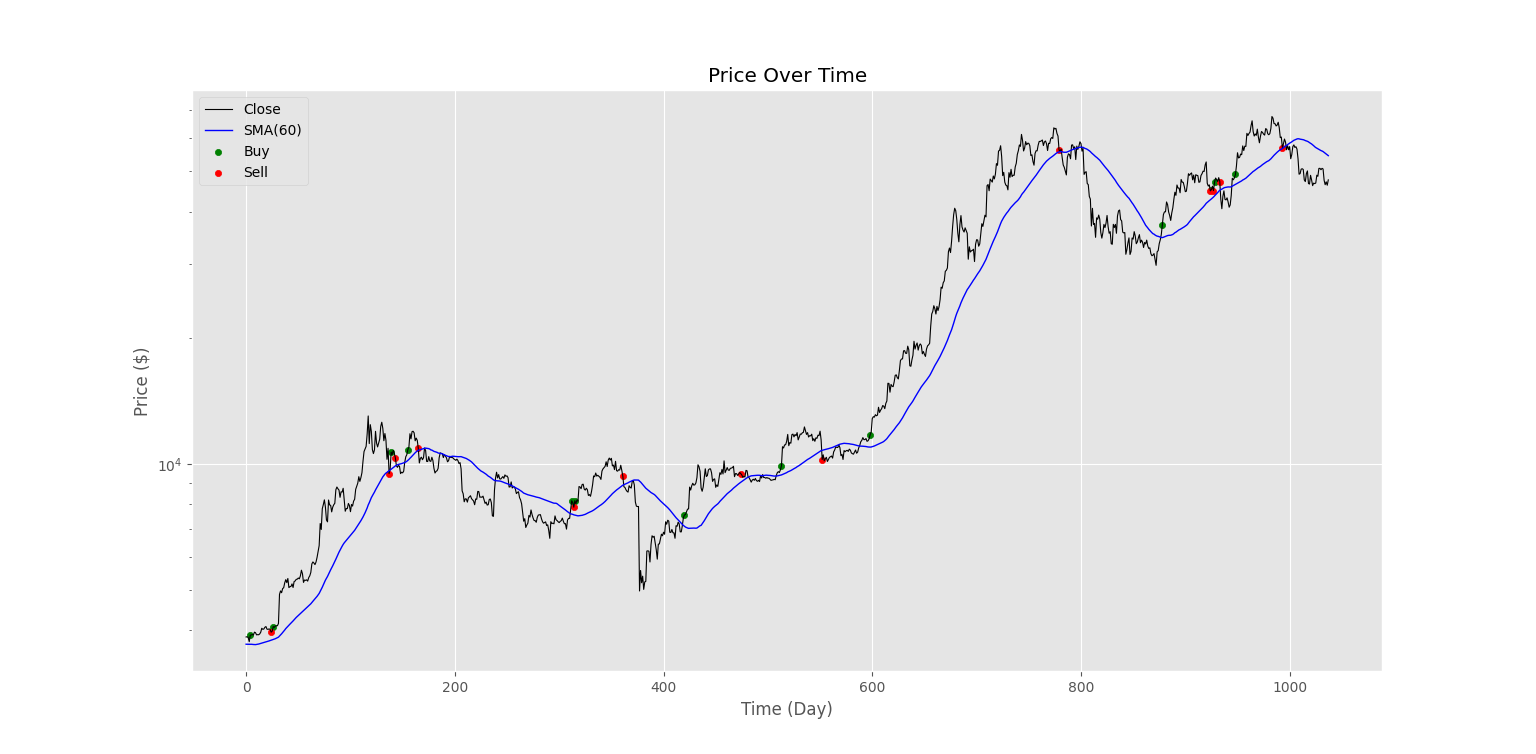
به این ترتیب، مشاهده میکنیم که ربات دقیقاً پس از شکست میانگین متحرک ساده وارد معامله نشده و اندکی اختلاف وجود دارد که با توجه به بهینهسازی انجام شده قابل توجیه است. توجه داشته باشید که برای شرایطی که تنها از یک اندیکاتور استفاده میکنیم، شاید مقدار مناسب پارامترها قبال حدس باشد، اما در شرایطی که از چندین اندیکاتور و به شکل مدلهای پیچیدهتر استفاده میکنیم، اهمیت الگوریتم بهینهسازی مشخص میشود. در نهایت، میتوانیم برای بیشینهسازی سود حاصل، طول بازه میانگین متحرک ساده را بهینهسازی کنیم. برای این کار برنامه را به ازای Lهای مختلف اجرا میکنیم و جدول زیر حاصل میشود.
| Return (%) | L (Day) |
| 0.2478 | 5 |
| 0.2406 | 8 |
| 0.2556 | 13 |
| 0.2661 | 21 |
| 0.3005 | 34 |
| 0.2762 | 40 |
| 0.3003 | 45 |
| 0.2973 | 55 |
| 0.2983 | 60 |
| 0.2905 | 65 |
| 0.2976 | 70 |
| 0.2681 | 89 |
به این ترتیب مشاهده میکنیم که یک میانگین متحرک ساده با طول بازه حدود ۳۴ روز میتوان انتخاب بهتری باشد.
جمعبندی
در این مطلب توانستیم یک ربات طراحی کنیم که میتواند به کمک یک میانگین متحرک ساده، معاملات خودکار انجام دهد و نتایج خوبی ایجاد کند. برای مطالعه بیشتر میتوان موارد زیر را بررسی کرد:
- چگونه میتوان از یک میانگین متحرک نمایی (Exponential Moving Average | EMA) به جای میانگین متحرک ساده استفاده کرد؟ حدس میزنید بازده ربات چه مقدار و در چه جهت تغییر کند؟
- برنامه را روی اندازه نمادها اجرا کنید و بازدهها را با یکدیگر مقایسه کنید. تفاوت از کجا حاصل میشود؟ آیا شباهتی بین پارامترهای نهایی وجود دارد؟
- چگونه میتوانیم معیاری برای نشان دادن مزیت ربات نسبت به Hold کردن طراحی کنیم؟
- برای برخی نمادها امکان انجام معاملات Short وجود دارد. چگونه میتوان این امکان را در برنامه ایجاد کرد؟ با اضافه شدن این امکان، بازده ربات به چه شکل تغییر میکند؟
- اگر بخواهیم بین دو نماد که ربات برای هر دو سیگنال خرید گرفته است، یکی را انتخاب کنیم، کدامیک باید انتخاب شود؟ چرا؟
- یک معاملهگر باید علاوه بر بیشینهسازی سود، ریسک معاملات را نیز تا جای ممکن کاهش دهد. چگونه میتوان ریسک هر نماد را محاسبه کرد؟
- نتایج ربات ایجاد شده، تنها بر روی دادههای آموزش (Train Dataset) محاسبه شد. چگونه میتوان یک مجموعه داده آزمایش (Test Dataset) ایجاد کرد؟ این مجموعه باید از کدام بخش مجموعه داده انتخاب شود؟
- اگر بخواهیم از دو میانگین متحرک ساده با طولهای متفاوت برای محاسبه سیگنال استفاده کنیم، معادله سیگنال به چه صورت خواهد بود؟ حدس میزنید بازده ربات در این شرایط به چه صورت تغییر خواهد کرد؟










سلام این شکلها کدوم برنامه پایتون هست نصب کنم شکل ها که برنامه نویسی کنم بیاد ممنون
سلام، برای رسم نمودارها از کتابخانه Matplotlib پایتون استفاده شده است.
سلام و عرض ادب آقای دکتر از زحمات شما متشکرم.
استاد من میخوام برنامه نویسی یاد بگیرم و هدفم نوشتن اندیکاتور و اکسپرت برای متاتریدر و تریدینگ ویو هست تا نیازهای شخصیم رفع کنم. به نظر شما پایتون میتونه راه ساده تر و جامع باشه یا نیاز به زبان دیگری است؟
منظورم اینه که پایتون هم میتونه کارهای زبان mql را انجام بده و میشه باهاش اندیکاتور اکسپرت شخصی نوشت و در محیط متاتریدر استفاده کرد؟
در زبان برنامهنویسی پایتون، امکانات بیشتری نسبت به زبان برنامهنویسی MQL وجود دارد. در صورتی که نیاز به این امکانات جدید داشته باشید، یادگیری زبان پایتون توصیه میشود، در غیر این صورت، میتوانید با MQL ادامه دهید.
کتابخانههایی در پایتون وجود دارد که برای کار با زبان MQL طراحی شدهاند.
موفق باشید.
منظورم اینه اگر پایتون را هم یاد بگیرم میتونم باهاش اندیکاتور و اکسپرت های شخصی خودم که در متاتریدر برای فارکس نیاز دارم رو هم بنویسم یا پایتون این قدرت رو نداره و نمیتونه کار زبان mql رو انجام بده؟
سلام، در صورتی که قصد دارید اندیکاتور و اکسپرتهای مد نظر خودتان را پیادهسازی کنید، شاید چندان نیازی به پایتون نباشد. پایتون یا زبانهای برنامهنویسی دیگر، برای گسترش روشهای موجود با عنوان اندیکاتور و اکسپرت کاربردی میباشد، در صورتی که قصد فعالیت در این حد را ندارید، استفاده از زبانههای برنامهنویسی مربوط به خود Meta Trader و Trading View میتواند بهتر باشد.
واقعا عالی بود .از اقای دکتر کلامی واقعا کمال تشکر را داریم . مطالب بسیار علمی و مفید هستند. سپاس فراوان
سلام، خیلی ممنون از بازخورد و همراهی شما. موفق باشید.