الگوریتم بهینه سازی ازدحام ذرات – کد الگوریتم PSO | راهنمای جامع
در این مطلب، الگوریتم بهینه سازی ازدحام ذرات (Particle Swarm Optimization | PSO) به طور کامل و همراه با مثال مورد بررسی قرار گرفته و پیادهسازی الگوریتم PSO در پایتون، متلب و جاوا انجام شده است. شایان توجه است که به منظور تشریح محاسبات ریاضی نهفته در پس الگوریتم بهینه سازی ازدحام ذرات یا همان الگوریتم PSO از نسخه کلاسیک این الگوریتم استفاده خواهد شد. در مطلب «الگوریتم بهینه سازی ازدحام ذرات | کد الگوریتم PSO در پایتون ، متلب و جاوا | راهنمای جامع» ابتدا به مفهوم بهینهسازی پرداخته شده و سپس، الگوریتم بهینه سازی ازدحام ذرات به طور جامع و کامل مورد بررسی قرار گرفته است. در ادامه مطلب، انواع الگوریتم بهینه سازی ازدحام ذرات تشریح میشود. همچنین، روشهای ترکیبی موجود با بهرهگیری از الگوریتم بهینه سازی ازدحام ذرات که ترکیبی از روشهای بهینهسازی هیوریستیک و قطعی هستند نیز معرفی میشوند.


علاوه بر پرداختن به مباحث بیان شده، در مطلب «الگوریتم بهینه سازی ازدحام ذرات | کد الگوریتم PSO در پایتون ، متلب و جاوا | راهنمای جامع» چالشهای اساسی که کاربر ضمن استفاده از الگوریتم PSO با آنها مواجه میشود نیز مورد بررسی قرار گرفتهاند. یک بررسی موردی (Case Study) نیز با بهرهگیری از الگوریتم بهینه سازی ازدحام ذرات یا همان الگوریتم PSO انجام شده است که به درک بهتر مبحث کمک میکند. این مثال پیرامون بهینهسازی تابع هزینه برای سیستم تولید مثل با استفاده از الگوریتم PSO در بهینهسازی ترکیبی است. در نهایت، پیادهسازی الگوریتم بهینه سازی ازدحام ذرات در پایتون، متلب و جاوا انجام شده است.
مقدمهای بر بهینهسازی و الگوریتمهای آن
«بیشینه» (Maximizing) کردن «سود» یا «کمینه» (Minimizing) کردن «زیان» (Loss) از جمله مسائل بسیار حائز اهمیت در زمینههای گوناگون از جمله حوزههای فنی و مهندسی است. در یک تعریف ساده و کوتاه میتوان گفت که مسائلی که در آنها هدف بیشینه یا کمینه کردن یک تابع است را «مسئله بهینهسازی» (Optimization Problem) میگویند. برای مطالعه بیشتر پیرامون بهینهسازی، مطالعه مطالب «بهینه سازی (ریاضیاتی) چیست؟ — راهنمای جامع» و «بهینه سازی چند هدفه چیست؟ — راهنمای جامع» پیشنهاد میشود.
با توسعه فناوری، تعداد و پیچیدگی مسائل بهینهسازی نیز در زمینههای علمی گوناگون افزایش پیدا کرده است. از متداولترین مسائل موجود در حوزههای مهندسی که نیاز به استفاده از روشهای بهینهسازی برای حل آنها وجود دارد میتوان به تبدیل و توزیع انرژی، لجستیک (Logistics | آمادگاری) و بارگذاری مجدد رآکتورهای هستهای اشاره کرد. مسائل بهینهسازی در دیگر زمینهها از جمله هندسه و اقتصاد نیز کاربرد دارند. از دیگر زمینههای اصلی کاربرد بهینهسازی میتوان به «هوش مصنوعی» (Artificial Intelligence | AI) و یادگیری ماشین «Machine Learning» اشاره کرد.
برای بیشینه یا کمینه کردن یک تابع به منظور پیدا کردن نقطه یا نقاط بهینه، رویکردهای گوناگونی وجود دارند و قابل استفاده هستند. با وجود طیف گسترده الگوریتمهای بهینهسازی که وجود دارند، یک الگوریتم خاص که برای همه مسائل بهترین گزینه باشد وجود ندارد. در واقع، یک روش بهینهسازی که برای یک مسئله مناسب است، ممکن است برای مسئله دیگری مناسب نباشد. مناسب بودن یک الگوریتم برای یک مسئله، بستگی به ویژگیهای گوناگونی دارد که از جمله آنها میتوان به مشتقپذیر بودن تابع و تقعر آن (محدب یا مقعر بودن) اشاره کرد.
برای آشنایی بیشتر با روشهای انتخاب بهترین الگوریتم برای یک مسئله خاص، مطالعه مطلب «روش انتخاب الگوریتم داده کاوی — راهنمای کاربردی» پیشنهاد میشود. یکی از مهمترین موضوعات در انتخاب روش مناسب برای یک مسئله بهینهسازی، آشنایی کارشناس با انواع الگوریتمها است تا بتواند مناسبترین الگوریتم برای یک مسئله بهینهسازی را انتخاب کند. در این مطلب، یکی از الگوریتمهای محبوب بهینهسازی یعنی الگوریتم بهینه سازی ازدحام ذرات مورد بررسی قرار گرفته و پیادهسازی الگوریتم PSO در متلب ، پایتون و جاوا انجام شده است. برای آشنایی با دیگر الگوریتمهای بهینهسازی، مطالعه مطالب زیر پیشنهاد میشود.
- رویکرد هوش ازدحامی با استفاده از کلونی زنبور عسل مصنوعی برای حل مسائل بهینهسازی
- حل مسائل خوشهبندی با استفاده از الگوریتم کلونی زنبور عسل مصنوعی
- الگوریتم بهینه سازی فاخته – از صفر تا صد
- الگوریتم کرم شب تاب — از صفر تا صد
- الگوریتم ژنتیک – از صفر تا صد
- گرادیان کاهشی (Gradient Descent) و پیاده سازی آن در پایتون — راهنمای کاربردی
- الگوریتم کلونی مورچگان — از صفر تا صد
- الگوریتم بهینه سازی کلونی مورچگان در جاوا — راهنمای کاربردی
- شبیه سازی تبرید (Simulated Annealing) – به زبان ساده
- بهینه سازی نسبت طلایی — از صفر تا صد (+ دانلود فیلم آموزش رایگان)
- مهمترین الگوریتمهای یادگیری ماشین (به همراه کدهای پایتون و R) — بخش یازدهم و پایانی: الگوریتمهای ارتقای گرادیان
الگوریتم بهینه سازی ازدحام ذرات (PSO)
در اوایل سال ۱۹۹۰ میلادی، پژوهشهای گوناگونی پیرامون رفتار اجتماعی گروههای حیوانات انجام شد. این پژوهشها حاکی از آن بودند که برخی از حیوانات که به یک گروه خاص متعلق هستند، مانند پرندگان، ماهیها و دیگر موارد، قادر به آن هستند که اطلاعات را در گروههای (دستههای | گلههای) خودشان به اشتراک بگذارند و چنین قابلیتی به این حیوانات مزایای قابل توجهی برای بقا اعطا میکرد.
با الهام گرفتن از این مطالعات، «کندی» (Kennedy) و «ابِرهارت» (Eberhart) در سال ۱۹۹۵ الگوریتم بهینه سازی ازدحام ذرات (Particle Swarm Optimization | PSO) یا الگوریتم PSO را در یک مقاله معرفی کردند. الگوریتم بهینه سازی ازدحام ذرات یا الگوریتم PSO یک الگوریتم «فراابتکاری» (Metaheuristic) است که برای بهینهسازی توابع پیوسته غیر خطی مناسب محسوب میشود. نویسندگان مقاله مذکور، الگوریتم بهینه سازی ازدحام ذرات یا الگوریتم PSO را از مفهوم هوش ذرات (Swarm Intelligence) که معمولا در گروههای حیوانات مانند گلهها و دستههای حیوانات وجود دارد الهام گرفته و ساختهاند.

برای شفاف شدن هر چه بیشتر ساز و کار کلی الگوریتم بهینه سازی ازدحام ذرات و دیگر الگوریتمهایی که از رفتار گروهی حیوانات الهام گرفته شدهاند، توضیحاتی پیرامون رفتار گروهی (گلهای) حیوانات ارائه میشود. این توضیحات میتواند به درک چگونگی ساخت الگوریتم بهینه سازی ازدحام ذرات (و دیگر الگوریتمهای دارای رویکرد مشابه) برای حل مسائل پیچیده ریاضی کمک کند.
الگوریتم بهینه سازی ازدحام ذرات و رفتار گروهی حیوانات
دسته پرندگانی (گروه پرندگان | ازدحام پرندگان) که بر فراز یک منطقه در حال حرکت هستند، باید یک نقطه را برای فرود پیدا کنند. در این حالت، تعریف اینکه همه پرندگان در کدام نقطه باید فرود بیایند، مسئله پیچیدهای است. زیرا پاسخ این مسئله، وابسته به موضوعات مختلفی یعنی بیشینه کردن منابع غذایی در دسترس و کمینه کردن خطر وجود شکارچیان است در نقطه محل فرود است. در این شرایط، ناظر میتواند حرکت پرندگان را به صورت رقصپردازی ببیند. پرندگان به طور همزمان در یک برهه از زمان حرکت میکنند تا بهترین محل برای فرود آمدن تعیین شود و همه دسته (گروه) به طور همزمان فرود بیایند.
در مثال بیان شده پیرامون حرکت ازدحامی پرندگان و فرود همزمان آنها، اعضای دسته پرندگان (گروه پرندگان) یا همان ازدحام پرندگان، امکان به اشتراکگذاری اطلاعات با یکدیگر را دارند. در صورتی که پرندگان امکان به اشتراکگذاری اطلاعات با یکدیگر را در گروههای خودشان نداشته باشند، هر پرندهای از گروه (دسته) در محل (نقطه) و در زمان متفاوتی فرود میآید.
پژوهشهایی که از سال ۱۹۹۰ پیرامون رفتار پرندگان انجام شد، حاکی از آن است که همه پرندگان یک ازدحام (گروه | دسته) که به دنبال نقطه خوبی برای فرود هستند، قادر به آن هستند که از بهترین نقطه برای فرود در هنگامی که آن نقطه توسط یکی از اعضای ازدحام پیدا شد، آگاه شوند. با استفاده از این آگاهی، هر یک از اعضای این ازدحام، تجربه دانش شخصی و ازدحامی خود را متوازن میکنند که با عنوان «دانش اجتماعی» (Social Knowledge) شناخته شده است.
شایان ذکر است که معیارهایی که برای ارزیابی خوب یا نامناسب بودن یک نقطه برای فرود مورد بررسی قرار میگیرند، شرایط بقایی هستند که در یک نقطه، برای بقا وجود خواهند داشت. از جمله این موارد، بیشینه بودن منابع غذایی و کمینه بودن خطر وجود شکارچیان است که پیشتر نیز به آنها اشاره شد. مسئله پیدا کردن بهترین نقطه برای فرود، یک مسئله بهینهسازی محسوب میشود. گروه، ازدحام یا گله باید بهترین نقطه فرود، برای مثال طول و عرض جغرافیایی را، به منظور بیشینه کردن شرایط بقای اعضای خود تعیین کند.

برای انجام این کار، هر پرندهای ضمن پرواز، به جستجوی نقطه مناسب فرود میپردازد و نقاط مختلف را از جهت معیارهای بقای گوناگون مورد ارزیابی قرار میدهد تا بهترین منطقه برای فرود را پیدا کند و این کار تا زمانی انجام میشود که بهترین منطقه برای فرود، توسط کل ازدحام مشخص شود.
کندی و اِبِرهارت، از رفتار جمعی پرندگان الهام گرفتند؛ رفتاری که مزایای بقای قابل توجهی را برای پرندگان در هنگام جستجو برای یک نقطه امن برای فرود تضمین میکرد. آنها بر همین اساس، الگوریتمی را ارائه کردند که الگوریتم ازدحام ذرات (Particle Swarm Optimization) نامیده میشود. الگوریتم PSO میتواند رفتاری به مثابه آنچه برای دسته پرندگان گفته شد را تقلید کند.
الگوریتم بهینه سازی ازدحام ذرات کلاسیک
نسخه اولیه الگوریتم ازدحام ذرات یا الگوریتم PSO که با عنوان نسخه کلاسیک این الگوریتم نیز شناخته شده است، در سال ۱۹۹۵ ارائه شد. از آن زمان تاکنون، انواع دیگری از این الگوریتم به عنوان نسخههای دیگر الگوریتم کلاسیک ارائه شدهاند که از جمله آنها میتوان به «کاهش خطی وزن اینرسی» (Linear-Decreasing Inertia Weight)، «وزن عامل انقباض» (The Constriction Factor Weight) و «اینرسی پویا» (Dynamic Inertia) در کنار مدلهای ترکیبی یا حتی روشهای بهینهسازی الهام گرفته شده از کوانتوم که روی الگوریتم PSO اعمال شدهاند اشاره کرد.
در مطلب «الگوریتم بهینه سازی ازدحام ذرات | کد الگوریتم PSO در پایتون ، متلب و جاوا | راهنمای جامع»، علاوه بر نسخه کلاسیک، مدل اینرسی PSO نیز به عنوان یک الگوریتم لبه علم مورد بررسی قرار میگیرد. شایان توجه است که فرد برای درک دیگر انواع الگوریتمهای مشتق شده از PSO، ابتدا باید نسخه کلاسیک این الگوریتم را بیاموزد.
هدف از مسائل بهینهسازی، تعیین متغیری است که با بردار X=[x1x2x3…xn] نشان داده میشود و بسته به فرمول بهینهسازی ارائه شده توسط تابع f(X)، بیشینه یا کمینه میشود. بردار متغیر X، به عنوان یک بردار مثبت شناخته شده است. این بردار، یک مدل متغیر و بردار n بُعدی آن را نمایش میدهد که در آن، n نشانگر تعداد متغیرهایی است که ممکن است در مسئله تعیین شوند. n در مسئله پیدا کردن بهترین نقطه برای فرود دسته پرندگان، طول و عرض جغرافیایی است.
از سوی دیگر، تابع f(X) تابع برازش (Fitness Function) یا تابع هدف (Objective Function) نامیده میشود و تابعی است که میزان خوب یا بد بودن یک موقعیت X را ارزیابی میکند. این تابع برای مسئله دسته پرندگان، میزان خوب بودن یک نقطه برای فرود است که پرنده پس از پیدا کردن یک نقطه به آن فکر میکند. چنین ارزیابی برای مسئله فرود گروه پرندگان، براساس معیارهای بقای گوناگون انجام میشود. اکنون، ازدحامی با P ذره در نظر گرفته میشود؛ یک بردار مکان و یک بردار سرعت در هر تکرار برای هر یک از i ذرهای این سرعت را ایجاد میکنند، به صورت زیر وجود دارد:
این بردارها بر اساس بُعد j مطابق با معادلهای که در ادامه آمده است، به روز رسانی میشوند:
و
که در آنها، داریم:
i = 1, 2, …, P و j = 1, 2, …, n.
معادله اول نشانگر آن است که سه عامل مختلف در حرکت ذرات در یک تکرار، نقشآفرین هستند. بنابراین، سه عبارت در این رابطه وجود دارد که بعدا مورد بررسی قرار خواهند گرفت. در عین حال، معادله دوم، موقعیت ذرات را بهروزرسانی میکند. پارامتر w ثابت وزن اینرسی است و برای نسخه کلاسیک PSO، این مقدار یک مقدار مثبت ثابت است. در نسخه کلاسیک PSO، مقدار پارامتر w مثبت است. این پارامتر برای متوازن کردن جستجوی سراسری حائز اهمیت است که به آن اکتشاف (هنگامی که مقادیر بالاتری تنظیم شدهاند) و جستجوی محلی (وقتی مقادیر کمتری تنظیم شدهاند) نیز گفته میشود. یکی از مهمترین تفاوتهای الگوریتم PSO کلاسیک با دیگر نسخههای مشتق شده از این الگوریتم، پارامتر w است.
سرعتی که اولین عبارت در معادله را به روز رسانی میکند، ضرب داخلی پارامتر w و سرعت پیشین ذره است. به همین دلیل است که حرکت پیشین ذره به حرکت کنونی نمایش داده میشود. از همین رو، برای مثال، اگر w = 1 بود، حرکت ذره به طور کامل به وسیله حرکت قبلی خودش تحت تاثیر قرار گرفته است؛ بنابراین، ذره ممکن است به حرکت خود در همان جهت ادامه دهد.
از سوی دیگر، اگر ، این تاثیر کاهش پیدا میکند و این یعنی ذرات به منطقه دیگری در ناحیه جستجو میروند. بنابراین، با توجه به کاهش پارامتر وزن اینرسی، ازدحام (گروه | دسته) ممکن است نواحی بیشتری را در ناحیه جستجو مورد اکتشاف قرار دهد و این یعنی شانس پیدا کردن بهینه سراسری افزایش پیدا میکند. اگرچه، در حالاتی که از مقادیر w کمتر استفاده میشود نیز هزینهای وجود دارد که شبیهسازیها را زمانبرتر خواهد کرد.
عبارت درک فردی که دومین عبارت در معادله یک است، به وسیله تفاضل بین بهترین موقعیت خود ذره، برای مثال و موقعیت کنونی آن محاسبه میشود. شایان توجه است که ایده نهفته در پس این ایده آن است که هر چه فعالیتها فاصله بیشتری از موقعیت بگیرند، تفاضل باید افزایش پیدا کند. بنابراین، این عبارت افزایش پیدا کرده و ذره را به بهترین موقعیت آن جذب میکند. پارامتر که به صورت حاصلضرب در این رابطه وجود دارد، یک ثابت مثبت و یک پارامتر شناخت فردی محسوب میشود و به اهمیت تجربیات پیشین خود ذره وزن میدهد.
دیگر پارامتری که ضرب عبارت دوم را شکل میدهد، عبارت است. یک پارامتر مقدار تصادفی با طیف [0,1] است. این پارامتر تصادفی، نقش مهمی را بازی میکند، زیرا از همگرایی پارامترها ممانعت و بهینه سراسری احتمالی را بیشینه میکند. در نهایت، سومین عبارت مربوط به یادگیری اجتماعی است. به دلیل وجود این پارامتر، همه ذرات در ازدحام قادر به آن هستند که اطلاعات پیرامون بهترین نقطه به دست آمده را صرف نظر از اینکه کدام ذره آن را پیدا کرده است، با یکدیگر به اشتراک بگذارند؛ برای مثال . فرمت این عبارت نیز درست مانند دومین عبارت است که مربوط به یادگیری فردی میشود. بنابراین، تفاضل مانند یک جاذبه برای ذرات برای بهترین نقطه تا هنگام پیدا شدن نقطه در تکرار t عمل میکند. به طور مشابه، پارامتر یادگیری اجتماعی و وزن آن، اهمیت یادگیری سراسری ذرات است. همچنین، نیز نقشی مشابه با دارد.
در ادامه، الگوریتم PSO ارائه شده است و افراد ممکن است متوجه منطق بهینهسازی موجود در جستجوهای آن برای کمینهها شوند و همه بردارهای مکانی که توسط تابع f(X) ارزیابی میشوند. تابع f(X) با عنوان «تابع برازش» (Fitness Function) شناخته شده است. در تصاویر ۲ و ۳ نیز به روز رسانیهایی در سرعت ذرات و موقعیت آن در تکرار t با در نظر داشتن مسئله دوبُعدی با متغیرهای و انجام شده است.
- مقداردهی اولیه
- برای هر i در جمعیت ازدحام با اندازه p:
- را به طور تصادفی مقداردهی اولیه کن.
- $$$$x_{i}$V_{i}f(X_{i})pbestij_{ij}X_{i}X_{i}V_i^tX_i^tf(X_i^t)pbest_{i} \leftarrow X_i^tgbest \leftarrow X_i^tx^{k+1} = x^{k}+a^{k}d^{k}x^{k+1} = x^{k}+a^{k}d^{k}$$
$$d^{k} = -\triangledown(x^{k})+\gamma^{k}d^{k-1}\gamma\gamma^{k}=\frac{\parallel-\triangledown(x^{k})\parallel^{2}}{\parallel-\triangledown(x^{k-1})\parallel^{2}}x^{k+1}=x^{k}+\alpha^{k}d^{k}$$
$$d^{k}=-\mid{H(x)}\mid^{-1}\triangledown{U(x^{k})}x^{k+1} = x^{k} + a^{k} d^{k}$$
$$d^{k} = -H^{k} \triangledown{U} (x^{k})$$
$$H^{k} = H^{k-1} + M^{k-1} + N^{k-1}$$
$$
M^{k-1}=\left[1+\frac{\left(Y^{k-1}\right)^{T} \cdot H^{k-1} \cdot Y^{k-1}}{\left(Y^{k-1}\right)^{T} \cdot d^{k-1}}\right] \frac{d^{k-1} \cdot\left(d^{k-1}\right)^{T}}{\left(d^{k-1}\right)^{T} \cdot Y^{k-1}}
$$$$N^{k-1} = -\frac{d^{k-1} (Y^{k-1})^T H^{k-1} + H^{k-1} Y^{k-1} (d^{k-1})^T)}{(d^{k-1})^T}$$
$$Y^{k-1} = \triangledown{U} (x^{k}) - \triangledown{U} (x^{k-1})Z_{AC} = (\frac{C_{11} \dot{m}_a}{C_{12} - \eta_{AC}})(\frac{P_{2}} {P_{1}}) ln(\frac{P_{2}} {P_{1}})Z_{cc} = (\frac{C_{21}\dot{m}_a} {{C}_{22}-\frac{P_4}{P_3}})Z_{GT} = (\frac{C_{31}\dot{m}_{g}}{C_{32}-\eta_{GT}})ln(\frac{P_4}{P_5} )[1+exp(C_{33}T_{4}-C_{34})]Z_{APH} = C_{41}(\frac{\dot{m}(h_5-h_6)}{(U)(\triangledown{TLM})})^{0.6}Z_{HRSG} = C_{51}((\frac{Q_{PH}}{(\triangledown{TLM})_{PH}})^{0.8}+(\frac{Q_{PH}}{(\triangledown{TLM})_{PH}})^{0.8})+C_{52}\dot{m}_{st}+C_{53}\dot{m}_g^{1.2}$$</p> <p>عبارت کلی برای نرخ هزینه مربوط به سرمایهگذاری (S/$) برای هر مولفه در معادله زیر داده شده است.</p> <p dir=
معادله زیر نشانگر هزینه کلی نرخ عملیات است.
$$" />F = c_{1}\dot{m}_1PCI + \dot{Z}_{AC}+\dot{Z}_{APH}+\dot{Z}_{GT}+\dot{Z}_{HRSG}\frac{P_{2}}{P_{1}}(\eta_{CA})(\eta_{GT})(T_{3})(T_{4})$$
- مکان: برای مثال، هنگامی که متغیر طراحی به دو (صفحه) محدود شده است، یک ذره بر اساس مختصات آن تعریف میشود (x,y).
- سرعت: این مقداری است که برای حرکت دادن محل ذره به سمت بهترین راه حل انجام میشود.
- در PSO محلی، به اشتراک گذاری اطلاعات بین هر ذره و همسایگان مستقیم آن است. در اینجا، حرکت ذرات در هر تکرار، تحت تاثیر بهترین موقعیت محلی شناخته شده آن قرار میگیرد. ذره و همسایههای آن یک توپولوژی ساختار داده حلقهای را تشکیل میدهند.
- PSO سراسری، که در آن به اشتراکگذاری بین هر ذره و بهترین ذرهها از میان همه ذرات که به وسیله بهترین مکان تعیین شدهاند، انجام میشود. این بهترین مکان است که حرکات همه ذرات دیگر را در هر تکرار هدایت میکند. در اینجا، ذرات به صورت توپولوژی ساختار ستارهای سازماندهی شدهاند.
- ذرات به طور تصادفی و با استفاده از «توزیع یکنواخت» (Uniform Distribution) مقداردهی اولیه میشوند.
- به روز رسانیها با استفاده از نسخه اندکی ویرایش شده الگوریتم اصلی (ویرایش توسط نویسندگان مقاله اصلی انجام شده) انجام میشود. در ادامه، کد پایتون برای پیادهسازی الگوریتم PSO ساده ارائه شده است.
- نقطه اولیه اهمیت زیادی در کارایی الگوریتم بهینهسازی دارد. به عنوان یک قاعده سر انگشتی، هرچقدر که نقطه اولیه از بهینه دور باشد، همانقدر طول میکشد تا الگوریتم همگرا شود. (این مورد برای همه الگوریتمهای بهینهسازی صحت دارد.)
- PSO یک الگوریتم تصادفی است و به روز رسانیها با استفاده از یک فرایند تصادفی انجام میشوند. این امر موجب میشود که پیگیری راه حل برای اجرای چند فرایند بهینهسازی دشوار باشد. اگرچه، همیشه میتوان از دانهدهی (Seed) برای اعداد تصادفی استفاده کرد.
- این الگوریتم همیشه راه حل بهینه سراسری را پیدا نمیکند، اما در پیدا کردن بهینهای که بسیار نزدیک به بهینه سراسری است، عملکرد بسیار خوبی دارد. برای تابع sphere بهینه سراسری در (0, 0, 0) است. کد الگوریتم PSO در پایتون که در اینجا ارائه شده است، نقطه دیگری را پیدا میکند که خیلی بد نیست.
- بسته به تعداد ذرات، همگرایی ممکن است زمان بیشتری طول بکشد. به طور کلی، بهتر است که این کار بیش از ۵۰ تکرار طول نکشد.
- برای توابع دشوار، ممکن است نیاز به تکرارهای بیشتری پیش از پیدا کردن بهترین راه حل باشد. برای مثال، میتوان بین ۵۰۰ تا ۱۰۰۰ تکرار داشت.
برای بهینهسازی تابع هدف، سه روال بهینهسازی در ترکیب با PSO با روشهای قطعی متفاوت به صورتی که در جدول زیر نمایش داده شده است، مورد استفاده قرار گرفتهاند.
هیوریستیک قطعی ترکیب ۱ ازدحام ذرات گرادیان هممزدوج ترکیب ۲ ازدحام ذرات شبه نیوتون ترکیب ۳ ازدحام ذرات نیوتون برای حل معادله ترمودینامیکی این مسئله، شبیهسازی تخصصی فرایند IPSEpro® نسخه ۶.۰ مورد استفاده قرار گرفته است. IPSEpro® یک شبیهسازی فرایند است که برای مدلسازی و شبیهسازی سیستمهای حرارتی مختلف از طریق معادلات ترمودینامیکی آنها استفاده میشود. این برنامه به وسیله «سیمتک» (SimTech) توسعه پیدا کرده و دارای یک رابط کاربرپسند و همچنین، طیف وسیعی از مولفهها است که به کاربر امکان مدلسازی و شبیهسازی نیروگاههای متداول، سیستمهای تولید همزمان، چرخههای خنک کننده، چرخههای ترکیبی و بسیاری از دیگر موارد را میدهد.
روالهای روشهای بهینهسازی در متلب نوشته شدهاند و الگوریتم مورد استفاده با IPSEpro® به منظور حل مسئله ترمودیناکی و انجام بهینهسازی یکپارچه شده است. برای انجام بهینهسازی، محدودیتها برای متغیرهای مسئله به صورتی مقرر شدهاند که در جدول زیر مشخص شده است.

محدودیتهای متغیرها در جدول زیر، نتایج حاصل شده برای متغیرها در هر روش و مقدار تابع هدف ارائه شده است. در شکلی که پس از جدول آمده است، نمودارهای تکامل تابع هزینه در رابطه با فراخوانی تابع برای بهینهسازی انجام شده، ارائه شده است.
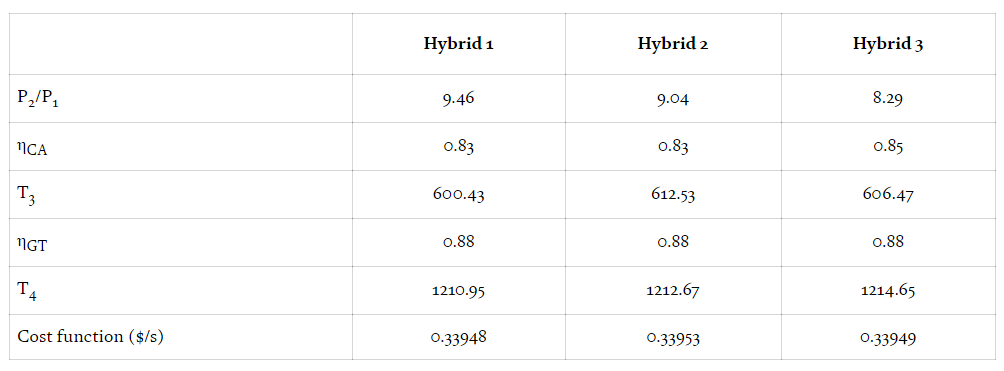
محدودیت متغیرها نتایج بهینهسازی در نمودارهای زیر ارائه شده است.
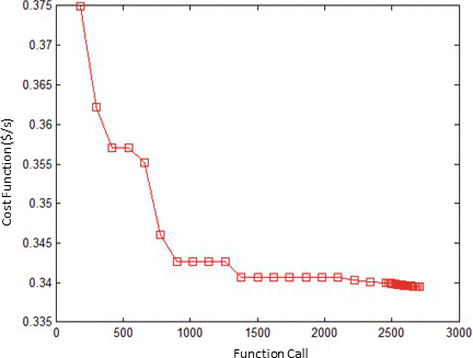
بهینهسازی ترکیبی ۱ 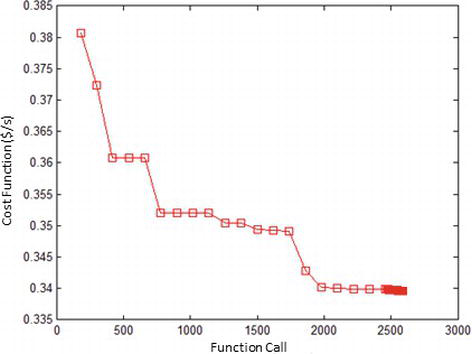
بهینهسازی ترکیبی ۲ 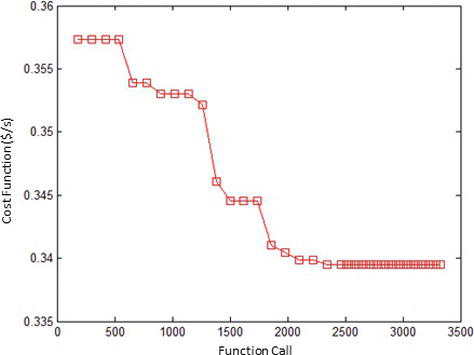
بهینهسازی ترکیبی ۳ پیادهسازی الگوریتم بهینه سازی ازدحام ذرات در پایتون
همانطور که پیش از این بیان شد، اساس الگوریتم ازدحام ذرات یا الگوریتم PSO بر این موضوع بنا شده است که با هم کار کردن برای رسیدن به هدف، موثرتر از کار نکردن به صورت تیمی است. در الگوریتم PSO این رفتار اجتماعی با به اشتراکگذاری اطلاعات بین یک مجموعه از راه حلهای ممکن که هر یک «ذره» (Particle) نامیده میشوند، انجام شده است.
یک ذره (چنانکه پیش از این نیز اشاره شد) به صورت زیر تعریف میشود:
به اشتراکگذاری اطلاعات در الگوریتم ازدحام ذرات محلی و الگوریتم ازدحام ذرات سراسری به دو صورت مختلف انجام میشود که در ادامه بیان شدهاند.
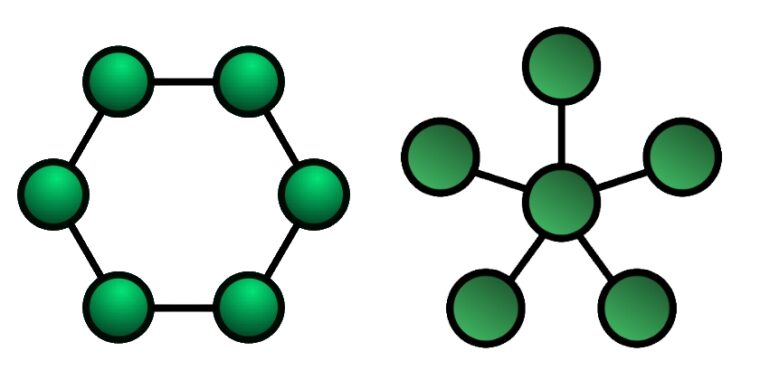
الگوریتم PSO سراسری (سمت چپ) و محلی (سمت راست) در انیمیشن زیر ساز و کار الگوریتم بهینه سازی ازدحام ذرات یا الگوریتم PSO قابل مشاهده است.
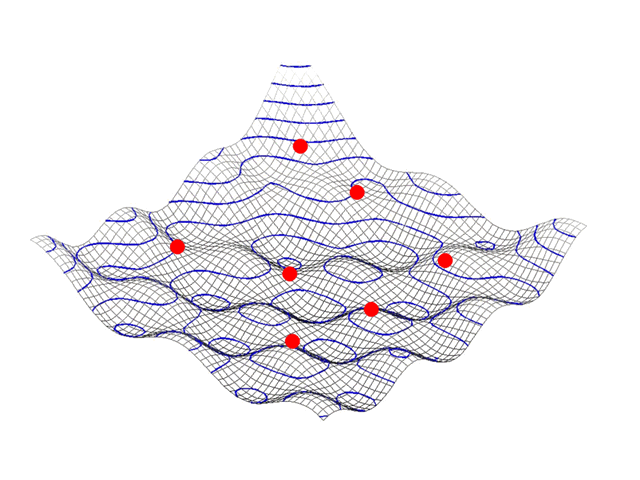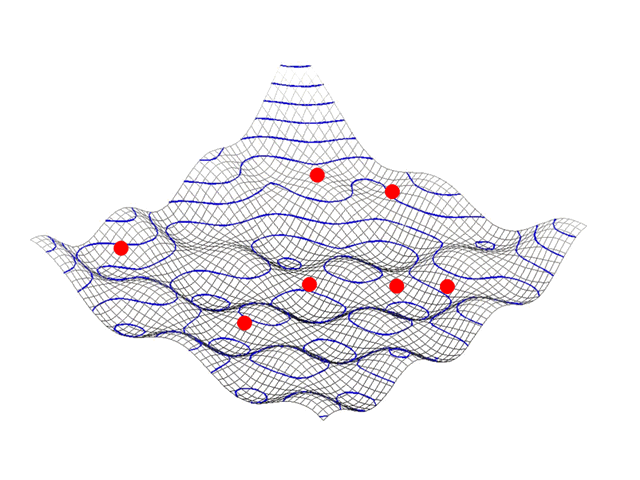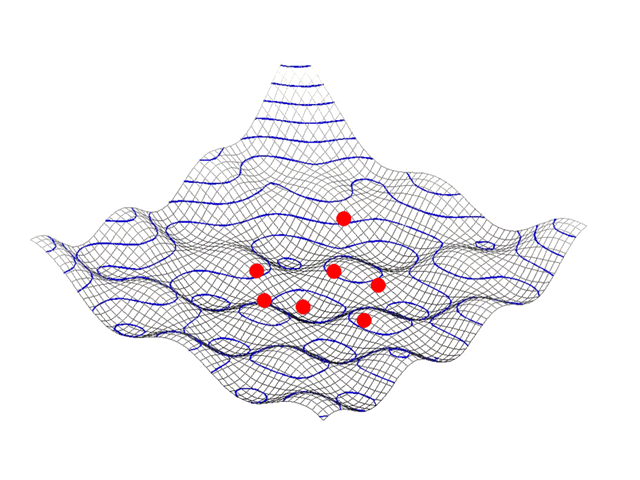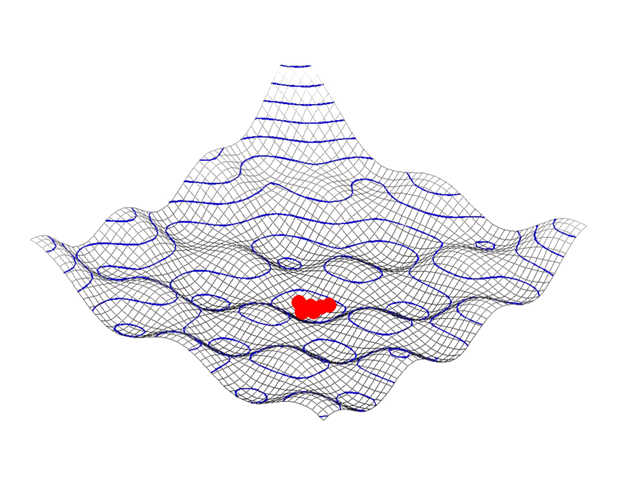
در الگوریتم PSO همانطور که پیش از این نیز بیان شد، کار با اولیهسازی یک جمعیت از ذرات در فضای جستجو انجام میشود. سپس، از طریق تکرارهای گوناگون، هر ذره به سمت بهترین راه حل حرکت میکند و این کار را با دنبال کردن بهترین راه حل سراسری در هر تکرار یا راه حل محلی شناخته شده در میان همسایگان آن بر اساس آنکه الگوریتم PSO محلی است یا سراسری، انجام میدهد.
در ادامه، شبه کد الگوریتم PSO سراسری آمده است.
For each particle Randomly initialize its position and velocity END Do For each particle Calculate its fitness value (measure of success) If the fitness value is better than the best fitness value (pBest) in history Set current value as the new pBest END Choose the particle with the best fitness value of all the particles as the gBest For each particle Calculate particle velocity Update particle position using the computed velocity End While maximum iterations or minimum error criteria is not attainedنقاطی که در اینجا باید مورد بررسی قرار بگیرند، مقداردهی اولیه ذرات و به روز رسانیهای آنها هم برای مکان و هم سرعت است.
برخی از نکاتی که باید پیرامون پیاده سازی الگوریتم بهینه سازی ازدحام ذرات در پایتون به آنها توجه داشت در ادامه بیان شدهاند.
کد الگوریتم بهینهسازی ازدحام ذرات در متلب
در ادامه، یک پیادهسازی ساده از الگوریتم بهینهسازی ازدحام ذرات در متلب نیز ارائه شده است.
Main
ObjectiveFunction
PSO
کد الگوریتم بهینه سازی ازدحام ذرات در جاوا
در ادامه، کد الگوریتم PSO در جاوا انجام شده است.
نتیجهگیری
در مطلب «الگوریتم بهینه سازی ازدحام ذرات | کد الگوریتم PSO در پایتون ، متلب و جاوا | راهنمای جامع»، مباحث پایهای روش PSO بیان، الگوریتم PSO تشریح و مزایا و معایب این روش مورد بررسی قرار گرفت. همچنین، روشهای ترکیبی با الگوریتم PSO که در واقع ترکیبی از روشهای قطعی و هیوریستیک هستند نیز به منظور بررسی مزایا و معایب آنها مورد بررسی قرار گرفتند. سپس، مثالهایی پیرامون الگوریتم PSO ارائه و پیادهسازی الگوریتم ازدحام ذرات در زبانهای برنامهنویسی پایتون، متلب و جاوا انجام شد.
چنانکه پیش از این نیز اشاره شد، درست نیست که گفته شود نتایج به دست آمده به وسیله یک الگوریتم بهینهسازی مثل PSO، بیشینه یا کمینه محلی است؛ بنابراین، بسیاری از پژوهشگران میگویند که این نتایج نزدیکترین مقدار به بیشینه یا کمینه محلی است. بنابراین، برخی از استراتژیها را به منظور تایید اعتبار نتایج بهینه به دست آمده با الگوریتم بهینه سازی ازدحام ذرات میتوان به کار گرفت.
یکی از این استراتژیها، مقایسه نتایج به دست آمده به وسیله دیگر الگوریتمهای بهینهسازی است. در غیاب دادههای بهینه در دسترس، به دلیل محدودیتهای محاسباتی و یا حتی فقدان نتایج یک موضوع، این امکان وجود دارد که به عنوان استراتژی، مقایسه اطلاعات از مدلهای فیزیکی واقعی انجام شود که از طریق الگوریتمهای بهینهسازی قابل حصول نیستند. ولیکن منجر به فعالیتهای مهندسی خوب و مقایسه نتایج از طریق تجربیات فنی میشوند. همچنین، این امکان وجود دارد که الگوریتم PSO روی مسائل مهندسی گوناگون اعمال شود که در مطلب «الگوریتم بهینه سازی ازدحام ذرات | کد الگوریتم PSO در پایتون ، متلب و جاوا | راهنمای جامع» نمونههایی از آن مورد بررسی قرار گرفت.
- برای هر i در جمعیت ازدحام با اندازه p:













با سلام و احترام خدمت خانم مهندس حصارکی
و تشکر از مطالب بسیار خوب و مفید شما
سپاسگزارم موفق باشید