در ریاضیات، درون یابی دو خطی (Bilinear Interpolation) تعمیمی از درونیابی خطی برای درونیابی توابع دو متغیره (به عنوان مثال، تابعی از x و y) در یک شبکه دو بُعدی افقی-عمودی است. درون یابی دو خطی با استفاده از درونیابی خطی ابتدا در یک جهت و سپس به کار گیری آن در جهت دیگر انجام میشود. اگرچه هر مرحله الگوریتم درون یابی دو خطی خطی است، اما پاسخ نهایی به دست آمده دیگر خطی نیست و میتوان گفت که درجه دوم است. درون یابی دو خطی یکی از تکنیکهای اساسی «بازنمونهگیری» (Resampling) در بینایی ماشین و پردازش تصویر است.
الگوریتم درون یابی دو خطی
فرض کنید میخواهیم مقدار تابع مجهول f f f ( x , y ) ( x , y ) ( x , y ) f f f Q 11 = ( x 1 , y 1 ) Q _ {11} = ( x_1 , y _ 1 ) Q 11 = ( x 1 , y 1 ) Q 12 = ( x 1 , y 2 ) Q _ { 1 2} = ( x _ 1 , y _ 2 ) Q 12 = ( x 1 , y 2 ) Q 21 = ( x 2 , y 1 ) Q _ { 21} = ( x _ 2 , y _ 1 ) Q 21 = ( x 2 , y 1 ) Q 22 = ( x 2 , y 2 ) Q _ { 22} = ( x _ 2 , y _ 2 ) Q 22 = ( x 2 , y 2 )
ابتدا درونیابی خطی را برای x x x
f ( x , y 1 ) ≈ x 2 − x x 2 − x 1 f ( Q 11 ) + x − x 1 x 2 − x 1 f ( Q 21 ) , f ( x , y 2 ) ≈ x 2 − x x 2 − x 1 f ( Q 12 ) + x − x 1 x 2 − x 1 f ( Q 22 ) . \begin {align}
f ( x , y _ 1 ) & \approx \frac { x _ 2 - x } { x _ 2 - x _ 1 } f ( Q _ { 1 1 } ) + \frac { x - x _ 1 } { x _ 2 - x _ 1 } f ( Q _ { 2 1 } ) , \\
f ( x , y _ 2 ) & \approx \frac { x _ 2 - x } { x _ 2 - x _ 1 } f ( Q _ { 1 2 } ) + \frac { x - x _ 1 } { x _ 2 - x _ 1 } f ( Q _ { 2 2 } ) .
\end {align} f ( x , y 1 ) f ( x , y 2 ) ≈ x 2 − x 1 x 2 − x f ( Q 11 ) + x 2 − x 1 x − x 1 f ( Q 21 ) , ≈ x 2 − x 1 x 2 − x f ( Q 12 ) + x 2 − x 1 x − x 1 f ( Q 22 ) .
در ادامه، درونیابی را برای y y y
f ( x , y ) ≈ y 2 – y y 2 – y 1 f ( x , y 1 ) + y – y 1 y 2 – y 1 f ( x , y 2 ) = y 2 – y y 2 – y 1 ( x 2 − x x 2 – x 1 f ( Q 11 ) + x – x 1 x 2 – x 1 f ( Q 21 ) ) + y – y 1 y 2 – y 1 ( x 2 – x x 2 – x 1 f ( Q 12 ) + x – x 1 x 2 – x 1 f ( Q 22 ) ) = 1 ( x 2 – x 1 ) ( y 2 – y 1 ) ( f ( Q 11 ) ( x 2 – x ) ( y 2 – y ) + f ( Q 21 ) ( x – x 1 ) ( y 2 – y ) + f ( Q 12 ) ( x 2 – x ) ( y − y 1 ) + f ( Q 22 ) ( x – x 1 ) ( y − y 1 ) ) = 1 ( x 2 – x 1 ) ( y 2 – y 1 ) [ x 2 – x x – x 1 ] [ f ( Q 11 ) f ( Q 12 ) f ( Q 21 ) f ( Q 22 ) ] [ y 2 – y y – y 1 ] . \begin {align}
f ( x , y ) & \approx \frac { y _ 2 – y } { y _ 2 – y _ 1 } f ( x , y _ 1 ) + \frac { y – y _ 1 } { y _ 2 – y _ 1 } f ( x , y _ 2 ) \\
& = \frac { y _ 2 – y } { y _ 2 – y _ 1 } \left ( \frac { x _ 2 -x } { x _ 2 – x _ 1 } f ( Q _ { 1 1 } ) + \frac { x – x _ 1 } { x _ 2 – x _ 1 } f ( Q _ { 2 1 } ) \right ) + \frac { y – y _ 1 } { y _ 2 – y _ 1 } \left ( \frac { x _ 2 – x } { x _ 2 – x _ 1 } f ( Q _ { 1 2 } ) + \frac { x – x _ 1 } { x _ 2 – x _ 1 } f ( Q _ { 2 2 } ) \right ) \\
& = \frac { 1 } { ( x _ 2 – x _ 1 ) ( y _ 2 – y _ 1 ) } \big ( f ( Q _ { 1 1 } ) ( x _ 2 – x ) ( y _ 2 – y ) + f ( Q _ { 2 1 } ) ( x – x _ 1 ) ( y _ 2 – y ) \\ & \quad \;+ f ( Q _ { 1 2 } ) ( x _ 2 – x ) ( y -y _ 1 ) + f ( Q _ { 2 2 } ) ( x – x _ 1 ) ( y- y _1 ) \big ) \\
& = \frac { 1 } { ( x _ 2 – x _ 1 ) ( y _ 2 – y _ 1 ) } \begin {bmatrix} x _ 2 – x & x – x _ 1 \end {bmatrix} \begin {bmatrix} f ( Q _ { 1 1 } ) & f ( Q _ { 1 2 } ) \\ f ( Q _ { 2 1 } ) & f ( Q _ { 2 2 } ) \end {bmatrix} \begin {bmatrix}
y _ 2 – y \\ y – y _ 1 \end {bmatrix} .
\end {align} f ( x , y ) ≈ y 2 – y 1 y 2 – y f ( x , y 1 ) + y 2 – y 1 y – y 1 f ( x , y 2 ) = y 2 – y 1 y 2 – y ( x 2 – x 1 x 2 − x f ( Q 11 ) + x 2 – x 1 x – x 1 f ( Q 21 ) ) + y 2 – y 1 y – y 1 ( x 2 – x 1 x 2 – x f ( Q 12 ) + x 2 – x 1 x – x 1 f ( Q 22 ) ) = ( x 2 – x 1 ) ( y 2 – y 1 ) 1 ( f ( Q 11 ) ( x 2 – x ) ( y 2 – y ) + f ( Q 21 ) ( x – x 1 ) ( y 2 – y ) + f ( Q 12 ) ( x 2 – x ) ( y − y 1 ) + f ( Q 22 ) ( x – x 1 ) ( y − y 1 ) ) = ( x 2 – x 1 ) ( y 2 – y 1 ) 1 [ x 2 – x x – x 1 ] [ f ( Q 11 ) f ( Q 21 ) f ( Q 12 ) f ( Q 22 ) ] [ y 2 – y y – y 1 ] .
توجه کنید که اگر ابتدا درونیابی را برای y y y x x x
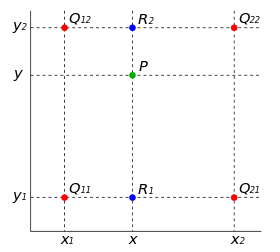
شکل زیر، نمای بصری روش درون یابی دو خطی را نشان میدهد. در این شکل، چهار نقطه قرمز، نقاط داده هستند و نقطه سبز نقطه مورد نظر برای درونیابی است.
یک روش دیگر برای درون یابی دو خطی
یک روش دیگر برای یافتن جواب درون یابی دو خطی به صورت زیر است:
f ( x , y ) ≈ a 0 + a 1 x + a 2 y + a 3 x y f ( x , y ) \approx a _ 0 + a _ 1 x + a _ 2 y + a _ 3 x y f ( x , y ) ≈ a 0 + a 1 x + a 2 y + a 3 x y
که در آن، ضرایب از حل دستگاه زیر به دست میآیند:
[ 1 x 1 y 1 x 1 y 1 1 x 1 y 2 x 1 y 2 1 x 2 y 1 x 2 y 1 1 x 2 y 2 x 2 y 2 ] [ a 0 a 1 a 2 a 3 ] = [ f ( Q 11 ) f ( Q 12 ) f ( Q 21 ) f ( Q 22 ) ] \begin {align}
\begin {bmatrix}
1 & x _ 1 & y _ 1 & x _ 1 y _ 1 \\
1 & x _ 1 & y _ 2 & x _ 1 y _ 2 \\
1 & x _ 2 & y _ 1 & x _ 2 y _ 1 \\
1 & x _ 2 & y _ 2 & x _ 2 y _ 2
\end {bmatrix} \begin {bmatrix}
a _ 0 \\ a _ 1 \\ a _ 2 \\ a _ 3
\end {bmatrix} = \begin {bmatrix}
f ( Q _ { 1 1 } ) \\ f ( Q _ { 1 2 } ) \\ f ( Q _ { 2 1 } ) \\ f ( Q _ { 2 2 } )
\end {bmatrix}
\end {align} 1 1 1 1 x 1 x 1 x 2 x 2 y 1 y 2 y 1 y 2 x 1 y 1 x 1 y 2 x 2 y 1 x 2 y 2 a 0 a 1 a 2 a 3 = f ( Q 11 ) f ( Q 12 ) f ( Q 21 ) f ( Q 22 )
این ضرایب به صورت زیر هستند:
a 0 = f ( Q 11 ) x 2 y 2 ( x 1 − x 2 ) ( y 1 − y 2 ) + f ( Q 12 ) x 2 y 1 ( x 1 − x 2 ) ( y 2 − y 1 ) + f ( Q 21 ) x 1 y 2 ( x 1 − x 2 ) ( y 2 − y 1 ) + f ( Q 22 ) x 1 y 1 ( x 1 − x 2 ) ( y 1 − y 2 ) , a _ 0 = \frac { f ( Q _ { 1 1 } ) x _ 2 y _ 2 } { ( x _ 1 - x _ 2 ) ( y _ 1 - y _ 2 ) } + \frac { f ( Q _ { 1 2 } ) x _ 2 y _ 1 }{ ( x _ 1 - x _ 2 ) ( y _ 2 - y _1 ) } + \frac { f ( Q _ { 2 1 } ) x _ 1 y _ 2 } { ( x _1 - x _ 2 ) ( y _ 2 - y _ 1 ) } + \frac { f ( Q _ { 2 2 } ) x _ 1 y _ 1 } { ( x _ 1 - x _ 2 ) ( y _ 1 - y _ 2 ) } , a 0 = ( x 1 − x 2 ) ( y 1 − y 2 ) f ( Q 11 ) x 2 y 2 + ( x 1 − x 2 ) ( y 2 − y 1 ) f ( Q 12 ) x 2 y 1 + ( x 1 − x 2 ) ( y 2 − y 1 ) f ( Q 21 ) x 1 y 2 + ( x 1 − x 2 ) ( y 1 − y 2 ) f ( Q 22 ) x 1 y 1 ,
a 1 = f ( Q 11 ) y 2 ( x 1 − x 2 ) ( y 2 − y 1 ) + f ( Q 12 ) y 1 ( x 1 − x 2 ) ( y 1 − y 2 ) + f ( Q 21 ) y 2 ( x 1 − x 2 ) ( y 1 − y 2 ) + f ( Q 22 ) y 1 ( x 1 − x 2 ) ( y 2 − y 1 ) , a _ 1 = \frac { f ( Q _ { 1 1 } ) y _ 2 } { ( x _ 1 - x _ 2 ) ( y _ 2 - y _ 1 ) } + \frac { f ( Q _ { 1 2 } ) y _ 1 } { ( x _ 1 - x _ 2 ) ( y _ 1 - y _ 2 ) } + \frac { f ( Q _ { 2 1 } ) y _ 2 } { ( x _ 1 - x _ 2 ) ( y _ 1 - y _ 2 ) } + \frac { f ( Q _ { 2 2 } ) y _ 1 } { ( x _ 1 - x _ 2 ) ( y _ 2 - y _ 1 ) } , a 1 = ( x 1 − x 2 ) ( y 2 − y 1 ) f ( Q 11 ) y 2 + ( x 1 − x 2 ) ( y 1 − y 2 ) f ( Q 12 ) y 1 + ( x 1 − x 2 ) ( y 1 − y 2 ) f ( Q 21 ) y 2 + ( x 1 − x 2 ) ( y 2 − y 1 ) f ( Q 22 ) y 1 ,
a 2 = f ( Q 11 ) x 2 ( x 1 − x 2 ) ( y 2 − y 1 ) + f ( Q 12 ) x 2 ( x 1 − x 2 ) ( y 1 − y 2 ) + f ( Q 21 ) x 1 ( x 1 − x 2 ) ( y 1 − y 2 ) + f ( Q 22 ) x 1 ( x 1 − x 2 ) ( y 2 − y 1 ) , a _ 2 = \frac { f ( Q _ { 1 1 } ) x _ 2 } { ( x _ 1 - x _ 2 ) ( y _ 2 - y _ 1 ) } + \frac { f ( Q _ { 1 2 } ) x _ 2 } { ( x _ 1 - x _ 2 ) ( y _ 1 - y _ 2 ) } + \frac { f ( Q _ { 2 1} ) x _ 1 } { ( x _ 1 - x _ 2 ) ( y _ 1 - y _ 2 ) } + \frac { f ( Q _ { 2 2 } ) x _ 1 } { ( x _ 1 - x _ 2 ) ( y _ 2 - y _ 1 ) } , a 2 = ( x 1 − x 2 ) ( y 2 − y 1 ) f ( Q 11 ) x 2 + ( x 1 − x 2 ) ( y 1 − y 2 ) f ( Q 12 ) x 2 + ( x 1 − x 2 ) ( y 1 − y 2 ) f ( Q 21 ) x 1 + ( x 1 − x 2 ) ( y 2 − y 1 ) f ( Q 22 ) x 1 ,
اگر بخواهیم جواب را برحسب f ( Q ) f ( Q ) f ( Q )
f ( x , y ) ≈ b 11 f ( Q 11 ) + b 12 f ( Q 12 ) + b 21 f ( Q 21 ) + b 22 f ( Q 22 ) f ( x , y ) \approx b _ { 1 1 } f ( Q _ { 1 1 } ) + b _ { 1 2 } f ( Q _ { 1 2 } ) + b _ { 2 1 } f ( Q _ { 2 1 } ) + b _ { 2 2 } f ( Q _ { 2 2 } ) f ( x , y ) ≈ b 11 f ( Q 11 ) + b 12 f ( Q 12 ) + b 21 f ( Q 21 ) + b 22 f ( Q 22 )
که در آن، ضرایب را میتوان به صورت زیر به دست آورد:
[ b 11 b 12 b 21 b 22 ] = ( [ 1 x 1 y 1 x 1 y 1 1 x 1 y 2 x 1 y 2 1 x 2 y 1 x 2 y 1 1 x 2 y 2 x 2 y 2 ] − 1 ) T [ 1 x y x y ] . \begin {bmatrix}
b _ { 1 1 } \\ b _ { 1 2 } \\ b _ { 2 1 } \\ b _ { 2 2 }
\end {bmatrix} =
\left ( \begin {bmatrix}
1 & x _ 1 & y _ 1 & x _ 1 y _ 1 \\
1 & x _ 1 & y _ 2 & x _ 1 y _ 2 \\
1 & x _ 2 & y _ 1 & x _ 2 y _ 1 \\
1 & x _ 2 & y _ 2 & x _ 2 y _ 2
\end {bmatrix} ^ { - 1 } \right ) ^ { \rm T } \begin {bmatrix}
1 \\ x \\ y \\ x y
\end {bmatrix} . b 11 b 12 b 21 b 22 = 1 1 1 1 x 1 x 1 x 2 x 2 y 1 y 2 y 1 y 2 x 1 y 1 x 1 y 2 x 2 y 1 x 2 y 2 − 1 T 1 x y x y .
درون یابی دو خطی مربع واحد
اگر دستگاه مختصاتی را انتخاب کنیم که چهار نقطه f f f ( 0 , 0 ) ( 0 , 0 ) ( 0 , 0 ) ( 1 , 0 ) ( 1 , 0 ) ( 1 , 0 ) ( 0 , 1 ) ( 0 , 1 ) ( 0 , 1 ) ( 1 , 1 ) ( 1 , 1 ) ( 1 , 1 )
f ( x , y ) ≈ f ( 0 , 0 ) ( 1 − x ) ( 1 − y ) + f ( 1 , 0 ) x ( 1 − y ) + f ( 0 , 1 ) ( 1 − x ) y + f ( 1 , 1 ) x y f ( x , y ) \approx f ( 0 , 0 ) ( 1 - x ) ( 1 - y ) + f ( 1 , 0 ) x ( 1 - y ) + f ( 0 , 1 ) ( 1 - x ) y + f ( 1 , 1 ) x y f ( x , y ) ≈ f ( 0 , 0 ) ( 1 − x ) ( 1 − y ) + f ( 1 , 0 ) x ( 1 − y ) + f ( 0 , 1 ) ( 1 − x ) y + f ( 1 , 1 ) x y
یا به طور معادل به صورت ماتریسی داریم:
f ( x , y ) ≈ [ 1 − x x ] [ f ( 0 , 0 ) f ( 0 , 1 ) f ( 1 , 0 ) f ( 1 , 1 ) ] [ 1 − y y ] . f ( x , y ) \approx \begin {bmatrix} 1 - x & x \end {bmatrix} \begin {bmatrix} f ( 0 , 0 ) & f ( 0 , 1 ) \\ f ( 1 , 0 ) & f ( 1 , 1 ) \end {bmatrix} \begin {bmatrix}
1 - y \\ y \end {bmatrix} . f ( x , y ) ≈ [ 1 − x x ] [ f ( 0 , 0 ) f ( 1 , 0 ) f ( 0 , 1 ) f ( 1 , 1 ) ] [ 1 − y y ] .
درون یابی دو خطی غیرخطی
همانگونه که از نام آن پیداست، درون یابی دو خطی خطی نیست و ضرب دو تابع خطی است. برای مثال، درون یابی دو خطی بالا که به دست آمد، دارای ضرب مقادیر x x x y y y
همچنین، درونیابی در مربع واحد را میتوان به صورت زیر نوشت:
f ( x , y ) = ∑ i = 0 1 ∑ j = 0 1 a i j x i y j = a 00 + a 10 x + a 01 y + a 11 x y f ( x , y ) = \sum _ { i = 0 } ^ 1 \sum _ { j = 0 } ^ 1 a _ { i j } x ^ i y ^ j = a _ { 0 0 } + a _ { 1 0 } x + a _ { 0 1 } y + a _ { 1 1 } x y f ( x , y ) = i = 0 ∑ 1 j = 0 ∑ 1 a ij x i y j = a 00 + a 10 x + a 01 y + a 11 x y
که در آن:
a 00 = f ( 0 , 0 ) , a 10 = f ( 1 , 0 ) − f ( 0 , 0 ) , a 01 = f ( 0 , 1 ) − f ( 0 , 0 ) , a 11 = f ( 1 , 1 ) + f ( 0 , 0 ) − ( f ( 1 , 0 ) + f ( 0 , 1 ) ) . \begin {align*} a _ { 0 0 } & = f ( 0 , 0 ) ,
\\ a _ { 1 0 } & = f ( 1 , 0 ) - f ( 0 , 0 ) ,
\\ a _ { 0 1 } & = f ( 0 , 1 ) - f ( 0 , 0 ) ,
\\ a _ { 1 1 } & = f ( 1 , 1 ) + f ( 0 , 0 ) -\big ( f ( 1 , 0 ) + f ( 0 , 1 ) \big ) . \end {align*} a 00 a 10 a 01 a 11 = f ( 0 , 0 ) , = f ( 1 , 0 ) − f ( 0 , 0 ) , = f ( 0 , 1 ) − f ( 0 , 0 ) , = f ( 1 , 1 ) + f ( 0 , 0 ) − ( f ( 1 , 0 ) + f ( 0 , 1 ) ) .
نتیجه درون یابی دو خطی مستقل از آن محوری است که اول یا دوم درونیابی میشود. اگر در ابتدا درونیابی خطی در جهت y y y x x x
اگر این مطلب برایتان مفید بوده است، آموزشهای زیر نیز به شما پیشنهاد میشوند:
^^














با سلام، خواهشمند است بفرمایید برای درونیابی دو بعدی در اکسل راه حل چیست؟ آیا تابعی وجود دارد؟