حل معادله حالت – از صفر تا صد
حل معادله حالت (استفاده از فرم فضای حالت) یکی از روشهای معروف برای حل معادلات دیفرانسیل است. در این فضا یک معادله دیفرانسیل مرتبه n، به صورت n معادله مرتبه اول مستقل بیان میشود. مزیت استفاده از فرم فضای حالت سادگی حل معادله دیفرانسیل و پیادهسازی راحت در کامپیوترهای دیجیتال است. در این مطلب به بیان چگونگی حل معادلات دیفرانسیل و معادلات تفاضلی (گسسته) پرداخته میشود.
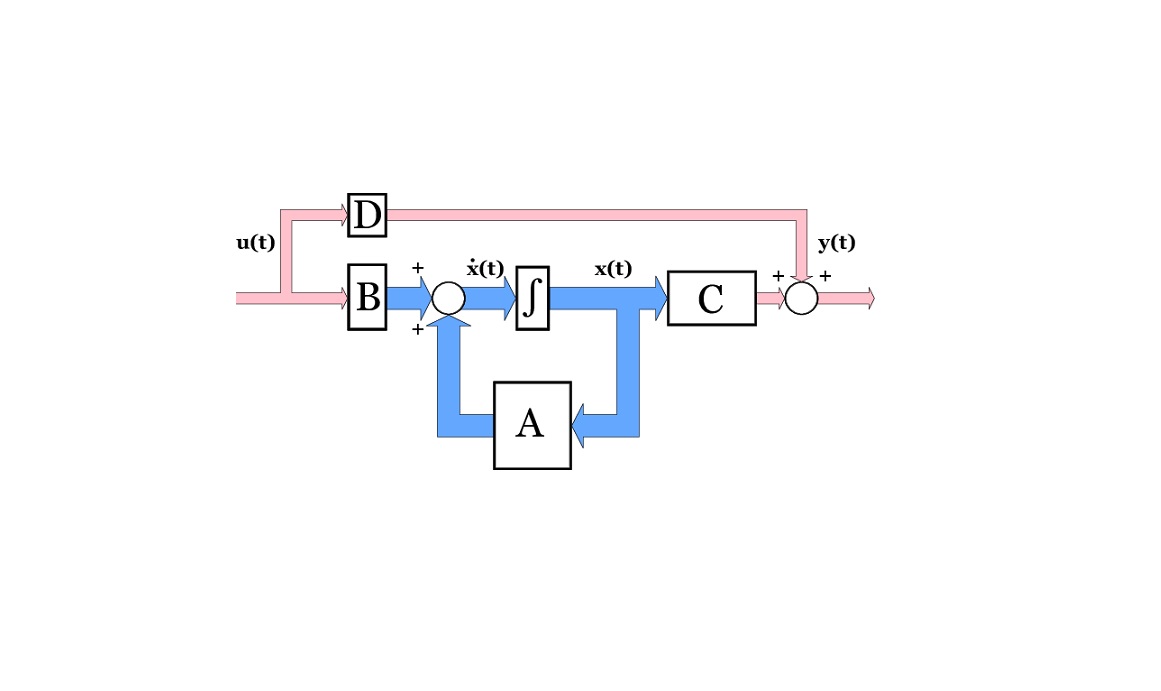
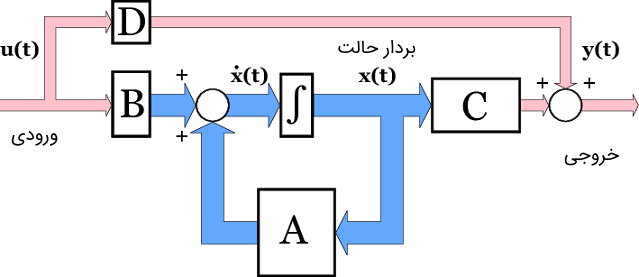
حل معادله حالت برای سیستمهای پیوسته در زمان
در حالت کلی سیستمهای دینامیکی به صورت زیر مدلسازی میشوند:
در مورد سیستمهای خطی نامتغیر با زمان، این معادله را میتوان به صورت زیر بازنویسی کرد:
حال هدف این است که معادلات سیستم بالا را حل کنیم تا یک فرم بسته (Closed Form) به صورت تابعی از متغیرهای بردار حالت و بردار اندازهگیری به دست آوریم.
حالت برای تمام زمانهای
برای حل معادله حالت ابتدا حالت سادهای که برای تمام زمانهای ، است را در نظر میگیریم. در این مورد معادلات حالت به فرم زیر بازنویسی میشوند:
از معادلات دیفرانسیل پایه میدانیم که برای یک اسکالر، حل برابر با است. اگر بردار و ماتریس باشند، حلی مشابه به صورت زیر به دست میآید:
توجه کنید که چون یک ماتریس است، نیاز داریم که توان آن را به صورت زیر تعریف کنیم:
اگر حالت در لحظه مشخص باشد، آنگاه حل برابر است با:
اگر ماتریس را بتوان به صورت نوشت، آنگاه این ماتریس دارای بردارهای ویژه (Eigen Vector) خطی و مستقل است. در این حالت جواب را میتوان به صورت زیر نوشت:
با جایگذاری در معادله بالا داریم:
در معادله بالا ماتریسی است که المانهای خارج از قطر اصلی آن صفر هستند و المان روی قطر برابر با است. اگر قسمت حقیقی مقادیر ویژه ماتریس منفی باشد، در این صورت است، در غیر این صورت . این مشخصه در طراحی سیستمهای کنترل بسیار ضروری است. زیرا در یک سیستم کنترلی، قانون کنترلی (Control Law) به نحوی تعیین میشود که مقادیر ویژه اصلاح شده دینامیک سیستم دارای قسمت حقیقی منفی باشند.
حل عمومی
در این قسمت به دنبال یافتن پاسخ خاص برای معادله کلی به فرم خواهیم بود. با جایگذاری و بسط آن داریم:
پس از سادهسازی معادله به صورت زیر خواهد بود:
از معادله بالا نسبت به زمان انتگرال میگیریم:
بنابراین حل معادله برابر است با:
توجه کنید که است.
در نتیجه پاسخ معادله دیفرانسیل در فضای حالت برابر است با:
در حالتی که مقدار در نقطه مشخص باشد، داریم:
این پاسخ دارای مشخصههای زیر است:
- پاسخ فقط به سیگنال کنترلی در بازه 0 (یا ) و لحظه حال () بستگی خواهد داشت.
- این قانون که اگر (یا ) محدود باشد، محدود خواهد بود، دیگر صادق نیست، زیرا پاسخ به و نیز سیگنال کنترل بستگی دارد.
حل معادله حالت برای سیستمهای گسسته در زمان
دینامیک سیستمهای گسسته در زمان به صورت کلی توسط معادله زیر توصیف میشوند:
برای سیستمهای خطی تغییرناپذیر با زمان، این معادلات را میتوان به صورت زیر نوشت:
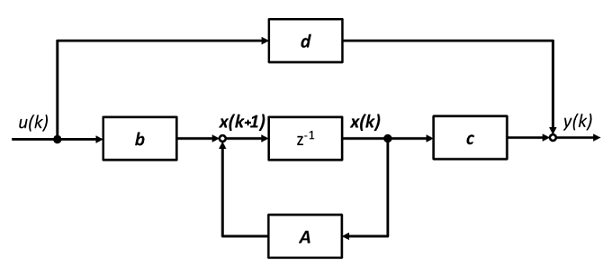
زمانی که باشد، دینامیک سیستم به صورت زیر است:
به سادگی میتوان نشان داد که پاسخ در این حالت برابر است با:
با جایگذاری داریم:
اگر اندازه تمام مقادیر ویژه ماتریس کمتر از یک باشد، آنگاه به سمت صفر همگرا خواهد شد، در غیر این صورت به میل میکند.
نکته: در مورد سیستمهای پیوسته در زمان، این شرط برقرار است که اگر مقادیر ویژه منفی باشند، پاسخ به سمت صفر همگرا میشود. اما در سیستم گسسته اگر اندازه مقدار ویژه کمتر از یک باشد، این حالت اتفاق میافتد. در واقع هر دو شرط معادل یکدیگر هستند.
حل بازگشتی
برای حل معادله حالت به صورت بازگشتی، معادله در لحظه اول را به دست میآوریم:
حال معادله برای لحظه دوم برابر است با:
با جایگذاری معادله به دست آمده برای لحظه اول در معادله لحظه دوم داریم:
به طریق مشابه، برای داریم:
بر اساس روند معادلات بالا برای جواب زیر استنتاج میشود:
حال با توجه به ، مقدار برابر است با:
مقدار به دست آمده را در معادله بالا جایگذاری میکنیم:
چون معادله پس از جایگذاری با فرمی مشابه با دارد، در نتیجه پاسخ به صورت زیر خواهد بود:
این پاسخ دارای مشخصههای زیر است:
- پاسخ برای فقط به سیگنال کنترلی در بازه 0 تا لحظه حال (k) بستگی دارد.
- این قانون که اگر محدود باشد، محدود است، دیگر صادق نخواهد بود، زیرا پاسخ به و نیز سیگنال کنترل بستگی دارد.
ارتباط بین نمایش پیوسته و گسسته در زمان
در معادلات بالا برای حل معادله حالت، با سیستمهای پیوسته و گسسته در زمان به نحوی متفاوت برخورد کردیم. اما یک سیستم پیوسته در زمان را میتوان به فرم گسسته در زمان نیز نوشت.
معادله سیستم پیوسته در زمان زیر را در نظر بگیرید:
مشتق تقریبا به صورت زیر است:
که در آن یک مقدار کوچک برای گسستهسازی سیستم است. انتخاب مناسب برای طراحی یک قانون کنترلی مناسب و مطالعه سیستمهای دینامیکی توسط شبیهسازی بسیار ضروری است. هرچه کوچکتر باشد، جواب دارای دقت بیشتری خواهد بود، اما زمان شبیهسازی نیز افزایش خواهد یافت. در مقابل، مقدار بزرگتر منجر به افزایش سرعت شبیهسازی میشود، ولی نتایج با دقت کمتری به دست خواهد آمد. انتخاب مقدار صحیح برای جواب با دقت مناسب در زمان شبیهسازی منطقی را تضمین میکند. شبیهسازی یک سیستم دینامیکی در بخشهای مختلف مورد نیاز است. معمولا مقدار را برابر با 0٫001 ثانیه انتخاب می کنند. اما اگر سیستم به شدت غیرخطی باشد و یا میلیونها پارامتر داشته باشد (مثلا در شبکههای عصبی)، یک بسیار کوچکتر از مرتبه مورد نیاز است.
معادله دینامیکی سیستم به صورت زیر است:
توجه کنید که اگر تمام مقادیر ویژه دارای قسمت حقیقی منفی باشند، آنگاه قسمت حقیقی تمام مقادیر ویژه برای یک مقدار کوچک ، کمتر از 1 هستند و یا زمانی که به صفر همگرا میشوند.
جمعبندی
در این مطلب دیدیم که چگونه پاسخ معادلات دینامیکی سیستم نمایش داده شده در فرم فضای حالت، محاسبه میشود. همچنین به این نکته اشاره کردیم که اگر مقادیر ویژه در یک سیستم پیوسته در زمان دارای بخش حقیقی منفی باشند و یا در سیستم گسسته در زمان اندازه کمتر از 1 داشته باشند، زمانی که هیچ کنترلی اعمال نشود، حالت سیستم به سمت صفر میل خواهد کرد. این مشخصه بسیار ضروری است و برای طراحی قانون کنترلی به کار گرفته میشود. هرچند، قبل از طراحی قانون کنترلی باید از کنترلپذیری سیستم اطمینان حاصل کرد. به علاوه، چون قانون کنترلی تابعی از حالتهای تخمین زده شده است، این نکته نیز ضروری است که مشخص شود آیا تمام حالتها میتوانند تخمین زده شوند (روئیتپذیر باشند) یا خیر.
اگر مطالب بیان شده برای شما مفید بوده و علاقهمند به یادگیری مباحث مرتبط با آن هستید، پیشنهاد میکنیم به آموزشهای زیر مراجعه کنید:
- مجموعه آموزشهای مهندسی کنترل
- آموزش سیستمهای کنترل خطی
- مجموعه آموزشهای ریاضیات
- آموزش معادلات دیفرانسیل به همراه حل نمونه سئوالات آزمون کارشناسی ارشد
- معادله دیفرانسیل خطی — از صفر تا صد
- معادلات دیفرانسیل مرتبه اول — روشهای حل به زبان ساده
- معادلات دیفرانسیل مرتبه دوم — به زبان ساده
^^













خیلی عالی ممنون