معادله دیفرانسیل خطی — از صفر تا صد (+ دانلود فیلم آموزش رایگان)

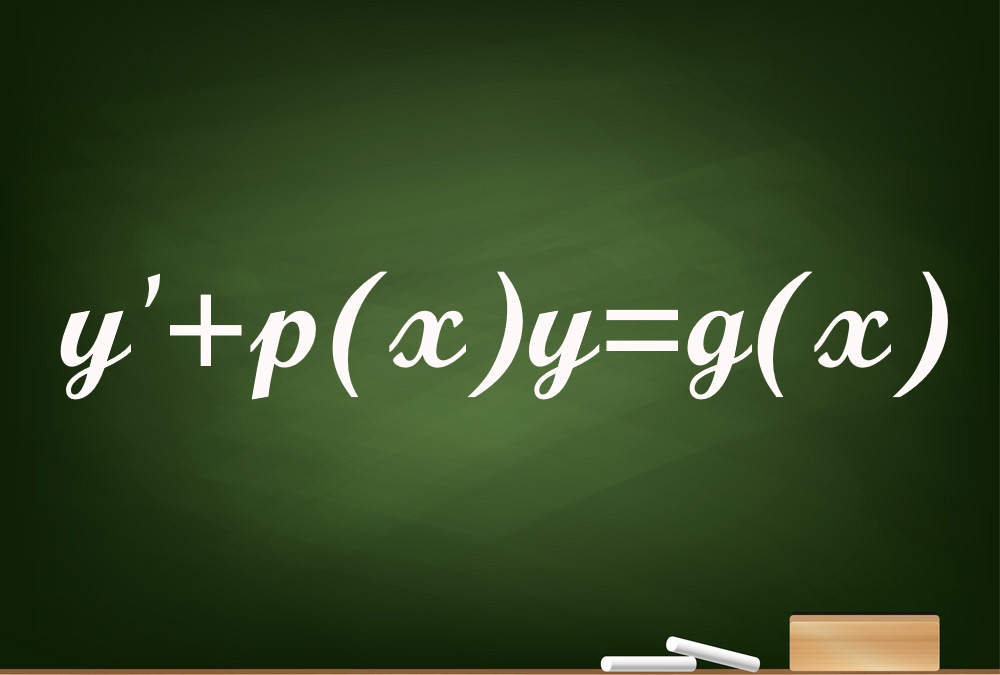
در راستای ارائه مفاهیم مرتبط با معادلات دیفرانسیل، روش‌های حل این معادلات اعم از مرتبه اول، دوم و مراتب بالاتر توضیح داده ‌شدند. با این حال در این مطلب قصد داریم تا معادله دیفرانسیل خطی مرتبه اول را مورد بررسی قرار دهیم. البته مطالعه مطالب معادلات دیفرانسیل، معادلات مرتبه دوم، معادلات دیفرانسیل مرتبه بالاتر و معادلات ناهمگن نیز به منظور درک هرچه بهتر این مطلب، خالی از لطف نخواهد بود.

پاسخ معادله دیفرانسیل خطی

یک معادله دیفرانسیل مرتبه اول می‌تواند خطی یا غیر خطی باشد. همان‌طور که پیش‌تر نیز اشاره شده، اگر در یک معادله دیفرانسیل توابعِ y یا مشتقاتشان در هم ضرب شده باشند، آن معادله غیر خطی خواهد بود. برای نمونه رابطه زیر، یک معادله دیفرانسیل غیرخطی را نشان می‌دهد.

$$\large {y ^ { \prime }} ^ 2 + y + x ^ 2 + 1 = 0$$

فیلم آموزش معادلات دیفرانسیل با رویکرد حل مساله و تست کنکور ارشد در فرادرس

کلیک کنید

دلیل غیر خطی بودن رابطه فوق وجود ترمِ $$\large {y ^ { \prime } } ^ 2$$ است. در این مطلب قصد داریم تا معادلات دیفرانسیل خطی مرتبه اول را حل کنیم. شکل کلی این معادلات به صورت زیر است.

$$\large \begin {equation} \frac { { d y } } { { d t } } + p \left ( t \right ) y = g \left ( t \right ) \end {equation}$$
رابطه ۱

توجه داشته باشید که در رابطه فوق، هر دو تابع (p(t و (g(t پیوسته هستند.

پاسخ معادله دیفرانسیل خطی

به منظور بدست آوردن پاسخ معادله ۱، طرفین آن را در تابعی جادویی - که فعلا آن را نمی‌شناسیم - ضرب می‌کنیم. با فرض این که اسم این تابع $$\mu ( t )$$ باشد، به معادله زیر می‌رسیم. البته در ادامه این تابع را عامل انتگرال‌ساز صدا خواهیم زد.

$$\large \begin {equation} \mu \left ( t \right ) \frac { { d y } } { { d t } } + \mu \left ( t \right ) p \left ( t \right ) y = \mu \left ( t \right ) g \left ( t \right ) \end {equation}$$

فرض کنید تابع $$\mu ( t )$$ به شکلی است که رابطه زیر برای آن برقرار است.

$$\large \begin {equation} \mu \left ( t \right ) p \left ( t \right ) = \mu ^ { \prime } \left ( t \right ) \end {equation}$$

در ادامه نحوه بدست آوردن $$\mu ( t )$$ را توضیح خواهیم داد. با در نظر گرفتن فرض فوق، رابطه زیر بدست می‌آید.

$$\large \begin {equation} \mu \left ( t \right ) \frac { { d y } } { { d t } } + \mu ^ { \prime } \left ( t \right ) y = \mu \left ( t \right ) g \left ( t \right ) \end {equation}$$
رابطه ۲

با استفاده از قوانین مشتق‌گیری می‌دانید که سمت چپ معادله بالا، برابر با مشتق حاصل‌ضرب $$\mu ( t ) y ( t )$$ است. بنابراین سمت چپ معادله برابر است با:

$$\large \mu \left ( t \right ) \frac { { d y } } { { d t } } + \mu ^ { \prime } \left ( t \right ) y = { \left ( { \mu \left ( t \right ) y \left ( t \right ) } \right ) ^ \prime }$$

با استفاده از رابطه فوق و رابطه ۲، عبارت زیر بدست می‌آید.

$$\large \begin {equation} { \left ( { \mu \left ( t \right ) y \left ( t \right ) } \right ) ^ \prime } = \mu \left ( t \right ) g \left ( t \right ) \end {equation}$$

حال به منظور بدست آوردن تابع y از طرفین رابطه فوق انتگرال می‌گیریم. با انجام این کار داریم:

$$\large \int { { { { \left ( { \mu \left ( t \right ) y \left ( t \right ) } \right ) } ^ \prime } \, d t } } = \int { { \mu \left ( t \right ) g \left ( t \right ) \, d t } }$$

$$\large \begin {equation} \mu \left ( t \right ) y \left ( t \right ) + c = \int { { \mu \left ( t \right ) g \left ( t \right ) \, d t } } \end {equation}$$

توجه داشته باشید که در هنگام انتگرال‌گیری ثابت c باید در نظر گرفته شود. در غیر این‌صورت به پاسخی اشتباه خواهیم رسید. با توجه به عبارت بدست آمده در بالا، تابع y به صورت زیر بدست می‌آید.

$$\large \begin {align*} \mu \left ( t \right ) y \left ( t \right ) & = \int { { \mu \left ( t \right ) g \left ( t \right ) \, d t } } - c \\ y \left ( t \right ) & = \frac { { \int { { \mu \left ( t \right ) g \left ( t \right ) \, d t } } - c } } { { \mu \left ( t \right ) } } \end {align*}$$

مقدار c- ناشناخته است، بنابراین می‌توان آن را به صورت ثابتی نامعلوم در نظر گرفت. نهایتا پاسخ یک معادله دیفرانسیل خطی مرتبه اول، برابر با عبارت زیر بدست می‌آید.

$$\large \boxed { \begin {equation} y \left ( t \right ) = \frac { { \int { { \mu \left ( t \right ) g \left ( t \right ) \, d t } } + c } } { { \mu \left ( t \right ) } } \end {equation} }$$
رابطه ۳

البته همان‌طور که می‌دانید مثبت یا منفی فرض کردن c، تاثیری در پاسخ نهایی نخواهد داشت.

بدست آوردن عامل انتگرال‌ساز ($$\large \mu ( t )$$)

در بالا متوجه شدیم که با ضرب یک معادله دیفرانسیل خطی مرتبه اول در تابعی جادویی تحت عنوان $$\mu ( t )$$ می‌توان پاسخ y را با استفاده از فرمولی کلی بر حسب آن بدست آورد.

فیلم آموزش معادلات دیفرانسیل با میپل Maple در فرادرس

کلیک کنید

حال سوال این است تابع $$\large \mu ( t )$$ به چه شکل بدست می‌آید؟ بدین منظور از فرض بیان شده در بالا استفاده می‌کنیم.

$$\large \mu \left ( t \right ) p \left ( t \right ) = \mu ^ { \prime } \left ( t \right )$$

با تقسیم کردن طرفین رابطه فوق به $$\mu ( t )$$ به رابطه زیر می‌رسیم.

$$\large \frac { { \mu ^ { \prime } \left ( t \right ) } } { { \mu \left ( t \right ) } } = p \left ( t \right )$$

سمت چپ رابطه بالا معادل با $$( \ln { \ {\mu (t)} } )'$$ است. بنابراین می‌توان رابطه فوق را به صورت زیر بازنویسی کرد.

$$\large { \left ( { \ln \mu \left ( t \right ) } \right ) ^ \prime } = p \left ( t \right )$$

با انتگرال‌گیری، رابطه زیر بدست می‌آید.

$$\large \begin {align*} \ln \mu \left ( t \right ) + k &= \int { { p \left ( t \right ) \, d t } } \\ \ln \mu \left ( t \right ) & = \int { { p \left ( t \right ) \, d t } } + k \end {align*}$$

با نوشتن طرفین رابطه فوق به صورت نمایی، تابع $$\mu ( t )$$ بدست خواهد آمد.

$$\large \mu \left ( t \right ) = { { \bf{e} } ^ { \int { { p \left ( t \right ) \, d t } } \, + \, k } }$$

با استفاده از قوانین لگاریتمی نهایتا تابع $$\mu ( t )$$ به صورت زیر بدست می‌آید.

$$\large \begin {equation} \mu \left ( t \right ) = k \, { { \bf { e } } ^ { \int { { p \left ( t \right ) \, d t } } } } \end {equation}$$

پاسخ نهایی معادله دیفرانسیل خطی

با بدست آمدن تابع $$\mu ( t )$$، پاسخ معادله نیز به صورت زیر بدست می‌آید.

$$\large \large \begin {align*} y \left ( t \right ) & = \frac { { \int { { k \, { { \bf{ e } } ^ { \int { { p \left ( t \right ) \, d t } } } } g \left ( t \right ) \, d t } } + c } } { { k \, { { \bf{e} } ^ { \int { { p \left( t \right ) \, d t } } } } } } \\~\\ & = \frac { { k \int { { \, { { \bf{e}} ^ { \int { { p \left ( t \right ) \, d t } } } } g \left ( t \right ) \, d t } } + c } } { { k \, { { \bf{e}} ^ { \int { { p \left ( t \right ) \, d t } } } } } } \\~\\ & = \frac { { \int { { \,{ { \bf{e}} ^ { \int { { p \left ( t \right ) \, d t } } } } g \left ( t \right ) \, d t } } + \frac { c } { k } } } { { \,{ { \bf{e}} ^ { \int { { p \left ( t \right)\, d t } } } } } } \end {align*}$$

فیلم آموزش معادلات دیفرانسیل + حل سوالات کنکور کارشناسی ارشد در فرادرس

کلیک کنید

با فرض کردن c/k به عنوان یک ثابت، نهایتا پاسخ معادله دیفرانسیل خطی مرتبه اول، به صورت زیر قابل بیان است.

$$\large \boxed { \begin {equation} y \left ( t \right ) = \frac { { \int { { \mu \left ( t \right ) g \left ( t \right ) \, d t } } + c } } { { \mu \left( t \right ) } } \end {equation} }$$
رابطه ۴

در رابطه فوق تابع $$\mu ( t )$$، عامل انتگرال‌ساز نامیده شده و با استفاده از رابطه زیر محاسبه می‌شود.

$$\large \begin {equation} \mu \left ( t \right ) = \, { { \bf{e } } ^ { \int { { p\left ( t \right ) \, d t } } } } \end {equation}$$

مراحل حل معادله دیفرانسیل خطی مرتبه اول

به منظور بدست آوردن پاسخ یک معادله دیفرانسیل خطی مرتبه اول، به ترتیب زیر عمل کنید:

1. معادله را به شکل استاندارد (در قالب رابطه ۱) بنویسید.
2. عامل انتگرال سازِ $$\mu ( t )$$ را بدست آورید.
3. کل معادله را در عامل انتگرال‌ساز ضرب کرده و نشان دهید که سمت چپ از قانون مشتقِ $$\left ( { \mu \left ( t \right ) y \left ( t \right ) } \right ) ^ { \prime }$$ پیروی می‌کند.
4. از طرفین عبارت بدست آمده، انتگرال بگیرید. در این مرحله در مورد ثابت‌ها دقت کنید.
5. پس از انتگرال‌گیری y را بدست آورید.

در ادامه مثال‌هایی ذکر شده که مطالعه آن‌ها را توصیه می‌کنیم.

مثال ۱

پاسخ معادله دیفرانسیل خطی زیر را بدست آورید.

$$\large \frac { { d v } } { { d t } } = 9 .8 - 0 . 1 9 6 v$$

در ابتدا، معادله را به شکل استاندارد و مطابق با رابطه زیر بیان می‌کنیم:

$$\large \frac { { d v } } { { d t } } + 0.196 v = 9.8$$

با توجه به رابطه فوق $$p(t)=0.196$$ بوده، در نتیجه عامل انتگرال‌ساز برابر است با:

$$\large \mu \left( t \right) = {{\bf{e}} ^ { \int { { 0.196dt} } } } = { { \bf{e} } ^ { 0 .196 t } }$$

با ضرب کردن طرفین معادله در عامل انتگرال‌ساز، می‌توان دید که سمت چپ عبارت بدست آمده برابر با مشتق تابع $$e ^ { 0.196t } v$$ است.

$$\large \begin {align*} { { \bf{e} } ^ { 0.196 t } } \frac { { d v } } { { d t } } + 0.196 { {\bf{e} } ^ { 0.196t } } v & = 9.8 { { \bf{e } } ^ { 0.196 t } } \\ { \left( { { { \bf{e } } ^ { 0.196t } } v } \right ) ^ \prime } & = 9.8 { {\bf{e} } ^ {0.196t } } \end {align*}$$

با انتگرال‌گیری از طرفین عبارت فوق، داریم:

$$\large \begin {align*} \int { { { { \left ( { { { \bf{e} } ^ { 0.196 t } } v } \right ) } ^ \prime } \, d t } } & = \int { { 9.8 { { \bf{e} } ^ { 0.196 t } } \, d t } } \\ { { \bf{e } } ^ {0.196t} } v + k & = 50 { { \bf{e}} ^ { 0.196 t } } + c \end{align*}$$

توجه داشته باشید که برآیند دو مقدار c و k را می‌توان برابر با ثابت c در نظر گرفت. بنابراین نهایتا تابع (v(t برابر با عبارت زیر بدست می‌آید.

$$\large v \left ( t \right ) = 5 0 + c { { \bf{e} } ^ { - 0.196 t } }$$

با توجه به رابطه فوق متوجه می‌شویم که چرا ضریب ثابت c دارای اهمیت است. در شکل زیر نمودار تابع به ازای چند c ترسیم شده است.

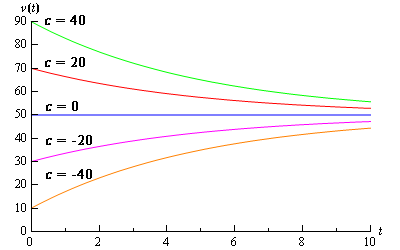
در حقیقت ثابت c با استفاده از شرایط اولیه یا شرایط مرزی بدست می‌آیند. در ادامه مثالی ذکر شده که در آن ضریب ثابت نیز بدست می‌آید.

مثال ۲

پاسخ معادله دیفرانسیل خطی زیر را بیابید.

$$\large \frac { { d v } } { { d t } } = 9.8 - 0.196 v \hspace {0.25in} , \ \ v \left ( 0 \right) = 48$$

فیلم آموزش محاسبات عددی با متمتیکا Mathematica – مقدماتی در فرادرس

کلیک کنید

مسئله دقیقا مشابه با مثال ۱ بوده و تنها تفاوت آن‌ها در ارائه شرایط اولیه است. بنابراین پاسخِ معادله برابر است با:

$$\large v \left ( t \right ) = 5 0 + c { { \bf{e} } ^ { - 0.196 t } }$$

بنابراین ضریب ثابت در t=0 به صورت زیر بدست می‌آید.

$$\large 48 = v \left( 0 \right ) = 50 + c \hspace {0.25in} \Rightarrow \hspace {0.25in} c = - 2$$

بنابراین پاسخ نهایی برابر است با:

$$\large v = 50 - 2{{\bf{e}}^{ - 0.196t}}$$

مثال ۳

پاسخ معادله دیفرانسیل خطی زیر را با توجه به شرط اولیه ارائه شده بیابید.

$$\large \cos \left ( x \right ) y ^ { \prime } + \sin \left( x \right)y = 2{\cos ^3} \left( x \right)\sin \left( x \right) - 1 \ \ \ : \hspace {0.25in} y \left ( {\frac { \pi } { 4 } } \right ) = 3 \sqrt 2 ,\hspace{0.25in}\,\,\,\,\,\,0 \le x < \frac {\pi } { 2 }$$

در ابتدا معادله به فرم استاندارد نوشته می‌شود.

$$\large \begin{align*}y' + \frac{{\sin \left( x \right)}}{{\cos \left( x \right)}}y & = 2{\cos ^2}\left( x \right)\sin \left( x \right) - \frac{1}{{\cos \left( x \right)}}\\ y' + \tan \left( x \right)y &= 2{\cos ^2}\left( x \right)\sin \left( x \right) - \sec \left( x \right)\end{align*}$$

در مرحله بعد، عامل انتگرال‌ساز به صورت زیر بدست می‌آید.

$$\large \mu \left( t \right) = {{\bf{e}}^{\int{{\tan \left( x \right)\,dx}}}} = {{\bf{e}}^{\ln \left| {\sec \left( x \right)} \right|}} = {{\bf{e}}^{\ln \,\,\sec \left( x \right)}} = \sec \left( x \right)$$

با ضرب عامل انتگرال‌ساز در طرفین معادله‌ی اصلی، به عبارت زیر می‌رسیم.

$$\large \begin{align*}\sec \left( x \right)y' + \sec \left( x \right)\tan \left( x \right)y & = 2\sec \left( x \right){\cos ^2}\left( x \right)\sin \left( x \right) - {\sec ^2}\left( x \right)\\ {\left( {\sec \left( x \right)y} \right)^\prime } & = 2\cos \left( x \right)\sin \left( x \right) - {\sec ^2}\left( x \right)\end{align*}$$

پس از انتگرال‌گیری از طرفین رابطه بالا، عبارت زیر بدست می‌آید.

$$\large \begin{align*}\int{{{{\left( {\sec \left( x \right)y\left( x \right)} \right)}^\prime }\,dx}} & = \int{{2\cos \left( x \right)\sin \left( x \right) - {{\sec }^2}\left( x \right)\,dx}}\\ \sec \left( x \right)y\left( x \right) & = \int{{\sin \left( {2x} \right) - {{\sec }^2}\left( x \right)\,dx}}\\ \sec \left( x \right)y\left( x \right) & = - \frac{1}{2}\cos \left( {2x} \right) - \tan \left( x \right) + c\end{align*}$$

توجه داشته باشید که در عبارت فوق، از رابطه مثلثاتی $$\sin \left( {2\theta } \right) = 2\sin \theta \cos \theta$$ استفاده شده است. با توجه به عبارت بالا، تابع y برابر می‌شود با:

$$\large \begin{align*}y\left( x \right) & = - \frac{1}{2}\cos \left( x \right)\cos \left( {2x} \right) - \cos \left( x \right)\tan \left( x \right) + c\cos \left( x \right)\\ & = - \frac{1}{2}\cos \left( x \right)\cos \left( {2x} \right) - \sin \left( x \right) + c\cos \left( x \right)\end{align*}$$

در مرحله بعد، با توجه به شرایط اولیه، ثابتِ c نیز به صورت زیر بدست می‌آید.

$$\large \begin{align*}3\sqrt 2 = y\left( {\frac{\pi }{4}} \right) & = - \frac{1}{2}\cos \left( {\frac{\pi }{4}} \right)\cos \left( {\frac{\pi }{2}} \right) - \sin \left( {\frac{\pi }{4}} \right) + c\cos \left( {\frac{\pi }{4}} \right)\\ 3\sqrt 2 & = - \frac{{\sqrt 2 }}{2} + c\frac{{\sqrt 2 }}{2}\\ c & = 7\end{align*}$$

با بدست آمدن c، پاسخ نهایی نیز برابر با تابع زیر بدست می‌آید.

$$\large y\left( x \right) = - \frac{1}{2}\cos \left( x \right)\cos \left( {2x} \right) - \sin \left( x \right) + 7\cos \left( x \right)$$

نمودار تابعِ بدست آمده، در ادامه ترسیم شده است.

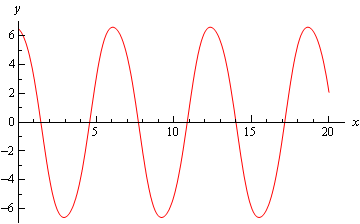
در این مطلب نحوه حل معادله دیفرانسیل خطی مرتبه اول توضیح داده شد. با این حال در آینده روش‌های حل معادلات دیفرانسیل مرتبه بالاتر را نیز توضیح خواهیم داد.

در صورت علاقه‌مندی به مباحث مرتبط در زمینه ریاضی، آموزش‌های زیر نیز به شما پیشنهاد می‌شوند:

• مجموعه آموزش‌های دروس ریاضیات
• مجموعه آموزش‌های ریاضیات و فیزیک پایه
• آموزش ریاضی پایه دانشگاهی
• معادله دیفرانسیل برنولی — از صفر تا صد
• معادلات دیفرانسیل — به زبان ساده

^^