تقسیم کسرها — به زبان ساده + حل تمرین و مثال

ما به‌راحتی می‌توانیم اعداد صحیح را بشماریم و ضرب و تقسیم آن‌ها انجام دهیم. اما در مواردی که با اعداد کسری کار می‌کنیم، کار کمی دشوارتر و زمان‌برتر خواهد بود. در چنین مواردی باید چه‌کار کنیم؟ اگر کسی نصف یک تکه از پیتزای شما را خورد، چقدر باقی می‌ماند؟ ما مطمئناً دیگر نه ۱ پیتزا داریم و نه ۰ پیتزا. اینجاست که باید با کسرها و عملیات روی آن‌ها آشنا باشیم. در این آموزش، با تقسیم کسرها آشنا می‌شویم.

کسر چیست؟

کسرها اعدادی هستند که با تقسیم تعریف می‌شوند و برای نشان دادن هر تعداد از قسمت‌های مساوی یک چیز به‌کار می‌روند. آن‌ها اعدادی حقیقی به‌فرم $$\frac p  q$$ هستند که در آن‌ها $$p$$ و $$q$$ اعدادی صحیح‌اند. عدد $$p$$ صورت کسر و عدد $$q$$  مخرج کسر نامیده می‌شود. بنابراین، در کسر $$\frac 23$$ عدد ۲ صورت و عدد ۳ مخرج کسر است و آن را «دو سوم» می‌خوانیم.

در اینجا یک نمایش بصری از مفهوم کسر ارائه می‌کنیم. به شکل زیر دقت کنید که به سه قسمت مساوی تقسیم و دو قسمت آن آبی شده است. می‌گوییم دو سوم این شکل آبی است و آن را با $$\frac {  2 } { 3 }$$ نشان می‌دهیم.

فرایندی که این $$\frac 23$$ حاصل شده را می‌توان در گام‌های زیر بیان کرد:

۱. ابتدا از کل شکل که ۱ واحد است شروع می‌کنیم.

۲. یک واحد را طبق مخرج (عدد ۳) به سه قسمت مساوی تقسیم می‌کنیم (یعنی $$\frac 13$$).

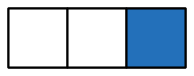
۳. نتیجه را در عدد صورت، یعنی ۲، ضرب می‌کنیم و به کسر $$\frac 23$$ می‌رسیم.

کسرها را می‌توان به سه دسته تقسیم کرد:

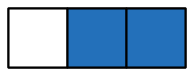
• کسرهای سره که در آن‌ها صورت از مخرج کوچک‌تر است، مثل $$\frac 45$$
• کسرهای ناسره که در آن‌ها صورت کسر از مخرج آن بزرگ‌تر است، مانند $$\frac 7 4$$.
• عدد آمیخته (مخلوط) که بخشی از آن یک عدد صحیح و بخشی از آن یک کسر است. بخش کسری این عدد همواره یک کسر سره است.

برای آنکه تقسیم کسرها را انجام دهیم، باید نحوه ضرب کسرها را بدانیم.

ضرب کسرها

ضرب کسرها کار آسانی است و برای انجام آن باید سه مرحله ساده زیر را طی کنیم:

1. ضرب صورت‌ها در یکدیگر
2. ضرب مخرج‌ها در یکدیگر
3. ساده‌سازی کسر با تقسیم صورت و مخرج بر بزرگ‌ترین مقسوم‌علیه‌های مشترک

برای آشنایی با نحوه محاسبه بزرگ‌ترین مقسوم‌علیه مشترک، به آموزش «ب م م یا بزرگترین مقسوم علیه مشترک چیست؟ — به زبان ساده (+ دانلود فیلم آموزش گام به گام)» مراجعه کنید.

مثال اول ضرب کسرها

فرض کنید می‌خواهیم ضرب کسری $$\frac { 2 } { 3 } \times \frac { 9 } { 4 }$$ را انجام دهیم.

حل: همان‌طور که گفتیم، صورت و مخرج را  در یکدیگر ضرب می‌کنیم و خواهیم داشت:

$$\large \dfrac { 2 } { 3 } \times \dfrac{ 9 } { 4 } = \dfrac { 2 \times 9 } { 3 \times 4 } = \dfrac { 18 } { 12 } .$$

از آنجا که بزرگ‌ترین مقسوم‌علیه مشترک بین دو عدد ۱۲ و ۱۸، عدد ۶ است، صورت و خرج را بر این دو عدد تقسیم می‌کنیم تا کسر ساده شود:

$$\large \dfrac { 2 } { 3 } \times \dfrac{ 9 } { 4 } = \dfrac { 2 \times 9 } { 3 \times 4 } = \dfrac { 18 } { 12 } .$$

بنابراین، داریم:

$$\large \frac { 2 } { 3 } \times \frac { 9 } { 4 } = \frac { 3 } { 2 }$$

اگر کسر یک کسر مخلوط باشد، ابتدا آن را به یک کسر ناسره تبدیل می‌کنیم، سپس ضرب را طبق مراحلی که پیش‌‌تر گفتیم انجام می‌دهیم. در ادامه، مثالی را از این مورد بررسی می‌کنیم.

مثال دوم ضرب کسرها

حاصل ضرب $$\frac { 2 } { 3 } \times 2 \frac { 3 } { 4 }$$ را به‌دست آورید.

حل: ابتدا دو کسر مخلوط را به کسرهای ناسره تبدیل می‌کنیم. بنابراین، داریم:

$$\large 1 \dfrac { 2 } { 3 } = \dfrac { 1 \times 3 + 2 } { 3 } = \dfrac { 5 } { 3 } , \quad 2 \dfrac { 3 } { 4 } = \dfrac { 2 \times 4 + 3 } { 4 } = \dfrac { 11 } { 4 }$$

سپس، صورت را در صورت و مخرج را در مخرج ضرب می‌کنیم:

$$\dfrac { 5 } { 3 }\times \dfrac { 11 } { 4 } = \dfrac { 5 \times 11}{ 3 \times 4} = \dfrac { 55 } { 12 }$$

از آنجا که بزرگ‌ترین مقسوم‌علیه مشترک دو عدد $$55$$ و $$12$$، عدد $$1$$ است، جواب نهایی $$\frac {55}{12}$$ خواهد بود.

دقت کنید که کاری مانند زیر انجام ندهید:

$$\large 1 \dfrac { 2 } { 3 } \times 2 \dfrac { 3 } { 4 } \neq ( 1 \times 2 ) \dfrac { 2 \times 3 } { 3 \times 4 } = 2 \dfrac { 1 } { 2 }$$

یک مثال دیگر را بررسی می‌کنیم.

مثال سوم ضرب کسرها

عبارت زیر را ساده کنید:

$$\large \dfrac { 4 } { 5 } \times 3 \dfrac { 3 } { 2 } .$$

حل: ابتدا کسر آمیخته را به یک کسر ناسره تبدیل می‌کنیم:

$$\large \frac { 3 } { 2 } = \frac { 3 \times 2 + 3 } { 2 } = \frac { 9 } { 2 } .$$

بنابراین، داریم:

$$\large \dfrac { 4 } { 5 } \times 3 \dfrac { 3 } { 2 } = \dfrac { 4 } { 5 } \times \dfrac { 9 } { 2 } =\dfrac { 4 \times 9 } { 5 \times 2 } = \dfrac { 3 6 } { 1 0 } = \dfrac { 1 8 } { 5 }$$

مثال چهارم ضرب کسرها

حاصل‌ضرب عبارت زیر را به‌دست آورید:‌

$$\large \frac { 2 } { 3 } \times 1 \frac { 3 } { 4 } \times \frac { 6 } { 5 } .$$

حل: ابتدا کسر آمیخته را به یک کسر ناسره تبدیل می‌کنیم:‌

$$\large 1 \frac 34 = \frac 75$$

بنابراین، خواهیم داشت:‌

$$\large \dfrac { 2 } { 3 } \times \dfrac { 7 } { 4 } \times \dfrac { 6 } { 5 } = \dfrac { 2 \times 7 \times 6 } { 3 \times 4 \times 5 } = \dfrac { 8 4 } { 6 0 } = \dfrac { 7 } { 5 }$$

تقسیم کسرها با کمک ضرب

تقسیم کسرها بسیار شبیه ضرب کسرها است. اگر فراگرفته‌اید که چگونه کسرها را در یگدیگر ضرب کنید، برای تقسیم کسرها، مشکلی نخواهید داشت.

با انجام مراحل زیر می‌توانیم کسرها را تقسیم کنیم:

1. هنگام تقسیم دو کسر، ابتدا مشخص کنید که کدام کسر مقسوم است (عددی که تقسیم می‌شود) و کدام کسر مقسوم‌علیه است (کسری که مقسوم بر آن تقسیم شده است).
2. جای صورت و مخرج کسر مقسوم‌علیه را با هم عوض کنید. به عبارت دیگر، کسر مقسوم‌علیه را معکوس یا وارون کنید.
3. اکنون صورت‌های مقسوم و مقسوم‌علیه جدید را در هم ضرب کنید.
4. مخروج‌های مقسوم و مقسوم‌علیه جدید را در هم ضرب کنید.

شکل زیر، مراحل این کار را برای دو کسر به‌خوبی نشان می‌دهد.

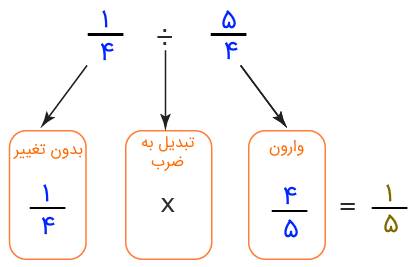
اگر بخواهیم به‌زبان ساده بگوییم، برا تقسیم دو کسر، باید جای صورت و مخرج آن را عوض کنید و آن را در کسر بالا ضرب کنید.

برای مثال، می‌خواهیم یک تقسیم را انجام دهیم. می‌خواهیم $$\frac 12$$ را بر $$\frac 13$$ تقسیم کنیم. این تقسیم را می‌توانیم به هرکدام از دو شکل زیر بنویسیم:

$$\large \frac 12 \div \frac 13$$  یا $$\large \frac {\frac 12}{\frac 13}$$

طبق آنچه گفتیم، ابتدا مقسوم و مقسوم‌علیه را مشخص می‌کنیم. در این تقسیم، مقسوم $$\frac 12$$ است و مقسوم‌علیه $$\frac 13$$.

در ادامه، مقسوم‌علیه را معکوس کرده و تقسیم را به ضرب تبدیل می‌کنیم. این یعنی اینکه خواهیم داشت:

$$\large \frac 12 \div \frac 13 = \frac 12 \color {green} {\times } \frac {\color {red} {3}}{\color {red} {1}} = \frac {1 \times 3 } { 2 \times 1 } = \frac 3 2$$

تقسیم کسرها روی محور

برای تقسیم کسرها روی محور، می‌توانیم چند حالت مختلف را بررسی کنیم که در ادامه به آن‌ها می‌پردازیم.

تقسیم عدد بر کسر

در این حالت، یک عدد طبیعی بر یک عدد کسری تقسیم می‌شود. برای مثال، فرض کنید می‌خواهیم $$2$$ را بر $$\frac 13$$ تقسیم کنیم. می‌خواهیم این تقسیم را روی محور نمایش دهیم.

برای انجام این تقسیم، ابتدا عدد $$2$$ را روی محور نشان می‌دهیم و برای انجام این کار دو واحد را روی محور جدا می‌کنیم. سپس برای نشان دادن $$\frac 13$$، هر واحد را به سه قسمت تقسیم می‌کنیم.

برای انجام تقسیم نیز، یک‌سوم یک‌سوم از صفر شروع می‌کنیم و می‌شماریم تا به عدد $$2$$ برسیم.

می‌بینیم که تعداد $$\frac 13$$ها شش تا است و بدین ترتیب حاصل تقسیم برابر با $$6$$ خواهد بود:

$$\large 2 \div \frac 13 = 6$$

تقسیم کسر بر عدد

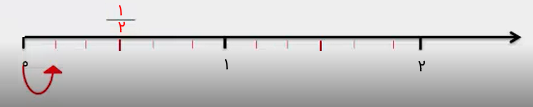
برای انجام تقسیم کسر بر عدد، ابتدا کسر را روی محور مشخص می‌کنیم، سپس آن را بر عدد تقسیم می‌کنیم. برای مثال، فرض کنید می‌خواهیم تقسیم $$\frac 12 \div 3$$ را انجام دهیم. اول از مقسوم شروع می‌کنیم و $$\frac 12$$ را روی محور مشخص می‌کنیم.

سپس آن $$\frac 12$$ را به سه قسمت تقسیم می‌کنیم و همین کار را برای بخش‌های باقیمانده محور انجام می‌دهیم.

اکنون باید ببینیم که آن یک‌سوم را که از یک‌دوم جدا کرده‌ایم، چه کسری از یک واحد است. با توجه به شکل زیر، می‌بینیم که قسمت مشخص‌شده $$\frac 16$$ واحد است. این یعنی اینکه حاصل تقسیم برابر با $$\frac 16$$ است.

تقسیم کسر بر کسر

در این حالت، یک کسر بر کسر دیگر تقسیم می‌شود. در محاسبه تقسیم دو کسر با استفاده از محور، حتماً باید دقت کنیم که مخرج آن‌ها با هم برابر باشد و اگر چنین نبود، با ضرب صورت و مخرج یکی از کسرها یا هردوی آن‌ها در یک عدد، مخرج‌ها را برابر کنیم.

برای مثال، فرض کنید می‌خواهیم تقسیم $$\frac 45 \div \frac 25$$ را انجام دهیم. می‌بینیم که مخرج‌ها برابر هستند. برای محاسبه حاصل این تقسیم، ابتدا عدد $$\frac 45$$ را روی محور مشخص می‌کنیم.

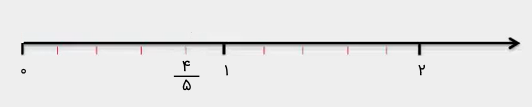
برای تقسیم کردن بر $$\frac 25$$، از صفر شروع می‌کنیم و دو پنجم دو پنجم جدا می‌کنیم تا به $$\frac 45$$ برسیم.

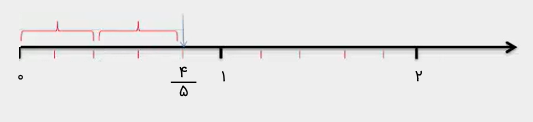
می‌بینیم که دو تا دو پنجم داریم و حاصل تقسیم برابر با $$2$$ خواهد بود.

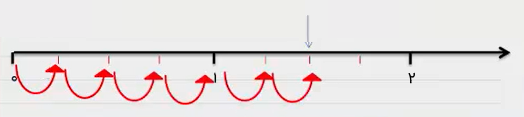
مثال دیگری را بررسی می‌کنیم. فرض کنید می‌خواهیم تقسیم $$\frac 322 \div \frac 14$$ را انجام دهیم. بدین منظور، ابتدا مخرج‌ها را یکی می‌کنیم (هردو مخرج را به $$4$$ تبدیل می‌کنیم):

$$\large \frac 32 \div \frac 14 = \frac 64 \div \frac 14$$

ابتدا $$\frac 64$$ را روی محور مشخص می‌کنیم. سپس یک‌چهارم یک‌چهارم می‌شماریم تا به $$\frac 64$$ برسیم. سپس تعداد $$\frac14$$هایی را که جدا کرده‌ایم می‌شماریم. می‌بینیم که تعداد آن‌ها $$6$$ عدد است. در نتیجه، حاصل تقسیم برابر با $$6$$ خواهد بود.

تقسیم کسرها به کمک شکل

این نوع تقسیم نیز چند حالت دارد که آن‌ها را به‌صورت جدا بررسی می‌کنیم.

تقسیم کسر کوچک‌تر از واحد بر عدد طبیعی

برای مثال، فرض کنید می‌خواهیم تقسیم $$\frac 12 \div 5$$ را انجام دهیم. ابتدا $$\frac 12$$ را با شکل مشخص می‌کنیم.

باید شکل را بر پنج قسمت تقسیم کنیم.

اکنون یکی از آن پنج قسمت را درنظر می‌گیریم. داحل این قسمتی که مشخص کرده‌ایم، چقدر رنگ شده است؟ یک خانه رنگ شده است. یکی از ۱۰ تا. پس حاصل تقسیم برابر با $$\frac {1}{10}$$ خواهد بود.

تقسیم یک عدد طبیعی بر کسر کوچک‌تر از واحد

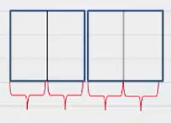
برای مثال، فرض کنید می‌خواهیم حاصل تقسیم $$2 \div \frac 12$$ را محاسبه کنیم. برای انجام این کار با کمک شکل، ابتدا عدد $$2$$ را مشخص می‌کنیم. برای این کار، دو واحد کامل رسم می‌کنیم.

اکنون می‌خواهیم آن را تقسین بر $$\frac 12$$ کنیم. یعنی هر شکل را باید به دو قسمت تقسیم کنیم.

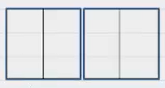
سپس، یک‌دوم‌ یک‌دوم تعداد شکل‌ها را بشماریم. می‌بینیم که چهار تا یک‌دوم داریم. پس جواب $$4$$ است.

تقسیم یک کسر کوچک‌تر از واحد بر کسر کوچک‌تر از واحد

برای مثال، می‌خواهیم حاصل تقسیم $$\frac 67 \div \frac 2 7$$ را به‌دست آوریم.

ابتدا $$\frac 67$$ را با شکل مشخص می‌کنیم.

سپس، قسمتی که رنگ شده را باید دو‌هفتم دوهفتم جدا کنیم.

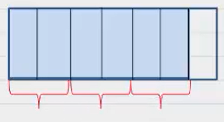
می‌بینیم که تعداد $$\frac 27$$ها سه‌تا شده‌اند. پس جواب تقسیم $$3$$ است.

تقسیم کسر بزرگ‌تر از واحد بر کسر کوچک‌تر از واحد

برای مثال، می‌خواهیم حاصل تقسیم $$2 \frac 23 \div \frac 23$$ را محاسبه کنیم.

ابتدا $$2 \frac 23$$ را با شکل نشان می‌دهیم.

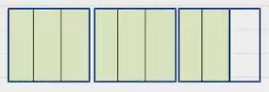
در ادامه، باید تقسیم $$\frac 23$$ را انجام دهیم. یعنی باید بخش‌های دو‌سوم دوسوم از شکل جدا کنیم.

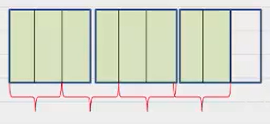
می‌بینیم که چهار تا دوسوم جدا کرده‌ایم. پس حاصل تقسیم برابر با $$4$$ خواهد بود.

مثال تقسیم کسرها

در این بخش، چند مثال را بررسی می‌کنیم.

مثال اول تقسیم کسرها

حاصل عبارت زیر را به‌‌دست آورید:

$$\large \frac { 2 0 } { 3 } - \frac { 1 } { 9 } \div \left [ \frac { 3 } { 7 } \times \left ( - \frac { 1 } { 4 } \right ) \times \left ( -\frac { 2 } { 3 } \right ) ^ 2 \right]$$

حل: ابتدا داخل پرانتزها، سپس کروشه‌ها را محاسبه می‌کنیم و خواهیم داشت:

$$\large \begin {aligned} \frac { 2 0 } {3 } -\frac { 1 } { 9 } \div \left [ \frac { 3 } { 7 } \times \left ( - \frac { 1 } { 4 } \right ) \times \left ( - \frac { 2 } { 3 } \right ) ^ 2 \right ] & = \frac { 2 0 } { 3 } - \frac { 1 } { 9 } \div \left [ \frac { 3 } { 7 } \times \left ( - \frac { 1 } { 4 } \right ) \times \left ( \frac { 4 } { 9 } \right ) \right ] \\ & = \frac { 2 0 } { 3 } - \frac { 1 } { 9 } \div \left [ \frac { 3 } { 7 } \times \left ( - \frac { 1 } { 9} \right ) \right ] \\ & = \frac { 2 0 } { 3 } + \frac { 1 } { 9 } \div \left [ \frac { 3 } { 6 3 } \right ] \\ & = \frac { 2 0 } { 3 } + \left ( \frac { 1 } { 9 } \times \frac { 6 3 } { 3 } \right ) \\ & = \frac { 2 0 } { 3 } + \left ( \frac { 7 } { 3 } \right ) \\ & = \frac { 2 7 } { 3 } \\ & = 9 . \ _ \square \end {aligned}$$

مثال دوم تقسیم کسرها

عبارت زیر را ساده کنید:

$$\large \frac { \hspace {2mm} \frac 2 3 \hspace {2mm} }{ \hspace {2mm} \frac 2 7 \hspace {2mm} } .$$

حل: هم صورت و هم مخرج کسر اصلی را در عدد $$21$$ ضرب می‌کنیم تا خرج کسرهای کوچک ساده شود. عدد $$21$$ کوچک‌ترین مضرب مشترک دو عدد $$3$$ و $$7$$ است. در نتیجه، خواهیم داشت:‌

$$\large \frac { \frac { 2 } { 3 } \times 21 } { \frac { 2 } { 7 } \times 2 1 } = \frac { 2 \times 7 } { 2 \times 3 } = \frac { 1 4 } { 6 } = \frac { 7 } { 3 } = 2 \frac { 1 } { 3 } .$$

مثال سوم تقسیم کسرها

چه تعداد $$\frac 17$$ در $$10 \frac 2 5$$ وجود دارد؟

حل: در واقع، سؤال از ما می‌خواهد حاصل تقسیم $$10 \frac 2 5$$ بر $$\frac 17$$ را محاسبه کنیم. ابتدا کسر آمیخته را به یک کسر ناسره تبدیل می‌کنیم و خواهیم داشت:‌

$$\large \begin {aligned} 1 0 \frac { 2 } { 5 } \div \frac { 1 } { 7 } & = \frac { 5 2 } { 5 } \div \frac { 1 } { 7 } \\ & = \frac { 5 2 } { 5 } \times 7 \\ & = \frac { 3 6 4 } { 5 } . \end {aligned}$$

مثال چهارم تقسیم کسرها

حاصل تقسیم عدد $$\frac 12$$ بر $$5$$ را به‌دست آورید.

حل: در این مثال مقسوم $$\frac 12$$ و مقسوم‌علیه $$\frac 51$$ است. باز هم به‌سادگی مراحل بالا را طی می‌کنیم. مقسوم‌علیه را معکوس و علامت تقسیم را به ضرب تبدیل می‌کنیم. بنابراین، خواهیم داشت:

$$\large \frac 12 \div5=\frac 12 \div \frac 51 = \frac 12 \color {green} {\times } \frac {\color {red} {1}}{\color {red} {5}} = \frac {1 \times 1 } { 2 \times 5 } = \frac {1}{10}$$

مثال پنجم تقسیم کسرها

حاصل تقسیم زیر را محاسبه کنید:

$$\large \frac { 6 } { \frac 13}$$

حل: ابتدا عدد $$6$$ را به‌‌صورت $$\frac 61$$ می‌نویسیم و تقسیم به‌صورت زیر درخواهد آمد:‌

$$\large \frac { \frac 61 } { \frac 13}$$

طبق روندی که گفتیم، کسر $$\frac 13$$ را معکوس کرده و تقسیم را به ضرب تبدیل می‌کنیم:

$$\large \frac { \frac 61 } { \frac 13} = \frac 61\div \frac 13 = \frac 61 \times \frac 31 = \frac {6 \times 3 } { 1 \times 1 } = \frac {18}{1} = 18$$

آزمون سنجش یادگیری تقسیم کسرها

در این بخش از مجله فرادرس، سطح اطلاعات شما در مبحث تقسیم کسرها را با طرح سوال‌های چندگزینه‌ای می‌سنجیم. پس از جواب دادن به تمام سوال‌ها، نتیجه آزمون برای شما به نمایش درمی‌آید.