تفاوت سیستم علی و غیرعلی چیست؟ – راهنمای جامع

در مباحث پردازش سیگنال شرط لازم برای این که یک سیستم «استاتیک» تلقی شود، مستقل بودن آن از مقادیر ورودی گذشته و آینده است. برای یک «سیستم علی» (Causal System) نیز شرایط تقریبا یکسان است و فقط اندکی تفاوت خواهد داشت. در این مطلب قصد داریم به بررسی تفاوت بین سیستم علی و «سیستم غیرعلی» (Non-Causal) بپردازیم و این مفهوم را با بیان چند مثال به صورت روشن‌تر بیان کنیم.

سیستم علی چیست؟

برای این که یک سیستم علی باشد فقط لازم است که از مقادیر ورودی آینده مستقل باشد. این امر بدین معنی است که وابستگی سیستم به مقادیر گذشته، مشکلی برای علی بودن سیستم به وجود نمی‌آورد. نکته مهمی که وجود دارد این است که یک سیستم علی را می‌توان به صورت فیزیکی پیاده‌سازی کرد. در ادامه به بیان چند مثال از سیستم‌های علی می‌پردازیم.

مثال ۱

سیستم زیر را در نظر بگیرید:

$$y ( t ) = x ( t )$$

در مورد سیگنال فوق، می‌توان گفت که سیستم فقط به مقادیر کنونی $$x$$ وابسته است. به عنوان مثال، اگر $$t = 3$$ را در معادله جایگذاری کنیم، نتیجه فقط برای آن لحظه از زمان نشان داده می‌شود. بنابراین، به دلیل این که هیچ وابستگی به مقادیر آینده در سیستم دیده نمی‌شود، می‌توان این سیستم را یک سیستم علی در نظر گرفت.

مثال ۲

یک سیستم با معادله $$y ( t ) = x ( t - 1 )$$ را در نظر بگیرید. تعیین کنید که آیا این سیستم علی است یا خیر؟

مشاهده می‌شود که این سیستم به مقادیر گذشته وابسته است. به عنوان مثال اگر $$t = 3$$ را در معادله جایگذاری کنیم، معادله به $$x ( 2 )$$ تغییر پیدا می‌کند که بر خلاف مقدار ورودی ما، یک مقدار مربوط به گذشته است. اما این سیستم در هیچ حالتی به مقادیر آینده وابستگی پیدا نمی‌کند. بنابراین این سیستم نیز یک سیستم علی محسوب می‌شود.

مثال ۳

سیستم با معادله $$y ( t ) = x ( t ) + x ( t + 1 )$$ را در نظر بگیرید. آیا این سیستم علی است؟

سیستم با معادله فوق، دارای دو بخش است. بخش اول $$x ( t )$$ است که در مثال اول به بررسی آن پرداختیم و دیدیم که فقط به مقادیر حال بستگی دارد. بنابراین این بخش علی است. حال بخش دوم سیستم، یعنی $$x ( t + 1 )$$ را در نظر می‌گیریم. واضح است که این بخش از سیستم به مقادیر آینده بستگی دارد: زیرا اگر $$t = 1$$ را در معادله جایگذاری کنیم، معادله به $$x ( 2 )$$ تغییر پیدا می‌کند که در این صورت سیستم به مقادیر آینده وابسته است. در نتیجه سیستم با معادله فوق، غیرعلی محسوب می‌شود. در تصویر زیر تفاوت بین یک سیستم علی و غیرعلی نشان داده شده است.

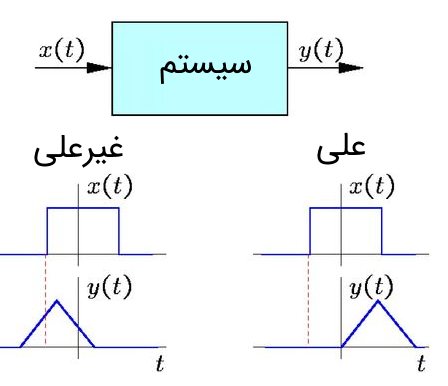
سیستم غیرعلی چیست؟

یک سیستم غیرعلی در تعریف کاملا برعکس سیستم علی در نظر گرفته می‌شود. در نتیجه اگر یک سیستم به مقادیر آینده ورودی‌ها در هر لحظه از زمان وابسته باشد، آن‌گاه گفته می‌شود که سیستم غیرعلی است. در مثال‌های زیر به بررسی چند نمونه از سیستم‌های غیرعلی می‌پردازیم.

فیلم آموزش پردازش سیگنال های واقعی در متلب در فرادرس

کلیک کنید

مثال ۱

یک سیستم با معادله $$y ( t ) = x ( t + 4 )$$ توصیف شده است. علی یا غیرعلی بودن این سیستم را بررسی کنید.

برای هر مقدار ورودی، این سیستم به مقادیر آینده آن وابستگی پیدا می‌کند. به عنوان مثال، اگر در معادله $$t = 2$$ را قرار دهیم، آن‌گاه سیستم به $$x ( 6 )$$ تغییر می‌کند که یک مقدار مربوط به آینده به شمار می آید. بنابراین به راحتی می‌توان گفت که سیستم غیرعلی است.

مثال ۲

سیستم با معادله $$y ( t ) = x ( t ) + x ( t + 2 )$$ را در نظر بگیرید. آیا سیستم علی است؟

در این حالت، $$x ( t )$$ یک تابع است که به صورت کامل فقط به مقادیر کنونی سیستم بستگی دارد. همچنین مثال قبل بسیار شبیه به قسمت دوم این سیستم، یعنی $$x ( t + 2 )$$ است. این تابع وابسته به مقادیر آینده است و مثلا به ازای $$t = 2$$ به $$x ( t = 4 )$$ وابسته است. به همین دلیل تابع کلی که برابر با مجموع دو تابع علی و غیر علی است، در نهایت غیرعلی در نظر گرفته می‌شود.

مثال ۳

آیا سیستم با معادله $$y ( t ) = x ( t - 1 ) + x ( t )$$ غیرعلی محسوب می‌شود؟

این سیستم به مقادیر حال و گذشته از ورودی داده شده وابسته است. هر مقداری را که در این تابع جایگذاری کنیم، هیچ وابستگی به مقادیر آینده به وجود نخواهد آمد. در نتیجه این سیستم علی است.

سیستم ضد علی (Anti-Causal System)

یک سیستم ضد علی تفاوت بسیار اندکی با یک سیستم غیرعلی دارد. یک سیستم ضد علی فقط به مقادیر ورودی‌های آینده وابسته است. به عبارت دیگر، یک سیستم ضد علی هیچ وابستگی به مقادیر حال و یا گذشته ورودی‌ها ندارد. مثال‌های زیر به روشن‌تر شدن مفهوم یک سیستم ضد علی کمک می‌کنند.

مثال ۱

سیستم با معادله $$y ( t ) = x ( t ) + x ( t + 1 )$$ را در نظر بگیرید. تعیین کنید آیا این سیستم ضد علی است یا خیر؟

همان طور که می‌دانیم این سیستم دو «زیرتابع» (Sub-function) دارد. یکی از این زیرتابع‌ها یعنی $$x ( t + 1 )$$، به مقادیر آینده ورودی‌ها بستگی دارد، اما بخش دیگر یعنی $$x ( t )$$، فقط به مقادیر ورودی‌های حال سیستم بستگی دارد. بنابراین تابع کلی به مقادیر حال به اضافه مقادیر آینده سیستم وابسته است و در نتیجه به عنوان یک سیستم غیر علی شناخته نمی‌شود.

مثال ۲

سیستم با معادله $$y ( t ) = x ( t + 3 )$$ را در نظر بگیرید. تعیین کنید که آیا این سیستم ضد علی است؟

اگر سیستم فوق را بررسی کنیم، متوجه می‌شویم که سیستم فقط به مقادیر آینده ورودی‌ها وابسته است. به عبارت دیگر، اگر مقدار $$t = 0$$ را در معادله جایگزین کنیم، سیستم به صورت $$x ( 3 )$$ نوشته خواهد شد که مقدار مربوط به آینده است. در نتیجه این سیستم یک مثال ایده‌آل از سیستم‌های ضد علی به حساب می‌آید.

اگر این مطلب برای شما مفید بوده است، آموزش‌های زیر نیز به شما پیشنهاد می‌شوند:

• تبدیل فوریه گسسته — از صفر تا صد
• انواع سیستم ها در پردازش سیگنال– به زبان ساده
• تبدیل فوریه سریع (fft) — به زبان ساده