تفاوت رگرسیون خطی و رگرسیون لجستیک چیست؟ – توضیح به زبان ساده

یادگیری نظارت شده روشی رایج در یادگیری ماشین است که خروجی یا رخدادهای آینده را پیشبینی میکند. در یادگیری نظارت شده از مجموعهدادههای برچسبگذاری شده برای یادگیری و تولید پیشبینیهای دقیق استفاده میشود. این روش از یادگیری ماشین خود به دو گروه «رگرسیون» (Regression) و «دستهبندی» (Classification) تقسیم میشود. «رگرسیون خطی» (Linear Regression) و «رگرسیون لجستیک» (Logistic Regression) دو نمونه از الگوریتمهای یادگیری ماشین نظارت شده هستند و به ترتیب در مجموعه روشهای رگرسیون و دستهبندی قرار میگیرند. در این مطلب از مجله فرادرس، پس از آشنایی با مفهوم این دو روش نظارت شده، به بررسی شباهتها و تفاوت رگرسیون خطی و رگرسیون لجستیک میپردازیم.
در این مطلب، ابتدا با انواع تحلیل رگرسیون آشنا میشویم و سپس به بررسی عمیقتر دو روش رگرسیون خطی و رگرسیون لجستیک میپردازیم. در ادامه شباهتها و همچنین تفاوت رگرسیون خطی و رگرسیون لجستیک را یاد میگیریم. در انتهای این مطلب از مجله فرادرس، موارد استفاده این دو الگوریتم را شرح داده و به چند نمونه از پرسشهای متداول در این حوزه پاسخ میدهیم.
در چه مواردی از تحلیل رگرسیون استفاده میشود؟
تحلیل رگرسیون بهطور خاص برای دو هدف متمایز از نظر مفهومی مورد استفاده قرار میگیرند:
- تحلیل رگرسیون کاربرد زیادی در مسائل پیشبینی داشته و از همین جهت یکی از بخشهای مهم یادگیری ماشین به شمار میرود.
- در برخی مسائل از تحلیل رگرسیون برای کشف روابط میان متغیرهای مستقل (Independent) و «وابسته» (Dependent) استفاده میشود.
در واقع، رگرسیون نوعی مدل یادگیری ماشین است که مقادیر عددی پیوسته یا مرتبط به چند دسته مختلف را پیشبینی میکند.
الگوریتم رگرسیون خطی چیست؟
«رگرسیون خطی» (Linear Regression) الگوریتمی نظارت شده در یادگیری ماشین است که فرض میکند رابطهای خطی میان متغیرهای وابسته و مستقل وجود دارد. به بیان سادهتر، این الگوریتم بهترین خط یا صفحه جداکننده دو یا تعداد بیشتری متغیر را پیدا میکند. مدل رگرسیون خطی، نتیجه را مطابق با متغیرهای مستقل پیشبینی کرده و رابطه میان آنها را کشف میکند. رگرسیون خطی را میتوان به دو زیر گروه دیگر تقسیم کرد:
- «رگرسیون خطی ساده» (Simple Linear Regression): رگرسیون خطی ساده به مدلی گفته میشود که رابطه میان یک متغیر مستقل و متغیری وابسته یا همان مقدار هدف را از طریق خطی صاف برآورد میکند.
- «رگرسیون خطی چندگانه» (Multiple Linear Regression): از رگرسیون خطی چندگانه برای ارزیابی رابطه میان دو یا چند متغیر مستقل با یک متغیر وابسته یا هدف استفاده میشود.
بهطور کلی، این الگوریتم از معادلهای خطی برای شناسایی خطی که بهترین «برازش» (Fit) و یا جدایی را ایجاد کند کمک میگیرد. از این طریق تصویرسازی و پیشبینی خروجی متغیرهای وابسته را ممکن میسازد.
مراحل رگرسیون خطی
همانطور که از اسمش پیداست، ایده الگوریتم رگرسیون خطی ساده، پیدا کردن معادله خطی است که بتواند ارتباط میان متغیرهای وابسته و مستقل را توصیف کند. در ادامه مراحل انجام این الگوریتم را بررسی میکنیم.

قدم ۱
بیایید فرض کنیم در مجموعهداده ما متغیر مستقل و تابعی از متغیر به شرح زیر است:
بدین ترتیب و با استفاده از رگرسیون خطی میتوانیم معادلهای مانند نمونه برای پیدا کردن بهترین برازش تعریف کنیم:
در عبارت فوق نماد متغیر هدف و به اُمین «متغیر پیشبینی کننده» (Predictor Variable) اشاره دارد. این معادله، همان معادله خط است که در آن نماد «شیب خط» (Slope) و «عرض از مبدا» (Intercept) است.
قدم ۲
حالا برای بهدست آوردن بهترین برازش، به متغیرهای و مقادیری تصادفی اختصاص داده و مقدار هدف یا همان را برای هر نمونه در مجموعهداده محاسبه میکنیم.
قدم ۳
پس از محاسبه مقدار پیشبینی شده خود از خروجی که آن را مینامیم، در این مرحله میخواهیم ببینیم پیشبینی ما چقدر دقیق است. در رگرسیون خطی مقدار این خطا، از طریق روش «میانگین مربعات خطا» (Mean Squared Error | MSE) بهدست میآید. در یادگیری ماشین به این روش «تابع زیان» (Loss Function) گفته میشود:
نماد $ n $ در معادله تابع زیان بیانگر تعداد کل نمونههای موجود در مجموعهداده است.
قدم ۴
برای کسب بهترین خروجی، باید مقدار تابع زیان را کمینه کنیم. برای کمینهسازی تابع زیان از روشی بهنام «گرادیان کاهشی» (Gradient Descent) استفاده میکنیم. در ادامه بیشتر با نحوه کارکرد گرادیان کاهشی آشنا میشویم.
گرادیان کاهشی
«تابع هزینه» (Cost Function) فرمولی ریاضیاتی برای محاسبه خطا یا همان تفاضل میان مقادیر پیشبینی شده و حقیقی است. اگر به معادله تابع زیان توجه کنیم، متوجه میشویم که میزان خطا به شکل عبارتی مرتبه دو محاسبه میشود. اگر تابع زیان را برای پارامترهای «وزنی» (Weights) یا همان m و c در معادله ترسیم کنیم، با یک منحنی «سهمی» (Parabolic) مواجه میشویم. حال و از آنجایی که هدف ما کمینهسازی تابع زیان است، باید به سمت کف این منحنی حرکت کنیم.
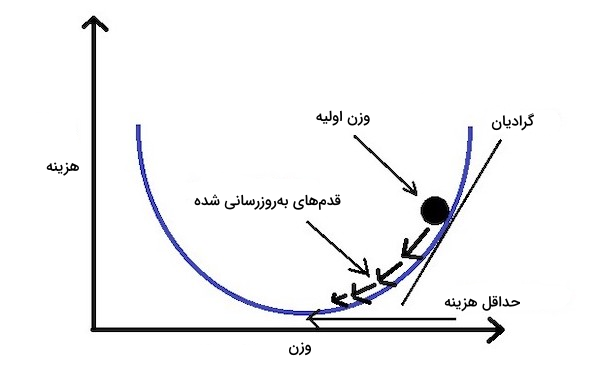
برای پیدا کردن جهت و مقدار حرکت زیان، باید از پارمترهای وزنی $ m $ و $ c $ نسبت به تابع زیان مشتق مرتبه اول بگیریم. سپس نتیجه را در ثابتی بهنام «نرخ یادگیری» (Learning Rate) یا \alpha ضرب کرده و مقدار وزنی جدید بهدست آمده را از وزن اولیه کم کنیم.
آنقدر این مرحله را تکرار میکنیم تا به مقدار کمینه یا به اصطلاح «کمینه سراسری» (Global Minima) برسیم. برای آنکه هدفی پایانی داشته باشیم، مقداری بسیار کم مانند ۰/۰۰۰۱ را به عنوان کمینه سراسری در نظر میگیریم. در صورتی که این حد آستانه را تعریف نکنیم، ممکن است هیچگاه به مقدار صفر مطلق نرسیم و تابع در حلقهای نامتناهی گرفتار شود.
قدم ۵
وقتی مقدار تابع زیان کمینه شد، در مرحله آخر میتوانیم مقدار خروجی $ y $ را بهازای هر نمونه $ x $، با استفاده از معادله خط و وزنهای بهینه شده بهدست آوریم.
الگوریتم رگرسیون لجستیک چیست؟
«رگرسیون لجستیک» (Logistic Regression) یک الگوریتم دستهبندی است که برای تقسیم عناصر یک مجموعه به دو گروه مجزا مورد استفاده قرار میگیرد. به مسائلی که دو گروه پاسخ دارند، مسائل «دستهبندی دودویی» (Binary Classification) گفته میشود. الگوریتم رگرسیون لجستیک با محاسبه احتمال هر نمونه داده، در واقع میزان تعلق آن به یکی از دو گروه مسئله را بهدست میآورد.
مراحل رگرسیون لجستیک
در رگرسیون لجستیک، مقداری احتمالی را به عنوان حد آستانه در نظر میگیریم. اگر احتمال نمونهای بیشتر از حد آستانه باشد، آن عنصر را در یک دسته و نمونههایی که مقداری کمتر از حد آستانه دارند را در دسته دیگر قرار میدهیم.
در ادامه، مراحل اجرای الگوریتم رگرسیون لجستیک را شرح داده و بررسی میکنیم.

قدم ۱
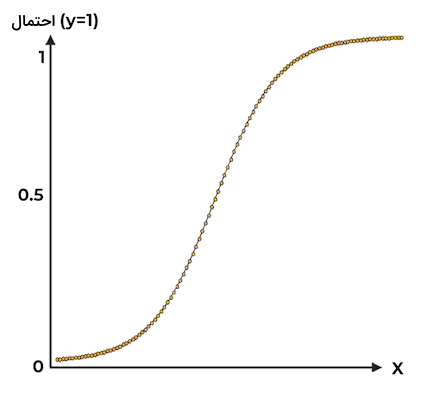
تابع رگرسیون خطی نمیتواند نمونههای پرت را بهدرستی دستهبندی کند. به همین خاطر در مسائل دستهبندی دو کلاسه عملکرد خوبی از خود نشان نمیدهد. در رگرسیون لجستیک برای پرهیز از این مشکل، خروجی مرحله قبل به تابع سیگموئید (Sigmoid) داده شده و به مقداری احتمالاتی تبدیل میشود. در واقع، تفاوت رگرسیون خطی و رگرسیون لجستیک در تابع فعالسازی سیگموئید خلاصه میشود. تابع سیگموئید مانند زیر تعریف میشود:
همانطور که در نمودار مشاهده میکنید، سیگموئید، تابعی است که هر عدد حقیقی را دریافت کرده و نتیجهای در بازه ۰ تا ۱ نتیجه میدهد.
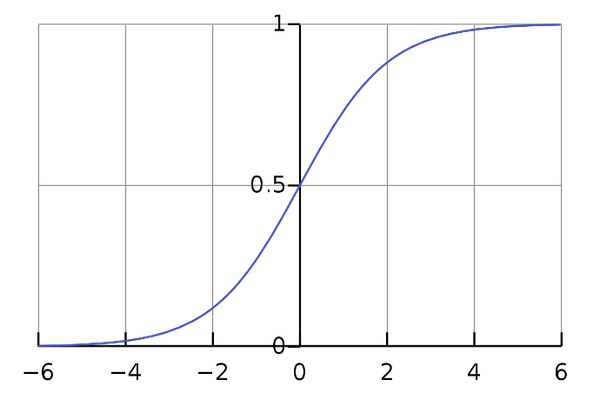
در نتیجه اگر خروجی حاصل از رگرسیون خطی را به عنوان ورودی به تابع سیگموئید بدهیم، خروجی به مقداری احتمالاتی بین ۰ تا ۱ تبدیل میشود.
قدم ۲
در نهایت مقدار خروجی تابع سیگموئید با استفاده از حد آستانهای از پیش تعریف شده، به یکی از مقادیر گسسته ۰ یا ۱ تبدیل میشود. حد آستانه بهطور معمول برابر با ۰/۵ گذاشته میشود تا فرایند دستهبندی دودویی به راحتی انجام شود.
حال که نحوه کارکرد و تفاوت رگرسیون خطی و رگرسیون لجستیک را یاد گرفتیم، در ادامه این مطلب از مجله فرادرس، با شرح یک مثال، درک عمیقتری از این دو الگوریتم بهدست میآوریم.
مقیاسه رگرسیون خطی و رگرسیون لجستیک
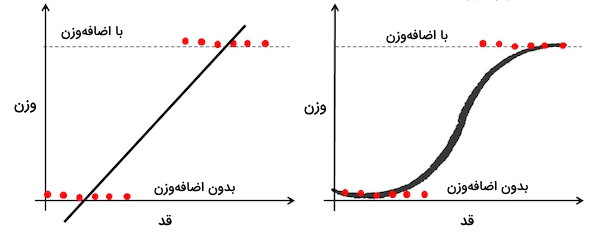
فرض کنید مسئلهای طرح شده و مجموعهدادهای شامل وزن و قد گروهی از افراد را در اختیار ما گذاشتهاند. وظیفه ما پیشبینی وزن افراد جدید نسبت به قدشان است.
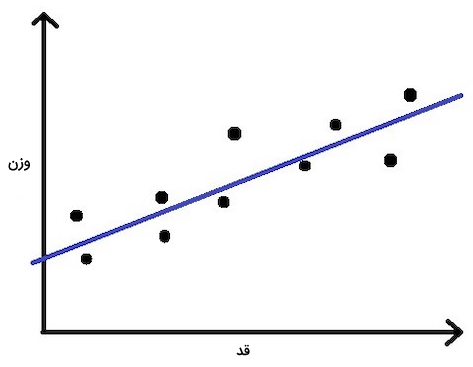
با بررسی و نگاهی دقیقتر، متوجه میشویم که رگرسیون خطی انتخاب خوبی برای این مسئله است. پس مدل رگرسیونی خود را با نمونههایی که شامل وزن و قد افراد میشود آموزش میدهیم. وقتی آموزش مدل تمام شد، میتوانیم تنها با داشتن مقدار قد، وزن یک نفر را پیشبینی کنیم.
حالا فرض کنید ویژگی دیگری بهنام اضافه وزن نیز داریم و باید با استفاده از وزن و قد، تشخیص دهیم که آیا فرد اضافه وزن دارد یا ندارد. یک مسئله دستهبندی که در آن باید مجموعهداده را به دو کلاسِ با اضافه وزن و بدون اضافه وزن تقسیم کنیم. در نتیجه برای این مسئله نیز مراحل رگرسیون خطی را دنبال کرده و مدل رگرسیونی مرتبط را میسازیم. این بار، تابع مطابق با دو پارامتر وزن و قد است و خط یا صفحه رگرسیونی، دو مجموعه گسسته مقادیر را از یکدیگر تفکیک میکند. از آنجایی که این تابع حساسیت بالایی نسبت به نمونههای پرت دارد، نتیجه چندان خوبی برای دستهبندی دو کلاس حاصل نمیشود. برای آنکه خروجی دستهبندی بهتری بهدست آوریم، نتیجه رگرسیون خطی را به تابع سیگموئید میدهیم. تابع سیگموئید برای هر خروجی، احتمال آن را برمیگرداند و با تعریف حد آستانه، بهراحتی خروجیها در دو گروهِ با اضافه وزن و بدون اضافه وزن قرار میگیرند.
متغیر و نوع خروجی
مدل رگرسیون خطی، بر متغیری وابسته و پیوسته متکی است. به این معنی که مقدار متغیر وابسته عددی است و در دسته یا گروه خاصی قرار نمیگیرد. در مقابل، مدلهای رگرسیون لجستیک بر اساس متغیرهای وابسته دودویی کار میکنند. به این صورت که متغیر وابسته تنها یکی از مقادیر ۰ یا ۱ را میپذیرد. همچنین خروجی رگرسیون خطی نیز مقداری پیوسته و در بازهای مشخص است. به عنوان مثال برای متغیرهای رگرسیون خطی میتوان به موارد زیر اشاره کرد:
- طول سقف: ۶۳ سانتیمتر، ۴۸ سانتیمتر، ۲ متر.
- ارتفاع: ۲ متر و ۲۰ سانتیمتر، ۲ متر و ۵ سانتیمتر، ۲ متر و ۲۵ سانتیمتر.
- «سرعت گریز» (Escape Velocity): ۴۲ هزار کیلومتر بر ساعت، ۳۵ هزار کیلومتر بر ساعت، ۵۰ هزار کیلومتر بر ساعت.
از طرفی دیگر، مدل رگرسیون لجستیک با مقادیر احتمالاتی به نمایش گذاشته میشود؛ از جمله:
- ۸۴/۳ درصد شانس شکست خوردن در مسابقه تنیس.
- ۲۳/۱ درصد شانس تصویب یک لایحه در مجلس.
- ۶۵/۱ درصد شانس قرنطینه شدن شهر در زمان فراگیری کرونا.
همچنین نتایج حاصل از رگرسیون خطی توزیعی «نرمال» (Normal) یا «گاوسی» (Gaussian) داشته و متغیرها در رگرسیون لجستیک با «توزیع دودویی» (Binomial Distribution) به نمایش گذاشته میشوند.
ارتباط میان متغیرها
برای تصمیمگیری در مورد انتخاب نوع مدل رگرسیون در مسائل مختلف، درک رابطه میان متغیرها امری ضروری است. رگرسیون خطی با رسم خطی بر روی محور، توصیفگر رابطه خطی میان متغیرها است. نتایج رگرسیون خطی به تحلیلگران اجازه میدهد تا با بررسی این روابط خطی، حرکت و پیشرفت متغیرها را در بازهای مشخص پیگیری کنند. در مقابل، رگرسیون لجستیک به مطالعه و تخمین احتمال رخدادهای مختلف شهرت دارد. در نتیجه نیازی به دنبال کردن روند حرکت رگرسیون لجستیک با استفاده از ساختارهای خطی نیست.

معادلات ریاضی
رابطه میان متغیرها برای مدلهای رگرسیون خطی را میتواند مانند نمونه تفسیر کرد:
تعریف هر یک از نمادها در معادله فوق به شرح زیر است:
- : نماد متغیر وابسته.
- : نماد اُمین متغیر پیشبینی کننده.
- : نماد میانگین تغییرات همزمان با افزایش .
در رگرسیون لجستیک نیز احتمال رخدادها یا مشاهده شدن هر نمونه، بهطور مشابه و از طریق رابطه زیر محاسبه میشود:
روش های توسعه داده شده
در رگرسیون خطی از روش «حداقل مربعات عادی» (Ordinary Least Squares) برای رسیدن به بهترین معادله برازش شده استفاده میشود. در این روش، ضرایب رگرسیون باید به نحوی انتخاب شوند که از مجموع فاصله میان متغیرها کاسته شود. در رگرسیون لجستیک اما از روش «تخمین بیشترین احتمال» (Maximum Likelihood Estimation | MLE) استفاده میشود که در آن ضرایب رگرسیون به قصد بیشینهسازی احتمال رخداد بهازای هر انتخاب میشوند.
نوع پیشبینی
مقدار خروجی یا همان در رگرسیون خطی، از طریق جمع مقادیر متغیرهای وروردی حاصل میشود.
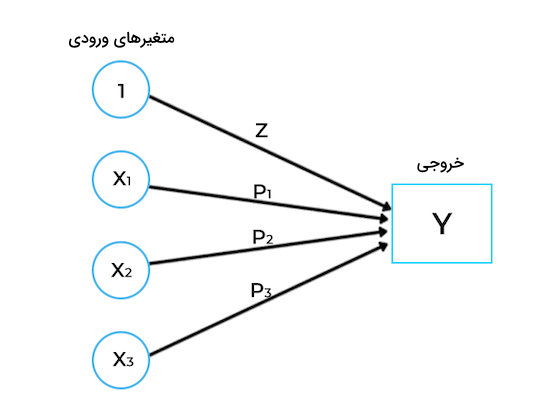
مدل رگرسیون خطی مقادیر ضرایب تا را مشخص کرده و دادههای آموزشی را بر همین ضرایب و برای پیشبینی خروجی () با خطای کمینه برازش میکند. تفاوت رگرسیون خطی و رگرسیون لجستیک در نوع پیشبینی به این صورت است که در رگرسیون لجستیک، ابتدا جمع مقادیر ورودی محاسبه شده و سپس تابع سیگموئید بر نتیجه اعمال میشود. خروجی این تابع غیر خطی، مقداری دودویی مانند ۰ و ۱ یا «درست» (True) و «نادرست» (False) است.
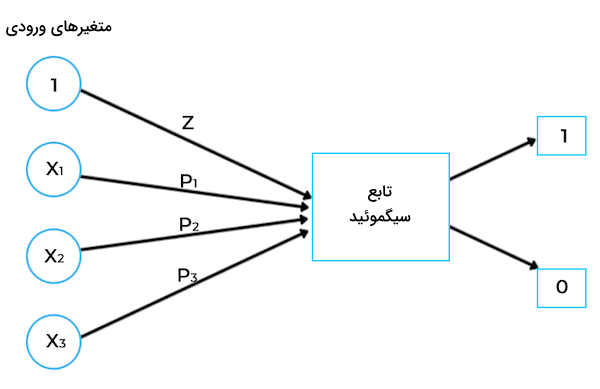
نحوه نمایش
تابع رگرسیون خطی را با تنها یک خط که آن را «خط رگرسیون» (Regression Line) نیز مینامند نشان میدهیم. این خط، مقدار پیشبینی شده را بهازای هر بهدست میآورد. فاصله میان نقاط داده و مقادیر پیشبینی شده در محور، نشاندهنده خطای مدل رگرسیون است.
در مقابل، منحنی رگرسیون لجستیک شکلی مانند حرف S انگلیسی دارد. در این نوع از رگرسیون، تغییر در ضرایب بر جهت و شیب منحنی اثر میگذارد. در نتیجه اگر شیب مثبت باشد، منحنی S مانند است و در صورتی که شیب منفی باشد، منحنی شمایلی شبیه به حرف Z دارد.
همبستگی میان متغیرهای مستقل
یک مدل رگرسیون خطی ساده، همبستگی میان متغیرهای وابسته و مستقل را تعریف میکند. همچنین در رگرسیون خطی چندگانه میتوان یک یا چند مورد از همبستگی میان متغیرهای مختلف را مشخص کرد. از سوی دیگر در رگرسیون لجستیک، متغیرهای مستقل هیچ همبستگی با یکدیگر ندارند.
وزن و مشاهدات
تفاوت رگرسیون خطی و رگرسیون لجستیک در این است که رگرسیون خطی، از معیار «جذر میانگین مربعات خطا» (Root Mean Square Error | RMSE) و رگرسیون لجستیک از معیار «دقت» (Precision) برای پیشبینی مقادیر وزنی نقاط داده استفاده میکند. روش RMSE دقت مدل خطی را محاسبه کرده و به خوبی خطای پیشبینی شده توسط مدل لجستیک را مشخص میکند.
توابع فعالسازی
مدلهای رگرسیونی در یادگیری ماشین از «توابع فعالسازی» (Activation Functions) متفاوتی استفاده میکنند تا از این طریق، نورونهای فعال و غیر فعال شبکه عصبی را مشخص کنند. در رگرسیون خطی نیازی به تابع فعالسازی نیست؛ اما هنگام تبدیل یک مدل خطی به مدل لجستیک، بهرهگیری از تابع فعالسازی ضرورت پیدا میکند. در رگرسیون لجستیک، برای تبدیل خروجی به مقداری دستهای از تابع سیگموئید به عنوان تابع فعالسازی استفاده میشود.

تفسیرپذیری
مدلهای احتمالاتی خطی و لجستیک را میتوان به ترتیب و از طریق معادلات زیر تعریف کرد:
معادله اول همان مدل خطی و معادله دوم مربوط به مدل لجستیک است. همچنین حرف نماد احتمال است. با نگاه به این دو معادله، ممکن است مدل خطی راحتتر از مدل لجستیک بهنظر برسد. به عنوان مثال فرض کنید مقدار در معادله اول برابر با ۰/۰۷ است؛ به این معنی که افزایش در مقدار باعث افزایش ۷ درصدی احتمال نهایی میشود. حالا در معادله دوم یا همان مدل لجستیک، اگر مقدار متغیر را برابر با ۰/۰۷ در نظر بگیریم، یعنی احتمال لگاریتمی برای نمونه به میزان ۰/۰۷ افزایش پیدا کرده است. از همین جهت ممکن است مدل خطی تفسیرپذیرتر بهنظر برسد.
قاعده کلی
در شرایطی که قرار است دادهها به دو گروه مختلف تقسیم شوند، استفاده از الگوریتم رگرسیون لجستیک پیشنهاد میشود. با این حال اگر خروجی احتمال حاصل از رگرسیون لجستیک چندان به ۰ یا ۱ نزدیک نباشد و مقادیری مانند ۰/۳۰ و ۰/۷۰ را شامل شود، رگرسیون خطی نیز گزینه مناسبی برای انتخاب خواهد بود. گرچه در این مورد تفاوت رگرسیون خطی و رگرسیون لجستیک زیاد نیست و هر دو روش عملکرد خوبی دارند، تفسیر رگرسیون خطی راحتتر از رگرسیون لجستیک است. مثالی را تصور کنید که در آن میخواهید احتمال یک نظرسنجی را مدلسازی کنید. تمامی احتمالات مدلسازی شده مقادیری بین ۰/۲۵ و ۰/۷۵ خواهند داشت. بهخاطر قابلیت تفسیرپذیری بیشتر، استفاده از رگرسیون خطی در چنین مثالی مناسبتر است. در مقابل اگر بخواهیم احتمال جعلی بودن تراکنشهای یک دستگاه خودپرداز یا ATM را شبیهسازی کنیم، احتمالات مدلسازی شده مقادیری بین ۰/۰۰۰۰۰۳ و ۰/۲۵ خواهند داشت و در چنین موقعیتی، مدل لجستیک نسبت به خطی عملکرد بهتری دارد.

سرعت محاسباتی
مدلهای خطی و لجستیک سرعت محاسباتی متفاوتی دارند. از آنجایی که رگرسیون لجستیک برای برازش مدل، تخمین بیشترین احتمال یا به اصطلاح MLE را بهطور دورهای و تکرارشونده محاسبه میکند، از ابتدا سرعت کمتری دارد. البته این کاهش سرعت در شرایطی که مجموعهداده کوچک باشد یا بخواهیم مدل سادهای را برازش کنیم، تفاوت چندانی ایجاد نمیکند. در مقابل رگرسیون خطی با اجرای روش حداقل مربعات عادی، نسبت به مدل لجستیک سریعتر است.
کاربردها
دو مدل رگرسیون خطی و لجستیک در مجموعه کاربردهای متنوعی مورد استفاده قرار میگیرند. بهطور مشخص از رگرسیون خطی در علوم داده، کسبوکار، امور مالی و بازاریابی بهرهبرداری میشود:
- تجارت: شرکتها برای درک بهتر و موثرتر فعالیتهای خود مطابق با روند بازار از رگرسیون خطی استفاده میکنند. از طریق رگرسیون خطی پارامترهای مختلفی از جمله ارزیابی جریانات فراگیر (Trend)، تشخیص گرایشات و رفتار مشتری، پیشبینی میزان فروش در آیند و تخمین حاشیه سود و ضرر قابل بررسی هستند. بهطور کلی، مدلهای خطی عملکرد کلی کسبوکارها را بهبود میبخشند.
- تحلیل بازار: کسبوکارها با کمک مدلهای رگرسیون خطی تجزیه و تحلیلهای جامعی از شرایط بازار تهیه میکنند. شرکتها با بررسی معیارهایی همچون قیمتگذاری، کمپینهای بازاریابی و تبلیغات، استراتژیهای بازاریابی بسیاری را مورد سنجش قرار میدهند.
- ارزیابی زیان مالی: رگرسیون خطی یکی از الگوریتمهای رایج برای تحلیلگران صنایع مالی است. از این الگوریتم برای پیشبینی بازدهی، «مدیریت مجموعه پروژهها» (Portfolio Management) و ارزشگذاری سرمایه استفاده میشود. این مدلها نقش حیاتی در کشف رابطه میان سرمایه بازگشتی و خطر بازار مربوطه دارند.

بهطور مشابه، از جمله کاربردهای رگرسیون لجستیک میتوان به موارد زیر اشاره کرد:
- پزشکی: به عنوان مثال، متخصصان علم پزشکی از رگرسیون لجستیک برای مطالعه تاثیر دویدن بر احتمال مصدومیت زانو استفاده میکنند. در این مثال، خروجی به دو دسته آسیب شدید و آسیب خفیف زانو تقسیم میشود. خروجی مدل مشخص میکند که دویدن شدید تا چه اندازه بر احتمال مصدوم شدن ورزشکار تاثیر میگذارد.
- «رتبهبندی اعتبار» (Credit Scoring): رتبهبندی اعتبار خودکار، یکی دیگر از مزایای توسعه مدلهای پیشبینی کننده از طریق الگوریتم رگرسیون لجستیک است. هنگام محاسبه رتبههای اعتبار، پارامترهای مختلفی از جمله وضعیت حساب، تاریخچه اعتبار، وضعیت تاهل و جنسیت در نظر گرفته میشوند. با افزایش تعداد متغیرهای مورد نیاز، بهطور معمول مدلهای لجستیک نتایج قابل قبول و دقیقی ارائه میدهند.
- پایش رفتار مشتری: رگرسیون لجستیک نوعی مدل یادگیری ماشین است که رفتار مشتری را در پلتفرمهای آنلاین، شبکههای اجتماعی و حتی بازیهای ویدئویی دنبال میکند. این مدلها سریع و خودآموز بوده و فهم آنها نیز آسان است؛ مواردی که رگرسیون لجستیک را به انتخابی ایدهآل برای خودکارسازی و ارتقاء تجربه کاربری تبدیل میکند.
- رزرو هتل: وبسایتهای زیادی در زمینه رزرو هتل از رگرسیون لجستیک برای پیشبینی رفتار، علایق و خواستههای مسافر بهره میبرند. از دادههای بهدست آمده برای پیشنهاد سفرهای تفریحی آینده و محل اقامت به مسافران استفاده میشود. مدلهای بهکار گرفته شده در این حوزه، به دادههای حاصل از تعامل دراز مدت کاربر با سیستم متکی هستند. کسب این اطلاعات از طریق مدلهای رگرسیون لجستیک، احتمال آنکه کاربر برای سفر بعدی از سرویس شما خرید کند را بالا میبرد.
- ویرایش متن: ابزارهای ویرایش متن بسیاری از مدلهای رگرسیون لجستیک برای تصحیح انواع خطاها مانند خطاهای دستوری، نحوی، املایی و حتی ساختاری جمله استفاده میکنند. این امکان وجود دارد که با آموزش دادن این مدلها، واژگان توهینآمیز و حساس را مطابق با انتخاب کاربر و قابلیتهای نرمافزاری در دسترس، نشانهگذاری و حذف کرد.
گرچه تفاوت رگرسیون خطی و رگرسیون لجستیک در زمینههای مختلف به چشم میآید، با این حال هر کدام بهخاطر قابلیتهایی همچون تفسیرپذیری، کارآمدی و پیادهسازی راحت، گستره کابردی وسیعی دارند.
شباهت های رگرسیون خطی و رگرسیون لجستیک
رگرسیون خطی و همچنین رگرسیون لجستیک، هر دو در دسته الگوریتمهای یادگیری ماشین نظارت شده قرار میگیرند. رگرسیون خطی و رگرسیون لجستیک انواع مدلهای «رگرسیون پارامتری» (Parametric Regression) هستند که برای پیشبینی از معادلات خطی استفاده میکنند. شباهتهای این دو مدل در همینجا تمام میشود و از نظر عملکردی دو الگوریتم متفاوت هستند.

تفاوت رگرسیون خطی و رگرسیون لجستیک
رگرسیون خطی و رگرسیون لجستیک دو نمونه از محبوبترین روشهای آماری برای مدلسازی و تجزیه و تحلیل داده هستند. شاید این دو الگوریتم در ظاهر شبیه بهنظر برسند اما علاوهبر کاربرد، نحوه عملکرد متفاوتی نیز دارند. از جمله این تفاوتها میتوان به موارد زیر اشاره کرد:
- در حالی که رگرسیون خطی حل مسائل رگرسیونی را بر عهده دارد، از رگرسیون لجستیک در مسائل دستهبندی استفاده میشود.
- خروجی در رگرسیون خطی مقداری پیوسته و در رگرسیون لجستیک گسسته است.
- در حالی که هدف از رگرسیون خطی پیدا کردن بهترین خط برازش شده است، رگرسیون لجستیک یک قدم جلوتر بوده و مقادیر خط را بر منحنی سیگموئید برازش میکند.
- روش محاسبه تابع زیان در رگرسیون خطی، همان میانگین مربعات خطا است و در رگرسیون خطی از روش تخمین بیشترین احتمال یا MLE استفاده میشود.
- در رگرسیون خطی، تفسیر ضرایب متغیرهای مستقل به مراتب راحتتر از رگرسیون لجستیک است. در رگرسیون لجستیک بسته به نوع متغیرها و ویژگیها، تفسیر ضرایب متفاوت خواهد بود.
- پیشبینی متغیر وابسته در رگرسیون خطی، با بهرهگیری از مجموعه متغیرهای مستقل انجام میشود. اما در رگرسیون لجستیک، متغیر وابسته پیشبینی شده «دستهای» (Categorical) است. خروجی رگرسیون لجستیک باید مقداری پیوسته مانند قیمت یا سن باشد. در حالی که خروجی رگرسیون لجستیک مقداری دستهای مانند ۰ یا ۱ و بله یا خیر است.
با وجود برخی شباهتهای سطحی، تفاوت رگرسیون خطی و رگرسیون لجستیک به فرضیات و مسائل متفاوتی که حل میکنند برمیگردد. رگرسیون لجستیک مقادیر دستهای را پیشبینی میکند و نتیجه رگرسیون خطی، مقداری عددی و پیوسته است.
موارد استفاده رگرسیون خطی و رگرسیون لجستیک
الگوریتم رگرسیون خطی تنها در مسائلی کاربرد دارد که میخواهیم خروجی کمی باشد. برخی برای دستهبندی دودویی نیز از رگرسیون خطی استفاده میکنند؛ اما رگرسیون لجستیک در مسائل دستهبندی عمومیت بیشتری داشته و تجزیه و تحلیل خروجی آن نیز راحتتر است.

سوالات متداول
پس از آشنایی با تفاوت رگرسیون خطی و رگرسیون لجستیک و یاد گرفتن نحوه کارکرد هر کدام از این روشها، حال زمان خوبی است تا در این بخش، به برخی از پرسشهای متداول درباره رگرسیون خطی و رگرسیون لجستیک پاسخ دهیم.
رگرسیون لجستیک چگونه با رگرسیون خطی مرتبط است؟
هم رگرسیون خطی و هم رگرسیون لجستیک از مجموعهداده برچسبدار استفاده میکنند و هر دو روش از الگوریتمهای یادگیری ماشین نظارت شده هستند.
تفاوت رگرسیون خطی و رگرسیون لجستیک در چیست؟
از رگرسیون خطی برای حل مسائل رگرسیون استفاده میشود و رگرسیون لجستیک در مسائل دستهبندی کاربرد دارد.
آیا رگرسیون لجستیک همان رگرسیون خطی است؟
رگرسیون لجستیک را نوعی مدل خطی در نظر میگیرند؛ چرا که خروجی آن به مجموع ورودیها و پارامترها وابسته است.
جمعبندی
تحلیل رگرسیون از طریق آشکارسازی رابطه میان مجموعه متغیرهای وابسته و مستقل، الگوهای موجود در داده را شناسایی میکند. ابزاری لازم در یادگیری ماشین و تحلیل آماری که خروجی سیستمها و دادهها را پیشبینی کرده و وابستگی میان متغیرها را آشکار میسازد. در این مطلب از مجله فرادرس، به بررسی تفاوت رگرسیون خطی و رگرسیون لجستیک پرداختیم و پس از آشنایی با نحوه کارکرد هر یک از این الگوریتمها، به چند مورد از کاربردهای آنها نیز اشاره کردیم. رگرسیون خطی و لجستیک، دو نوع خاص از تحلیل رگرسیون هستند که به ترتیب در مسائل رگرسیون و دستهبندی مورد استفاده قرار میگیرند.












