تداخل امواج — به زبان ساده

پیشتر در وبلاگ فرادرس در مورد امواج الکترومغناطیسی و حتی نحوه تولید آنها بحث شد. اما در مواردی در طبیعت ممکن است دو یا چند موج به هم برخورد کرده و منجر به ایجاد موجی جدید شود. از این رو در این مطلب قصد داریم تا در مورد نوع جدیدی از تاثیرگذاری امواج تحت عنوان تداخل امواج صحبت کنیم.
تداخل امواج
ناحیهای از فضا را تصور کنید که در آن دو یا چند موج در آن در حال حرکت هستند. بر اساس اصل برهمنهی، جابجایی خالص بهصورت جمع اسکالر یا برداری دو موج بدست میآید. تداخل امواج نوعی برهمنهی محسوب میشود که در آن دو موج به هم برخورد کرده و ممکن است یکدیگر را تخریب یا تقویت کنند. در شکل زیر شماتیک چنین برخوردی نشان داده شده است.
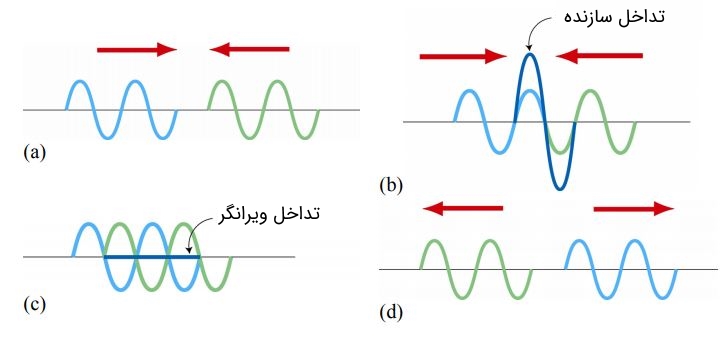
دو موج با معادلات زیر را در نظر بگیرید.
با جمع زدن جبری دو معادله فوق، به معادله زیر خواهیم رسید.
اگر دامنه موج فوق از دامنههای هریک از امواج اولیه بزرگتر باشد در این صورت تداخل، تحت عنوان تداخل سازنده شناخته میشود. در غیر اینصورت تداخل را ویرانگر مینامند. بهعنوان یک مثال، ترکیب دو موج زیر را در لحظه در نظر بگیرید.
با ترکیب این دو موج، موج زیر بدست میآید.
توجه داشته باشید که برای سادهسازی جمع بالا، از قاعده زیر استفاده شده است.
با توجه به ، میتوان حاصل جمع دو ترم سینوس و کسینوس را مطابق با عبارت زیر ساده کرد.
اختلاف فاز نیز برابر است با:
با این فرضیات جمع دو موج فوق بهصورت زیر قابل بیان میشود:
اختلاف فاز موج بدست آمده نیز برابر است با:
در شکل زیر دو موج اولیه و موج بدست آمده از آنها، ترسیم شدهاند.
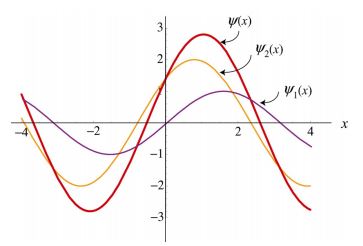
همانطور که مشاهده میکنید بیشترین مقدار دامنه در مکان رخ میدهد. از طرفی بیشترین مقدار دامنه، افزایش یافته بنابراین میتوان گفت تداخل امواج در این مکان از نوع سازنده محسوب میشود.
نور
همانطور که در مطلب فوتون نیز بیان شد، نور نوعی موج الکترومغناطیسی محسوب میشود. حال فرض کنید میخواهیم الگوی تداخل دو یا چند موج نوری را بدست آوریم. بدین منظور به یاد داشته باشید که دو موج نوری که به یکدیگر برخورد میکنند باید دو شرط زیر را داشته باشند.
- منابع نور باید همدوس باشند. این جمله به معنای آن است که امواج تخت ناشی شده از منابع باید در فاز ثابتی نسبت به یکدیگر قرار داشته باشند. برای نمونه اگر دو موج در اختلاف فاز نسبت به یکدیگر قرار داشته باشند در این صورت، اختلاف آنها نباید با زمان تغییر کند.
- نور باید مونوکروماتیک باشد. این ویژگی به معنای آن است که موج نوری مذکور تنها از یک طول موج تشکیل شده باشد.
توجه داشته باشید که نور منتشر شده از یک لامپ رشتهای، غیرهمدوس است چراکه این نور شامل طولموجهای مختلفی بوده، همچنین اختلاف فاز آنها نسبت به هم مقدار ثابتی نمیماند. از این رو الگوی تداخلی را نمیتوان برای آن تعریف کرد.
آزمایش دوشکاف یانگ
در سال ۱۸۰۱ توماس یانگ آزمایشی انجام داد که با استفاده از آن توانست ماهیت موجی نور را بررسی کند. شماتیک آزمایش دوشکاف در ادامه نشان داده شده است.
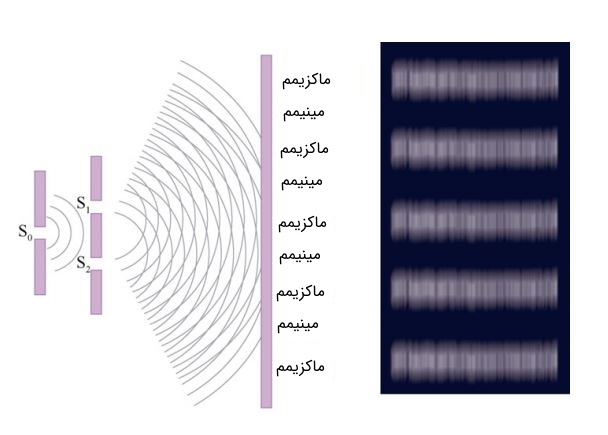
در این آزمایش یک منبع نوری تکموج به یک صفحهای با شکاف برخورد میکند. در پشت این شکاف، صفحه دومی با دو شکاف و قرار دارد. در حقیقت هریک از این دو شکاف، دو منبع نوری جداگانه محسوب میشوند. همانطور که در شکل فوق نیز نشان داده شده، بخشهای روشن نشاندهنده تداخل سازنده دو موج و بخشهای تیره نشاندهنده تداخل ویرانگر دو موج هستند. در شکل زیر نیز شماتیک تداخل دو موج نشان داده شده است.
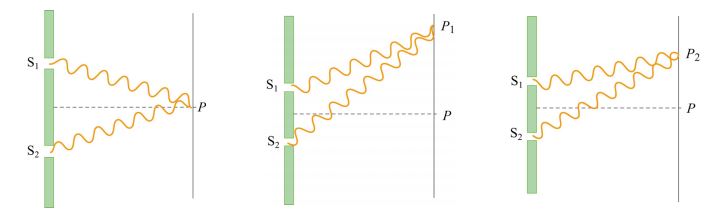
بهمنظور تحلیل کمی نحوه تداخل امواج، طولها و زوایا را مطابق با شکل زیر نامگذاری میکنیم.
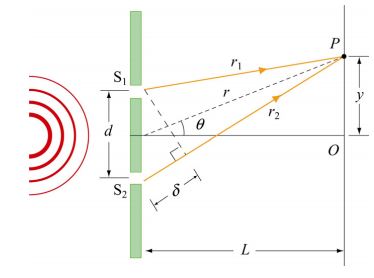
نوری را در نظر بگیرید که در نقطهای همچون روی پرده پشت دوشکاف افتاده است. فرض کنید دو شکاف در فاصلهای برابر با از هم قرار گرفتهاند. در این صورت نور عبور کرده از شکاف دوم مسافتی بیشتر به اندازه نسبت به نور عبور کرده از شکاف اول، طی کرده است. به این فاصله اضافه، اختلاف مسیر گفته میشود و مقدار آن را میتوان با استفاده از قانون کسینوسها، مطابق با رابطه زیر بدست آورد.
به همین صورت مقدار نیز برابر میشود با:
با ادغام دو رابطه فوق داریم:
در حالتی حدی که است، فاصله تا پرده بسیار بیشتر از فاصله دو شکاف است. در این حالت جمع و را میتوان بهصورت تقریبی برابر با در نظر گرفت؛ همچنین اختلاف اندازه مسیر دو موج در این حالت برابر است با:
در این حالت، همانطور که در شکل زیر نشان داده شده، مسیر دو پرتو تقریبا بهصورت موازی در نظر گرفته میشود.
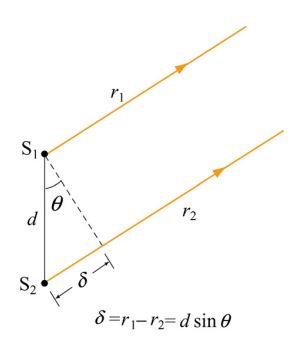
هم فاز بودن یا غیر هم فاز بودن دو موج با توجه به اختلاف فاصله دو پرتو () تعیین میشود. تداخل سازنده زمانی رخ میدهد که صفر یا ضرایبی طبیعی از مقدار طول موج باشد. در حقیقت تداخل سازنده زمانی رخ میدهد که اختلاف فاصله برابر با مقدار زیر باشد.
(تداخل سازنده)
تحت عنوان عدد مرتبه شناخته میشود. مرتبه صفرم، ماکزیمم میزان نور بوده و به بخش نورانی قرار گرفته در مرکز در اشاره میکند. همچنین مرتبه اول () به هریک از بخشهای نورانی قرار گرفته در اطراف مرکز اشاره میکند.
از طرفی دیگر زمانی که مضربی فرد از مقدار باشد، امواج به اندازه ۱۸۰ درجه در نقطه نسبت به هم اختلاف فاز خواهند داشت. این حالت ایجاد کننده تداخلی ویرانگر خواهد بود که نشاندهنده بخش تاریک الگو است. اختلاف فاصله مربوط به تداخل ویرانگر بهصورت زیر است.
(تداخل ویرانگر)
در شکل زیر هر دو حالت ایجادکننده امواج ویرانگر و سازنده نشان داده شده است.
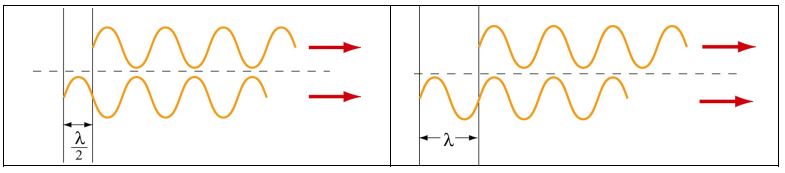
بهمنظور شناسایی محل دقیق نوارها علاوه بر فرض ، فاصله بین دو شکاف نیز باید بیشتر از طول موج در نظر گرفته شود. این فرض معادل با آن است که اندازه بسیار کوچک فرض شود. با این فرض اندازه این زاویه را میتوان برابر با رابطه زیر تقریب زد.
با قرار دادن رابطه فوق در مربوط به امواج سازنده و ویرانگر موقعیتهای نوارهای روشن و تاریک بهترتیب برابر میشوند با:
موقعیتهای نوارهای تاریک نیز برابرند با:
مثال
مشخصههای هندسی مربوط به یک آزمایش دو شکاف را مطابق با اندازههای زیر در نظر بگیرید.
با این فرضیات:
- اختلاف مسیر برای امواجی که به نقطه میرسند، را بهدست آورید.
- اندازه این اختلاف را بر حسب بدست آورید.
- نقطه نشاندهنده نوار روشن یا تاریک است؟
(a): همانطور که در بالا نیز بیان شد، اختلاف مسیر مطابق با رابطه بدست میآید. در حالتی که است، کوچک بوده و میتوان از تقریب استفاده کرد. از این رو اندازه اختلاف مسیر برابر میشود با:
(b): با توجه به پاسخ بدست آمده در قسمت (a) نسبت اختلاف فاصله به طول موج نیز برابر میشود با:
بنابراین است.
(c): با توجه به این که اختلاف فاصله مضربی صحیح از طول موج است، شدت موج در نقطه ماکزیمم بوده و نوار مربوط به آن بهصورت روشن است.
در صورتی که مطلب فوق برای شما مفید بوده است، آموزشهای زیر نیز به شما پیشنهاد میشوند:













هم این مقاله و مقاله فوتون بسیار خوب بود
بسیارزیبا مطالب تازه یادگرفتم سپاس برا