تحلیل واریانس با داده های تکراری — پیاده سازی در پایتون

یکی از معمول و محبوبترین روشهای تحلیل داده در روانشناسی و علوم اجتماعی، «تحلیل واریانس بین آزمودنیها» (Within-Subjects Designs) است. این شیوه از تحلیل، توسط تکنیک آنالیز واریانس با مقدارهای تکراری (Repeated Measures ANOVA) قابل اجرا و پیادهسازی است. در این نوشتار به بررسی این شیوه از تحلیل دادهها خواهیم پرداخت و برای انجام محاسبات مربوطه نیز از زبان برنامهنویسی پایتون و کتابخانههای آن کمک خواهیم گرفت. تحلیل واریانس با داده های تکراری در پایتون توسط کتابخانه pyvttble قابل پیادهسازی است که در این نوشتار به معرفی و کارکرد این کتابخانه نیز پرداخته خواهد شد.
البته قبل از هر چیز به مفاهیم اولیه و نظری در مورد تحلیل واریانس با داده های تکراری که گاهی تحلیل واریانس بین آزمودنیها نیز گفته میشود، پرداختهایم. این شیوه محاسبه اولین با توسط دانشمند و محقق بزرگ آمار «رونالد فیشر» (Ronald Fisher) پایهریزی شد و بعدها توسعه یافته و کاربردهای زیادی پیدا کرد.
برای آگاهی از مفاهیم اولیه در تحلیل واریانس به مطلب تحلیل واریانس (Anova) — مفاهیم و کاربردها و برای آشنایی با روشهای رگرسیونی به رگرسیون خطی چندگانه (Multiple Linear Regression) — به زبان ساده مراجعه کنید. همچنین اطلاع از شیوه محاسبات مربوط به رگرسیون خطی که در مطلب رگرسیون خطی — مفهوم و محاسبات به زبان ساده و هم خطی در مدل رگرسیونی — به زبان ساده قابل مطالعه است، خالی از لطف نیست.

تحلیل واریانس با داده های تکراری
برای محاسبه و تحلیل واریانس با داده ای تکراری در پایتون، از این جهت کتابخانه pyvttbls را انتخاب کردهایم که توسط آن قادر به ایجاد جدولهای محوری چند بُعدی (Multidimensional Pivot Table) هستیم. همچنین انجام آزمونهای متنوع آماری از دیگر ویژگیهای این بسته یا کتابخانه محسوب میشود. به این ترتیب انجام تحلیل واریانس با استفاده از یک چارچوب داده (DataFrame) در پایتون امکانپذیر میشود. البته این کتابخانه نسخه جدید یا ارتقاء یافته نداشته و برای اجرای آن نیز احتیاج است که کتابخانه قدیمی Numpy را روی پایتون نصب کرده باشید.
تحلیل واریانس درون آزمودنیها
قبل از هر چیز بهتر است در مورد تحلیل واریانس درون آزمودنی اطلاعات بیشتری کسب کنیم. البته میدانیم که در این حالت در هر گروه برای هر آزمودنی بیش از یک مشاهده وجود دارد و استفاده از خصوصیات آنها در دقت محاسبات و نتیجهگیری آماری تاثیر گذار است. در نوشتار دیگری از فرادرس با عنوان تحلیل واریانس یک طرفه در پایتون --- راهنمای گام به گام با نحوه اجرای تحلیل واریانس بین آزمودنیها (Between Subjects) آشنا شدیم. مشخص است که در آنجا هدف تشخیص تمایز بین گروهها بود. با اینکه در تحلیل واریانس درون آزمودنی نیز هدف تشخیص اختلاف بین گروهها است ولی در این شکل از تحلیل واریانس، هر آزمودنی (نمونه تصادفی) در هر یک از حالتها یا تیمارها شرکت داده میشود و مقدار مورد نظر برایشان اندازه گرفته خواهد شد.
در نتیجه به نظر میرسد مقادیر تکراری برای هر آزمودنی در اختیارمان قرار گرفته است. در حالیکه در تحلیل واریانس بین آزمودنیها، برای هر گروه نمونههای تصادفی جداگانهای تهیه شده و تیمارها برای گروههای مجزا صورت میگیرد و هر آزمودنی فقط در یک یا حداکثر چند تیمار دخالت داده میشود؛ از سوی دیگر در تحلیل واریانس درون آزمودنی، این کار برای همه تیمارها در بین آزمودنیها صورت میگیرد. به این ترتیب شاید بتوان یکی از مزایای استفاده از تحلیل واریانس درون آزمودنی را، استفاده از حجم نمونه کوچکتر نسبت به تحلیل واریانس بین آزمودنیها دانست بدون آنکه توان آزمون (Test Power) کاهش یابد. به این ترتیب در هزینههای نمونهگیری و جمعآوری اطلاعات صرفهجویی زمانی و ریالی زیادی میشود.
از طرف دیگر، پراکندگی مربوط به مشاهدات از جمله خطا، خارج میشود چون یک آزمودنی در بیش از یک تیمار به کار رفته است و به این ترتیب هر آزمودنی با مقدار کنترل خودش مقایسه میشود و اثر خطای عوامل خارجی و غیرقابل کنترل که در ابتدای طرح نیز در نظر گرفته نشده بود، در میزان پراکندگی مشاهدات کاهش مییابد. در نتیجه به نظر میرسد که دقت نیز برای مشخص کردن تغییرات بین گروهها افزایش خواهد یافت.
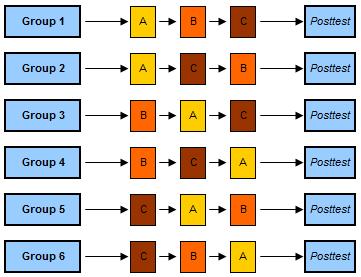
تحلیل واریانس با مقدارهای تکراری (بین آزمودنی) به کمک پایتون
با توجه به توضیحات گفته شده، ابتدا باید کتابخانه pyvttbl را نصب و راهاندازی کنیم. دستور زیر به این منظور نوشته شده است.
1
2pip install pyvttblحال به نحوه کدنویسی و انجام این تحلیل به کمک یک فایل اطلاعاتی فرضی میپردازیم. این دادهها از یک توزیع نرمال با میانگینهای متفاوت و واریانس ثابت (scale=112) تولید شدهاند. کدی که در ادامه مشاهده میکنید به منظور تولید این مجموعه داده نوشته شده است. این اطلاعات در یک چارچوب اطلاعاتی به نام df از نوع pyvttbl قرار گرفتهاند. مجموعه داده های تولید شده زمان پاسخ آزمودنیها به یک محرک را در دو وضعیت شلوغی و سکوت اندازهگیری کرده است. متغیر وضعیت (Condition) بیانگر این دو حالت بوده و متغیر rts نیز زمان پاسخ به این محرک را نشان میدهد. قرار است متوجه شویم که زمان پاسخ با توجه به نوع وضعیت تفاوت دارد یا خیر. به بیان دیگر آیا زمان پاسخ در محیط ساکت کوتاهتر از مدت پاسخ در محیط شلوغ است؟
نکته: چارچوب اطلاعاتی تولید شده توسط کتابخانه pyvttble به صورت یک جدول محوری است و با دیگر چارچوبهای اطلاعاتی (dataframe) در پایتون متفاوت است. برای انجام این آزمایش ۴۰ مشاهده در نظر گرفته شدهاند که در دو وضعیت شلوغی و سکوت زمان پاسخگویی آنها اندازهگیری شده است. مرکز توزیع نرمال برای داده های مربوط به محیط شلوغ به صورت مضربی از زمان پاسخ rts*N تعیین شده.
1from numpy.random import normal
2import pyvttbl as pt
3from collections import namedtuple
4
5N = 40
6P = ["noise","quiet"]
7rts = [998,511]
8mus = rts*N
9
10Sub = namedtuple('Sub', ['Sub_id', 'rt','condition'])
11df = pt.DataFrame()
12for subid in xrange(0,N):
13 for i,condition in enumerate(P):
14 df.insert(Sub(subid+1,
15 normal(mus[i], scale=112., size=1)[0],
16 condition)._asdict())انجام تحلیل واریانس با اندازههای تکراری با pyvttbl بسیار ساده است. کافی است که یک مجموعه داده توسط کتابخانه DataFrame ایجاد کرده و با کمک دستور anova آن را مورد تحلیل قرار دهید. کد مربوط به این تحلیل در ادامه دیده میشود.
1aov = df.anova('rt', sub='Sub_id', wfactors=['condition'])
2print(aov)اولین پارامتر، در این تابع متغیر وابسته شما (به عنوان مثال زمان پاسخ) است و پارامتر sub نیز ستونهای مربوط به شماره یا شناسه آزمودنیها را نشان میدهد. در انتها نیز پارامتر wfactors نیز تیمارهای درون آزمودنیها را مشخص میکند. در حقیقت این قسمت شامل اسامی ستونهایی است که بیانگر عاملها یا همان متغیر تیمار درون آزمودنیها است. در دادههای شبیهسازی شده، فقط یک تیمار به نام condition با دو سطح مقدار quiet و noise وجود دارد.
نکته: از آنجایی که این کتابخانه قدیمی است، لازم است که کتابخانه Numpy با نسخه حداکثر 1.1 را نصب داشته باشید. در غیر اینصورت ممکن است با پیغام خطای unsupported operand type(s) for +: ‘float’ and ‘NoneType’ مواجه شوید. پس بهتر است کتابخانه Numpy را به نسخههای قدیمی برگردانید.
حاصل اجرای این دستورات به صورت خروجی زیر خواهد بود:
| ... | Sig | F | MS | df | Type III Sum of Squares | Source | |||
| 4.165 | 0.000 | 309.093 | 4209536.428 | 1.000 | - | 4209536.428 | Sphericity Assumed | condition | |
| 4.165 | 0.000 | 309.093 | 4209536.428 | 1.000 | 1.000 | 4209536.428 | Greenhouse-Geisser | ||
| 4.165 | 0.000 | 309.093 | 4209536.428 | 1.000 | 1.000 | 4209536.428 | Huynh-Feldt | ||
| 4.165 | 0.000 | 309.093 | 4209536.428 | 1.000 | 1.000 | 4209536.428 | Box | ||
| 13618.991 | 39.000 | - | 531140.646 | Sphericity Assumed | Error(condition) | ||||
| 13618.991 | 39.000 | 1.000 | 531140.646 | Greenhouse-Geisser | |||||
| 13618.991 | 39.000 | 1.000 | 531140.646 | Huynh-Feldt | |||||
| 13618.991 | 39.000 | 1.000 | 531140.646 | Box |
همانطور که در جدول خروجی دیده می شود، مجموع مربعات مورد استفاده، از نوع (Type III) است که همان جدولی است که نرمافزار آماری رایج مانند SPSS یا SAS در هنگام محاسبه آماره F یا F-Statistics در تحلیل واریانس (ANOVA) ارائه مینمایند. همچنین در این جدول اجزایی دیگری با توجه به فرضیه کروی بودن دادهها (ثابت بودن واریانس درون گروهی) قابل مشاهده است. مشخص است که مقدار مربع که معیاری برای اندازه اثر است، برای هر تیمار یا عامل اندازهگیری شده است. در اینجا به وضوح دیده میشود که مقدار Sig تقریبا برابر با صفر است که بیانگر اثر متغیر وضعیت (Condition) روی زمان پاسخگویی است.
اگر لازم باشد که دادهها را تبدیل کنید کافی است که از پارامتر transform در این دستور استفاده کنید. این تبدیل میتواند به چند صورت انجام شود. تبدیلاتی نظیر log یا log10، معکوس، ریشه دوم یا همان جذر یا arcsin و windsor10 قابل استفاده هستند. به عنوان مثال، اگر میخواهید از تبدیل log استفاده کنید، فقط کافی است آرگومان تبدیل را به صورت "log "به دستور اضافه کنید. هر یک از روشهای ذکر شده در بالا میتواند به عنوان آرگومان در قالب یک رشته متنی مورد استفاده قرار گیرد.
1ovlog = df.anova('rt', sub='Sub_id', wfactors=['condition'], transform='log')در انتها نیز تابعی برای محاسبه آماره F و میانگین مربعات خطا، eta () مربع تعمیم یافته و محاسبه مقدار احتمال تهیه کردهایم. این تابع عاملها و خروجی تحلیل واریانس را گرفته و محاسبات را انجام میدهد.
1def extract_for_apa(factor, aov, values = ['F', 'mse', 'eta', 'p']):
2 results = {}
3 for key,result in aov[(factor,)].iteritems():
4 if key in values:
5 results[key] = result
6
7 return resultsاگر بخواهید آنچه در خروجی ظاهر میشود را در صفحات وب و با قالب HTML نمایش دهید، لازم است برنامه زیر را نیز اجرا کرده و توسط آن نتایج را نمایش دهیم.
1import SimpleHTML
2output = SimpleHTML.SimpleHTML('Title of your HTML-table')
3aov._within_html(output)
4output.write('results_aov.html')جمعبندی و خلاصه
در این نوشتار، ابتدا به مفاهیم اولیه تجزیه و تحلیل واریانس با مقدارهای تکراری پرداختیم و مزایای استفاده از آن را بازگو کردیم. سپس با استفاده از بعضی توابع و کتابخانههای پایتون، تحلیل واریانس با مقدارهای تکراری را برای یک مجموعه داده فرضی انجام دادیم. به نظر میرسد که نتایج حاصل (یعنی وجود فاصله بین دو تیمار) مورد آزمون قرار گرفته و بیاثر بودن محیط یا شرایط (Condition) در زمان پاسخگویی با توجه به p-value های کوچک در سطح خطای 0.05 رد میشود.
اگر مطلب بالا برای شما مفید بوده است، آموزشهای زیر نیز به شما پیشنهاد میشوند:
- مجموعه آموزش های SPSS
- مجموعه آموزشهای داده کاوی یا Data Mining در متلب
- مجموعه آموزشهای آمار و احتمالات
- آموزش همبستگی و رگرسیون خطی در SPSS
- رگرسیون خطی — مفهوم و محاسبات به زبان ساده
- تحلیل واریانس (Anova) — مفاهیم و کاربردها
- رگرسیون خطی چندگانه (Multiple Linear Regression) — به زبان ساده
^^












