انحراف معیار چیست؟ – به زبان ساده با مثال

امروزه دادهها، نقش مهمی را در علم و زندگی روزمره ایفا میکنند. این دادهها ممکن است حاوی اطلاعاتی در مورد سن، میزان تحصیلات، ضریب هوشی، نمره و بسیاری از اطلاعات دیگر در مورد افراد جوامع مختلف یا در مورد تصاویر دریافتی از تلسکوپ جیمز وب یا نتایج آزمایشی مهم در شیمی باشند. برای جمعآوری دادههای مختلف باید از کل جمعیت جامعه آماری یا قسمتی از جمعیت استفاده شود. پس از جمعآوری دادهها، دادهکاوی روی آنها آغاز میشود. بر روی دادههای آماری جمعآوری شده، عملیات مختلفی را میتوان انجام داد و کمیتهای مختلفی را محاسبه کرد. انحراف معیار یکی از این کمیتها است که در این مطلب در مورد آن صحبت خواهیم کرد و تلاش میکنیم به پرسش انحراف معیار چیست به زبانی ساده و گویا پاسخ دهیم.
با استفاده از انحراف معیار میتوانیم میزان پراکندگی دادهها را در مجموعهای از دادهها اندازه بگیریم. همچنین، با استفاده از آن میتوانیم فاصله هر متغیر از میانگین و متغیرهای دیگر را بهدست آوریم. در بیشتر موارد انحراف معیار با علامت نشان داده میشود. معاملهگران و تحلیلگران از این کمیت برای تعیین نوسانات و امنیت بازار استفاده میکنند. جذر واریانس، کمیت دیگری به نام انحراف معیار را به ما میدهد. در این مطلب از مجله فرادرس، ابتدا به پرسش انحراف معیار چیست به زبان ساده پاسخ میدهیم و با ذکر چند مثال ساده، با مفهوم آن آشنا میشویم. سپس، در مورد چگونگی محاسبه انحراف معیار در اکسل و پایتون با یکدیگر صحبت میکنیم.
انحراف معیار چیست ؟
انحراف معیار، پراکندگی دادههای اندازهگیری شده نسبت به مقدار میانگین دادهها را نشان میدهد. به بیان دیگر، انحراف معیار در مورد پراکندگی دادههای اندازهگیری شده صحبت میکند. به عنوان مثال، فرض کنید آزمونی چهارگزینهای متشکل از ۲۰ سوال دارید. پاسخهای شما به هر سوال، یکی از گزینههای ۱، ۲، ۳ یا ۴ است. انحراف معیار، پراکندگی پاسخهای شما به ۲۰ سوال را نشان میدهد.
مثال دیگری را با یکدیگر بررسی میکنیم. فرض کنید قد تعدادی از افراد را اندازه گرفتهاید. انحراف معیار به ما میگوید قد افراد چگونه حول مقدار میانگین پراکنده شده است. بنابراین، ابتدا باید مقدار میانگین قدِ افراد را اندازه بگیریم. برای محاسبه میانگین قد افراد در گروه تعیین شده، قدِ تمام آنها را با یکدیگر جمع و بر تعداد افراد گروه تقسیم میکنیم:
فرض کنید تعداد افراد گروه، پنج نفر و میانگین قد آنها برابر ۱۷۷/۸ سانتیمتر است.

اکنون میخواهیم بدانیم، قد هر فرد چگونه از مقدار میانگین قدی تفاوت دارد.
- فرد شماره یک، ۰/۲ سانتیمتر از مقدار میانگین بلندتر است.
- فرد شماره دو، ۲/۸ سانتیمتر از مقدار میانگین کوتاهتر است.
- فرد شماره سه، ۱۴/۸ سانتیمتر از مقدار میانگین کوتاهتر است.
- فرد شماره چهار، ۱۵/۲ سانتیمتر از مقدار میانگین بلندتر است.
- فرد شماره پنج، ۲/۳ سانتیمتر از مقدار میانگین بلندتر است.
همانطور که مشاهده میکنیم، اختلاف قد فرد شماره سه و چهار نسبت به مقدار میانگین، نسبت به افراد دیگر بیشتر است. ما علاقهمند به تفاوت قد هر فرد نسبت به مقدار میانگین قدی نیستیم، بلکه میخواهیم بدانیم قدِ هر فرد به طور میانگین چه مقدار با مقدار میانگین قدی تفاوت دارد. بنابراین، قد این افراد به صورت میانگین، چه مقدار با میانگین قدی آنها متفاوت است؟ به بیان دیگر، به طور متوسط قد افراد چه مقدار با ۱۷۷/۸ سانتیمتر تفاوت دارد؟ برای پاسخ به این پرسش از انحراف معیار استفاده میکنیم. در این مثال، میانگین انحراف قدی افراد از مقدار میانگین برابر ۹/۶۳ سانتیمتر است. چگونه میتوانیم انحراف معیار را بهدست آوریم؟ انحراف معیار با استفاده از رابطه ریاضی زیر بهدست میآید:
در رابطه فوق:
- : انحراف معیار است.
- n: تعداد افراد یا تعداد نمونه بررسی شده است.
- : مقدار هر نمونه است. به عنوان مثال، در مثال اندازهگیری قد، قد هر فرد را نشان میدهد.
- : مقدار میانگین را نشان میدهد.

از اینرو، برای محاسبه انحراف معیار، مراحل زیر را طی میکنیم:
- ابتدا، نمونه موردنظر را انتخاب میکنیم.
- دادههای لازم مربوط به هر نمونه را اندازه میگیریم.
- مقدار میانگین دادههای اندازهگیری شده را محاسبه میکنیم.
- داده اندازهگیری شده برای هر نمونه را از مقدار میانگین کم و مربع مقدار تفاضل را بهدست میآوریم.
- این کار را برای تمام نمونهها انجام و مقدارهای بهدست آمده را با یکدیگر جمع میکنیم.
- مقدار بهدست آمده از مرحله ۵ را بر تعداد نمونهها تقسیم میکنیم.
- از مقدار بهدست آمده از مرحله ۶ جذر میگیریم و انحراف معیار را بهدست میآوریم.
تا اینجا فهمیدیم انحراف معیار چیست و چگونه محاسبه میشود. اکنون میتوانیم انحراف معیار مثال قدِ پنج فرد را به راحتی محاسبه کنیم. مقدار میانگینِ قد افراد برابر ۱۷۷/۸ سانتیمتر است. با جایگزینی قد هر فرد و میانگین قدی در فرمول انحراف معیار داریم:
بنابراین، انحراف معیار را میتوانیم به صورت جذرِ میانگین مجموعِ مربعِ تفاضل هر مقدار از مقدار میانگین، تعریف کنیم. محاسبه انحراف معیار مشابه محاسبه مقدار میانگین مجموعهای از دادهها است. به این نکته توجه داشته باشید که میانگین، انواع متفاوتی دارد. در حالت عادی، برای محاسبه مقدار میانگین، دادها را با یکدیگر جمع و حاصل بهدست آمده را بر تعداد نمونهها، تقسیم میکنیم. اما در محاسبه انحراف معیار، «میانگین مربعی» (Quadratic Mean) را بهدست میآوریم:
اگر در محاسبه انحراف معیار به جای رابطه فوق، از رابطه معمولِ میانگین، یعنی استفاده میکردیم، مقدار صفر بهدست میآمد. توجه به این نکته مهم است که انحراف معیار را میتوان با استفاده از دو فرمول بهدست آورد. فرمول اول را در مطالب بالاتر نوشتیم:
فرمول دوم نیز به صورت زیر نوشته میشود:
تفاوت دو فرمول در چیست؟ در فرمول اول، مجموع مربع تفاضل از میانگین بر تعداد کل نمونهها، n، اما در فرمول دوم، مجموع مربع تفاضل از میانگین بر تعداد کل نمونهها منهای یک، n-1، تقسیم میشود. چرا دو رابطه برای محاسبه انحراف معیار وجود دارند؟ محاسبه انحراف معیار برای تعداد زیادی نمونه، یکی از محاسبات مهم در آمار است. به عنوان مثال، فرض کنید که میخواهید انحراف معیارِ سنی تمام استادهای دانشگاه در سراسر ایران را بهدست آورید. اگر سنِ تمام اساتید دانشگاه در ایران را بدانیم، از رابطه برای محاسبه انحراف معیار استفاده میکنیم. اما گاهی نمیتوانیم مطالعه آماری خود را روی تمام جمعیت موردنظر انجام دهیم.
بنابراین، تعدادی استاد را به عنوان نمونه آماری انتخاب و از این جامعه آماری انتخاب شده برای تخمین انحراف معیار سنِ تمام استادهای دانشگاههای سراسر ایران و از رابطه برای محاسبه مقدار آن استفاده میکنیم.
تفاوت واریانس و انحراف معیار چیست ؟
برای پاسخ دقیقتر به پرسش انحراف معیار چیست باید تفاوت آن را با واریانس بدانیم. برای آنکه بدانیم تفاوت واریانس و انحراف معیار چیست، ابتدا واریانس را به صورت خلاصه تعریف میکنیم.
واریانس چیست؟
واریانس به ما میزان پراکندگی دادههای آماری جمعآوری شده یا به بیان دیگر، واریانس اطلاعاتی را در مورد میزان تغییر مقدار دادههای آماری به ما میدهد. هرچه مقدار واریانس بزرگتر باشد، میزان پراکندگی و تغییر دادههای آماری نیز بیشتر خواهد بود. واریانس با استفاده از رابطه زیر بهدست میآید:
در نتیجه، برای محاسبه واریانس، ابتدا مقدار انحراف معیار را بهدست میآوریم، سپس آن را به توان دو میرسانیم. اکنون میتوانیم در مورد تفاوتهای انحراف معیار و واریانس با یکدیگر صحبت کنیم:
- با استفاده از انحراف معیار میتوانیم مقدار فاصله اعداد را در مجموعه داده، اما با استفاده از واریانس، مقدار واقعی تفاوت اعداد از مقدار میانگین را در مجموعه داده بهدست میآوریم.
- انحراف معیار، جذر واریانس و یکای آن مشابه یکای دادهها در مجموعه داده است. واریانس میتواند به صورت مجذور یا درصد بیان شود (در دادههای مالی این مورد مطرح میشود).
- انحراف معیار میتواند از واریانس بزرگتر باشد، زیرا جذر اعداد اعشاری کوچکتر از یک از عدد اصلی بزرگتر خواهد بود. به عنوان مثال، جذر ۰/۱ در حدود ۰/۳ است.
- اگر واریانس از یک بزرگتر باشد، انحراف معیار کوچکتر خواهد بود.
حل نمونه سوال انحراف معیار
پس از پاسخ به پرسش انحراف معیار چیست و توضیح تفاوت آن با واریانس، سه مثال را با یکدیگر حل میکنیم.
مثال اول محاسبه انحراف معیار
در باغی، ۳۹ نوع گیاه وجود دارند. ارتفاع (برحسب سانتیمتر) ۵ گیاهی که به صورت تصادفی انتخاب شدهاند برابر ۳۸، ۵۱، ۴۶، ۷۹ و ۵۷ سانتیمتر است. انحراف معیار ارتفاع گیاهان چه مقدار است؟

پاسخ
برای بهدست آوردن انحراف میانگین، مرحلههای زیر را طی میکنیم:
- مقدار میانگین دادههای آماری را بهدست میآوریم.
- تفاضل مقدار هر نمونه را از میانگین محاسبه و حاصل را به توان دو میرسانیم. این کار را برای تمام نمونهها انجام میدهیم.
- سپس، مربع تفاضلها را با یکدیگر جمع و بر تعداد نمونهها تقسیم میکنیم.
- در پایان، از حاصل کل، جذر میگیریم.
۵ گیاه از بین ۳۹ گیاه موجود در باغ را به صورت تصادفی انتخاب میکنیم و ارتفاع آنها را اندازه میگیریم. میانگین ارتفاع این پنج گیاه برابر است با:
برای انحراف معیار از رابطه زیر استفاده میکنیم:
چرا در رابطه فوق، مجموع مربع تفاضلها بر و نه تقسیم شده است؟ دلیل این موضوع آن است که ارتفاع ۳۹ گیاهِ در باغ را نداریم. بلکه، پنج گیاه را به صورت تصادفی انتخاب کردهایم و ارتفاع آنها را اندازه گرفتهایم. به بیان دیگر، به جای کار روی کل جمعیت گیاهان باغ، چند نمونه را به صورت تصادفی انتخاب کردهایم. در نتیجه، مجموع مربع تفاضلها را بر تقسیم میکنیم.
مثال دوم محاسبه انحراف معیار
۵ گوریل به صورت تصادفی از بین ۲۹ گوریل انتخاب شدهاند. سن گوریلهای انتخاب شده برابر ۸، ۴، ۱۴، ۱۶ و ۸ سال است. مقدار متوسط سن گوریلها چه مقدار است؟ مقدار انحراف معیار را بهدست آورید.

پاسخ
۵ گوریل به صورت تصادفی از بین ۲۹ گوریل انتخاب شدهاند. بنابراین، به جای بررسی جمعیت کلِ گوریلها، روی مجموعه انتخاب شده از آنها کار میکنیم. در نتیجه، برای محاسبه انحراف معیار از رابطه زیر استفاده میکنیم:
مقدار میانگینِ سنی ۵ گوریل برابر است با:
در ادامه، تفاضل مقدار هر نمونه را از میانگین، محاسبه و حاصل را به توان دو میرسانیم. این کار را برای تمام نمونهها انجام میدهیم. سپس، مربع تفاضلها را با یکدیگر جمع و بر تعداد نمونهها تقسیم میکنیم. محاسبات انجام شده در جدول زیر نوشته شده است.
| سن گوریل | تفاضل مقدار سن هر گوریل از میانگین سنی | مربع تفاضل |
| ۸ | ||
| ۴ | ||
| ۱۴ | ||
| ۱۶ | ||
| ۸ | 4 |
به این نکته دقت داشته باشید که ما میانگین سنی ۲۹ گوریل را نداریم و تنها میانگی سنی ۵ گوریل را میدانیم. سن هر یک از ۵ گوریلِ انتخاب شده در مقایسه با سنِ بقیه گوریلها با احتمال بیشتری به میانگین بهدست آمده، ۱۰ سال، نزدیکتر است. از اینرو، انحراف معیار محاسبه شده ممکن است انحراف واقعی از میانگین سنی جمعیت تمام گوریلها را به درستی نشان ندهد. برای جبران، مجموع تفاضل مربعات را به جای n بر تقسیم میکنیم.
از آنجا که ۵ گوریل به صورت تصادفی انتخاب شدهاند، مقدار n برابر ۵ است:
مثال سوم محاسبه انحراف معیار
سن ۶ شیر در باغ وحشی محلی برابر ۱۳، ۲، ۱، ۵ ،۲ و ۷ سال است. مقدار متوسط سن شیرها چه مقدار است؟ مقدار انحراف معیار را بهدست آورید.

پاسخ
در این مثال، برخلاف مثال دوم، سن تمام شیرها را داریم، بنابراین جمعیت کل شیرهای داخل باغ وحش را بررسی میکنیم. در نتیجه، برای محاسبه انحراف معیار از رابطه زیر استفاده میکنیم:
مقدار میانگینِ سنی ۶ شیر برابر است با:
در ادامه، تفاضل مقدار هر نمونه را از میانگین، محاسبه و حاصل را به توان دو میرسانیم. این کار را برای تمام نمونهها انجام میدهیم. سپس، مربع تفاضلها را با یکدیگر جمع و بر تعداد نمونهها تقسیم میکنیم. محاسبات انجام شده در جدول زیر نوشته شده است.
| سن شیر | تفاضل مقدار سن هر شیر از میانگین سنی | مربع تفاضل |
| ۱۳ | ||
| ۲ | ||
| ۱ | ||
| ۵ | ||
| ۲ | 4 | |
| ۷ |
در این مثال، اطلاعات مربوط به سن تمام شیرها را داریم، بنابراین، میانگین بهدست آمده برای کلِ جمعیت و نه قسمتی از آنها است. در نتیجه، برای محاسبه انحراف معیار، مجموع تفاضل انحراف از میانگین را بر تعداد کل نمونهها تقسیم میکنیم.
جمعیت کل شیرها در باغ وحش برابر ۶ است، بنابراین داریم:
تا اینجا فهمیدیم انحراف معیار چیست و چگونه محاسبه میشود. برای محاسبه انحراف معیار باید به این نکته توجه داشته باشیم که آیا انحراف معیار کلِ جمعیت را بهدست میآوریم یا انحراف معیار تعدادی نمونه از جمعیت کل را محاسبه میکنیم. همچنین، توجه به این نکته مهم است که چگونگی محاسبه انحراف معیار به نوع داده اندازهگیری شده بستگی دارد. توزیع دادهها به معنای انحراف آنها از مقدار میانگین است. دادهها به دو گروه دادههای گروهبندی شده و دادههای گروهبندی نشده تقسیم میشوند. در ادامه این مطلب از مجله فرادرس، ابتدا این دو گروه از دادهها را تعریف میکنیم. سپس، در مورد محاسبه انحراف معیار برای انواع دادهها توضیح میدهیم.
انواع داده ها در محاسبه انحراف معیار چیست؟
در پاسخ به پرسش انحراف معیار چیست، آن را به صورت میزان پراکندگی دادهها تعریف کردیم. جمعآوری دادهها، نخستین گام در انجام پژوهشهای مختلف است. پس از جمعآوری دادهها باید راههای مناسبی برای تراکم و مرتب کردن دادهها، برای بررسی ویژگیهای آنها بهدست آوریم. دادهها به شکل اصلی خود و بلافاصله پس از جمعآوری به عنوان دادههای گروهبندی نشده شناخته میشوند. به بیان ساده، دادههای خام یا گروهبندی نشده، فهرستی از اعداد هستند که چیزی را نمایش نمیدهند. در مقابل، دادههای گروهبندی شده به دادههایی گفته میشود که در کلاسها و دستههای مختلف در کنار یکدیگر قرار میگیرند.
داده گروه بندی نشده چیست؟
به دادههای عددی به شکل اصلی خود، دادههای گروهبندی نشده گفته میشود. این دادهها، مجموعهای از مشاهدات جمعآوری شده در مدت پژوهش یا برگرفته از منبعی مشخص هستند. این دادهها معمولا به عنوان مشاهدات فردی، به صورت جدول یا محدودهای از مقادیر درهمریخته جمعآوری شدهاند. از آنجا که دادهها به شکل واقعی و اصلی خود ارائه میشوند، محاسبه، تجزیه و تحلیل و تفسیر آنها فرایندی سخت و وقتگیر خواهد بود. بنابراین، کسی نمیتواند به استفاده از این دادهها به نتیجه منطقی برسد، مگر آنکه دادهها با ترتیبی مشخص مرتب شده باشند.

به عنوان مثال، گاهی با چیدن دادهها به صورت نزولی یا صعودی میتوان اطلاعات مفیدی از آنها بهدست آورد. فرض کنید محدوده سنی کارمندان خانم در شرکتی به صورت زیر است:
دادههایی به این شکل، دادههای خام هستند. برای آنکه بدانیم چه تعداد خانم زیر ۳۵ سال هستند، میتوانیم از دادههای فوق استفاده کنیم. اما استفاده از آنها برای بهدست آوردن اطلاعات مفید کمی دستوپاگیر است. بنابراین، دادههای فوق را به صورت صعودی و از کمترین به بیشترین سن مرتب میکنیم:
به دادههای مرتب شده در بالا، دادههای مرتب شده گفته میشود. همچنین، تفاضل بین بیشترین و کمترین مقدار، محدوده دادهها را مشخص میکند. کار با دادههای زیاد حوصلهسربر و وقتگیر است. در بیشتر مواقع، برای راحتی کار و داشتن درک بهتری از دادههای جمعآوری شده آنها را در جدولی به نام جدول فراوانی مینویسیم. این جدول از دو ستون تشکیل شده است. در ستون اول داده موردنظر و در ستون دوم، تعداد داده نوشته میشود. به عنوان مثال، از میان خانمهای کارمند، سه خانم ۳۵ ساله هستند. از اینرو، تعداد داده ۳۵ و فراوانی آن برابر سه است.
داده گروه بندی شده چیست؟
به دادههای خام و اولیهای که در گروهها و دستههای مشخصی قرار میگیرند، دادههای گروهبندی شده میگویند. این کار را برای بهدست آوردن شکل فشردهتری از دادهها انجام میدهیم. دادهها زمانی گروهبندی میشوند که:
- متغیر در محدوده وسیعی قرار میگیرد.
- تعداد مشاهدات بسیار زیاد است.
- مرتب کردن دادهها زمانبر است.
به تعداد دفعاتی که مقدارهای متفاوت در گروههای مختلف وجود دارند، توزیع فرکانس گروه بندی شده گفته میشود. دادههای گروهبندی شده به دو دسته کلی دادههای گسسته و پیوسته تقسیم میشوند.
انواع روش های محاسبه انحراف معیار چیست ؟
تا اینجام میدانیم انحراف معیار چیست و چگونه با استفاده از روش میانگین واقعی محاسبه میشود. اما این روش، تنها روش محاسبه انحراف معیار نیست، بلکه با توجه به نوع دادهها و گسسته یا پیوسته بودن آنها، روشهای مختلفی برای محاسبه انحراف معیار وجود دارند. همانطور که در بخش قبل اشاره کردیم، دادهها به دو گروه کلی دادههای گروهبندی شده و گروه بندی نشده تقسیم میشوند. در ادامه، ابتدا محاسبه انحراف معیار در دادههای گروهبندی نشده و سپس دادههای گروهبندی شده را توضیح میدهیم.
محاسبه انحراف معیار داده های گروه بندی نشده
سه روش کلی برای محاسبه انحراف معیارِ دادههای گروهبندی نشده وجود دارند:
- روش میانگین
- روش میانگین فرضی
- روش انحراف گام
روش میانگین واقعی در محاسبه انحراف معیار چیست ؟
در مطالب بالا، به صورت مفصل در مورد این روش و فرمولهای محاسبه انحراف معیار با استفاده از این روش صحبت کردیم. در این روش، ابتدا مقدار میانگین دادهها را بهدست میآوریم. سپس، تفاضل هر داده از مقدار میانگین را محاسبه میکنیم و مقدار بهدست آمده را به توان دو میرسانیم. در ادامه، این کار را برای تمام دادهها انجام میدهیم، مقدارهای بهدست آمده را با یکدیگر جمع و بر تعداد نمونهها تقسیم میکنیم و در پایان جذر آن را بهدست میآوریم.

روش میانگین فرضی در محاسبه انحراف معیار چیست ؟
اگر مقدارهای بزرگ باشند، مقداری دلخواه به نام A برای میانگین دادهها انتخاب میشود، زیرا محاسبه میانگین برای دادههای بزرگ، سخت است. سپس، تفاضل و A را به صورت بهدست میآوریم. در پایان، انحراف معیار را با استفاده از رابطه زیر محاسبه میکنیم:
روش انحراف گام در محاسبه انحراف معیار چیست ؟
انحراف معیار دادههای گروهبندی شده را نیز میتوانیم با استفاده از این روش بهدست آوریم. در این روش نیز مقدار دلخواهی را به عنوان میانگین فرضی انتخاب و تفاضل تمام دادهها و A را به صورت d = x - A محاسبه میکنیم. در ادامه، انحراف گام، ی، را به صورت تقسیم d بر i بهدست میآوریم. i عامل مشترک تمام مقادیر d است. در پایان، انحراف معیار دادههای گروهبندی نشده با استفاده از روش انحراف گام با استفاده از رابطه زیر بهدست میآید:
n در رابطه فوق تعداد کل دادهها است.
محاسبه انحراف معیار داده های گروه بندی شده گسسته
تا اینجا میدانیم انحراف معیار چیست و با چه روشهایی برای دادههای گروهبندی نشده محاسبه میشود. در گروهبندی دادهها، مهمترین نکتهای که باید به آن توجه کنیم، ساخت توزیع فرکانس یا فراوانی است. همانند دادههای گروهبندی نشده، برای محاسبه دادههای گروهبندی شده نیز از سه روش زیر استفاده میکنیم:
- روش میانگین
- روش میانگین فرضی
- روش انحراف گام
محاسبه انحراف معیار داده های گسسته به روش میانگین واقعی
در مطالب بالا، محاسبه انحراف معیار را برای دادههای گروهبندی نشده توضیح دادیم. محاسبه انحراف معیار در دادههای گروهبندی شده نیز به صورت مشابه بهدست میآید، با این تفاوت که باید توزیع فراوانی را در نظر بگیریم. انحراف معیار مشاهدات و و ... تا با توزیع فراوانی و و ... تا با استفاده از فرمول زیر محاسبه میشود:
در رابطه فوق:
- n تعداد فرکانس یا تکرار و برابر است.
- مقدار میانگین دادهها است.
مثال محاسبه انحراف معیار به روش میانگین واقعی
انحراف معیار دادههای زیر را بهدست آورید.
| ۶ | ۲ |
| ۱۰ | ۳ |
| ۱۲ | ۴ |
| ۱۴ | ۵ |
| ۲۴ | ۴ |
ابتدا مقدار میانگین را بهدست میآوریم:
پس از محاسبه میانگین، جدول زیر را کامل میکنیم و واریانس را بهدست میآوریم.
| ۸/۲۲- | ۶۷/۵۷ | ۱۳۵/۱۴ |
| ۴/۲۲- | ۱۷/۸۱ | ۵۳/۴۳ |
| ۲/۲۲- | ۴/۹۳ | ۱۹/۷۲ |
| ۰/۲۲- | ۰/۰۴۸ | ۰/۲۴ |
| ۹/۷۸ | ۹۵/۶۵ | ۳۸۲/۶۰ |
محاسبه انحراف معیار داده های گسسته به روش میانگین فرضی
اگر مقدار دادههای گروهبندی شده گسسته بسیار بزرگ باشند، انحراف معیار را به صورت زیر محاسبه میکنیم:
- یکی از دادهها را به عنوان میانگین، انتخاب و آن را A مینامیم.
- سپس، تفاضل و A را به صورت بهدست میآوریم.
- در ادامه، مقدار d را در f، تعداد تکرار هر داده در گروه، ضرب و مجموع را محاسبه میکنیم.
- را محاسبه، مقدار آن را در f، تعداد تکرار هر داده در گروه، ضرب و مجموع را محاسبه میکنیم.
- مقدار انحراف معیار را با استفاده از فرمول زیر بهدست میآوریم:
در رابطه فوق:
- انحراف معیار است.
- N تعداد کل اندازهگیریها است.

مثال محاسبه انحراف معیار به روش میانگین فرضی
انحراف معیار دادههای زیر را با استفاده از روش میانگین فرضی بهدست آورید.
| اندازه () | فراوانی (f) |
| ۵ | ۶ |
| ۱۰ | ۷ |
| ۱۵ | ۳ |
| ۲۰ | ۲ |
| ۲۵ | ۱ |
| ۳۰ | ۱ |
ابتدا باید یکی از دادهها را به عنوان میانگین فرضی انتخاب میکنیم و آن را A مینامیم. در این مثال، را به عنوان میانگین فرضی انتخاب میکنیم. سپس، تفاضل و A را به صورت بهدست میآوریم. در ادامه، مقدار d را در f، تعداد تکرار هر داده در گروه، ضرب و مجموع را محاسبه میکنیم.
سپس، مجموع را بهدست میآوریم:
با قرار دادن و در رابطه ، مقدار انحراف معیار برابر ۶/۹ بهدست میآید.
محاسبه انحراف معیار داده های گسسته به روش انحراف گام
انحراف معیار دادههای گسسته گروهبندی شده را نیز میتوانیم با استفاده از این روش بهدست آوریم. روش انحراف گام، روشی است که برای بهدست آوردن میانگین مقدارهای بزرگ که قابلتقسیم بر عاملی مشترک هستند، استفاده میشود. به این نکته توجه داشته باشید که این روش گسترش یافته روش میانگین فرضی است. میانگین در این روش به صورت زیر محاسبه میشود:
در رابطه فوق:
- A میانگین فرضی است.
- h اندازه کلاس یا گروه است.
- برابر است.
- مقدار فراوانی برای هر داده است.
- برابر است.
- نقطه میانی هر بازه کلاسی است.
انحراف معیار نیز در این روش با استفاده از رابطه زیر بهدست میآید:
برای استفاده از این روش میتوانید به صورت زیر عمل کنید:
- جدولی متشکل از ۵ ستون به صورت زیر تهیه کنید:
- ستون یک: بازه کلاس
- ستون دو: نقطه میانی هر بازه کلاسی
- ستون سه: مقدار فراوانی برای هر داده
- ستون چهار: محاسبه به صورت
- ستون پنج: فراوانی هر داده یا
- میانگین را به صورت بهدست آورید.
- در پایان، مقدار میانگین را با اضافه کردن مقدار میانگین فرضی، A، به حاصلضرب عرض کلاس (h) در میانگینِ محاسبه کنید.
محاسبه انحراف معیار داده های گروه بندی شده پیوسته
اگر فراوانی دادهها پیوسته باشد، هر کلاسی با نقطه میانی خودش جایگزین میشود. پس از انجام این کار، انحراف معیار با روشهایی مشابه روشهای استفاده شده در توزیع فراوانی گسسته، بهدست میآید. نقطه میانی هر کلاس است. برای محاسبه آن بیشترین و کمترین مقدار داده در کلاس موردنظر را با یکدیگر جمع و حاصل را بر دو تقسیم میکنیم. به عنوان مثال، فرض کنید بازه کلاس از صفر تا ۱۰ تغییر میکند. برای بهدست آوردن نقطه میانی این بازه مقادیر صفر و ۱۰ را با یکدیگر جمع و حاصل بهدست آمده، یعنی ۱۰ را بر ۲ تقسیم میکنیم. در نتیجه، نقطه میانی کلاس یا گروه ۰ تا ۱۰ برابر ۵ است. پس از محاسبه نقطه میانی هر کلاس، انحراف معیار را میتوانیم با استفاده از فرمولهای گفته شده برای دادههای گروهبندی شده بهدست آوریم.
انحراف معیار متغیرهای تصادفی
در مطالب بالا فهمیدیم انواع روشهای وحاسبه انحراف معیار چیست. در این بخش، انحراف معیار متغیرهای تصادفی را با یکدیگر محاسبه میکنیم. با اندازهگیری پراکندگی توزیع احتمال متغیر تصادفی میتوانیم مقدار تفاوت متغیرهای با مقدار انتظاری را بهدست آوریم. این حالت تابعی است که به هر نتیجه در فضای نمونه، مقداری عددی اختصاص میدهد. متغیر تصادفی متغیری است که میتواند مقدارهای تصادفی و گسستهای داشته باشد. فرض کنید متغیر تصادفی و برابر تعداد تمرینهای انجام شده در طول یک هفته است. جدول زیر توزیع احتمال متغیر را نشان میدهد.
| ۰ | ۰/۱ |
| ۱ | ۰/۱۵ |
| ۲ | ۰/۴ |
| ۳ | ۰/۲۵ |
| ۴ | ۰/۱ |
همانطور که در جدول بالا مشاهده میکنید، تنها میتواند مقدارهای محدود مانند صفر، یک، دو، سه و چهار داشته باشد. از آنجا که مقدار محدود است، به آن متغیر تصادفی گسسته میگوییم. همچنین، مجموع برای مقدارهای از صفر تا چهار، برابر یک است. ابتدا، مقدار انتظاری یعنی را بهدست میآوریم. با محاسبه میتوانیم مقدار موردانتظار تمرین انجام شده در هفته را داشته باشیم. همچنین، در برخی موارد را همان مقدار میانگین میدانند.
چگونه محاسبه میشود. برای انجام این کار تعداد تمرینهای انجام شده در هر هفته را در احتمال انجام انها ضرب و با یکدیگر جمع میکنیم:
بنابراین، مقدار انتظاری تعداد تمرینهای انجام شده در هر هفته برابر ۲/۱ است. شاید از خود بپرسید، مقدارهای در جدول داده شده همه عدد صحیح هستند، چگونه میتوان ۲/۱ تمرین در هفته انجام داد؟ مقدار انتظاری بهدست آمده بدان معنا نیست که در یک هفته ۲/۱ تمرین انجام میدهید، بلکه با استفاده از آن میتوانیم نتیجه بگیریم که پس از گذشت ده هفته انتظار میرود ۲۱ تمرین انجام داده باشید. در ادامه، واریانس و انحراف معیار متغیر تصادفی را محاسبه میکنیم. برای محاسبه واریانس متغیر تصادفی مراحل زیر را طی میکنیم:
- تفاضل متغیر تصادفی و مقدار انتظاری را بهدست میآوریم.
- مربع تفاضل را بهدست میآوریم.
- حاصل مرحله دوم را در احتمال ضرب میکنیم.
- سه مرحله اول را برای تمام متغیرهای تصادفی محاسبه میکنیم.
- مقدارهای بهدست امده را با یکدیگر جمع میکنیم.
مقدار انحراف معیار متغیر تصادفی برابر جذر واریانس است و به صورت زیر محاسبه میشود:
اعداد بهدست آمده چه معنایی دارند؟ با توجه به جدول داده شده در بالا، با احتمال ۱۰ درصد هیچ تمرینی را در هفته انجام نمیدهید. با احتمال ۱۵ درصد یک تمرین، با احتمال ۴۰ درصد دو تمرین، با احتمال ۲۵ درصد ۳ تمرین و با احتمال ۱۰ درصد نیز ممکن است ۴ تمرین را در هفته انجام دهید. اگر عدد ۱/۰۹ را از مقدار انتظاری کم کنیم به یک و اگر به آن اضافه کنیم به سه نزدیک میشویم. این بدان معنا است که با احتمال زیادی شما بین یک تا ۳ تمرین را در هفته حل خواهید کرد.
مثال محاسبه انحراف معیار متغیر تصادفی
فردی برای درمان به بیمارستان مراجعه میکند. او برای درمان بیماری خود باید ۵۰۰ هزار تومان پول دارو پرداخت کند و پس از مصرف دارو با احتمال ۹۰ درصد بهبود مییابد. اگر داروهای تجویز شده سبب بهبود او نشوند، او بار دیگر باید به دکتر مراجعه کند و داروهای گرانتری با قیمت ۲ میلیون تومان مصرف کند. این فرد با مصرف این داروها به طور قطع درمان خواهد شد.

جدول زیر توزیع احتمال متغیر را نشان میدهد. مقدار کل پولی است که بیماری که به صورت تصادفی انتخاب شده است باید برای درمان کامل خود بپردازد. مقدار انحراف معیار را بهدست آورید.
| ۵۰۰ هزار تومان | ۹۰ درصد |
| ۲ میلیون و ۵۰۰ هزار تومان | ۱۰ درصد |
پاسخ
برای محاسبه انحراف معیار متغیر تصادفی مراحل زیر را طی میکنیم:
- تفاضل متغیر تصادفی و مقدار انتظاری را بهدست میآوریم.
- مربع تفاضل را بهدست میآوریم.
- حاصل مرحله دوم را در احتمال ضرب میکنیم.
- سه مرحله اول را برای تمام متغیرهای تصادفی محاسبه میکنیم.
- مقدارهای بهدست آمده را با یکدیگر جمع میکنیم.
- جذر عدد بهدست آمده در مرحله پنج را بهدست میآوریم.
ابتدا مقدار انتظاری یا میانگین را بهدست میآوریم:
مقدار انتظار بهدست آمده را در رابطه واریانس قرار میدهیم:
با جذر مقدار بهدست آمده، برابر ۶۰۰ هزار تومان بهدست میآید.
محاسبه انحراف معیار در اکسل
در مطالب بالا فهمیدیم انحراف معیار چیست. انحراف معیار، پراکندگی یا میزان انحراف دادهها از مقدار میانگین را نشان میدهد. به بیان دیگر، انحراف معیار به ما میگوید آیا دادههای به میانگین نزدیک هستند یا نوسان زیادی دارند. به کمک انحراف معیار میتوانیم به این نتیجه رسیم که آیا مقدار میانگین، به ما داده واقعی را میدهد یا خیر. هرچه انحراف معیار به صفر نزدیکتر باشد، تغییرات دادهها کمتر و مقدار میانگین، قابلاعتمادتر است. اگر انحراف معیار برابر صفر باشد، هر داده در مجموعه داده برابر مقدار میانگین است. در مقابل، هرچه مقدار انحراف معیار بزرگتر باشد، تغییرات دادهها و انحراف آنها از مقدار میانگین بیشتر و میانگین محاسبه شده دقت کمتری دارد.
برای آنکه بدانیم انحراف معیار چگونه کار میکند انحراف معیار و میانگین نمره درس زیستشناسی و ریاضی هفت دانشآموز در امتحان پایان ترم را بهدست میآوریم.
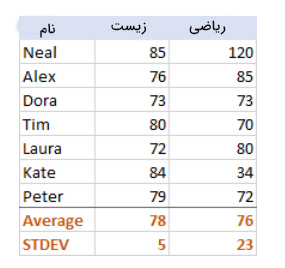
انحراف معیار نمرات زیست برابر ۵ است. این مقدار به معنی آن است که اختلاف بیشتر نمرههای درس زیست با مقدار میانگین بیشتر از ۵ نمره نیست. آیا این نشانه خوبی است؟ بله، این حالت نشان میدهد که نمرههای کسب شده توسط دانشآموزان در درس زیست تقریبا ثابت و یکنواخت است. اما نمرههای ریاضی اینگونه نیستند. انحراف معیار نمرههای درس ریاضی برابر ۲۳ است. این مقدار نشان میدهد که نمرههای کسب شده در درس ریاضی توسط دانشآموزان بسیار پراکنده است. بنابراین، کلاسی داریم که دانشآموزان آن در درس زیست تقریبا در یک سطح قرار دارند، اما در درس ریاضی با یکدیگر بسیار تفاوت دارند.
از انحراف معیار برای تحلیل کسبوکارهای مختلف و اندازهگیری ریسک سرمایهگذاری نیز استفاده میشود. هر چه مقدار انحراف معیار بزرگتر باشد، نوسانات بازدهی نیز بیشتر خواهد بود. برای محاسبه انحراف معیار باید به این نکته توجه داشته باشیم که آیا انحراف معیار کلِ جمعیت را بهدست میآوریم یا انحراف معیار تعدادی نمونه از جمعیت کل را محاسبه میکنیم. فرمول محاسبه هر یک از آنها در بالا نوشته شده است. برای محاسبه انحراف معیار در اکسل، شش تابع وجود دارند.
توابع محاسبه انحراف معیار نمونه در اکسل
برای محاسبه انحراف معیار تعدادی نمونه از جمعیت کل از رابطه استفاده میکنیم. برای محاسبه آن در اکسل نیز میتوانیم از دو تابع STDEV.S و STDEVA استفاده کنیم.
تابع STDEV در اکسل
تابع STDEV(number1,[number2],…) قدیمیترین تابع اکسل برای محاسبه انحراف معیار است. این تابع در اکسل ۲۰۰۳ تا اکسل ۲۰۱۹ وجود دارد. این تابع از اکسل ۲۰۰۷ به بعد میتواند بیش از ۲۲۵ آرگومان شامل اعداد و آرایهها را بپذیرد. تابع STDEV(number1,[number2],…) در اکسل ۲۰۰۳ تنها میتوانست تا ۳۰ آرگومان را بپذیرد.
نکته: تابع STDEV تابعی منسوخ شده است و در نسخههای جدیدتر اکسل، تنها برای سازگاری با نسخههای قدیمی نگه داشته شده است. اما هیچ تضمینی برای وجود این تابع در نسخههای اکسل که در آینده میآیند، وجود ندارد. بنابراین، توصیه میشود در نسخههای اکسل ۲۰۱۰ و بالاتر از تابع STDED.S به جای STDEV استفاده شود.
تابع STDEV.S در اکسل
تابع STDEV.S(number1,[number2],…) بهبود یافته تابع STDEV در اکسل است. تابع STDEV.S نیز انحراف معیار را براساس فرمولهای نوشته شده در بالا محاسبه میکند.
تابع STDEVA در اکسل
STDEVA(value1, [value2], …) نیز تابع دیگری برای محاسبه انحراف معیار در اکسل است. تفاوت این تابع با دو تابع گفته شده در بالا در چگونگی رفتار آن با متغیرهای منطقی و متنی است:
- تمام متغیرهای منطقی شمارش میشوند. فرقی ندارد که این متغیرها داخل آرایهها، داخل ارجاع به سلولهای اکسل یا به صورت مستقیم نوشته شده باشند. مهم آن است که تمام آنها توسط این تابع شمارش میشوند.
- متغیرهای متنی داخل آرایهها یا آرگومانها به عنوان صفر، اما نمایش متنی اعداد به صورت عددِ نمایش داده شده، شمارش میشوند.
- سلولهای خالی نادیده گرفته میشوند.
توابع محاسبه انحراف معیار جمعیت در اکسل
در اکسل، از دو تابع STDEV.S(number1,[number2],…) و STDEVA(value1, [value2], …) برای محاسبه انحراف معیار تعدادی نمونه از جمعیت کل استفاده میشود. برای محاسبه انحراف معیار جمعیت در اکسل میتوانیم از توابع STDEVP ، STDEV.P و STDEVPA استفاده کنیم.
- تابع STDEVP در اکسل: تابع STDEVP(number1,[number2],…) تابعی قدیمی در اکسل برای محاسبه انحراف معیار جمعیت است، اما در نسخههای اکسل ۲۰۱۰، ۲۰۱۳، ۲۰۱۶ و ۲۰۱۹ از تابعSTDEV.P به جای تابع STDEVP برای محاسبه انحراف معیار جمعیت استفاده میشود.
- تابع STDEV.P در اکسل: تابع STDEV.P(number1,[number2],…) بهبود یافته تابع STDEVP(number1,[number2],…) و انحراف معیار را با دقت نسبتا بالایی محاسبه میکند.
- تابع STDEVPA در اکسل: این تابع انحراف معیار جمعیت شامل متغیرهای متنی و منطقی را محاسبه میکند.
از کدام تابع انحراف معیار در اکسل استفاده کنیم؟
انتخاب تابع مناسب از میان شش تابع برای محاسبه انحراف معیار در اکسل، ممکن است برای کاربرهای تازهکار و بیتجربه، سخت و وقتگیر باشد. برای انتخاب تابع مناسب برای محاسبه انحراف معیار، تنها کافی است به سه پرسش زیر پاسخ دهید:
- چه انحراف معیاری را محاسبه میکنید؟ انحراف معیار جمعیت یا انحراف معیار نمونه؟
- از کدام نسخه اکسل استفاده میکنید؟
- آیا دادههای شما تنها اعداد هستند یا متغیرهای منطقی و متنی را نیز در بر میگیرند؟
همچنین، به این نکته توجه داشته باشید که:
- برای محاسبه انحراف معیار مجموعهای انتخاب شده از جمعیت کل، از تابع STDEV.S در اکسل ۲۰۱۰ و بعد از آن و از تابع STDEV در اکسل ۲۰۰۷ و قبل از آن استفاده کنید.
- برای محاسبه انحراف معیار جمعیت کل، از تابع STDEV.P در اکسل ۲۰۱۰ و بعد از آن و از تابع STDEVP در اکسل ۲۰۰۷ و قبل از آن استفاده کنید.
- اگر دادهها متنی یا منطقی هستند، از تابع STDEVA برای محاسبه انحراف معیار نمونه و از تابع STDEVPA برای محاسبه انحراف معیار جمعیت استفاده کنید.
مثال محاسبه انحراف معیار در اکسل
تا اینجا فهمیدیم انحراف معیار چیست و با چه فرمولهایی محاسبه میشود. در این قسمت با استفاده از چند مثال، انحراف معیار جمعیت و نمونهای انتخاب شده از جمعیت را در اکسل بهدست میآوریم. پس از انتخاب تابع مناسب برای دادههای خود، به راحتی میتوانید انحراف معیار را در اکسل محاسبه کنید. فرض کنید نمرههای درس ریاضی ۵۲ دانشآموز در اکسل نوشته شده است:
- اگر بخواهیم انحراف معیار نمرههای ریاضی تمام ۵۲ دانشآموز را بهدست آوریم، از تابع =STDEV.P(B2:B51) استفاده میکنیم. زیرا تمام جمعیت دانشآموزان انتخاب شده است.
- اگر بخواهیم انحراف معیار نمرههای ریاضی تمام ۱۴ دانشآموز را بهدست آوریم، از تابع =STDEV.P(B2:B51) استفاده میکنیم. زیرا از بین ۵۲ دانشآموز، ۱۵ دانشآموز انتخاب شدهاند.
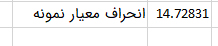
ابتدا انحراف معیار ۵۲ دانشآموز را بهدست میآوریم. همانطور که در تصویر زیر مشاهده میکنید، انحراف معیار جمعیت برابر ۱۳/۸۸ به دست آمده است.

در ادامه، انحراف معیار ۱۴ دانشآموز را بهدست میآوریم. همانطور که در تصویر زیر مشاهده میکنید، انحراف معیار نمونه برابر ۱۴/۷۳ به دست آمده است.
محاسبه انحراف معیار برای نمایش متنی اعداد
در مطالب بالا و به هنگام معرفی توابع مورد استفاده برای محاسبه انحراف معیار در اکسل از عبارت «نمایش متنی اعداد» استفاده کردیم. این عبارت چه معنایی دارد؟ به زبان ساده، این عبارت به معنای نوشتن اعداد در قالب متن است. این اعداد چگونه در اکسل نمایش داده میشوند؟ در بیشتر موارد اعداد به صورت فایلهایی به اکسل منتقل و در آن به صورت متن نمایش داده میشوند. برای درک بهتر چگونگی کار با اعداد متنی، مثالی را در ادامه با یکدیگر بررسی میکنیم. فرض کنید ستونی در اکسل دارید که از محصولی مشخص به همراه کد آن محصول مانند «Jeans-105» تشکیل شده است. هدف شما آن است که کد هر محصول را بردارید و انحراف معیار آنها را محاسبه کنید.
قرار دادن کد محصولات در ستونِ دیگر، مشکلی ندارد. با استفاده از دستور =RIGHT(A2,LEN(A2)-SEARCH("-",A2,1)) به راحتی میتوانید این کار را انجام دهید.
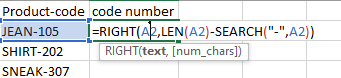
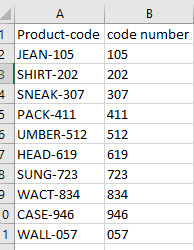
با اجرای این دستور برای تمام محصولات، به راحتی میتوانیم کد آنها را استخراج و در ستونی جداگانه بنویسیم.
در ادامه، میخواهیم انحراف معیار کدهای استخراج شده را محاسبه کنیم. نتیجه عجیبی نشان داده میشود.

دلیل این اتفاق چیست؟ به هنگام استفاده از تابع RIGHT به این نکته باید توجه داشته باشیم که خروجی این تابع همواره رشته متنی است. اما توابع STDEV.S و STDEVA نمیتوانند با اعدادی به شکل متن، کار کنند. همچنین، STDEVA اعداد متنی را صفر در نظر میگیرد. چه کاری میتوان انجام داد؟ برای محاسبه انحراف معیارِ اعداد متنی باید آنها را به طور مستقیم در لیست آرگومانها قرار دهید. این کار را میتوان با قرار دادن تابع RIGHT در فرمول STDEV.S به صورت زیر انجام داد:
=STDEV.S(RIGHT(A2,LEN(A2)-SEARCH("-",A2,1)), RIGHT(A3,LEN(A3)-SEARCH("-",A3,1)), RIGHT(A4,LEN(A4)-SEARCH("-",A4,1)), RIGHT(A5,LEN(A5)-SEARCH("-",A5,1)), RIGHT(A6,LEN(A5)-SEARCH("-",A6,1)), RIGHT(A7,LEN(A5)-SEARCH("-",A7,1)), RIGHT(A5,LEN(A8)-SEARCH("-",A8,1)), RIGHT(A5,LEN(A9)-SEARCH("-",A9,1)), RIGHT(A5,LEN(A10)-SEARCH("-",A10,1)), RIGHT(A5,LEN(A11)-SEARCH("-",A11,1)))
همچنین، تابع RIGHT را میتوانیم به صورت زیر در فرمول STDEVA قرار دهیم:
=STDEVA(RIGHT(A2,LEN(A2)-SEARCH("-",A2,1)), RIGHT(A3,LEN(A3)-SEARCH("-",A3,1)), RIGHT(A4,LEN(A4)-SEARCH("-",A4,1)), RIGHT(A5,LEN(A5)-SEARCH("-",A5,1)), RIGHT(A6,LEN(A5)-SEARCH("-",A6,1)), RIGHT(A7,LEN(A5)-SEARCH("-",A7,1)), RIGHT(A5,LEN(A8)-SEARCH("-",A8,1)), RIGHT(A5,LEN(A9)-SEARCH("-",A9,1)), RIGHT(A5,LEN(A10)-SEARCH("-",A10,1)), RIGHT(A5,LEN(A11)-SEARCH("-",A11,1)))
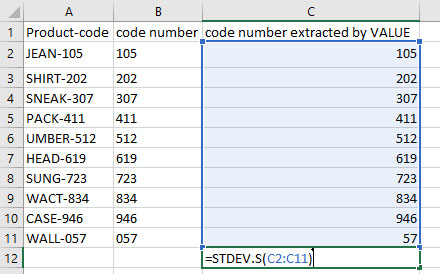
فرمولهای بالا کمی طولانی هستند، اما با استفاده از آنها میتوانیم انحراف معیار اعداد متنی را بهدست آوریم. سوالی که ممکن است مطرح شود آن است که اگر تعداد اعداد متنی بسیار بیشتر بودند چه کاری میتوان انجام داد. در این حالت، میتوان با استفاده از تابع VALUE اعداد متنی را به اعداد تبدیل کنیم و در ادامه، انحراف معیار آنها را به راحتی محاسبه کنیم. از تابع VALUE به صورت نشان داده شده در تصویر زیر استفاده میکنیم.

همانطور که در تصویر زیر مشاهده میکنیم با نوشتن این دستور در ستون C و اعمال آن برای سطرهای A2 تا A11، بارکد محصولات به صورت عددی خارج میشوند. در ادامه، به راحتی میتوانیم انحراف معیار اعداد استخراج شده را بهدست آوریم.
چگونه نوارهای انحراف معیار را در اکسل اضافه کنیم؟
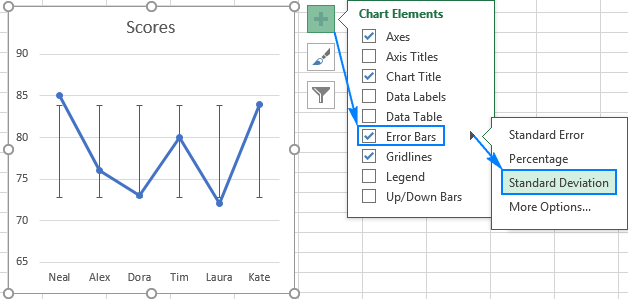
در این بخش، چگونگی اضافه کردن نوارهای انحراف معیار به نمودارهای رسم شده را توضیح میدهیم:
- نمودار خود را با رفتن به قسمت Insert و انتخاب Charts group رسم کنید.
- در هر قسمت دلخواهی روی نمودار کلیک و با انتخاب آن، دکمه Chart Elements را انتخاب کنید.
- روی مثلث کوچک در کنار Error Bars کلیک و Standard Deviation را انتخاب کنید.
با دنبال کردن مراحل فوق، نوارهای مشابهی برای تمام دادهها رسم میشوند. مراحل فوق، در تصویر زیر نشان داده شده است.
انحراف معیار و خطای استاندارد میانگین
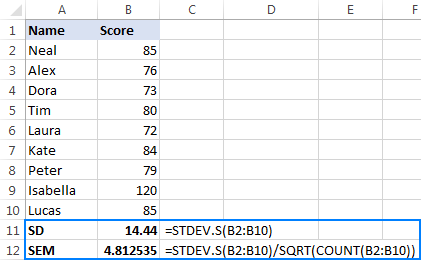
در آمار، اندازهگیری و معیار دیگری برای تخمین تنوعِ دادهها به نام «خطای استاندارد میانگین» (Standard Error of the Mean | SEM) وجود دارد. انحراف معیار و خطای استاندارد میانگین دو مفهوم بسیار نزدیک به یکدیگر هستند، اما یکسان نیستند. انحراف معیار، پراکندگی و انحراف دادههای از مقدار میانگین را اندازهگیری میکند، اما خطای استاندارد میانگین به ما میگوید میانگین نمونه انتخاب شده از جمعیت کل چه مقدار از میانگین واقعی جمعیت کل فاصله دارد. انحراف معیار همواره از خطای استاندارد میانگین بزرگتر است. خطای استاندارد میانگین از نسبت انحراف معیار بر جذر اندازه نمونه بهدست میآید.
خطای استاندارد میانگین در اکسل را میتوانیم به کمک توابع STDEV.S و COUNT و SQRT با استفاده از فرمول زیر بهدست آوریم:
STDEV.S(range)/SQRT(COUNT(range))
اگر دادههای نمونه در ستونهای B2 تا B10 نوشته شده باشند، فرمول SEM به صورت زیر نوشته میشود:
=STDEV.S(B2:B10)/SQRT(COUNT(B2:B10))
چگونگی استفاده از این فرمول در تصویر زیر نشان داده شده است.
محاسبه انحراف معیار در پایتون
تا اینجا میدانیم انحراف معیار چیست، چه تفاوتی با واریانس دارد و چگونه میتوانیم آن را با استفاده از اکسل محاسبه کنیم. در این قسمت، مقدارهای واریانس و انحراف معیار را با استفاده از برنامه پایتون بهدست میآوریم.
برای انجام این کار باید از کتابخانه Statistics و برای رسم انحراف معیار از کتابخانه pyplot استفاده میکنیم. فراخوانی این کتابخانهها در برنامه پایتون به صورت زیر انجام میشود:
1import statistics as st
2import matplotlib.byplot as ppمجموعه دادهها را در متغیری به نام و به شکل «تاپل» (Tuple) ذخیره میکنیم. فرض میکنیم مقدارهای داده شده برای محاسبه انحراف معیار و واریانس، تمام دادهها و نه مجموعهای انتخاب شده از دادهها، هستند. در نتیجه، از توابع انحراف معیار و واریانس جمعیت استفاده میکنیم. پس از فراخوانی کتابخانههای لازم، دادهها را به شکل تاپل و به صورت زیر مینویسیم:
1import statistics as st
2import matplotlib.byplot as pp
3x = [4.2,4.3,4.1,3.9,4.5,3.6,3.7,3.8,4.0]تابع st.pstdev() انحراف معیار دادهها را محاسبه و ذخیره میکند. همچنین، با استفاده از تابع st.pvariance() واریانس دادهها را محاسبه میکنیم.
1import statistics as st
2import matplotlib.byplot as pp
3x = [4.2,4.3,4.1,3.9,4.5,3.6,3.7,3.8,4.0]
4sd = st.pstdev(x)
5v = st.pvariance(x)همچنین، برای تحلیل و رسم دادهها به مقدار میانگین نیز نیاز داریم. برای محاسبه مقدار میانگینِ مجموعهای از دادهها در پایتون، از تابع st.mean() استفاده میکنیم.
1import statistics as st
2import matplotlib.byplot as pp
3x = [4.2,4.3,4.1,3.9,4.5,3.6,3.7,3.8,4.0]
4sd = st.pstdev(x)
5v = st.pvariance(x)
6m = st.mean(x)با نوشتن مقدارهای انحراف معیار، واریانس و میانگین از تابع print() به صورت زیر استفاده میکنیم.
1import statistics as st
2import matplotlib.byplot as pp
3x = [4.2,4.3,4.1,3.9,4.5,3.6,3.7,3.8,4.0]
4sd = st.pstdev(x)
5v = st.pvariance(x)
6m = st.mean(x)
7print("Standard deviation: " +str(sd))
8print("Variance: " +str(v))
9print("Mean: " +str(m))در ادامه برنامه و پس از محاسبه انحراف معیار، واریانس و مقدار میانگین، نمودارهای لازم را رسم میکنیم. برای انجام این کار ابتدا مقدارهای محاسبه شده را ذخیره میکنیم. ادامه برنامه به صورت زیر نوشته میشود:
1import statistics as st
2import matplotlib.byplot as pp
3x = [4.2,4.3,4.1,3.9,4.5,3.6,3.7,3.8,4.0]
4sd = st.pstdev(x)
5v = st.pvariance(x)
6m = st.mean(x)
7print("Standard deviation: " +str(sd))
8print("Variance: " +str(v))
9print("Mean: " +str(m))
10sdx = tuple(x-m for x in x)
11print("Standard Deviations: " + str (sdx))
12varx = tuple(x*x for x in sdx)
13print("Variances: "+ str(varx))
14pp.bar(tuple(str(x) for x in x), sdx)خروجی برنامه فوق از دو قسمت محاسبه و نمودار تشکیل شده است. خروجی قسمت محاسبات به صورت زیر است:
Standard deviation: 0.2766644355108607 Variance: 0.07654320987654319 Mean: 4.011111111111111 Standard Deviations: (0.1888888888888891, 0.28888888888888875, 0.08888888888888857, -0.11111111111111116, 0.48888888888888893, -0.411111111111111, -0.3111111111111109, -0.21111111111111125, -0.011111111111111072) Variances: (0.03567901234567909, 0.0834567901234567, 0.00790123456790118, 0.01234567901234569, 0.2390123456790124, 0.16901234567901224, 0.09679012345678999, 0.04456790123456796, 0.00012345679012345593)
محاسبه آنلاین انحراف معیار
با جستجوی عبارت «how to calculate standard deviation online» در گوگل میتوانید سایتهای زیادی را پیدا کنید که انحراف معیار را به صورت آنلاین محاسبه میکنند. به عنوان مثال، با ورود به سایت Calculator.net «+» و ورود دادههای خود به راحتی میتوانید انحراف معیار نمونه یا جمعیت را محاسبه کنید.
محاسبه انحراف معیار در SPSS
پس از آنکه فهمیدیم انحراف معیار چیست و چگونه در اکسل، پایتون و به صورت آنلاین محاسبه میشود، در این بخش چگونگی محاسبه آن را در SPSS به صورت خلاصه توضیح میدهیم.
فرض کنید تعدادی داده دارید که میخواهید انحراف معیار آنها را در نرمافزار SPSS بهدست آورید. دادهها را ابتدا به صورت نشان داده شده در تصویر زیر به SPSS میدهیم.
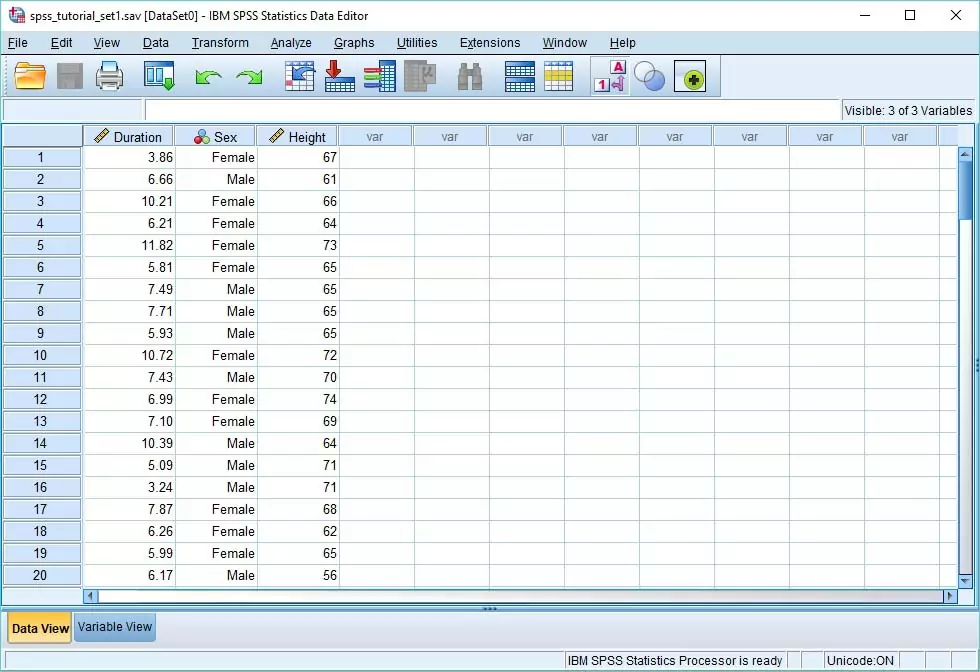
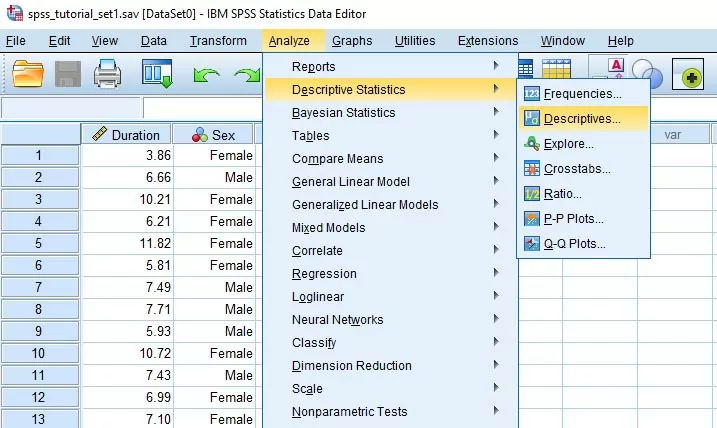
همانطور که در تصویر زیر مشاهده میکنید، دادههای از سه قسمت تشکیل شدهاند. با توجه به دادههای اندازهگیری شده، متوسط زمان انجام کار یا پراکندگی زمان را میخواهیم. برای محاسبه میانگین و انحراف معیار، مسیر نشان داده شده در تصویر زیر را طی میکنیم.
با دنبال کردن مسیر نشان داده شده در تصویر فوق، جعبه زیر باز میشود.
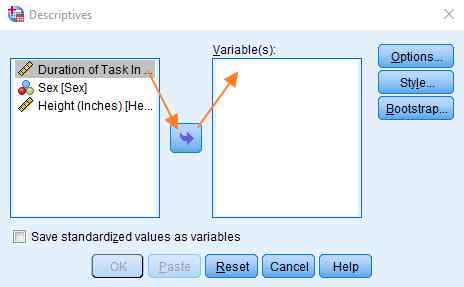
متغیری که میخواهیم میانگین و انحراف معیار آن را بهدست آوریم به قسمت Variable منتقل میکنیم. برای انجام این کار، متغیر موردنظر را در سمت چپ انتخاب میکنیم. در ادامه، با کلیلک روی فلش آبیرنگ، متغیر به قسمت Variable منتقل میشود. پس از انتخاب متغیر موردنظر، روی گزینه Options کلیک و میانگین و انحراف معیار را انتخاب میکنیم.
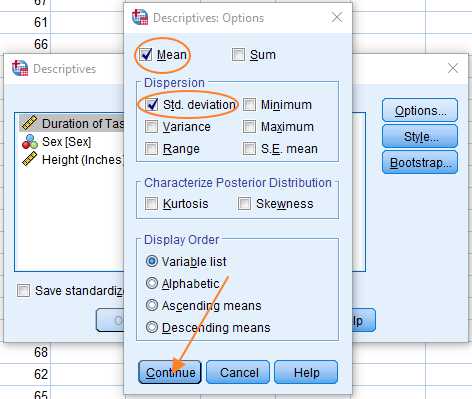
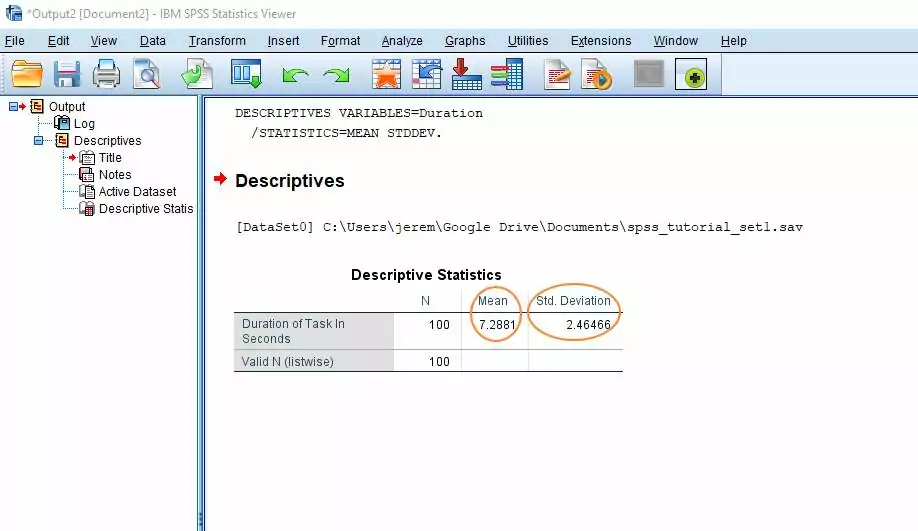
در ادامه، با کلیک روی Continue و سپس کلیک روی Ok، نتیجه بهدست میآید. نتایج در SPSS به صورت زیر نشان داده میشوند.
جمعبندی
در این مطلب از مجله فرادرس فهمیدیم انحراف معیار چیست. انحراف به ما میزان پراکندگی دادههای آماری جمعآوری شده را نشان میدهد. به بیان دیگر، انحراف معیار اطلاعاتی در مورد میزان تغییر مقدار دادههای آماری به ما میدهد. هرچه مقدار انحراف بزرگتر باشد، میزان پراکندگی و تغییر دادههای آماری نیز بیشتر خواهد بود. پس از خواندن این مطلب فهمیدیم:
- انحراف معیار چیست و با چه روشهایی محاسبه میشود.
- تفاوت واریانس و انحراف معیار چیست.
- چگونه انحراف معیار را در اکسل و پایتون محاسبه کنیم.













با سلام و خسته نباشید خدمت عوامل محترم فرادرس…
احساس میکنم اشتباهی در بخش: تفاوت واریانس و انحراف معیار وجود داره…قسمت اول واریانس چیست…
از لحاظ تعریف ریاضی به اشتباه نوشته شده جذر انحراف معیار میشه واریانس…فقط جذر باید به توان 2 تبدیل بشه…
با سلام و وقت بخیر؛
فرمول اصلاح شد.
از همراهی شما با مجله فرادرس سپاسگزاریم.