پیش‌تر در بلاگ فرادرس نحوه محاسبه انتگرال خطی روی میدان اسکالر را توضیح دادیم. در این بخش قصد داریم تا نحوه محاسبه انتگرال خطیِ توابع برداری را توضیح دهیم.
فرمول انتگرال خطی
به منظور محاسبه انتگرال، در ابتدا تابعی برداری را مطابق با رابطه زیر در نظر بگیرید.
$$ \large \overrightarrow F \left ( { x , y , z } \right ) = P \left ( { x , y , z } \right ) \overrightarrow i + Q \left ( { x , y , z } \right ) \overrightarrow j + R \left ( { x , y , z } \right ) \overrightarrow k$$
هم‌چنین خم C را در قالب تابعی پارامتری به شکل زیر در نظر بگیرید.
$$\large \overrightarrow r \left ( t \right ) = x \left ( t \right ) \overrightarrow i + y \left ( t \right ) \overrightarrow j + z \left ( t \right ) \overrightarrow k\hspace {0.25in} \hspace {0.25in} a \le t \le b $$
در این صورت حاصل انتگرال خطی تابع $$ \overrightarrow {F} $$ روی خم C برابر است با:
$$\large \int \limits _ { C } { { \overrightarrow F \small \bullet d \, \overrightarrow r } } = \int _ { { \, a } } ^ { { \, b } } { { \overrightarrow F \left ( { \overrightarrow r \left ( t \right ) } \right ) \small \bullet \overrightarrow r ^{\prime} \left ( t \right ) \, d t } } $$
توجه داشته باشید که عبارت زیرِ انتگرال در سمت چپ، حاصل ضرب داخلی دو بردار محسوب می‌شود. هم‌چنین تابع $$ \overrightarrow {F} $$ به صورت زیر است.
$$ \large \overrightarrow F \left ( { \overrightarrow r \left ( t \right ) } \right ) = \overrightarrow F \left ( { x \left ( t \right ) , y \left ( t \right ) , z \left ( t \right ) } \right ) $$
البته حاصل انتگرالِ تابع برداری را می‌توان بر حسب طول خم به صورت زیر نیز بیان کرد:
$$\large \int \limits _ { C } { { \overrightarrow F \small \bullet d \, \overrightarrow r } } = \int \limits _ { C } { { \overrightarrow F \small \bullet \overrightarrow T \, d s } } $$
توجه داشته باشید که T بردار مماس بر خم را در هر نقطه از آن نشان می‌دهد. این بردار مطابق با رابطه زیر بدست می‌آید.
$$\large \overrightarrow T \left ( t \right ) = \frac { { \overrightarrow r ^{\prime} \left ( t \right ) } } { { \left \| { \overrightarrow r ^{\prime} \left ( t \right ) } \right \| } } $$
با استفاده از رابطه فوق، حاصل انتگرال تابع برداری F روی خم C برابر می‌شود با:
$$ \large \begin {align*} \int \limits _ { C } { { \overrightarrow F \small \bullet d \, \overrightarrow r } } & = \int \limits _ { C }{ { \overrightarrow F \small \bullet \overrightarrow T \, d s } } \\ & = \int _ { { \, a } } ^ { { \, b } } { { \overrightarrow F \left ( { \overrightarrow r \left ( t \right ) } \right ) \small \bullet \frac { { \overrightarrow r ^{\prime} \left ( t \right ) } } { { \left \| { \overrightarrow r ^{\prime} \left ( t \right ) } \right \| } } \, \, \left \| { \overrightarrow r ^{\prime} \left ( t \right ) } \right \| \, d t } } \\ & = \int _ { { \, a } } ^ { { \, b } } { { \overrightarrow F \left ( { \overrightarrow r \left ( t \right ) } \right ) \small \bullet \overrightarrow r ^{\prime} \left ( t \right ) \, d t } } \end {align*} $$
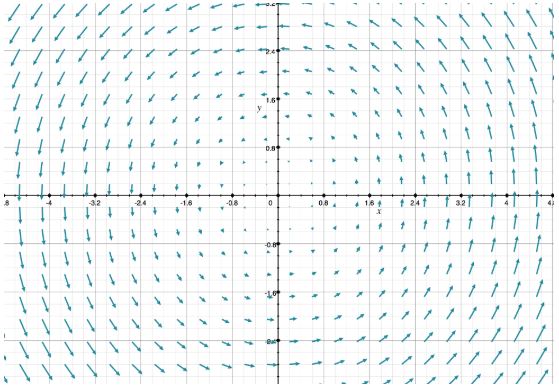
توجه داشته باشید که میدان یا تابع برداری به رابطه‌ای اشاره دارد که در هر نقطه از یک ناحیه دارای اندازه و جهت است. برای نمونه شکل زیر می‌تواند بیان‌گر میدان سرعت آب در یک ناحیه باشد.
در ادامه مثال‌هایی ارائه شده که پیشنهاد می‌شود آن‌ها را مطالعه فرمایید.
مثال ۱
حاصل انتگرالِ خطی تابع F یا همان $$\int \limits _ { C } { { \overrightarrow F \small \bullet d \overrightarrow r}}$$ را روی خم C بدست آورید. فرض کنید تابع F و رابطه توصیف کننده خم C به ترتیب برابر با $$ \overrightarrow F \left ( { x , y , z } \right ) = 8 { x ^ 2 } y \, z \, \overrightarrow i + 5 z \, \overrightarrow j – 4 x \, y \, \overrightarrow k $$ و $$ \overrightarrow r \left ( t \right ) = t \, \overrightarrow i + { t ^ 2 } \, \overrightarrow j + { t ^ 3 } \, \overrightarrow k $$ باشند. هم‌چنین t در بازه $$ 0 \le t \le 1 $$ قرار دارد.
به منظور محاسبه انتگرال در اولین قدم بایستی تابع برداری F بر حسب t بیان شود. بنابراین داریم:
$$\large \overrightarrow F \left ( { \overrightarrow r \left ( t \right ) } \right ) = 8 { t ^ 2 } \left ( { { t ^ 2 } } \right ) \left ( { { t ^ 3 } } \right ) \overrightarrow i + 5 { t ^ 3 } \, \overrightarrow j – 4 t \left ( { { t ^ 2 } } \right ) \overrightarrow k = 8 { t ^ 7 } \, \overrightarrow i + 5 { t ^ 3 } \, \overrightarrow j – 4 { t ^ 3 } \, \overrightarrow k $$
در قدم بعدی مشتق تابع برداری r را به صورت زیر بدست می‌آوریم.
$$ \large \overrightarrow r ^{\prime} \left ( t \right ) = \, \overrightarrow i + 2 t \, \overrightarrow j + 3 { t ^ 2 } \, \overrightarrow k $$
در مرحله بعد حاصل ضرب داخلی دو برابر F و $$ r ^ {\prime} $$ برابر می‌شود با:
$$ \large \overrightarrow F \left ( { \overrightarrow r \left ( t \right ) } \right ) \small \bullet \overrightarrow r ^{\prime} \left ( t \right ) = 8 { t ^ 7 } + 1 0 { t ^ 4 } – 1 2 { t ^ 5 } $$
نهایتا حاصل انتگرال خطی برابر می‌شود با:
$$ \large \begin {align*} \int \limits _ { C } { { \overrightarrow F \small \bullet d \, \overrightarrow r } } & = \int _ { { \, 0 } } ^ { { \, 1 } } { { 8 { t ^ 7 } + 1 0 { t ^ 4 } – 1 2 { t ^ 5 } \, d t } } \\ & = \left. { \left ( { { t ^ 8 } + 2 { t ^ 5 } – 2 { t ^ 6 } } \right ) } \right|_0 ^ 1 \\ & = 1 \end {align*} $$
مثال ۲
حاصل انتگرالِ خطیِ $$ \int \limits _ { C } { { \overrightarrow F \small \bullet d \, \overrightarrow r } } $$ را در حالتی محاسبه کنید که تابع F برابر با $$ \overrightarrow F \left ( { x , y , z } \right ) = x \, z \, \overrightarrow i – y \, z \, \overrightarrow k $$ بوده و خم C برابر با خطی از نقطه $$ \left ( { – 1 , 2 , 0 } \right ) $$ به نقطه $$ \left ( { 3 , 0 , 1 } \right ) $$ در نظر گرفته شده است.
با توجه به نقاط ابتدایی و انتهایی خط، شکل پارامتری r را می‌توان به صورت زیر بیان کرد:
$$ \large \begin {align*} \overrightarrow r \left ( t \right ) & = \left ( { 1 – t } \right ) \left \langle { – 1 , 2 , 0 } \right \rangle + t \left \langle { 3 , 0 , 1 } \right \rangle \\ & = \left \langle { 4 t – 1 , 2 – 2 t , t } \right \rangle ,\hspace {1.0in} 0 \le t \le 1 \end {align*} $$
بنابراین مشتق بردار r نیز به صورت زیر بدست می‌آید.
$$ \large \overrightarrow r ^{\prime} \left( t \right) = \left \langle { 4 , – 2 , 1 } \right \rangle $$
با داشتن F و محاسبه مشتق r، حاصل‌ضرب داخلی این دو بردار را می‌توان به صورت زیر بدست آورد.
$$ \large \overrightarrow F \left ( { \overrightarrow r \left ( t \right ) } \right ) \small \bullet \overrightarrow r ^{\prime} \left ( t \right ) = 4 \left ( { 4 { t ^ 2 } – t } \right ) – \left ( { 2 t – 2 { t ^ 2 } } \right ) = 1 8 { t ^ 2 } – 6 t $$
در نتیجه حاصل انتگرال خطی روی این میدان نیز به صورتی که در ادامه آمده، بدست خواهد آمد.
$$ \large \begin {align*} \int \limits _ { C } { { \overrightarrow F \small \bullet d \, \overrightarrow r } } & = \int _ { {\, 0 } } ^ { { \, 1 } } { { 1 8 { t ^ 2 } – 6 t \, d t } } \\ & = \left. { \left ( { 6 { t ^ 3 } – 3 { t ^ 2 } } \right)} \right|_0^1\\ & = 3 \end {align*} $$
این مطلب را با بدست آوردن رابطه‌ای کوتاه‌تر به منظور محاسبه انتگرال خطی روی تابع برداری به پایان می‌بریم. به این منظور در ابتدا تابع برداری F را به صورت $$ \overrightarrow F \left ( { x , y , z } \right ) = P \, \overrightarrow i + Q \, \overrightarrow j + R \, \overrightarrow k $$ در نظر بگیرید. هم‌چنین فرض کنید خم C با استفاده از تابعی پارامتری مطابق با رابطه $$ \overrightarrow r \left ( t \right ) = x \left ( t \right ) \overrightarrow i + y \left ( t \right ) \overrightarrow j + z \left ( t \right ) \overrightarrow k $$ در بازه $$ a \le t \le b $$ توصیف می‌شود. در این صورت حاصل انتگرالِ خطی تابع F روی خم C برابر است با:
$$ \large \begin {align*} \int \limits _ { C } { { \overrightarrow F \small \bullet d \, \overrightarrow r } } & = \int _ { { \, a } } ^ { { \, b } } { { \left ( { P \, \overrightarrow i + Q \, \overrightarrow j + R \, \overrightarrow k } \right ) \small \bullet \left ( { x ^{\prime} \, \overrightarrow i + y ^{\prime} \, \overrightarrow j + z ^{\prime} \, \overrightarrow k } \right ) \, d t } } \\ & = \int _ { { \, a } } ^ { { \, b } } { { P x ^{\prime} + Q y ^{\prime} + R z ^{\prime} \, d t } } \\ & = \int _ { { \, a } } ^ { { \, b } } { { P x ^{\prime}\, d t } } + \int _ { { \, a } } ^ { { \, b } } { { Q y ^{\prime}\ , d t } } + \int _ { { \, a } } ^ { { \, b } } { { R z ^{\prime} \, d t } } \\ & = \int \limits _ { C } { { P \, d x } } + \int \limits _ { C } { { Q \, d y } } + \int \limits _ { C } { { R \, d z } } \\ & = \int \limits _ { C } { { P \, d x } } + Q \, d y + R \, d z \end {align*} $$
در نتیجه می‌توان رابطه کلی زیر را برای انتگرال خطی یک تابع ارائه داد.
$$\large \boxed {\int \limits _ { C } { { \overrightarrow F \small \bullet d \, \overrightarrow r } } = \int \limits _ { C } { { P \, d x } } + Q \, d y + R \, d z} $$
بنابراین رابطه فوق روشی متفاوت را برای بدست آوردن انتگرال خطی بیان می‌کند. البته رابطه مذکور این مفهوم را نیز بیان می‌کند که انتگرال روی دو مسیری که عکس هم باشند، قرینه یکدیگر هستند. بنابراین رابطه زیر را می‌توان برای انتگرالِ روی مسیری عکس بیان کرد.
$$\large \int \limits _ { { – C } } { { \overrightarrow F \small \bullet d \, \overrightarrow r } } = – \int \limits _ { C } { { \overrightarrow F \small \bullet d \, \overrightarrow r } } $$
مثال ۳
حاصل انتگرالِ $$ \int \limits _ { C } { { \overrightarrow F \small \bullet d \, \overrightarrow r } } $$ را روی مسیر C بیابید. فرض کنید تابع برداریِ F برابر با $$ \overrightarrow F \left ( { x , y } \right ) = { y ^ 2 } \, \overrightarrow i + \left ( { { x ^ 2 } – 4 } \right ) \overrightarrow j $$ بوده و مسیر انتگرال‌گیری، تابع $$ y = { \left ( { x – 1 } \right ) ^ 2 } $$ از نقطه x=0 تا x=3 است.
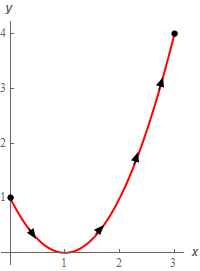
در این مثال، مسیر C به صورت پارامتری بیان نشده. بنابراین لازم است ابتدا تصویری از مسیر انتگرال‌گیری را در ذهن خود داشته باشید. در ادامه مسیر انتگرال‌گیری ترسیم شده است.
اگر x=t در نظر گرفته شود، $$ y = ( t – 1 ) ^2 $$ شده و شکل پارامتری خم بالا، به صورت زیر بدست می‌آید.
$$\large \overrightarrow r \left ( t \right ) = \left \langle { t , { { \left ( { t – 1 } \right ) } ^ 2 } } \right \rangle \, \, \, \, \, \, \, \, 0 \le t \le 3 $$
به منظور محاسبه انتگرال تابع، در ابتدا بایستی حاصل‌ضرب داخلی دو بردار F و $$ r ^ {\prime} $$ را بدست آوریم. بدین منظور توابع F و $$ r ^ {\prime} $$ برابر با عبارت‌های زیر بدست می‌آیند.
$$ \large \overrightarrow F \left ( { \overrightarrow r \left ( t \right ) } \right ) = { \left [ { { { \left ( { t – 1 } \right ) } ^ 2 } } \right ] ^ 2 } \, \overrightarrow i + \left ( { { { \left ( t \right ) } ^ 2 } – 4 } \right ) \overrightarrow j = { \left ( { t – 1 } \right ) ^ 4 } \, \overrightarrow i + \left ( { { t ^ 2 } – 4 } \right ) \overrightarrow j $$
هم‌چنین $$ r ^ {\prime} $$ برابر است با:
$$ \large \overrightarrow r ^{\prime} \left ( t \right ) = \left \langle { 1 , 2 \left ( { t – 1 } \right ) } \right \rangle $$
بنابراین حاصل‌ضرب داخلی دو بردارِ فوق برابر است با:
$$ \large \begin {align*} \overrightarrow F \left ( { \overrightarrow r \left ( t \right ) } \right ) \small \bullet \overrightarrow r ^{\prime} \left ( t \right ) & = { \left ( { t – 1 } \right ) ^ 4 } \left ( 1 \right ) + \left ( { { t ^ 2 } – 4 } \right ) \left ( { 2 t – 2 } \right )\\ & = { \left ( { t – 1 } \right ) ^ 4 } + 2 { t ^ 3 } – 2 { t ^ 2 } – 8 t + 8 \end {align*} $$
حال می‌توان انتگرال را به راحتی و به شکلی که در ادامه آمده، محاسبه کرد.
$$ \large \begin {align*} \int \limits _ { C } { { \overrightarrow F \small \bullet d \overrightarrow r } } & = \int _ { 0 } ^ { 3 }{ { { { \left ( { t – 1 } \right ) } ^ 4 } + 2 { t ^ 3 } – 2 { t ^ 2 } – 8 t + 8 \, d t } } \\ & = \left. { \left [ { \frac { 1 }{ 5 } { { \left ( { t – 1 } \right ) } ^ 5 } + \frac { 1 } { 2 } { t ^ 4 } – \frac { 2 } { 3 } { t ^ 3 } – 4 { t ^ 2 } + 8 t } \right]} \right|_ 0 ^ 3 = { { \frac { { 1 7 1 } }{ { 1 0 } } } } \end {align*} $$
در صورت علاقه‌مندی به مباحث مرتبط در زمینه ریاضی، آموزش‌های زیر نیز به شما پیشنهاد می‌شوند:
- مجموعه آموزش‌های دروس ریاضی
- مجموعه آموزش‌های ریاضی و فیزیک
- مفاهیم، روش های محاسبه و کاربردهای انتگرال — مجموعه مقالات وبلاگ فرادرس
- انتگرال خطی — به زبان ساده
- تابع برداری — به زبان ساده
^^
ممنون خیلی خوب توضیح داده شده است
عالی بود
سپاسگزارم
دستتون درد نکنه خیلی خوب بود
هر گونه بهرهگیری از مطالب مجله فرادرس به معنی پذیرش شرایط استفاده از آن بوده و کپی بخش یا کل هر کدام از مطالب، تنها با کسب مجوز مکتوب امکان پذیر است.
© فرادرس ۱۴۰۱
ورود / ثبتنام