اصطلاحات یادگیری عمیق — راهنمای کاربردی

در این مطلب، مهمترین اصطلاحات یادگیری عمیق مورد بررسی قرار گرفتهاند. این روزها، هوش مصنوعی دارد دنیای ما را تسخیر میکند. «یادگیری ماشین» و «یادگیری عمیق» بخش بزرگی از زندگی انسانها را تشکیل میدهند. (مارک کوبان) در این مورد میگوید:
«هوش مصنوعی، یادگیری عمیق و یادگیری ماشین». مهم نیست کارتان چیست، اگر این موضوعات را درک نمیکنید، آنها را یاد بگیرید. در غیر این صورت تا 3 سال دیگر منقرض خواهید شد.
شاید این جملهی مارک کوبان به نظر بیش از حد سنگین بیاید، ولی کاملا درست است! ما در دوران یک انقلاب زندگی میکنیم، انقلابی که توسط کلان دادهها و قدرتهای محاسباتی زیاد ایجاد شده است. یک دقیقه با خودتان فکر کنید که اگر فردی در قرن بیستم چیزی راجع به برق نداند چه حسی دارد. سالها عادت کرده بودید که کارها را به طور خاصی انجام دهید و حالا یک دفعه همه چیز شروع به تغییر میکند. کارهایی که برای انجام نیازمند افراد زیادی بود، حالا با وجود برق میتواند توسط یک نفر انجام شود. امروزه با یادگیری ماشین (Machine Learning) و یادگیری عمیق (Deep Learning)، ماجرای مشابهی را تجربه خواهیم کرد.
پس اگر هنوز هم قدرت یادگیری عمیق را درک نکردهاید، باید از همین امروز شروع به یادگیری کنید. این مقاله به شما کمک میکند که مفاهیم پایه و بیشتر استفاده شدهی یادگیری عمیق را یاد بگیرید.
این مقاله برای چه کسانی مناسب است؟
اگر علاقهمند به یادگیری و درک «یادگیری عمیق» هستید، این مقاله برای شما نوشته شده است. در این مقاله به توضیح اصطلاحات متفاوتی که در یادگیری عمیق استفاده میشوند، میپردازیم. درک یادگیری عمیق میتواند کمی سخت و طاقتفرسا باشد. این مقاله با این هدف نوشته شده است که یادگیری و درک «یادگیری عمیق» را راحت و بی دردسر کند. این مقاله مانند یک لغتنامه برای «یادگیری عمیق» میباشد که در هرکجا به واژهای برخوردید که نتوانستید مفهوم آن را بفهمید، به این مقاله مراجعه کنید.
برخی اصطلاحات یادگیری عمیق
برای اینکه درک اصطلاحات راحتتر باشد، آنها را به 3 گروه تقسیم کردهایم. اگر فقط دنبال یک مفهوم خاصی میگردید، میتوانید مستقیما آن را مطالعه کنید. ولی اگر در این موضوع تازه وارد هستید، مطالعه کل اصطلاحات به ترتیب، توصیه میشود.
- مقدمات شبکههای عصبی
- شبکههای عصبی کانولوشن
- شبکههای عصبی بازگشتی
1. مقدمات شبکههای عصبی
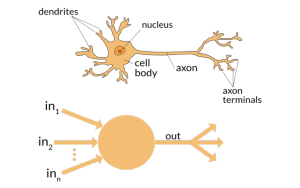
1) نورون
همانطور که عناصر اصلی مغز ما از نورونها تشکیل شدهاند، ساختار پایهی شبکههای عصبی نیز نورونها هستند. فقط کافیاست به این فکر کنید که وقتی ما اطلاعات جدیدی دریافت میکنیم، چکار میکنیم. وقتی اطلاعات را دریافت میکنیم، ابتدا آن را پردازش میکنیم و سپس یک خروجی بر اساس آن میسازیم. در زمینهی شبکههای عصبی نیز به همین شکل است.
یک نورون یک ورودی را میگیرد، آن را پردازش میکند و سپس یک خروجی تولید میکند که آن را یا برای پردازش بیشتر به سایر نورونها ارسال میکند، و یا خودش خروجی پایانی است.
2) وزن
هنگامی که یک ورودی وارد نورون میشود، توسط یک وزن (weight) بخشبندی میشود. برای مثال، اگر یک نورون دو ورودی داشته باشد، هر ورودی یک وزن مربوط به خود را دارد. مقداردهی اولیهی این وزنها به صورت شانسی صورت میگیرد و آنها در هنگام پروسهی یادگیری، بروزرسانی میشوند. پس از شروع فرایند یادگیری، شبکهی عصبی به ورودیهایی که از نظرش مهمتر هستند، وزن بیشتری را اختصاص میدهد. داشتن وزن صفر نشاندهندهی بی اهمیت بودن است.
فرض میکنیم که «a» ورودی، و «w1» وزن اختصاص داده شده به آن است. پس از عبور ورودی از گره (node)، تبدیل به a × W1 میشود.
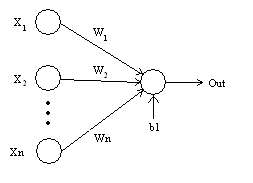
3) Bias
علاوه بر وزن، یکی دیگر از اجزای خطی که روی ورودی تاثیر میگذارد، «Bias» نام دارد. Bias به حاصل ضرب وزن در ورودی اضافه میشود. Bias درواقع به مقدار اضافه میشود تا محدودهی مقدار حاصل شده از ضرب وزن در ورودی را تغییر دهد. پس از اینکه Bias اضافه میشود، مقدار به a × W1+ bias تغییر پیدا میکند. Bias آخرین جزء خطی است که به تبدیل ورودی کمک میکند.
4) تابع فعالسازی
زمانی که کار اجزای خطی با ورودی تمام میشود، یک تابع غیر خطی به آن اعمال میشود. در این مرحله، تابع فعالسازی (Activation Function) کار خود را برروی حاصلی که از اجزای خطی به دست آمده است، انجام میدهد. این تابع سیگنالهای ورودی را به سیگنالهای خروجی تبدیل میکند. مقدار خروجی پس از اعمال تابع فعالسازی، چیزی شبیه به (f(a × W1+ bias میشود که ()f تابع فعالسازی است.
در نمودار زیر n ورودی به صورت X1 تا Xn به وزنهای مربوطه از Wk1 تا Wkn داده شدهاند. ابتدا وزنها در ورودیهای خودشان ضرب، و سپس با مقدار bias جمع میشوند. حاصل را u مینامیم.
u=∑w×x+b
سپس تابع فعالسازی برروی u اعمال میشود، یعنی (f(u، و در نهایت مقدار خروجی نهایی را به عنوان (Yk = f(u از نورون دریافت میکنیم.
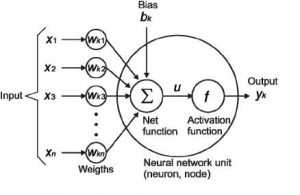
چندین تابع فعالسازی وجود دارند که از پرکاربردترین آنها میتوان «Sigmoid»، «ReLU» و «softmax» را نام برد.
الف) تابع Sigmoid
یکی از توابع فعالسازی که در بسیاری از جاها استفاده شده است، sigmoid است. این تابع به صورت زیر تعریف میشود:
(sigmoid(x) = 1/(1+e-x
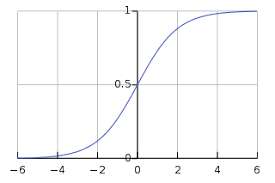
تابع sigmoid، مقادیر روانتری در محدودهی بین صفر و یک تولید میکند. البته شاید لازم باشد که تغییرات خروجی را با تغییرات کوچک در مقادیر ورودی، جبران کنیم. اینکار نیازمند داشتن نمودار منحنی است که تابع sigmoid ارائه میدهد، به همین جهت نسبت به توابع پلهای بهتر عمل میکنند.
ب) تابع ReLU
شبکههای جدید ترجیح میدهند به جای sigmoid، از توابع فعالسازی ReLU برای لایههای مخفی استفاده کنند. این تابع به صورت زیر تعریف میشود:
(f(x) = max(x,0
در این تابع، اگر مقدار X بزرگتر از صفر باشد، خروجی X است، و اگر مقدار X کوچکتر یا مساوی صفر باشد، خروجی صفر است. این تابع دارای شکل زیر است:
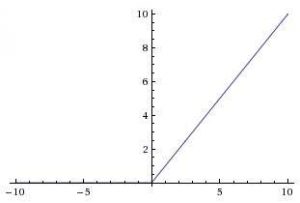
مزیت اصلی استفاده از ReLU این است که برای همهی ورودیهای بزرگتر از صفر، یک مشتق ثابت دارد. این مشتق ثابت به یادگیری شبکه سرعت میبخشد.
ج) تابع Softmax
توابع فعالسازی softmax معمولا در لایهی خروجی و برای مشکلات مربوط به دستهبندی استفاده میشوند. این تابع تقریبا شبیه به تابع sigmoid است، با تنها یک تفاوت که خروجیهای این تابع به گونهای نورمالسازی شدهاند که مجموع آنها عدد یک باشد. تابع sigmoid در مواقعی که ورودیهای ما از نوع دودویی (Binary) باشند عمل میکند، ولی در مواقعی که مشکلات مربوط به دستهبندی داشته باشیم، softmax کار دستهبندی هر مقدار را بسیار ساده میکند که در نهایت در احتمالات به ما کمک میکنند.
برای سادگی درک مفهوم، فرض کنید میخواهید یک عدد «6» را که کمی نیز شبیه «8» است، شناسایی کنید. این تابع همانند تصویر زیر به هر عدد، مقداری میدهد. در نهایت، به سادگی میتوانید ببینیم که بیشترین احتمال به «6» داده شدهاست و بالاترین احتمال بعدی «8» است و الی آخر.
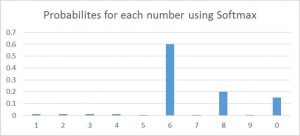
5) شبکهی عصبی
شبکههای عصبی نقش ستون فقرات را در «یادگیری عمیق» بازی میکنند. هدف شبکهی عصبی، تخمین یک تابع ناشناخته است. شبکهی عصبی توسط نورونهای به هم پیوسته تشکیل شدهاست. این نورونها دارای وزن و bias هستند که در هنگام یادگیری بر اساس خطاها، بروزرسانی میشود. تابع فعالسازی یک تبدیل غیر خطی برروی حاصل خطی ایجاد شده، انجام میدهد که خروجی را تولید کند. مجموع نورونهای فعالشده، خروجی را شکل میدهند. بهترین تعریف یک شبکهی عصبی را شخصی به نام «لیپینگ یانگ» (Liping Yang) ارائه میدهد. وی شبکهی عصبی را اینگونه تعریف کردهاست:
«شبکههای عصبی از چندین نورون مصنوعی تشکیل شده است که اطلاعات را بین یکدیگر رد و بدل میکنند، و هر کدام وزنهایی دارند که براساس «تجربهی» شبکه شکل میگیرند. نورونها یک نقطهی فعالسازی دارند که اگر مجموع وزن و دادههای ارسال شده به آنها از آن نقطه عبور کند، آنها فعال میشوند. مجموعهای از نورونهای فعال شده منجر به «یادگیری» میشوند.»
6) لایههای ورودی، خروجی و مخفی
همانطور که از اسمش پیداست، لایهی ورودی لایهای است که ورودی را دریافت میکند و قطعا لایهی اول شبکه است. لایهی خروجی لایهای است که خروجی را تولید میکند، یا همان لایهی پایانی شبکه است. لایههایی که کار پردازش را انجام میدهند، لایههای مخفی در شبکه هستند. این لایهها هستند که کارهای خاصی را برروی دادههایی که به آنها ارسال شده انجام میدهند و خروجی تولید شدهی خود را به لایههای بعدی ارسال میکنند. ما فقط میتوانیم لایههای ورودی و خروجی را ببینیم و لایههای میانی مخفی هستند.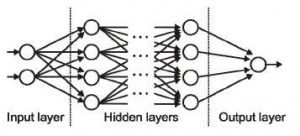
7) (MLP (Multi Layer Perceptron
یک نورون به تنهایی نمیتواند کارهای پیچیده و سنگین را انجام دهد. به همین خاطر، از پشتهای از نورونها برای تولید خروجی مورد نظر استفاده میکنیم (در سادهترین شبکهها، فقط یک لایهی ورودی، یک لایهی مخفی و یک لایهی خروجی وجود داشت). هر لایه شامل چندین نورون میشود و هر نورون در هر لایه، به تمام نورونهای لایهی بعد متصل است. به این شبکهها، شبکههای تمام متصل (fully connected networks) نیز میگویند.
8) تکثیر رو به جلو
تکثیر رو به جلو (Forward Propagation) به حرکت ورودی از درون لایهی مخفی به سمت لایهی خروجی اشاره دارد. در تکثیر رو به جلو، اطلاعات تنها به سمت جلو حرکت میکنند. لایهی ورودی، مقدار ورودی را به لایهی مخفی ارسال کرده و سپس خروجی تولید میشود. قدم به عقب در اینجا معنایی ندارد.
9) تابع هزینه
هنگامی که ما یک شبکه را شکل میدهیم، این شبکه سعی میکند که خروجی را هرچه دقیقتر پیشبینی کند. مقدار این دقت در شبکه توسط تابع هزینه (cost) به دست میآید. این تابع سعی میکند هنگامی که شبکه اشتباهی میکند، آن را جریمه کند. وقتی یک شبکه راهاندازی میکنیم، هدف ما این است که دقت پیشبینی را افزایش، و خطاها را کاهش دهیم تا نیاز به تابع هزینه کاهش یابد. بهینهترین خروجی، خروجیای است که کمترین میزان هزینه را داشته باشد. اگر بگوییم که تابع هزینه، مربع مقدار خطاها است، میتوانیم آن را به صورت زیر بنویسیم.
C= 1/m ∑(y – a)²
در اینجا m تعداد ورودیهای یادگیری، a مقدار پیشبینی شده، و y مقدار صحیح است. کل پروسهی یادگیری با هدف کاهش هزینه کار میکند.
10) شیب کاهشی
شیب کاهشی (Gradient Descent) یک الگوریتم بهینهسازی برای کاهش هزینه است. برای اینکه آن را بهتر درک کنید، به این مثال توجه کنید. هنگام پایین رفتن از یک تپه، به جای مستقیم پایین پریدن، باید با قدمهای کوچک پایین بروید. به همین دلیل، کاری که ما میکنیم این است که از نقطهی x شروع میکنیم، به مقدار کمی پایین میرویم (مقدار delta h)، و مکان خودمان را با مقدار x-delta h بروزرسانی میکنیم، و همینطور پایین میرویم تا به ته مسیر برسیم. ته مسیر را کمترین هزینه در نظر بگیرید.
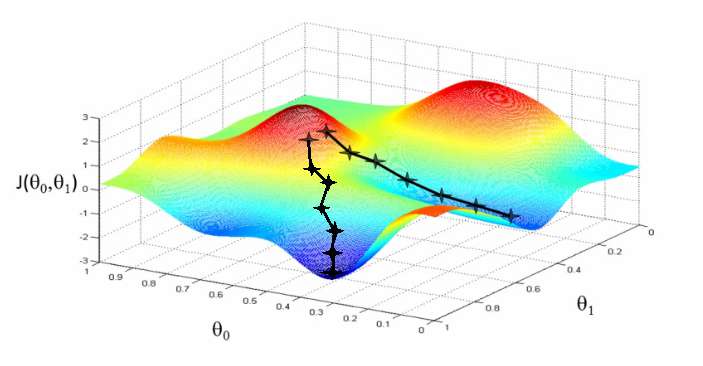
از نظر ریاضی، برای پیدا کردن مقدار مینیموم محلی (local minimum) یک تابع، باید قدمها را بر خلاف جهت شیب آن تابع برداشت.
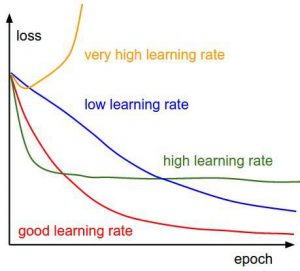
11) نسبت یادگیری
میزان کاهش هزینه در هر تکرار را نسبت یادگیری میگویند. به عبارت سادهتر، سرعت کاهش هزینهها همان نسبت یادگیری است. نسبت یادگیری را باید با دقت زیادی انتخاب کرد تا به اندازهای زیاد نباشد که حالت بهینه را رد کنیم و به اندازهای کم نباشد که یادگیری شبکه سالها زمان ببرد.
12) تکثیر به عقب
زمانی که ما یک شبکهی عصبی را تعریف میکنیم، مقدار وزن و bias را به صورت شانسی بین گرهها پخش میکنیم. هنگامی که خروجی یک کار را میگیریم، میتوانیم به کمک آن، مقدار خطای شبکه را محاسبه کنیم، سپس این مقدار را به همراه نمودار تابع هزینه به شبکه برگردانیم تا وزنهای شبکه بروزرسانی شوند. این وزنها به گونهای بروزرسانی میشوند که خطاهای مشابه کاهش پیدا کنند. به این عمل، تکثیر به عقب (back-propagation) میگویند.
در تکثیر به عقب، جهت حرکت شبکه رو به عقب است، خطا و نمودار به لایهی مخفی بازمیگردند تا وزنها براساس آنها بروزرسانی شوند.
13) بستهها
زمانی که داریم یک شبکهی عصبی را تعلیم میدهیم، به جای ارسال کل ورودی، آن را به بستههای کوچک با اندازهی یکسان تقسیم میکنیم. وقتی دادهها را به صورت بسته (Batch) ارسال میکنیم، باعث میشود مدل ما نسبت به مدلی که تمام اطلاعات را یکجا دریافت کرده است، جامعتر باشد.
14) دوره
یک دوره (Epoch) به یک تکثیر رفت و برگشت در شبکه اشاره دارد. یعنی یک دوره برابر با یک رفت و برگشت ورودی در کل شبکه است. تعداد دورههایی که برای یادگیری شبکه استفاده میکنید کاملا دست خودتان است. درست است که داشتن دورههای بیشتر منجر به دقت بیشتر در شبکه میشود، ولی زمان یادگیری شبکه را هم افزایش میدهد. به علاوه، باید توجه داشته باشید که اگر تعداد دورهها بیش از حد زیاد باشد، ممکن است هضم آن برای شبکه سنگین باشد، یا اصطلاحا شبکه «over-fit» شود.
15) Dropout
واژهی dropout در لغت به معنای بیرون رفتن یا رها کردن است. Dropout یک تکنیک است که جلوی «over-fit» شدن شبکه را میگیرد. همانطور که در اسمش پیداست، در هنگام یادگیری، برخی از نورونها به صورت شانسی رها میشوند. این بدین معنا است که یادگیری برروی معماریهای متفاوت با مجموعه نورونهای متفاوت صورت میگیرد. میتوانید به dropout به عنوان یک تکنیک گروهی نگاه کنید که در آن خروجی چندین شبکه مخلوط میشوند تا خروجی نهایی را شکل دهند.

16) نرمالسازی بستهها
از نظر مفهومی، میتوانیم به نرمالسازی بستهها به عنوان سدی نگاه کنیم که در بخشهای مختلفی از یک رود قرار گرفتهاست. اینکار باعث میشود مطمئن شویم که لایهی بعدی همان گونهای دادهها را دریافت میکند که انتظارش را دارد. در هنگام یادگیری شبکهی عصبی، وزنها پس از هر قدم در «شیب کاهشی»، تغییر پیدا میکنند. اینکار شکل دادهای که به لایهی بعدی میرود را تغییر میدهد.

هر لایه انتظار دارد که دادههایی مشابه دادههای قبلی خود دریافت کند، به همین دلیل ما هم قبل از ارسال دادهها، آنها را نرمالسازی میکنیم.
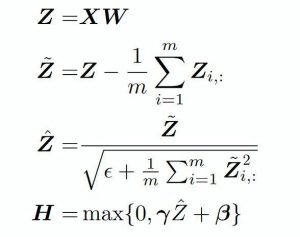
شبکههای عصبی کانولوشن
1) فیلترها
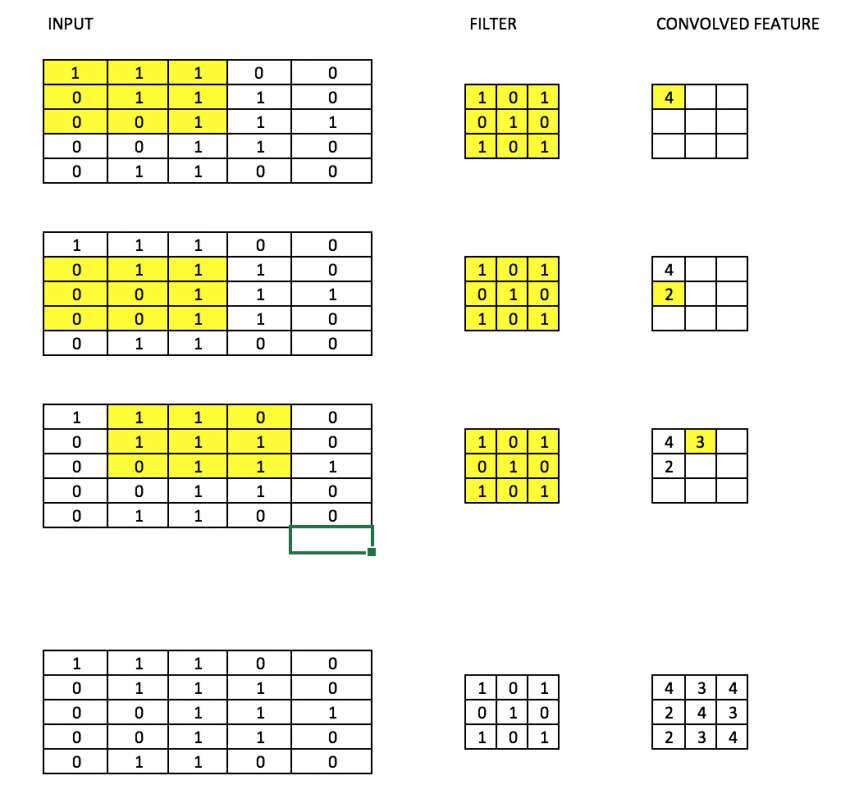
یک فیلتر در شبکههای کانولوشن (Convolutional) مانند یک وزن ماتریسی میماند که آن را در تصویر ورودی ضرب میکنیم تا یک خروجی حسابشده به دست آوریم. فرض کنید یک تصویر با سایز 28در28 داریم. یک فیلتر شانسی با سایز 3در3 برروی آن قرار میدهیم که بعدا در سایر بخشهای 3در3 تصویر ضرب شود تا یک خروجی حسابشده را تشکیل دهد. اندازهی فیلتر معمولا از اندازهی تصویر اصلی کوچکتر است. مقادیر فیلترها نیز مانند وزنها در هنگام تکثیر به عقب بروزرسانی میشوند تا هزینه را کاهش دهند.
تصویر زیر را فرض کنید. ما یک ماتریس 3در3 داریم که در تمام بخشهای 3در3 تصویر ضرب میشود تا مقدار حسابشده را تشکیل دهد.
2) (CNN (Convolutional neural network
شبکههای عصبی کانولوشن به صورت کلی برای ورودیهای تصویری استفاده میشوند. فرض کنید یک ورودی با اندازهی 28در28در3 داریم، اگر بخواهیم از شبکههای عصبی معمولی استفاده کنیم، 2,352 تا پارامتر 28در28در3 خواهیم داشت. هرچه هم که سایز تصویر بیشتر باشد، تعداد پارامترها بیشتر میشود. ما تصویر را به عبارتی در هم «میپیچیم» (معادل فارسی convolve) تا تعداد این پارامترها کاهش پیدا کند (همانند فیلتر که بالا دیدیم.) با حرکت دادن فیلتر در طول و عرض ورودی، یک نقشهی فعالسازی دو بعدی (2-demensional activation map) به دست میآوریم که درواقع حاصل ضرب فیلتر در همه جای ورودی است. ما این نقشهها را همراه با یک عمق روی هم قرار میدهیم تا مقدار خروجی را به دست آوریم.
برای درک واضحتر، تصویر زیر را مشاهده کنید.
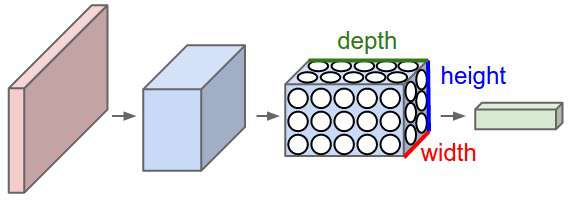
3) Pooling
زیاد پیش میآید که بین لایههای کانولوشن، لایههای «pooling» (که از نظر لغوی به معنای جمعآوری است) را نیز اضافه کنند. اینکار برای کاهش تعداد پارامترها و جلوگیری از «over-fitting» انجام میشود. بیشترین نوع استفاده شده از «Pooling»، استفاده از لایهی «pooling» با فیلتر 2در2 و عملیات ماکسیمومگیری است. نحوهی کار آن اینگونه است که بیشترین عدد هر ماتریس 4در4 را گرفته و در خروجی قرار میدهد.
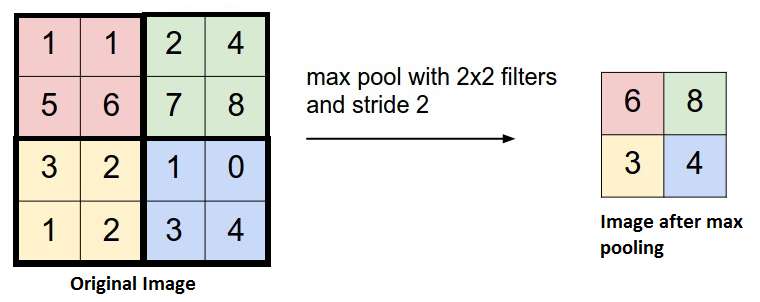
عملیات «pooling» را با عملگرهای دیگر نظیر میانگینگیری نیز میتوان انجام داد، ولی ماکسیمومگیری بیشترین درصد موفقیت را داشته است.
4) لایهسازی
لایهسازی (Padding) به معنای اضافه کردن لایههای اضافی با مقدار صفر دور تصویر است تا تصویر خروجی اندازهی یکسانی با ورودی داشته باشد. به این کار «لایهسازی یکسان» (Same Padding) میگویند.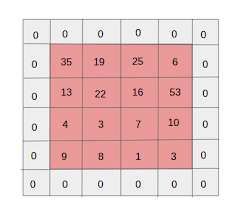
پس از اعمال لایهسازی یکسان، لایهای که در فیلترسازی خلاصه شدهاست، دارای اندازهی برابر با تصویر اصلی خواهد بود. «لایهسازی صحیح» (Valid Padding) به این اشاره دارد که تمامی پیکسلهای واقعی یا «صحیح» را نگهداری کنیم. در این حالت پس از اعمال فیلترها، اندازهی طول و عرض خروجی پس از هر لایهی کانولوشن، کاهش پیدا میکند.
5) تقویت دادهها
تقویت دادهها (Data Augmentation) با اضافه کردن دادههای جدید که از دادههای دریافتی حاصل شدهاست، اشاره دارد که ممکن است در پیشبینی ها موثر باشد. برای مثال، فرض کنید یک تصویر تاریک داریم که یک گربه در آن است. شاید با روشنتر کردن این تصویر، پیدا کردن گربه در آن سادهتر شود. یا مثلا یک عدد «9» را در نظر بگیرید که در یک تصویر کمی چرخیده یا کج است. در این حالت، چرخاندن تصویر مشکل را حل میکند و دقت را در مدل ما افزایش میدهد. با چرخاندن یا روشن کردن تصویر، ما داریم کیفیت دادههایمان را افزایش میدهیم. به این کار تقویت داده میگویند.
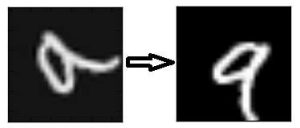
شبکههای عصبی بازگشتی
1) نورونهای بازگشتی
یک نورون بازگشتی نورونی است که خروجی آن t بار به خودش بازمیگردد. اگر به نمودار زیر نگاه کنید، خروجی نورون t بار به عنوان ورودی به خودش بازگشته است. این کار مانند این میماند که t نورون متفاوت را به هم وصل کرده باشیم. مزیت اصلی این نورون این است که خروجی جامعتری را ارائه میدهد.
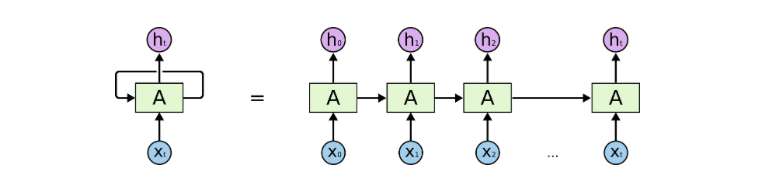
2) (RNN (Recurrent Neural Network
شبکههای عصبی بازگشتی (Recurrent Neural Network) برای دادههای ترتیبی استفاده میشوند که در آنها از خروجی قبلی، برای پیشبینی خروجی بعدی استفاده میشود. در این حالت، شبکهها در خودشان حلقههای تکرار دارند. این حلقهها که در نورونهای مخفی قرار دارند، بهشان این امکان را میدهند تا اطلاعات ورودیهای قبلی را برای مدتی ذخیره کنند تا بتوانند خروجیهای بعدی را پیشبینی کنند. خروجی لایهی مخفی مجددا t بار به لایهی مخفی ارسال میشود. این حالت تصویری شبیه به تصویر بالا است. خروجی یک نورون بازگشتی تنها زمانی به لایهی بعدی ارسال میشود که تعداد تکرار آن تمام شده باشد. در این حالت، خروجی جامعتر است و اطلاعات قبلی برای مدت بیشتری نگهداری میشوند.
در نهایت، خطاها براساس این بازگشتها تکثیر به عقب میشوند تا وزنها را بروزرسانی کنند.
به اینکار «تکثیر رو به عقب در زمان» (Back propagation through time یا به اختصار BPTT) میگویند.
3) مسالهی Vanishing Gradient
مسالهی Vanishing Gradient در شرایطی رخ میدهد که شیب حاصل شده از تابع فعالسازی خیلی کوچک باشد. در زمان تکثیر رو به عقب که وزنها در این شیبهای کوچک ضرب میشوند، معمولا به مقداری بسیار کوچک میرسند و هرچه در شبکه جلوتر میروند، در اصطلاح «ناپدید» میشوند. این امر باعث میشود که شبکه بسیاری از مقادیر را فراموش کند. این مساله در شبکههای عصبی بازگشتی مشکلساز میشوند که در آنها به یاد داشتن طولانی مدت اطلاعات بسیار مهم است.
4) مسالهی Exploding Gradient
این مساله کاملا برعکس مسالهی Vanishing Gradient است. در اینجا شیب حاصل از تابع فعالسازی زیادی بزرگ است. باعث میشود که در هنگام تکثیر به عقب، وزن یک گرهی خاص نسبت به بقیه گرهها بیش از اندازه بزرگ شود. این مساله به راحتی قابل حل است، تنها کافیاست که مقدار شیب را کوتاه کنیم تا از حد خاصی نگذرد.
اگر مایل به کسب اطلاعات بیشتر در این زمینه باشید، شاید آموزشهای زیر بتوانند برایتان مقید باشند:
- آموزش یادگیری عمیق (Deep learning)
- آموزش برنامه نویسی یادگیری عمیق با پایتون
- مجموعه آموزش های شبکه های عصبی مصنوعی در متلب
#









ممنون از توضیحات کاملتون. برای من خیلی مفید بود
ینی حقیقتا لذت بردم. عالی بود عالی. من برای پروژه دانشگام به این کلمات برخوردم و اینجا تونستم خیلی عالی درکشون کنم تا بتونم توی ارائه م قشنگتر موضوع رو انتقال بدم. حقیقتا ممنون از زحماتتون.
به نظرم متن خوبی بودش و توی برگردون کلمات نویسنده خوب کار کرده بود. هرچند کسی که توی این زمینه کار نکرده باشه کمی این مفاهیم ناآشنا شاید باشد.
عالی بود
مختصر و مفید
سلام
یه سوال ؟
اگه ما 20000 داده داشته باشیم batch ما 10 باشه یعنی دیتا به 10 بسته 2000تایی تقسیم شده؟
ممنون
اگر منظور از 10، سایز بچ هستش، نه. یعنی 2000 تا مینی بچ دارید که هر کدوم 10 تا داده دارند.
اگر منظور از 10، 10 تا بچ باشه، بله.
در ضمن در این حالت به این میگویم مینی بچ نه بچ.
عالی بود????
خیلی ممنون
عالی بود. واقعا نیاز بیشتری به اینجور اطلاعات راجع به یادگیری عمیق هست. ممنون
سلام
برای دانش ابتدایی از شبکه عصبی و شروع آن مطالب بسیار مفید است. تشکر
سلام.کاش رفرنس این مطالب هم میگذاشتید تا استفاده بیشتری ببریم.ممنون.
در زیر پست منبع رو ذکر کردند:
https://www.analyticsvidhya.com/blog/2017/05/25-must-know-terms-concepts-for-beginners-in-deep-learning/
جای این گونه از مطالب در وب پارسی خالی هست
ممنون از شما
عالی و بی نظیر بود. خوشحالم که چنین مطالب مفید و تخصصی رو به زبان فارسی میشه پیدا کرد.