در مباحث قبلی مجله فرادرس ، با سری توانی آشنا شدیم و حل معادلات دیفرانسیل با استفاده از روش سری توانی را بیان کردیم. دیدیم که سری توانی، کاربرد بسیار مهمی در حل معادلات دیفرانسیل دارد. در این آموزش از مجموعه آموزشهای ریاضی مجله فرادرس، درباره مشتق و انتگرال سری توانی بحث خواهیم کرد.
محتوای این مطلب جهت یادگیری بهتر و سریعتر آن، در انتهای متن به صورت ویدیویی نیز ارائه شده است.
مشتق و انتگرال سری توانی
سری توانی ∑ n = 0 ∞ a n x n \sum \limits _ { n = 0 } ^ \infty { { a _ n } { x ^ n } } n = 0 ∑ ∞ a n x n همگرایی آن R > 0 R \gt 0 R > 0
f ( x ) = ∑ n = 0 ∞ a n x n = a 0 + a 1 x + a 2 x 2 + … , ∣ x ∣ < R . \large { f \left ( x \right ) = \sum \limits _ { n = 0 } ^ \infty { { a _ n } { x ^ n } } } = { { a _ 0 } + { a _ 1 } x } + { { a _ 2 } { x ^ 2 } + \ldots , \; \; } \kern-0.3pt { \left | x \right | \lt R . } f ( x ) = n = 0 ∑ ∞ a n x n = a 0 + a 1 x + a 2 x 2 + … , ∣ x ∣ < R .
فرض کنید در ∣ x ∣ < R \left| x \right| \lt R ∣ x ∣ < R f ( x ) = ∑ n = 0 ∞ a n x n f \left ( x \right ) = \sum \limits _ { n = 0 } ^ \infty { { a _ n }{ x ^ n } } f ( x ) = n = 0 ∑ ∞ a n x n
f ’ ( x ) = d d x a 0 + d d x a 1 x + d d x a 2 x 2 + … = a 1 + 2 a 2 x + 3 a 3 x 2 + … = ∑ n = 1 ∞ n a n x n – 1 . \large { f ’ \left ( x \right ) } = { \frac { d } { { d x } } { a _ 0 } + \frac { d } { { d x } }{ a _ 1 } x } + { \frac { d } { { d x } } { a _ 2 } { x ^ 2 } + \ldots } \\ \large = { { a _ 1 } + 2 { a _ 2 } x + 3 { a _ 3 } { x ^ 2 } + \ldots } = { \sum \limits _ { n = 1 } ^ \infty { n { a _ n } { x ^ { n – 1 } } } . } f ’ ( x ) = d x d a 0 + d x d a 1 x + d x d a 2 x 2 + … = a 1 + 2 a 2 x + 3 a 3 x 2 + … = n = 1 ∑ ∞ n a n x n –1 .
همچنین میتوان جمله به جمله از سری توانی در بازه همگرایی انتگرال گرفت. بنابراین، اگر – R < b < x < R – R \lt b \lt x \lt R – R < b < x < R
∫ b x f ( t ) d t = ∫ b x a 0 d t + ∫ b x a 1 t d t + ∫ b x a 2 t 2 d t + … + ∫ b x a n t n d t + … \large { \int \limits _ b ^ x { f \left ( t \right ) d t } } = { \int \limits _ b ^ x { { a _ 0 } d t } + \int \limits _ b ^ x { { a _ 1 } t d t } } + { \int \limits _ b ^ x { { a _ 2 } { t ^ 2 } d t } + \ldots } + { \int \limits _ b ^ x { { a _ n } { t ^ n } d t } + \ldots } b ∫ x f ( t ) d t = b ∫ x a 0 d t + b ∫ x a 1 t d t + b ∫ x a 2 t 2 d t + … + b ∫ x a n t n d t + …
اگر از سری در بازه [ 0 , x ] \left[ {0,x} \right] [ 0 , x ]
∫ 0 x f ( t ) d t = ∫ 0 x a 0 d t + ∫ 0 x a 1 t d t + ∫ 0 x a 2 t 2 d t + … + ∫ 0 x a n t n d t + … = a 0 x + a 1 x 2 2 + a 2 x 3 3 + … = ∑ n = 0 ∞ a n x n + 1 n + 1 + C . \large { \int \limits _ 0 ^ x { f \left ( t \right ) d t } } = { \int \limits _ 0 ^ x { { a _ 0 } d t } + \int \limits _ 0 ^ x { { a _ 1 } t d t } } + { \int \limits _ 0 ^ x { { a _ 2 } { t ^ 2 } d t } + \ldots } + { \int \limits _ 0 ^ x { { a _ n } { t ^ n } d t } + \ldots } \\ \large = { { a _ 0 } x + { a _ 1 } \frac { { { x ^ 2 } } } { 2 } + { a _ 2 } \frac { { { x ^ 3 } } } { 3 } + \ldots } = { \sum \limits _ { n = 0 } ^ \infty { { a _ n } \frac { { { x ^ { n + 1 } } } } { { n + 1 } } } } + { C . } 0 ∫ x f ( t ) d t = 0 ∫ x a 0 d t + 0 ∫ x a 1 t d t + 0 ∫ x a 2 t 2 d t + … + 0 ∫ x a n t n d t + … = a 0 x + a 1 2 x 2 + a 2 3 x 3 + … = n = 0 ∑ ∞ a n n + 1 x n + 1 + C .
مثالها
در ادامه، چند مثال را بررسی میکنیم.
مثال ۱
نشان دهید تساوی زیر برقرار است.
1 1 + x = 1 – x + x 2 − x 3 + x 4 – … = ∑ n = 0 ∞ a n x n , ∣ x ∣ < 1. \large { \frac { 1 } { { 1 + x } } = 1 – x + { x ^ 2 } } - { { x ^ 3 } + { x ^ 4 } – \ldots } = { \sum \limits _ { n = 0 } ^ \infty { { a _ n } { x ^ n } } \; \; } \kern-0.3pt{\text{,}\;\;\left| x \right | \lt 1 . } 1 + x 1 = 1– x + x 2 − x 3 + x 4 – … = n = 0 ∑ ∞ a n x n , ∣ x ∣ < 1.
حل: ابتدا سری توانی زیر را در نظر بگیرید:
1 + x + x 2 + x 3 + … \large { 1 + x + { x ^ 2 } } + { { x ^ 3 } + \ldots } 1 + x + x 2 + x 3 + …
سری بالا، یک سری هندسی با قدر نسبت x x x ∣ x ∣ < 1 \left| x \right| \lt 1 ∣ x ∣ < 1 1 1 – x {\large\frac{1}{{1 – x}}\normalsize} 1– x 1 − x -x − x x x x
1 – x + x 2 − x 3 + … = 1 1 – ( – x ) = 1 1 + x , ∣ x ∣ < 1. \large { 1 – x + { x ^ 2 } } - { { x ^ 3 } + \ldots } = { \frac { 1 } { { 1 – \left ( { – x } \right ) } } } = { \frac { 1 } { { 1 + x } } \; \; } \kern-0.3pt{\text{,}\;\; \left | x \right | \lt 1 . } 1– x + x 2 − x 3 + … = 1– ( – x ) 1 = 1 + x 1 , ∣ x ∣ < 1.
بنابراین:
1 1 + x = 1 – x + x 2 − x 3 + x 4 – … = ∑ n = 0 ∞ ( – 1 ) n x n , ∣ x ∣ < 1. \large { \frac { 1 } { { 1 + x } } = 1 – x + { x ^ 2 } } - { { x ^ 3 } + { x ^ 4 } – \ldots } = { \sum \limits _ { n = 0 } ^ \infty { { { \left ( { – 1 } \right ) } ^ n } { x ^ n } } \; \; } \kern-0.3pt {\text{,} \; \; \left | x \right | \lt 1 . } 1 + x 1 = 1– x + x 2 − x 3 + x 4 – … = n = 0 ∑ ∞ ( –1 ) n x n , ∣ x ∣ < 1.
مثال ۲
سری توانی تابع کسری 1 2 – x \large\frac{1}{{2 – x}}\normalsize 2– x 1
حل: میتوانیم تابع را به صورت زیر بنویسیم:
1 2 – x = 1 2 1 – x 2 . \large \frac { 1 } { { 2 – x } } = \frac { { \frac { 1 } { 2 } } }{ { 1 – \frac { x } { 2 } } } . 2– x 1 = 1– 2 x 2 1 .
همانطور که میبینیم، عبارت بالا، مجموع یک سری هندسی بینهایت با جمله اول 1 2 {\large\frac{1}{2}\normalsize} 2 1 x 2 {\large\frac{x}{2}\normalsize} 2 x
1 2 + 1 2 x 2 + 1 2 ( x 2 ) 2 + 1 2 ( x 2 ) 3 + … = 1 2 + x 2 2 + x 2 2 3 + x 3 2 4 + … = ∑ n = 0 ∞ x n 2 n + 1 . \large { \frac { 1 } { 2 } + \frac { 1 } { 2 } \frac { x } { 2 } + \frac { 1 } { 2 } { \left ( { \frac { x } { 2 } } \right ) ^ 2 } } + { \frac { 1 } { 2 } { \left ( { \frac { x } { 2 } } \right ) ^ 3 } + \ldots } \\ \large = { \frac { 1 } { 2 } + \frac { x } { { { 2 ^ 2 } } } + \frac { { { x ^ 2 } } } { { { 2 ^ 3 } } } } + { \frac { {{ x ^ 3 } } } { { { 2 ^ 4 } } } + \ldots } = { \sum \limits _ { n = 0 } ^ \infty { \frac { { { x ^ n } } } { {{ 2 ^ { n + 1 } } } } } . } 2 1 + 2 1 2 x + 2 1 ( 2 x ) 2 + 2 1 ( 2 x ) 3 + … = 2 1 + 2 2 x + 2 3 x 2 + 2 4 x 3 + … = n = 0 ∑ ∞ 2 n + 1 x n .
سری توانی در ∣ x ∣ < 2 \left| x \right| \lt 2 ∣ x ∣ < 2
مثال ۳
سری توانی 6 x 5 x 2 – 4 x – 1 \large\frac{{6x}}{{5{x^2} – 4x – 1}}\normalsize 5 x 2 –4 x –1 6 x
حل: ابتدا تابع را به کسرهای جزئی بسط میدهیم. تابع درجه دوم مخرج را میتوان به صورت 5 x 2 – 4 x – 1 = ( 5 x + 1 ) ( x – 1 ) 5{x^2} – 4x – 1= \left( {5x + 1} \right)\left( {x – 1} \right) 5 x 2 –4 x –1 = ( 5 x + 1 ) ( x –1 )
6 x 5 x 2 – 4 x – 1 = A 5 x + 1 + B x – 1 . \large { \frac { { 6 x } } { { 5 { x ^ 2 } – 4 x – 1 } } } = { \frac { A } { { 5 x + 1 } } } + { \frac { B } { { x – 1 } } . } 5 x 2 –4 x –1 6 x = 5 x + 1 A + x –1 B .
با ضرب دو طرف تساوی بالا در 5 x 2 – 4 x – 1 = ( 5 x + 1 ) ( x – 1 ) 5{x^2} – 4x – 1= \left( {5x + 1} \right)\left( {x – 1} \right) 5 x 2 –4 x –1 = ( 5 x + 1 ) ( x –1 )
$$ \large { { 6 x } = { A \left ( { x – 1 } \right ) } + { B \left ( { 5 x + 1 } \right ) , \; \; } } \Rightarrow<br />
{ { 6 x } = { A x – A } + { 5 B x + B , \; \; } }\\ \large \Rightarrow<br />
{ { 6 x } = { \left ( { A + 5 B } \right ) x } + { \left ( { – A + B } \right ) , \; \; } } \Rightarrow<br />
{ \left\{ { \begin {array} { * { 2 0 } {l} }<br />
{ A + 5 B = 6 } \\<br />
{ – A + B = 0 }<br />
\end {array} } \right . . } $$
جواب دستگاه بالا، A = 1 A=1 A = 1 B = 1 B=1 B = 1
6 x 5 x 2 – 4 x – 1 = 1 5 x + 1 + 1 x – 1 = 1 1 + 5 x − 1 1 – x . \large { \frac { { 6 x } } { { 5 { x ^ 2 } – 4 x – 1 } } } = { \frac { 1 } { { 5 x + 1 } } } + { \frac { 1 } { { x – 1 } } } = { \frac { 1 } { { 1 + 5 x } } } - { \frac { 1 } { { 1 – x } } . } 5 x 2 –4 x –1 6 x = 5 x + 1 1 + x –1 1 = 1 + 5 x 1 − 1– x 1 .
دو کسر سمت راست تساوی بالا، مجموع سریهای هندسی بینهایت هستند:
1 1 + 5 x = 1 1 – ( – 5 x ) = 1 – 5 x + ( – 5 x ) 2 + ( – 5 x ) 3 + … = ∑ n = 0 ∞ ( – 5 x ) n , \large { \frac { 1 } { { 1 + 5 x } } } = { \frac { 1 } { { 1 – \left ( { – 5 x } \right ) } } } = { 1 – 5 x + { \left ( { – 5 x } \right ) ^ 2 } } + { { \left ( { – 5 x } \right ) ^ 3 } + \ldots } = { \sum \limits _ { n = 0 } ^ \infty { { { \left ( { – 5 x } \right ) } ^ n } } , } 1 + 5 x 1 = 1– ( –5 x ) 1 = 1–5 x + ( –5 x ) 2 + ( –5 x ) 3 + … = n = 0 ∑ ∞ ( –5 x ) n ,
1 1 – x = 1 + x + x 2 + x 3 + … = ∑ n = 0 ∞ x n . \large { \frac { 1 } { { 1 – x } } } = { 1 + x + { x ^ 2 } } + { { x ^ 3 } + \ldots } = { \sum \limits _ { n = 0 } ^ \infty { { x ^ n } } . } 1– x 1 = 1 + x + x 2 + x 3 + … = n = 0 ∑ ∞ x n .
بنابراین، بسط سری توانی تابع اصلی برابر است با:
6 x 5 x 2 – 4 x – 1 = ∑ n = 0 ∞ ( – 5 x ) n – ∑ n = 0 ∞ x n = ∑ n = 0 ∞ [ ( – 5 x ) n – x n ] = ∑ n = 0 ∞ [ ( – 5 ) n – 1 ] x n . \large { \frac { { 6 x } } { { 5 { x ^ 2 } – 4 x – 1 } } } = { \sum \limits _ { n = 0 } ^ \infty { { { \left ( { – 5 x } \right ) } ^ n } } – \sum \limits _ { n = 0 } ^ \infty { { x ^ n } } } \\ \large = { \sum \limits _ { n = 0 } ^ \infty { \left[ { { { \left ( { – 5 x } \right ) } ^ n } – { x ^ n } } \right]} } = { \sum \limits _ { n = 0 } ^ \infty { \left [ { { { \left ( { – 5 } \right ) } ^ n } – 1 } \right ] { x ^ n } } . } 5 x 2 –4 x –1 6 x = n = 0 ∑ ∞ ( –5 x ) n – n = 0 ∑ ∞ x n = n = 0 ∑ ∞ [ ( –5 x ) n – x n ] = n = 0 ∑ ∞ [ ( –5 ) n –1 ] x n .
مثال ۴
یک نمایش سری توانی برای تابع ln ( 1 + x ) \ln \left( {1 + x} \right) ln ( 1 + x ) ∣ x ∣ < 1 \left| x \right| \lt 1 ∣ x ∣ < 1
حل: در مثال ۱، بسط سری توانی زیر را به دست آوردیم:
1 1 + x = 1 – x + x 2 − x 3 + … = ∑ n = 0 ∞ ( – 1 ) n x n , ∣ x ∣ < 1. \large { \frac { 1 } { { 1 + x } } } = { 1 – x + { x ^ 2 } } - { { x ^ 3 } + \ldots } = { \sum \limits _ { n = 0 } ^ \infty { { { \left ( { – 1 } \right ) } ^ n } { x ^ n } } , \; \; } \kern-0.3pt { \left | x \right | \lt 1 . } 1 + x 1 = 1– x + x 2 − x 3 + … = n = 0 ∑ ∞ ( –1 ) n x n , ∣ x ∣ < 1.
با انتگرالگیری جمله به جمله در بازه [ 0 , x ] \left[ {0,x} \right] [ 0 , x ]
ln ( 1 + x ) = ∫ 0 x d t 1 + t = ∫ 0 x ( 1 – t + t 2 – t 3 + … ) d t = x – x 2 2 + x 3 3 − x 4 4 + … = ∑ n = 0 ∞ ( – 1 ) n x n + 1 n + 1 = ∑ n = 1 ∞ ( – 1 ) n + 1 x n n . \large { \ln \left ( { 1 + x } \right ) } = { \int \limits _ 0 ^ x { \frac { { d t } } { { 1 + t } } } } = { \int \limits _ 0 ^ x { \left ( { 1 – t + { t ^ 2 } – { t ^ 3 } + \ldots } \right ) d t } } \\ \large = { x – \frac { { { x ^ 2 } } } { 2 } + \frac { { { x ^ 3 } } } { 3 } } - { \frac { { { x ^ 4 } } } { 4 } + \ldots } = { \sum \limits _ { n = 0 } ^ \infty { \frac { { { { \left ( { – 1 } \right ) } ^ n } { x ^ { n + 1 } } } } { { n + 1 } } } } = { \sum \limits _ { n = 1 } ^ \infty { \frac { { { { \left ( { – 1 } \right ) } ^ { n + 1 } } { x ^ n } } } { n } } . } ln ( 1 + x ) = 0 ∫ x 1 + t d t = 0 ∫ x ( 1– t + t 2 – t 3 + … ) d t = x – 2 x 2 + 3 x 3 − 4 x 4 + … = n = 0 ∑ ∞ n + 1 ( –1 ) n x n + 1 = n = 1 ∑ ∞ n ( –1 ) n + 1 x n .
مثال ۵
انتگرال ∫ 0 x ln ( 1 + t ) t d t \int\limits_0^x {{\large\frac{{\ln \left( {1 + t} \right)}}{t}\normalsize} dt} 0 ∫ x t ln ( 1 + t ) d t
حل: در مثال قبلی (مثال ۴)، بسط سری توانی تابع لگاریتمی را به دست آوردیم:
ln ( 1 + t ) = ∑ n = 1 ∞ ( – 1 ) n + 1 t n n = t – t 2 2 + t 3 3 − t 4 4 + … , ∣ t ∣ < 1. \large { \ln \left ( { 1 + t } \right ) } = { \sum \limits _ { n = 1 } ^ \infty { \frac { { { { \left ( { – 1 } \right ) } ^ { n + 1 } } { t ^ n } } } { n } } } = { t – \frac { { { t ^ 2 } } } { 2 } + \frac { { { t ^ 3 } } } { 3 } } - { \frac { { { t ^ 4 } } } { 4 } + \ldots , \; \; } \kern-0.3pt{\left| t \right| \lt 1 . } ln ( 1 + t ) = n = 1 ∑ ∞ n ( –1 ) n + 1 t n = t – 2 t 2 + 3 t 3 − 4 t 4 + … , ∣ t ∣ < 1.
در نتیجه، میتوانیم بنویسیم:
ln ( 1 + t ) t = ∑ n = 1 ∞ ( – 1 ) n + 1 t n – 1 n = 1 – t 2 + t 2 3 − t 3 4 + … \large {\frac{{\ln \left( {1 + t} \right)}}{t} } = {\sum\limits_{n = 1}^\infty {\frac{{{{\left( { – 1} \right)}^{n + 1}}{t^{n – 1}}}}{n}} } = {1 – \frac{t}{2} + \frac{{{t^2}}}{3} }-{ \frac{{{t^3}}}{4} + \ldots } t ln ( 1 + t ) = n = 1 ∑ ∞ n ( –1 ) n + 1 t n –1 = 1– 2 t + 3 t 2 − 4 t 3 + …
با انتگرالگیری جمله به جمله از سری در بازه [ 0 , x ] \left[ {0,x} \right] [ 0 , x ]
∫ 0 x ln ( 1 + t ) t d t = ∫ 0 x [ 1 – t 2 + t 2 3 – t 3 4 + … ] d t = x – x 2 2 ⋅ 2 + x 3 3 ⋅ 3 − x 4 4 ⋅ 4 + … = ∑ n = 1 ∞ ( – 1 ) n + 1 x n n 2 . \large \begin {align*} \int\limits_0^x {\frac{{\ln \left( {1 + t} \right)}}{t}dt} & = {\int\limits_0^x {\left[ {1 – \frac{t}{2} + \frac{{{t^2}}}{3} – \frac{{{t^3}}}{4} + \ldots } \right]dt} } \\ & = {x – \frac{{{x^2}}}{{2 \cdot 2}} + \frac{{{x^3}}}{{3 \cdot 3}} }-{ \frac{{{x^4}}}{{4 \cdot 4}} + \ldots } \\ & = {\sum\limits_{n = 1}^\infty {\frac{{{{\left( { – 1} \right)}^{n + 1}}{x^n}}}{{{n^2}}}} .} \end {align*} 0 ∫ x t ln ( 1 + t ) d t = 0 ∫ x [ 1– 2 t + 3 t 2 – 4 t 3 + … ] d t = x – 2 ⋅ 2 x 2 + 3 ⋅ 3 x 3 − 4 ⋅ 4 x 4 + … = n = 1 ∑ ∞ n 2 ( –1 ) n + 1 x n .
مثال ۶
نمایش سری توانی تابع نمایی e x e^x e x
حل: سری زیر را در نظر بگیرید:
f ( x ) = ∑ n = 0 ∞ x n n ! = 1 + x + x 2 2 ! + x 3 3 ! + … \large { f \left ( x \right ) = \sum \limits _ { n = 0 } ^ \infty { \frac { { { x ^ n } } } { { n ! } } } } = { 1 + x + \frac { { { x ^ 2 } } } { {2 ! } } } + { \frac { { { x ^ 3 } }} { { 3 ! } } + \ldots } f ( x ) = n = 0 ∑ ∞ n ! x n = 1 + x + 2 ! x 2 + 3 ! x 3 + …
که به ازای همه مقادیر x x x
با مشتقگیری از تک تک جملات سری، داریم:
f ’ ( x ) = d d x 1 + d d x x + d d x x 2 2 ! + d d x x 3 3 ! + … = 0 + 1 + x + x 2 2 ! + … = f ( x ) . \large { f ’ \left ( x \right ) } = { \frac { d } { { d x } } 1 + \frac { d } { { d x } } x + \frac { d } { { d x } } \frac { { { x ^ 2 } } } { { 2 ! }} } + { \frac { d } { { d x } } \frac { { { x ^ 3 } } } { { 3 ! } } + \ldots } \\ \large = { 0 + 1 + x } + { \frac { { { x ^ 2 } } } { { 2 ! } } + \ldots } = { f \left ( x \right ) . } f ’ ( x ) = d x d 1 + d x d x + d x d 2 ! x 2 + d x d 3 ! x 3 + … = 0 + 1 + x + 2 ! x 2 + … = f ( x ) .
بنابراین، تابع f ( x ) f(x) f ( x ) f ’ = f f’ = f f ’ = f f ( x ) = c e x f\left( x \right) = c{e^x} f ( x ) = c e x c c c f ( 0 ) = 1 f\left( 0 \right) = 1 f ( 0 ) = 1 c = 1 c=1 c = 1 e x e^x e x
f ( x ) = e x = ∑ n = 0 ∞ x n n ! = 1 + x + x 2 2 ! + x 3 3 ! + … \large { f \left ( x \right ) = { e ^ x } = \sum \limits _ { n = 0 } ^ \infty { \frac { { { x ^ n } } } { { n ! } } } } = { 1 + x + \frac { { { x ^ 2 } } } { { 2 ! } } } + { \frac { { { x ^ 3 } } } { { 3 ! } } + \ldots } f ( x ) = e x = n = 0 ∑ ∞ n ! x n = 1 + x + 2 ! x 2 + 3 ! x 3 + …
مثال ۷
بسط سری توانی تابع سینوس هیپربولیک sinh x \sinh x sinh x
حل: از آنجایی که sinh x = e x – e – x 2 \sinh x = {\large\frac{{{e^x} – {e^{ – x}}}}{2}\normalsize} sinh x = 2 e x – e – x e x e^x e x e − x e^{-x} e − x
در مثال قبل، فرمول زیر را محاسبه کردیم:
e x = ∑ n = 0 ∞ x n n ! = 1 + x + x 2 2 ! + x 3 3 ! + … \large { { e ^ x } = \sum \limits _ { n = 0 } ^ \infty { \frac { { { x ^ n } } } { {n ! } } } } = { 1 + x + \frac { { { x ^ 2 } } } { { 2 ! } } } + { \frac { { { x ^ 3 } } } { { 3 ! } } + \ldots } e x = n = 0 ∑ ∞ n ! x n = 1 + x + 2 ! x 2 + 3 ! x 3 + …
با قرار دادن − x -x − x x x x
e – x = ∑ n = 0 ∞ ( – x ) n n ! = ∑ n = 0 ∞ ( – 1 ) n x n n ! = 1 – x + x 2 2 ! − x 3 3 ! + … \large { { e ^ { – x } } = \sum \limits _ { n = 0 } ^ \infty { \frac { { { { \left ( { – x } \right ) } ^ n } } } { { n ! } } } } = { \sum \limits _ { n = 0 } ^ \infty { \frac { { { { \left ( { – 1 } \right ) } ^ n } { x ^ n } } } { { n ! } } } } = { 1 – x + \frac { { { x ^ 2 } } } { { 2 ! } } } - { \frac { { { x ^ 3 } } } { { 3 ! } } + \ldots } e – x = n = 0 ∑ ∞ n ! ( – x ) n = n = 0 ∑ ∞ n ! ( –1 ) n x n = 1– x + 2 ! x 2 − 3 ! x 3 + …
در نهایت، بسط تابع سینوس هیپربولیک را مینویسیم:
sinh x = e x – e – x 2 = 1 2 [ ∑ n = 0 ∞ x n n ! − ∑ n = 0 ∞ ( – x ) n n ! ] = 1 2 [ ( 1 + x + x 2 2 ! + x 3 3 ! + … ) − ( 1 – x + x 2 2 ! – x 3 3 ! + … ) ] = 1 2 [ 2 ( x + x 3 3 ! + x 5 5 ! + … ) ] = x + x 3 3 ! + x 5 5 ! + … = ∑ n = 0 ∞ x 2 n + 1 ( 2 n + 1 ) ! . \large { \sinh x = \frac { { { e ^ x } – { e ^ { – x } } } } { 2 } } = { \frac { 1 } { 2 }\left [ { \sum \limits _ { n = 0 } ^ \infty { \frac { { { x ^ n } } } { { n ! } } } } \right . } - { \left . { \sum \limits _ { n = 0 } ^ \infty { \frac { { { { \left ( { – x } \right ) } ^ n } }} { { n ! } } } } \right ] } \\ \large = { \frac { 1 } { 2 } \left [ { \left ( { 1 + x + \frac { { { x ^ 2 } } } { { 2 ! } } + \frac { { { x ^ 3 } } } { { 3 ! } } + \ldots } \right ) } \right . } - { \left . { \left ( { 1 – x + \frac { { { x ^ 2 } } } { { 2 ! } } – \frac { { { x ^ 3 } } } { { 3 ! } } + \ldots } \right ) } \right] } \\ \large = { \frac { 1 } { 2 } \left [ { 2 \left ( { x + \frac { { { x ^ 3 } } } { { 3 ! } } + \frac { { { x ^ 5 } } } { { 5 ! } } + \ldots } \right ) } \right ] } = { x + \frac { { { x ^ 3 } } } { { 3 ! } } + \frac { { { x ^ 5 } } } { { 5 ! } } + \ldots } = { \sum \limits _ { n = 0 } ^ \infty { \frac { { { x ^ { 2 n + 1 } } } } { { \left ( { 2 n + 1 } \right ) ! } } } . } sinh x = 2 e x – e – x = 2 1 n = 0 ∑ ∞ n ! x n − n = 0 ∑ ∞ n ! ( – x ) n = 2 1 [ ( 1 + x + 2 ! x 2 + 3 ! x 3 + … ) − ( 1– x + 2 ! x 2 – 3 ! x 3 + … ) ] = 2 1 [ 2 ( x + 3 ! x 3 + 5 ! x 5 + … ) ] = x + 3 ! x 3 + 5 ! x 5 + … = n = 0 ∑ ∞ ( 2 n + 1 ) ! x 2 n + 1 .
فیلم های آموزش مشتق و انتگرال سری توانی – به زبان ساده (+ دانلود فیلم آموزش رایگان) فیلم آموزشی سری توانی فیلم آموزشی مشتق سری توانی فیلم آموزشی انتگرال سری توانی 
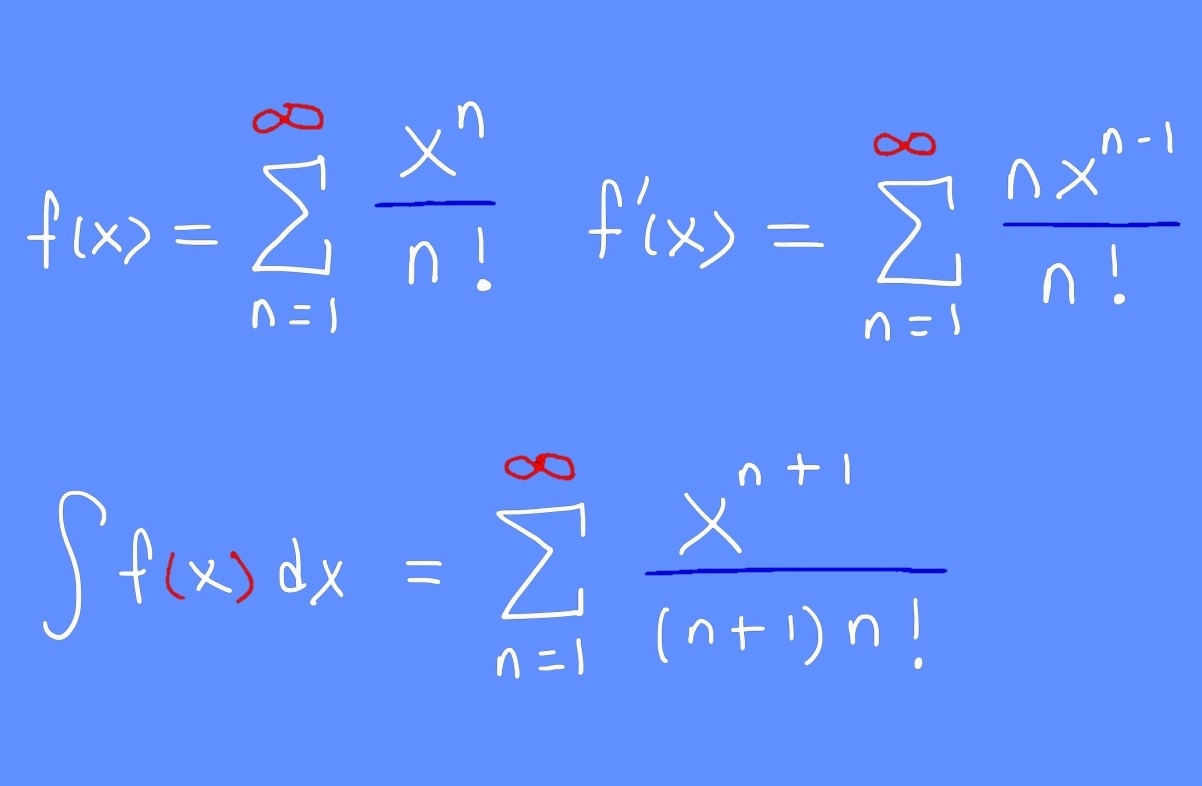













اگر بازه انتگرال گیری نامتناهی باشه چی؟ فرض کنیم سری مورد نظرمون روی تمام xهای بزرگ یا مساوی صفر همگرا باشه و ما بخوایم از این سری بر همان بازه صفر تا مثبت بی نهایت انتگرال بگیریم. آیا انتگرال گیری مجازه؟
سلام و وقت بخیر؛
در صورت همگرایی یکنواخت سری، امکان انتگرالگیری در بازه 0 تا بینهایت وجود دارد.
از همراهی شما با مجله فرادرس سپاسگزاریم.
آموزنده بود
مثال 3 خیلی جالب بود
سلام مهدی عزیز.
سپاس از همراهیتان با مجله فرادرس.
سالم و سربلند باشید.