روابط بین سینوس و کسینوس – تمام فرمول ها + مثال و تمرین

روابط مثلثاتی که با عنوان توابع مثلثاتی یا نسبت‌های مثلثاتی نیز شناخته می‌شوند، انواع روابط بین زاویه‌ها و طول اضلاع یک مثلث قائم‌الزاویه را بیان می‌کنند. این روابط به ما کمک می‌کنند تا بتوانیم اندازه‌های زاویه‌ای را به اندازه‌های طولی و برعکس تبدیل کنیم. نحوه تعریف این روابط با استفاده از جدول دایره مثلثاتی انجام می‌شود. در این مطلب از مجله فرادرس قصد داریم به بررسی بخشی از مهم‌ترین روابط مثلثاتی یعنی روابط بین سینوس و کسینوس بپردازیم.

مهم ترین روابط بین سینوس و کسینوس

مهم‌ترین روابط بین سینوس و کسینوس در جدول زیر آورده شده‌اند.

سینوس و کسینوس چیست؟

اولین قدم برای یادگیری روابط بین سینوس و کسینوس این است که تعریف این دو تابع مثلثاتی را بشناسیم. سینوس و کسینوس اصلی‌ترین توابع مثلثاتی هستند که بر اساس نسبت‌های اضلاع یک مثلث قائم‌الزاویه تعریف می‌شوند. دقت کنید این تعاریف برای زاویه‌های حاده یا تند (زاویه‌هایی که بزرگتر از صفر و کوچکتر از$$90 ^\circ$$ هستند) صادق‌اند و اساس تمام روابط مثلثاتی دیگر را تشکیل می‌دهند.

فرض کنید یک مثلث قائم‌الزاویه داریم که یکی از زاویه‌های تند آن را با $$\theta$$ نشان می‌دهیم. در این صورت اضلاع مختلف به شکل زیر نام‌گذاری می‌شوند:

• وتر: بلندترین ضلع که همیشه روبروی زاویه $$90 ^\circ$$ قرار دارد.
• ضلع مقابل وتر: ضلعی که روبروی زاویه $$\theta$$ قرار دارد.
• ضلع مجاور وتر: ضلعی که کنار زاویه $$\theta$$ قرار دارد (به جز وتر).

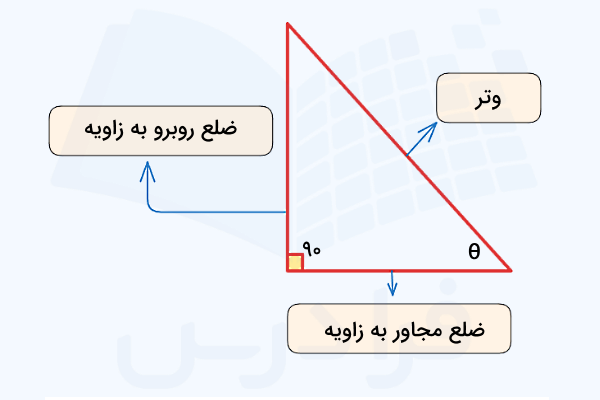
به این ترتیب تعریف سینوس و کسینوس بر اساس این اضلاع به شرح زیر خواهد شد:

• سینوس زاویه $$\theta$$ یا $$\sin \theta$$: نسبت طول ضلع مقابل زاویه $$\theta$$ به طول وتر در مثلث قائم‌الزاویه است.
• کسینوس زاویه $$\theta$$ یا $$\cos \theta$$: نسبت طول ضلع کنار زاویه $$\theta$$ به طول وتر در مثلث قائم‌الزاویه است.

وتر / ضلع مقابل $$\sin \theta =$$

وتر / ضلع مجاور $$\cos \theta =$$

به زبان ساده، این توابع به ما می‌گویند که اگر اندازه یک زاویه در یک مثلث قائم‌الزاویه مشخص باشد، نسبتی که بین اضلاع آن مثلث برقرار است، چقدر خواهد بود. برای مثال، اگر در یک مثلث قائم‌الزاویه طول ضلع مقابل زاویه‌ای $$3$$ واحد، طول ضلع مجاور آن $$4$$ واحد و طول وتر $$5$$ واحد باشد، در این صورت سینوس و کسینوس آن زاویه به ترتیب برابر‌اند با:

$$\sin \theta = \frac{3}{5}$$

$$\cos \theta = \frac{4}{5}$$

نکته: علاوه بر این دو تابع مثلثاتی مهم، توابع دیگری مانند تانژانت یا $$\tan \theta$$ و کتانژانت یا $$\cot \theta$$ را نیز داریم که پرداختن به آن‌ها از موضوع این مطلب خارج است.

دامنه و برد سینوس و کسینوس

در درس ریاضی دامنه یک تابع مثلثاتی به این معنا است که چه اعدادی را می‌توانیم به عنوان ورودی یا زاویه به توابعی مانند سینوس و کسینوس بدهیم. برد نیز معادل است با نتایج یا اعداد خروجی حاصل از توابع مثلثاتی مانند سینوس و کسینوس. در مورد دامنه قادریم هر زاویه‌ای شامل مثبت، منفی، بزرگ یا کوچک را برای سینوس و کسینوس در نظر بگیریم. بنابراین دامنه سینوس و کسینوس مجموعه اعداد حقیقی است.

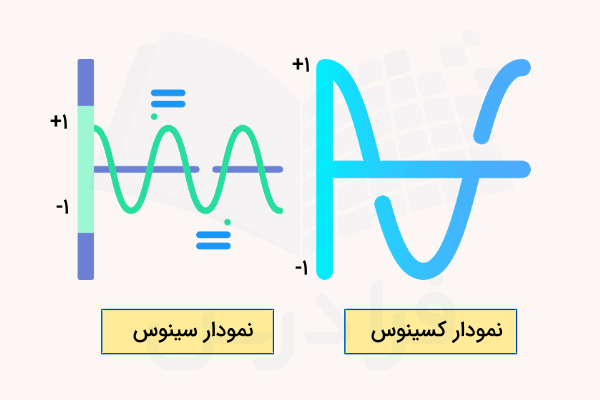
همچنین اگر به نمودار این دو تابع یا به دایره مثلثاتی بیشتر دقت کنیم، می‌بینیم که این توابع هرگز مقداری بزرگتر از یک ندارند. به عبارت دیگری خروجی یا برد سینوس و کسینوس همیشه بین $$-1$$ و $$1$$ در نوسان است:

$$-1 \leq \sin \theta \leq +1$$

$$-1 \leq \cos \theta \leq +1$$

یادگیری سینوس و کسینوس با فرادرس

با درک عمیق‌تر مفاهیمی مانند سینوس و کسینوس یک زاویه و روش به دست آوردن آن‌ها بر اساس جدول دایره مثلثاتی، می‌توانید به راحتی مسائل پیچیده‌تر را حل کنید. توابع مثلثاتی نه تنها در هندسه، بلکه در علومی مانند فیزیک و مهندسی نیز کاربرد گسترده‌ای دارند. برای مثال مدل‌سازی پدیده‌های تناوبی در فیزیک با استفاده از این توابع انجام می‌شود و علت آن ماهیت تناوبی این توابع است که در فواصل منظم تکرار می‌شوند. در همین زمینه، مشاهده فیلم‌های آموزشی زیر از مجموعه فرادرس راهنمای جامعی برای یادگیری مثلثات محسوب می‌شود:

• فیلم آموزش رایگان سینوس، کسینوس و تانژانت + محاسبه نسبت‌ های مثلثاتی فرادرس
• فیلم آموزش رایگان محاسبه نسبت های مثلثاتی + ۸ رابطه مهم فرادرس
• فیلم آموزش رایگان معادلات مثلثاتی ریاضی (دوازدهم) + روش حل با مثال فرادرس
• فیلم آموزش رایگان توابع مثلثاتی در ریاضی ۲ – پایه یازدهم علوم تجربی فرادرس
• فیلم آموزش رایگان روابط مثلثاتی در مثلث قائم الزاویه + مثال فرادرس

سینوس و کسینوس در دایره مثلثاتی

دایره مثلثاتی یا دایره واحد ابزار اساسی مثلثات است که به ما کمک می‌کند تا توابع مثلثاتی مانند سینوس و کسینوس را برای تمامی زوایه‌ها از جمله زوایای بزرگتر از $$90 ^\circ$$ یا حتی زاویه‌های منفی تعریف کنیم. بنابراین برای اینکه با روابط بین سینوس و کسینوس بهتر آشنا شویم، لازم است ابتدا با اجزای این دایره مهم آشنا شویم:

• مرکز: مرکز این دایره دقیقا روی مبدا دستگاه مختصات دکارتی یعنی نقطه $$(0,0)$$ قرار دارد.
• شعاع: شعاع این دایره برابر با یک واحد در نظر گرفته می‌شود و به همین دلیل به آن دایره واحد نیز می‌گویند.

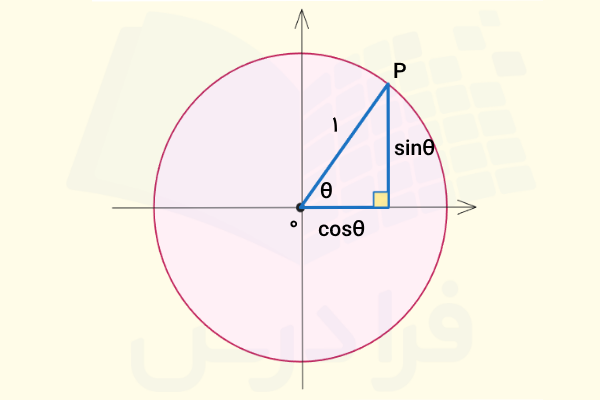
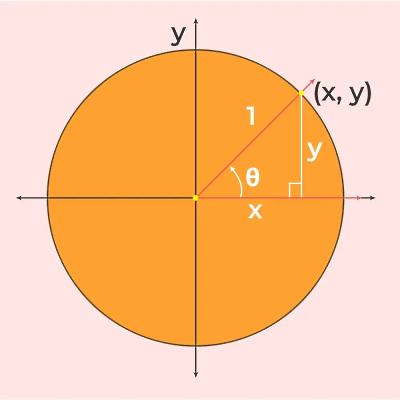
این دایره محل قرارگیری تمام نقاطی است که مختصات آن‌ها مرتبط است به سینوس و کسینوس زاویه‌ای که ایجاد می‌کنند. اگر زاویه‌ای مانند $$\theta$$ را در نظر بگیریم که ضلع ابتدایی آن بر روی محور مثبت افقی قرار دارد و ضلع انتهایی‌ آن دایره مثلثاتی را در نقطه $$P(x,y)$$ قطع کند، داریم:

• $$\cos \theta$$: طول افقی یا همان مختصات x نقطه $$P$$ است. بنابراین کسینوس بر روی محور افقی نمایش داده می‌شود.
• $$\sin \theta$$: طول عمودی یا همان مختصات y نقطه $$P$$ است. بنابراین سینوس بر روی محور عمودی نمایش داده می‌شود.

$$\Rightarrow P(x,y) = (\cos \theta, \sin \theta)$$

تعیین علامت سینوس و کسینوس در ربع ها

در بخش قبل و در آغاز بررسی روابط بین سینوس و کسینوس، دیدیم که دستگاه مختصات دایره مثلثاتی را به چهار ناحیه یا ربع مختلف تقسیم می‌کند. همان‌طور که در جدول زیر ملاحظه می‌کنید، علامت سینوس و کسینوس در هر ربع متفاوت است:

بنابراین همواره سینوس در نیمه بالایی دایره مثلثاتی یعنی ربع اول و دوم مثبت است، در حالی که کسینوس در نیمه سمت راست دایره مثلثاتی یعنی ربع اول و چهارم مثبت است. به این ترتیب مقادیر سینوس و کسینوس یا همان x و yها در یک دایره مثلثاتی برای زاویه‌های مختلف مطابق شکل زیر است:

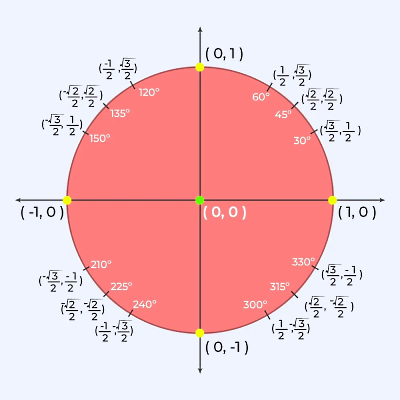
برای مثال، مقادیر سینوس و کسینوس زاویه $$\ 45^ \circ$$ یا $$\frac{\pi}{4}$$ رادیان برابر‌ است با $$\frac{\sqrt{2}}{2}$$ و $$\frac{\sqrt{2}}{2}$$، در حالی که مختصات x و y یا همان مقادیر سینوس و کسینوس برای نقطه‌ای که در زاویه $$\ 210^ \circ$$ این دایره واقع شده معادل است با $$(-\frac{\sqrt{3}}{2}, -\frac{1}{2})$$.

اتحاد اصلی مثلثات

پس از اینکه در بخش‌های قبل با اصول پایه یادگیری و درک مفهوم سینوس و کسینوس آشنا شدیم، در این بخش و بخش‌های بعد به معرفی روابط بین سینوس و کسینوس خواهیم پرداخت. اولین رابطه که با عنوان رابطه طلایی یا قضیه فیثاغورس مثلثاتی نیز شناخته می‌شود، مهم‌ترین و بنیادی‌ترین رابطه در مثلثات است که از قضیه فیثاغورس ناشی می‌شود. این رابطه به شکل زیر است:

$$\sin^2 \theta + \cos^2 \theta = 1$$

این فرمول بیان می‌کند که مجموع مربع سینوس یک زاویه و مربع کسینوس همان زاویه همواره برابر با عدد یک است، صرف‌نظر از اینکه زاویه $$\theta$$ چه مقداری داشته باشد. اثبات این قضیه بر پایه دایره مثلثاتی یا دایره واحد انجام می‌شود. فرض کنید نقطه‌ای به نام $$P$$ با مختصات $$(x,y)$$ روی دایره مثلثاتی قرار دارد و توسط زاویه $$\theta$$ ایجاد شده است. حالا اگر از این نقطه عمودی بر محور x رسم کنیم، یک مثلث قائم‌الزاویه ایجاد می‌شود. اضلاع این مثلث طبق شکل بخش قبل به شکل زیر هستند:

• طول افقی یا ضلع مجاور به زاویه $$\theta$$ برابر است با $$x = \cos \theta$$.
• طول عمودی یا ضلع مجاور به زاویه $$\theta$$ برابر است با $$y = \sin \theta$$.
• وتر این مثلث همان شعاع دایره است که در دایره مثلثاتی همواره برابر با یک واحد در نظر گرفته می‌شود.

حالا بر اساس قضیه فیثاغورس در مثلث قائم‌الزاویه داریم:

$$x^2 + y^2 = 1 \Rightarrow sin^2 \theta + \cos^2 \theta= 1$$

به این ترتیب طبق روابط زیر می‌توانیم با داشتن سینوس یک زاویه کسینوس آن را پیدا کنیم و برعکس:

$$\sin \theta = \pm \sqrt{1- \cos^2 \theta}$$

$$\cos \theta = \pm \sqrt{1- \sin^2 \theta}$$

سینوس و کسینوس زاویه های متمم

می‌دانیم زاویه‌های متمم به هر دو زاویه‌ای گفته می‌شود که مجموع آن‌ها برابر با $$\ 90^ \circ$$ یا $$\frac{\pi}{2}$$ رادیان باشد. روابط بین سینوس و کسینوس برای زوایای متمم به این شکل است:

• سینوس یک زاویه همواره برابر است با کسینوس زاویه متمم آن:

$$\sin(\theta) = \cos(\frac{\pi}{2} - \theta)$$

• کسینوس یک زاویه همواره برابر است با سینوس زاویه متمم آن:

$$\cos(\theta) = \sin(\frac{\pi}{2} - \theta)$$

این روابط نیز به طور مستقیم از روابط مثلث قائم‌الزاویه به دست می‌آیند. می‌دانیم در هر مثلث قائم‌الزاویه مجموع دو زاویه تند برابر است با $$\ 90^ \circ$$ یا $$\frac{\pi}{2}$$ رادیان. پس اگر یکی از این زاویه‌ها $$\theta$$ باشد، زاویه دیگر حتما $$\frac{\pi}{2} - \theta$$ خواهد بود. همچنین گفتیم سینوس زاویه $$\theta$$ برابر است با اندازه ضلع مقابل به این زاویه تقسیم بر اندازه وتر.

از طرفی کسینوس زاویه $$\frac{\pi}{2} - \theta$$ نیز برابر می‌شود با اندازه ضلع مجاور به این زاویه تقسیم بر اندازه وتر. از دید زاویه $$\frac{\pi}{2} - \theta$$ ضلع مجاور معادل است با ضلع مقابل زاویه $$\theta$$. پس این دو نسبت با هم برابر خواهند شد و داریم $$\sin(\theta) = \cos(\frac{\pi}{2} - \theta)$$. علاوه بر دو رابطه بالا، بهتر است فرمول‌های زیر را نیز به خاطر داشته باشید:

$$-\sin \theta = \cos(\frac{\pi}{2} + \theta)$$

$$\cos \theta = \sin(\frac{\pi}{2} + \theta)$$

$$-\sin \theta = \cos(\frac{3\pi}{2} - \theta)$$

$$-\cos \theta = \sin(\frac{3\pi}{2} - \theta)$$

$$\sin \theta = \cos(\frac{3\pi}{2} + \theta)$$

$$-\cos \theta = \sin(\frac{3\pi}{2} + \theta)$$

سینوس و کسینوس زاویه های مکمل

در ادامه یادگیری روابط بین سینوس و کسینوس، فرمول‌های سینوس و کسینوس زاویه‌های مکمل هم را بررسی می‌کنیم. این روابط به ما کمک می‌کنند تا توابع مثلثاتی زاویه‌های بزرگتر از $$\ 90^ \circ$$ یا $$\frac{\pi}{2}$$ رادیان را به توابع مثلثاتی زاویه‌های تند تبدیل کنیم. می‌دانیم زاویه‌های مکمل به هر دو زاویه‌ای گفته می‌شود که مجموع آن‌ها برابر با $$\ 180^ \circ$$ یا $$\pi$$ رادیان شود. در مورد زاویه‌های مکمل سینوس و کسینوس طبق قواعد زیر محاسبه می‌شوند:

• علامت سینوس زاویه مکمل تغییر نمی‌کند:

$$\sin(\theta) = \sin(\pi - \theta)$$

• علامت کسینوس زاویه مکمل قرینه می‌شود:

$$\cos(\theta) = - \cos(\pi - \theta)$$

دقت کنید زاویه $$\pi - \theta$$ در ربع دوم قرار می‌گیرد و در این ناحیه ارتفاع y یا سینوس مثبت است، اما طول x یا کسینوس منفی است. به همین شکل نقاط متناظر آن‌ها نسبت به محور y نیز متقارن هستند، پس مختصات y آن‌ها یکسان و مختصات x آن‌ها قرینه است. در کنار این دو فرمول، پیشنهاد می‌کنیم روابط زیر را نیز به خاطر داشته باشید:

$$-\sin(\theta) = \sin(\pi + \theta)$$

$$-\cos(\theta) = \cos(\pi + \theta)$$

$$-\sin(\theta) = \sin(2\pi - \theta)$$

$$\cos(\theta) = \cos(2\pi - \theta)$$

$$\sin(\theta) = \sin(2\pi + \theta)$$

$$\cos(\theta) = \cos(2\pi + \theta)$$

سینوس و کسینوس زاویه های قرینه

زاویه قرینه یا $$-\theta$$ زاویه‌ای است که با زاویه اصلی یا $$\theta$$ از نظر مقدار برابر است، اما در جهت عقربه‌های ساعت یا در جهت منفی رسم شده است. در مورد زاویه‌های قرینه روابط بین سینوس و کسینوس بر اساس قوانین زیر نوشته می‌شوند:

• سینوس یک زاویه قرینه، قرینه می‌شود، چون سینوس یک تابع فرد است:

$$\sin (-\theta) = - \sin \theta$$

• کسینوس یک زاویه قرینه تغییر نمی‌کند، چون کسینوس یک تابع زوج است:

$$\cos (-\theta) = \cos \theta$$

دقت کنید چون زاویه $$-\theta$$ در ربع چهارم قرار می‌گیرد (با این فرض که زاویه $$\theta$$ در ربع اول باشد)، پس نقاط متناظر آن‌ها نسبت به محور x متقارن هستند. بنابراین مختصات x یا کسینوس آن‌ها یکسان و مختصات y یا سینوس آن‌ها قرینه است.

سینوس و کسینوس مجموع یا تفاضل

در ادامه بررسی روابط بین سینوس و کسینوس، می‌رسیم به بررسی فرمول‌های سینوس (یا کسینوس) مجموع (یا تفاضل) دو زاویه برای دو زاویه دلخواه مانند $$\alpha$$ و $$\beta$$:

• سینوس مجموع دو زاویه یا $$\sin (\alpha + \beta)$$:

$$\sin (\alpha + \beta) = \sin \alpha \cos \beta + \cos \alpha \sin \beta$$

• سینوس تفاضل دو زاویه یا $$\sin (\alpha - \beta)$$:

$$\sin (\alpha - \beta) = \sin \alpha \cos \beta - \cos \alpha \sin \beta$$

با مشاهده فیلم آموزش حسابان ۱ – پایه یازدهم فرادرس می‌توانید همراه با حل سوالات متنوع به این فرمول‌ها بهتر مسلط شوید:

دقت کنید در سینوس مجموع و تفاضل دو زاویه، در قالب دو جمله مختلف حاصل‌ضرب سینوس و کسینوس هر کدام از دو زاویه با هم ترکیب می‌شوند. اگر سینوس مجموع داشتیم، علامت بین این دو جمله مثبت و اگر سینوس تفاضل داشتیم، علامت بین دو جمله منفی خواهد شد. در مورد کسینوس مجموع (یا تفاضل) دو زاویه دلخواه $$\alpha$$ و $$\beta$$ نیز روابط به شکل زیر هستند:

• کسینوس مجموع دو زاویه یا $$\cos (\alpha + \beta)$$:

$$\cos (\alpha + \beta) = \cos \alpha \cos \beta - \sin \alpha \sin \beta$$

• کسینوس تفاضل دو زاویه یا $$\cos (\alpha - \beta)$$:

$$\sin (\alpha - \beta) = \cos \alpha \cos \beta + \sin \alpha \sin \beta$$

دقت کنید در مورد کسینوس لازم است ابتدا خودش را در خودش (کسینوس در کسینوس) و سپس سینوس را در سینوس ضرب کرده و در دو جمله قرار دهیم. سپس علامت بین این دو جمله را عکس علامت اولیه در نظر می‌گیریم، یعنی اگر کسینوس مجموع را می‌خواهیم از علامت منفی و اگر کسینوس تفاضل را می‌خواهیم از علامت مثبت استفاده می‌کنیم.

مجموع یا تفاضل سینوس و کسینوس

اتحادهای تبدیل مجموع به ضرب فرمول‌های مثلثاتی هستند که به ما کمک می‌کنند تا مجموع یا تفاضل توابع مثلثاتی مانند سینوس یا کسینوس را به صورت حاصل‌ضرب بیان کنیم. چهار فرمول اصلی برای روابط بین سینوس و کسینوس در این مبحث به شرح زیر خواهد بود:

• مجموع و تفاضل سینوس‌ها:

$$\sin A + \sin B = 2 \sin (\frac{A+B}{2})\cos (\frac{A-B}{2})$$

$$\sin A - \sin B = 2 \cos (\frac{A+B}{2})\sin (\frac{A-B}{2})$$

• مجموع و تفاضل کسینوس‌ها:

$$\cos A + \cos B = 2 \cos (\frac{A+B}{2})\cos (\frac{A-B}{2})$$

$$\cos A - \cos B = -2 \sin (\frac{A+B}{2})\sin (\frac{A-B}{2})$$

حاصل ضرب سینوس و کسینوس

در ادامه حاصل‌ضرب توابع مثلثاتی سینوس و کسینوس را می‌توانیم به صورت مجموع یا تفاضل آن‌ها بیان کنیم. این فرمول‌ها زمانی استفاده می‌شوند که ما حاصل‌ضرب سینوس و کسینوس با زوایای متفاوت مانند $$\sin A \cos B$$ را داریم و می‌خواهیم آن‌ها را برای ساده‌سازی یا انتگرال‌گیری به شکل جمع یا تفریق بنویسیم:

• حاصل‌ضرب سینوس و کسینوس:

$$\sin A \cos B = \frac{1}{2} [\sin(A+B) + \sin (A - B) ]$$

$$\cos A \sin B = \frac{1}{2} [\sin(A+B) - \sin (A - B) ]$$

• حاصل‌ضرب دو سینوس یا دو کسینوس:

$$\sin A \sin B = \frac{1}{2} [\cos(A-B) - \cos (A +B) ]$$

$$\cos A \cos B = \frac{1}{2} [\cos(A+B) + \cos (A - B) ]$$

سینوس و کسینوس زاویه های دو برابر

روابط بین سینوس و کسینوس در مورد زاویه‌های دو برابر یا زاویه‌ مضاعف را می‌توان حالت خاصی از روابط مجموع دو زاویه در نظر گرفت. کافی است در فرمول‌های بخش قبل، هر کدام از دو زاویه $$\alpha$$ و $$\beta$$ را برابر با $$\theta$$ در نظر بگیریم:

• سینوس دو برابر زاویه $$\theta$$ یا سینوس مضاعف:

$$\sin (\theta + \theta) = \sin \theta \cos \theta + \cos \theta \sin \theta = 2 \sin \theta \cos \theta$$

$$\sin (2\theta) = 2 \sin \theta \cos \theta$$

• کسینوس دو برابر زاویه $$\theta$$ یا کسینوس مضاعف:

$$\cos (\theta + \theta) = \cos \theta \cos \theta - \sin \theta \sin \theta= \cos^2 \theta - \sin^2 \theta$$

$$\cos (2\theta )= \cos^2 \theta - \sin^2 \theta$$

البته فرمول $$\cos (2\theta )$$ را می‌توانیم به شکل دیگری نیز بنویسیم، کافی است از اتحاد اصلی در مثلثات یعنی $$\sin^2 \theta + \cos^2 \theta = 1$$ استفاده کنیم و بجای $$\sin^2 \theta$$ عبارت $$1- \cos^2 \theta$$ را قرار دهیم:

$$\cos (2\theta ) = \cos^2 \theta - (1- \cos^2 \theta)$$

$$\cos (2\theta ) = 2 \cos^2 \theta - 1$$

و با جایگذاری $$1- \sin^2 \theta$$ بجای $$\cos^2 \theta$$ خواهیم داشت:

$$\cos (2\theta ) = 1- \sin^2 \theta - \sin^2 \theta$$

$$\cos (2\theta ) = 1-2 \sin^2 \theta$$

سینوس و کسینوس زاویه های سه برابر

روابط بین سینوس و کسینوس در مورد سه برابر یک زاویه برای ساده‌سازی و حل معادلات مثلثاتی پیچیده بکار می‌روند:

$$\sin (3 \theta ) = 3\sin\theta -4 \sin^3 \theta$$

$$\cos (3 \theta ) = 4\cos^3\theta -3 \cos \theta$$

سینوس و کسینوس نصف زاویه

فرمول‌های سینوس و کسینوس نیم‌زاویه مستقیما از روابط بین سینوس و کسینوس زاویه مضاعف که در بخش‌های قبل توضیح دادیم، استخراج می‌شوند. کافی است زاویه اصلی را $$\theta$$ در نظر بگیریم و روابط را برای $$\frac{\theta}{2}$$ بنویسیم:

$$\sin\frac{\theta}{2} = \pm \sqrt{\frac{1-\cos \theta}{2}}$$

$$\cos\frac{\theta}{2} = \pm \sqrt{\frac{1+\cos \theta}{2}}$$

آرک سینوس و آرک کسینوس

در توابع مثلثاتی یک زاویه را به تابع می‌دهیم و تابع به ما یک عدد (نسبت بین اضلاع) را می‌دهد. برای مثال، $$\sin 30^\circ = 0.5$$. اما در توابع مثلثاتی معکوس، این روند برعکس می‌شود و هدف این است که ببینیم کدام زاویه است که سینوس آن $$0.5$$ می‌شود. پاسخ این سوال همان تابع معکوس سینوس است که به صورت $$\sin^{-1} 0.5$$ یا $$arc \sin 0.5$$ نمایش داده می‌شود. در واقع توابع معکوس به دو صورت نمایش داده می‌شوند:

• استفاده از توان منفی یک: $$\sin^{-1} \theta$$ و $$\cos^{-1} \theta$$
• استفاده از پیشوند آرک: $$arc\sin \theta$$ و $$arc\cos \theta$$

نکته ۱: دقت کنید عبارت $$\sin^{-1} \theta$$ را نباید با عبارت $$\frac{1}{\sin \theta}$$ اشتباه گرفت. توان $$-1$$ در اینجا نماد تابع معکوس است.

در مورد دامنه و برد معکوس سینوس و کسینوس توجه به نکات زیر خیلی مهم است. می‌دانیم توابع مثلثاتی متناوب هستند، یعنی مقادیر آن‌ها پیوسته تکرار می‌شود. برای مثال، $$\sin 30^\circ = \sin 150^\circ = \sin 390^\circ =0.5$$. حالا اگر طبق تعریف توابع معکوس بخواهیم بدانیم سینوس چه زاویه‌ای برابر می‌شود با $$0.5$$، بی‌نهایت پاسخ مانند $$30^\circ ,150^\circ , 390^\circ, ...$$ خواهیم داشت. مشکل اینجاست که اگر یک تابع تمام این‌ اعداد را به عنوان پاسخ در نظر بگیرد، دیگر طبق تعریف ریاضیات، تابع محسوب نمی‌شود، چون برای یک ورودی چند خروجی داده است.

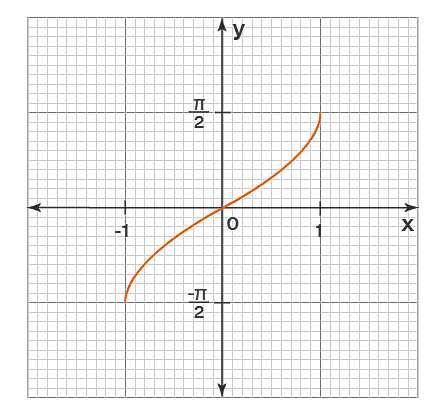
برای حل این مسئله لازم است دامنه را محدود کنیم، به این صورت که بخشی از نمودار سینوس و کسینوس را که در آن مقادیر تکراری وجود ندارند، برش می‌دهیم. پس باید تابع در آن بازه یک‌ به‌ یک باشد. در این روند فقط بازه‌ای از سینوس یا کسینوس را انتخاب می‌کنیم که از کمترین مقدار یعنی $$-1$$ تا بیشترین مقدار یعنی $$+1$$ را شامل شود، بدون اینکه مقادیر تکرار شوند.

این بازه استاندارد برای تابع آرک سینوس فاصله $$[-90^\circ, +90^\circ]$$ یا به رادیان $$[-\frac{\pi}{2}, +\frac{\pi}{2}]$$ را به عنوان خروجی می‌دهد. پس برد تابع آرک‌ سینوس همواره زاویه‌ای در ربع اول یا چهارم است. در مورد تابع آرک کسینوس نیز خروجی در بازه $$[0, 180^\circ]$$ یا به رادیان $$[0, \pi]$$ (ربع اول یا دوم) قرار می‌گیرد.

نکته ۲: اگر سینوس یا کسینوس را با معکوس خودشان ترکیب کنیم، هم را خنثی می‌کنند:

$$\sin (\arcsin \theta ) = \theta$$

$$\cos (\arccos \theta ) = \theta$$

معکوس سینوس و کسینوس زاویه های متمم

همان‌طور که روابط بین سینوس و کسینوس زوایای متمم با هم برابر بود، مجموع آرک‌های این دو تابع نیز عدد ثابتی معادل $$90^\circ$$ را نتیجه می‌دهد، یعنی داریم:

$$\arcsin \theta + \arccos \theta = \frac{\pi}{2}$$

این رابطه برای هر $$\theta$$ در بازه $$[-1, +1]$$ صادق است.

معکوس سینوس و کسینوس زاویه های قرینه

برای آرک سینوس و ارک کسینوس قرینه یک زاویه روابط زیر را داریم:

$$\sin^{-1} (-\theta) = - \sin^{-1} \theta$$

$$\cos^{-1} (-\theta) =\pi - \cos^{-1} \theta$$

یادگیری مثلثات در حسابان با فرادرس

در ریاضیات متوسطه دوم از توابع مثلثاتی در عملیاتی مانند بررسی آهنگ تغییرات، مشتق‌گیری و محاسبه انتگرال بسیار استفاده می‌شود. به همین دلیل در این قسمت قصد داریم چند فیلم‌‌ آموزشی در مورد این کتاب درسی به شما معرفی کنیم که در مجموعه فرادرس تهیه شده‌اند. مشاهده این فیلم‌ها به شما کمک می‌کند تا با بهره‌گیری از آموزش تصویری و حل مثال‌ها و تمرین‌های متنوع به مباحثی مانند مشتق توابع مثلثاتی یا توابع معکوس مثلثاتی و ... کاملا مسلط شوید:

• فیلم آموزش حسابان پایه یازدهم – حل تمرین فرادرس
• فیلم آموزش رایگان قضیه اساسی حسابان در حساب دیفرانسیل و انتگرال فرادرس
• فیلم آموزش حسابان پیشرفته فرادرس

حل مثال و تمرین از روابط بین سینوس و کسینوس

در بخش‌های قبل با تمام روابط بین سینوس و کسینوس آشنا شدیم. در این بخش به شما کمک می‌کنیم تا با حل چند نمونه سوال به کاربرد این روابط در حل مسائل مثلثات کاملا مسلط شوید. پیش از شروع، پیشنهاد می‌کنیم مطلب «روابط مثلثاتی و فرمول های مثلثاتی مهم + دانلود PDF خلاصه رایگان» از مجله فرادرس را نیز مطالعه کنید.

مثال ۱

اگر $$\sin \theta \cos \theta = 8$$ باشد، حاصل $$(\sin \theta + \cos \theta )^2$$ چقدر است؟

پاسخ

اگر $$(\sin \theta + \cos \theta )^2$$ را به شکل $$(x + y )^2$$ در نظر بگیریم، با کمک گرفتن از اتحاد مربع دو جمله‌ای می‌توانیم آن را به شکل $$(x + y )^2 = x^2 + y^2 + 2xy$$ بنویسیم:

$$(\sin \theta + \cos \theta )^2 = \sin^2 \theta + \cos^2 \theta + 2 \sin \theta \cos\theta$$

با توجه به اینکه $$\sin^2 \theta + \cos^2 \theta =1$$ است و طبق صورت سوال $$\sin \theta \cos \theta = 8$$، پس داریم:

$$\Rightarrow (\sin \theta + \cos \theta )^2 = 1 + 2 \times 8= 1+ 16 = 17$$

مثال ۲

اگر زاویه $$y$$ در ربع دوم قرار داشته باشد و بدانیم مقدار $$\cos y = \frac{5}{13}$$ است، $$\sin y$$ چقدر است؟

 پاسخ

برای حل این سوال باید از رابطه‌ای استفاده کنیم که در آن $$\sin y$$ و $$\cos y$$ را داشته باشیم. بهترین انتخاب اتحاد اصلی مثلثات یعنی $$\sin^2 y + \cos^2 y =1$$ است. پس داریم:

$$\sin^2 y + \cos^2 y =1$$

$$\Rightarrow \sin^2 y = 1- \cos^2 y = 1-(\frac{5}{13})^2$$

$$\Rightarrow \sin^2 y = 1-\frac{25}{169}=\frac{144}{169}$$

$$\Rightarrow \sin y = \pm \frac{12}{13}$$

اما برای اینکه علامت درستی را انتخاب کرده باشیم، لازم است به این نکته توجه کنیم که طبق صورت سوال زاویه $$y$$ در ربع دوم است و می‌دانیم سینوس در ربع دوم همواره مثبت است. پس علامت صحیح، علامت مثبت است:

$$\Rightarrow \sin y = + \frac{12}{13}$$

مثال ۳

حاصل $$\frac{1}{1-\cos x}+ \frac{1}{1+\cos x}$$ را بر حسب سینوس به دست آورید:

پاسخ

ابتدا دو کسر داده شده را با گرفتن مخرج مشترک با هم جمع می‌کنیم:

$$\frac{1}{1-\cos x}+ \frac{1}{1+\cos x} = \frac{1+\cos x + 1-\cos x}{(1-\cos x) (1+\cos x)}$$

با ساده کردن جملات صورت و استفاده از اتحاد مزدوج برای مخرج حاصل به شکل زیر خواهد شد:

$$\Rightarrow \frac{2}{(1-\cos x) (1+\cos x)} =\frac{2}{1-\cos^2 x}$$

در نهایت طبق فرمول اصلی مثلثات یعنی $$\sin^2 x + \cos^2 x =1$$ می‌توانیم $$1 - \cos^2 x$$ را به شکل $$\sin^2 x$$ بنویسیم:

$$\frac{1}{1-\cos x}+ \frac{1}{1+\cos x} =\frac{2}{\sin^2 x}$$

مثال ۴

مقدار $$x$$ در معادله $$\sin 2x = \cos( x-30^\circ)$$ چقدر است؟

پاسخ

با کمک گرفتن از رابطه $$\cos x= \sin90^\circ- x$$ سمت دیگر این تساوی را به شکل زیر می‌نویسیم:

$$\sin 2x = \sin[ 90^\circ -(x-30^\circ)]$$

$$\sin 2x = \sin[ 90^\circ -x+30^\circ] = \sin[ 120^\circ -x]$$

$$\Rightarrow 2x = 120^\circ -x \Rightarrow 3x = 120^\circ$$

$$\Rightarrow x = 40^\circ$$

مثال ۵

عبارت $$\frac{\sin 4a + \sin 2a}{\cos a}$$ را ساده کنید:

پاسخ

با استفاده از رابطه $$\sin A + \sin B = 2 \sin (\frac{A+B}{2})\cos (\frac{A-B}{2})$$ می‌توانیم عبارت بالا را ساده کنیم. کافی است $$A = 4a$$ و $$B = 2a$$ در نظر بگیریم:

$$\sin 4a + \sin 2a = 2 \sin (\frac{6a}{2})\cos (\frac{2a}{2}) = 2\sin 3a\cos a$$

$$\Rightarrow \frac{\sin 4a + \sin 2a}{\cos a} = \frac{2\sin 3a\cos a}{\cos a} = 2\sin 3a$$