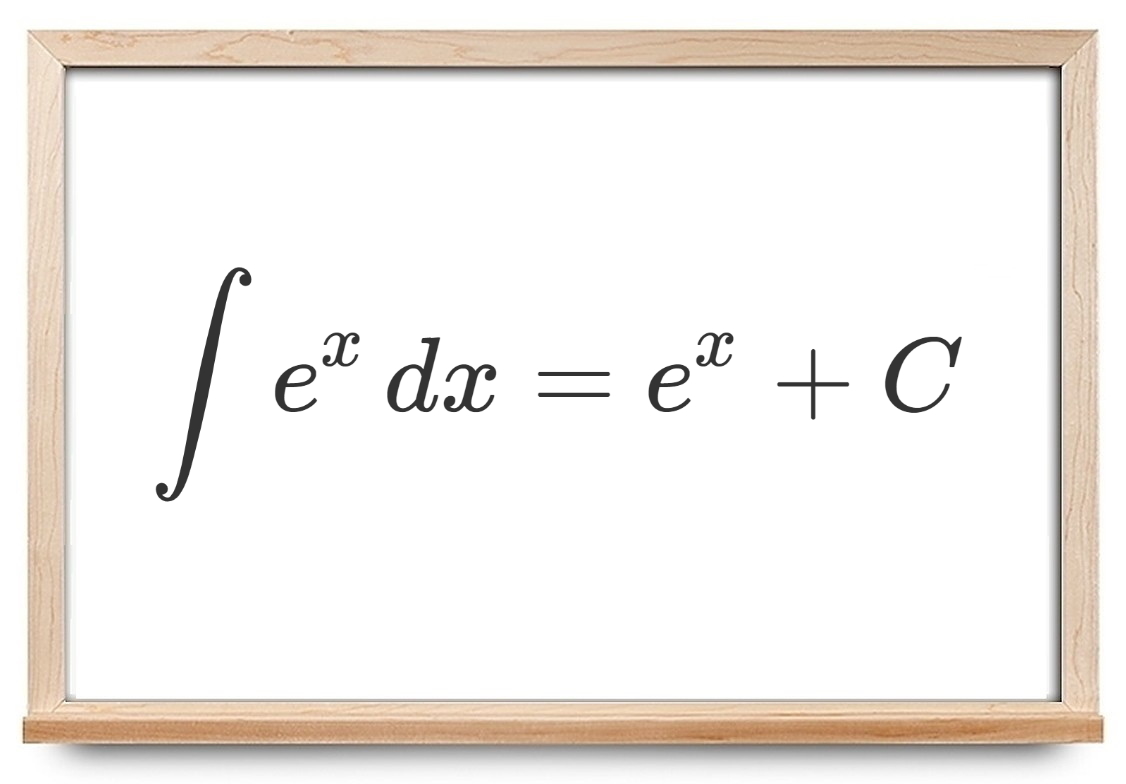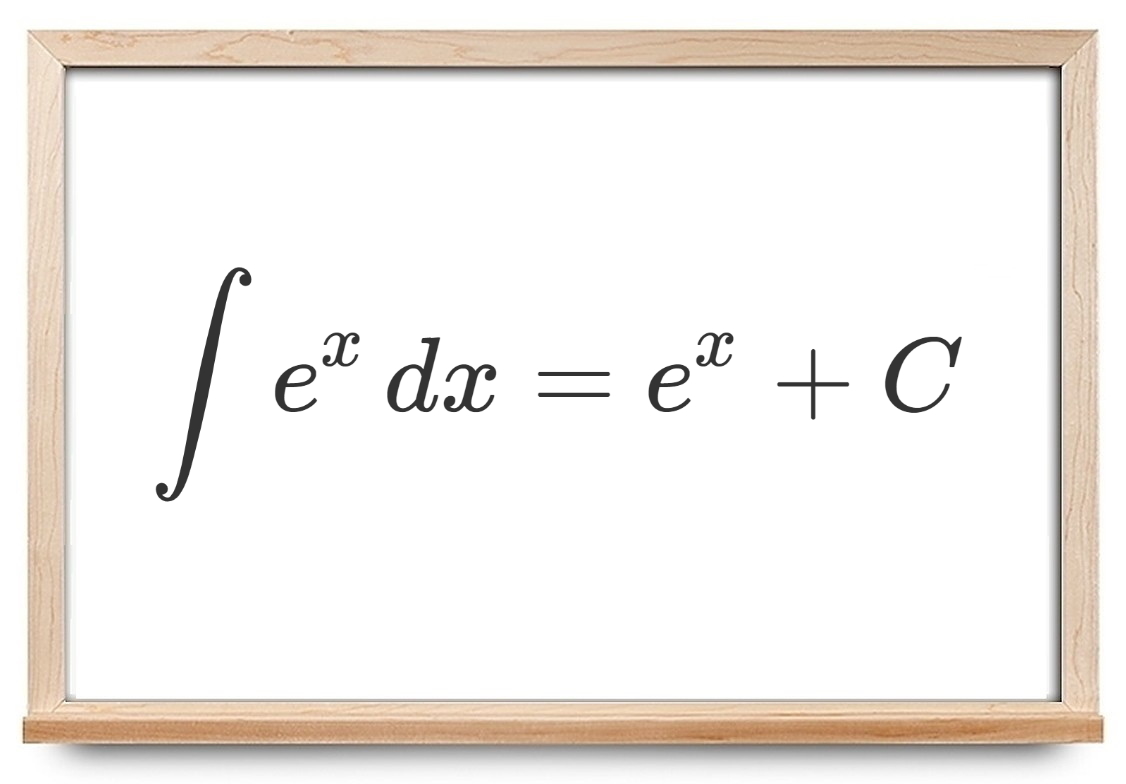در آموزشهای قبلی مجله فرادرس، با انتگرال و روشهای محاسبه آن آشنا شدیم و در مطلبی، نمونه سوالهایی از مبحث انتگرال را ارئه و حل کردیم. همچنین، در آموزشهایی به انتگرال توابع مثلثاتی ، انتگرال توابع کسری ، انتگرال توابع هیپربولیک ، انتگرالگیری جزء به جزء ، انتگرال توابع گنگ ، انتگرال رادیکالی و انتگرالگیری به روش کسرهای جزئی پرداختیم. در این آموزش با انتگرال e و روش محاسبه آن آشنا شده و مثالهایی از حل آن را بررسی میکنیم.
فرمول محاسبه انتگرال e
تابع نمایی یکی از توابع مهم است که در ریاضی بسیار با آن سر و کار داریم. مشتق و انتگرال e برابر با خودش است.
با استفاده از فرمول زیر میتوان از تابع نمایی انتگرال گرفت:
∫ e x d x = e x + C . \large \int e ^ x \, d x = e ^ x + C . ∫ e x d x = e x + C .
اگر به جای e عدد دیگری داشته باشیم، انتگرال به صورت زیر محاسبه میشود:
∫ a x d x = a x ln a + C . \large ∫ a ^ x \, d x = \dfrac { a ^ x } { \ln a } + C . ∫ a x d x = ln a a x + C .
چند فرم متداول از انتگرال e
حالت ۱: فرض کنید یک تابع نمایی به شکل زیر در انتگرال داشته باشیم:
∫ e x ( f ( x ) + f ′ ( x ) ) d x \large \int e ^ x \big ( f ( x ) + f' ( x ) \big ) \, d x ∫ e x ( f ( x ) + f ′ ( x ) ) d x
در این حالت، حاصل انتگرال برابر خواهد بود با:
e x f ( x ) + C . \large e ^ x f ( x ) + C . e x f ( x ) + C .
حالت ۲: فرض کنید انتگرال به فرم I = ∫ e a x cos ( b x + c ) \displaystyle I = \int e ^ { a x } \cos ( b x + c ) I = ∫ e a x cos ( b x + c )
I = e a x ( a cos ( b x + c ) + b sin ( b x + c ) ) a 2 + b 2 . \large I = \dfrac { e ^ { a x } \big ( a \cos ( b x + c ) + b \sin ( b x + c ) \big ) } { a ^ 2 + b ^ 2 } . I = a 2 + b 2 e a x ( a cos ( b x + c ) + b sin ( b x + c ) ) .
اثبات: انتگرال بالا را به کمک انتگرالگیری جزء به جزء حل میکنیم:
I = ∫ e a x cos ( b x + c ) d x = cos ( b x + c ) e a x a + b a ∫ e a x sin ( b x + c ) d x = cos ( b x + c ) e a x a + b a ( e a x a sin ( b x + c ) − b a ∫ e a x cos ( b x + c ) ) d x = e a x ( a cos ( b x + c ) + b sin ( b x + c ) ) a 2 − b 2 a 2 I . \large \begin {aligned} I & = \int e ^ { a x } \cos ( b x + c ) \ d x \\ & = \cos ( b x + c ) \frac { e ^ { a x } } { a } + \frac { b } { a } \int e ^ { a x } \sin ( b x + c ) \ d x\\\\ & = \cos ( b x + c ) \frac { e ^ { a x } } { a } + \frac { b } { a } \left ( \frac { e ^ { a x } } { a } \sin ( b x + c ) - \frac { b } { a } \int e ^ { a x } \cos ( b x + c ) \right ) \ d x \\\\ & = \frac { e ^ { a x } \big ( a \cos ( b x + c ) + b \sin ( b x + c ) \big ) } { a ^ 2 } - \frac { b ^ 2 } { a ^ 2 } I . \end {aligned} I = ∫ e a x cos ( b x + c ) d x = cos ( b x + c ) a e a x + a b ∫ e a x sin ( b x + c ) d x = cos ( b x + c ) a e a x + a b ( a e a x sin ( b x + c ) − a b ∫ e a x cos ( b x + c ) ) d x = a 2 e a x ( a cos ( b x + c ) + b sin ( b x + c ) ) − a 2 b 2 I .
بنابراین، خواهیم داشت:
I ( 1 + b 2 a 2 ) = e a x ( a cos ( b x + c ) + b sin ( b x + c ) ) a 2 ⇒ I = e a x ( a cos ( b x + c ) + b sin ( b x + c ) ) a 2 + b 2 . \large \begin {aligned} I \left ( 1 + \frac { b ^ 2 } { a ^ 2 } \right ) & = \frac { e ^ { a x } \big ( a \cos ( b x + c ) + b \sin ( b x + c ) \big ) } { a ^ 2 } \\ \Rightarrow I & = \frac { e ^ { a x } \big ( a \cos ( b x + c ) + b \sin ( b x + c ) \big ) } { a ^ 2 + b ^ 2 } . \end {aligned} I ( 1 + a 2 b 2 ) ⇒ I = a 2 e a x ( a cos ( b x + c ) + b sin ( b x + c ) ) = a 2 + b 2 e a x ( a cos ( b x + c ) + b sin ( b x + c ) ) .
حالت ۳: اگر انتگرال به فرم ∫ a e x + b e − x p e x + q e − x d x \displaystyle \int \frac { a e ^ x + b e ^ { - x } } { p e ^ x + q e ^ { - x } } d x ∫ p e x + q e − x a e x + b e − x d x (NUM) = α (DEN) + β d d x (DEN) \text {(NUM)} = \alpha \text {(DEN)} + \beta \frac { d } { d x } \text {(DEN)} (NUM) = α (DEN) + β d x d (DEN) NUM \text{NUM} NUM DEN \text{DEN} DEN
مثالهای حل انتگرال e
در این بخش، مثالهایی را از انتگرال e حل میکنیم.
مثال ۱ انتگرال e
انتگرال تابع e − x e^{−x} e − x
حل: از تغییر متغیر u = − x u = - x u = − x d u = − 1 d x d u = - 1 d x d u = − 1 d x d u du d u − 1 -1 − 1 − d u = d x -du=dx − d u = d x
∫ e − x d x = − ∫ e u d u = − e u + C = − e − x + C . \large ∫ e ^ { − x } \, d x = − ∫ e ^ u \, d u = − e ^ u + C = − e ^ { − x } + C . \nonumber ∫ e − x d x = − ∫ e u d u = − e u + C = − e − x + C .
مثال ۲ انتگرال e
انتگرال نامعین زیر را محاسبه کنید.
∫ ( 3 e x + 2 x ) d x \large \int ( 3 e ^ x + 2 ^ x ) \, d x ∫ ( 3 e x + 2 x ) d x
حل: حاصل این انتگرال به صورت زیر به دست میآید:
∫ ( 3 e x + 2 x ) d x = 3 ∫ e x d x + ∫ 2 x d x = 3 e x + 2 x ln 2 + C , \large \begin {aligned} \int ( 3 e ^ x + 2 ^ x ) \, d x & = 3 \int e ^ x d x + \int 2 ^ x \, d x \\ & = 3 e ^ x + \frac { 2 ^ x } { \ln 2 } + C , \end {aligned} ∫ ( 3 e x + 2 x ) d x = 3 ∫ e x d x + ∫ 2 x d x = 3 e x + ln 2 2 x + C ,
که در آن، C C C
مثال ۳ انتگرال e
انتگرال زیر را محاسبه کنید.
∫ e x + 2 d x \large \int e ^ { x + 2 } \, d x ∫ e x + 2 d x
حل: برای حل انتگرال، داریم:
∫ e x + 2 d x = ∫ e x e 2 d x = e 2 ∫ e x d x = e 2 e x + C = e x + 2 + C , \large \begin {aligned} \int e ^ { x + 2 } \, d x & = \int e ^ x e ^ 2 \, d x \\ & = e ^ 2 \int e ^ x \, d x \\ & = e ^ 2 e ^ x + C \\ & = e ^ { x + 2 } + C , \end {aligned} ∫ e x + 2 d x = ∫ e x e 2 d x = e 2 ∫ e x d x = e 2 e x + C = e x + 2 + C ,
که در آن، C C C
مثال ۴ انتگرال e
انتگرال نامعین زیر را حل کنید:
∫ e x ( sin ( x ) + cos ( x ) ) d x \large \int e ^ x \big ( \sin ( x ) + \cos ( x ) \big ) \, d x ∫ e x ( sin ( x ) + cos ( x ) ) d x
حل: این انتگرال به فرم ∫ e x ( f ( x ) + f ′ ( x ) ) d x \displaystyle \int e ^ x \big ( f ( x ) + f' ( x ) \big ) \, d x ∫ e x ( f ( x ) + f ′ ( x ) ) d x f ( x ) = sin ( x ) f ( x ) = \sin ( x ) f ( x ) = sin ( x )
e x sin ( x ) + C . \large e ^ x \sin ( x ) + C . e x sin ( x ) + C .
مثال ۵ انتگرال e
انتگرال نامعین زیر را محاسبه کنید.
∫ e 2 x cos ( 5 x + 3 ) d x \large \int e ^ { 2 x } \cos ( 5 x + 3 ) \, d x ∫ e 2 x cos ( 5 x + 3 ) d x
حل: با توجه به حالت دوم که معرفی کردیم، خواهیم داشت:
e 2 x ( 2 cos ( 5 x + 3 ) + 5 sin ( 5 x + 3 ) ) 29 + C . \large \frac { e ^ { 2 x } \big ( 2 \cos ( 5 x + 3 ) + 5 \sin ( 5 x + 3 ) \big ) } { 2 9 } + C . 29 e 2 x ( 2 cos ( 5 x + 3 ) + 5 sin ( 5 x + 3 ) ) + C .
مثال ۶ انتگرال e
انتگرال زیر را محاسبه کنید.
∫ 2 e x + 3 e − x e x − 5 e − x d x \large \int \frac { 2 e ^ x + 3 e ^ { - x } } { e ^ x - 5 e ^ { - x } } \, d x ∫ e x − 5 e − x 2 e x + 3 e − x d x
حل: با توجه به آنچه در حالت سوم گفتیم، میتوانیم تساوی زیر را بنویسیم:
2 e x + 3 e − x = α ( e x − 5 e − x ) + β ( e x + 5 e − x ) . \large 2 e ^ x + 3 e ^ { - x } = \alpha ( e ^ x - 5 e ^ { - x } ) + \beta ( e ^ x + 5 e ^ { - x } ) . 2 e x + 3 e − x = α ( e x − 5 e − x ) + β ( e x + 5 e − x ) .
با مقایسه ضرایب e x e ^ x e x e − x e ^ { - x } e − x α + β = 2 \alpha + \beta = 2 α + β = 2 α − β = − 3 5 \alpha - \beta = -\frac 35 α − β = − 5 3 α = 7 10 \alpha = \frac {7}{10} α = 10 7 β = 13 10 \beta = \frac { 13}{10} β = 10 13
∫ 2 e x + 3 e − x e x − 5 e − x d x = α ∫ d x + β ∫ e x + 5 e − x e x − 5 e − x d x . ( ∗ ) \large \int \frac { 2 e ^ x + 3 e ^ { - x } } { e ^ x - 5 e ^ { - x } } d x = \alpha \int d x + \beta \int \frac { e ^ x + 5 e ^ { -x } } { e ^ x - 5 e ^ { - x } } d x . \quad (*) ∫ e x − 5 e − x 2 e x + 3 e − x d x = α ∫ d x + β ∫ e x − 5 e − x e x + 5 e − x d x . ( ∗ )
با قرار دادن e x − 5 e − x = t e ^ x - 5 e ^ {-x } = t e x − 5 e − x = t ( e x + 5 e − x ) d x = d t (e ^ x + 5 e ^ {-x} ) d x = d t ( e x + 5 e − x ) d x = d t
( ∗ ) = 7 10 ∫ d x + 13 10 ∫ d t t = 7 x 10 + 13 10 ln ∣ t ∣ + C = 7 x 10 + 13 10 ln ∣ e x − 5 e − x ∣ + C , \large \begin {aligned} (*) & = \frac 7 { 1 0 } \int d x +\frac { 1 3 } { 1 0 } \int \frac { d t } { t } \\ & = \frac { 7 x } { 1 0 } + \frac { 1 3 } { 1 0 } \ln | t | + C \\ & = \frac { 7 x } { 1 0 } + \frac { 1 3 } { 1 0 } \ln \big | e ^ x - 5 e ^ { - x } \big | + C , \end {aligned} ( ∗ ) = 10 7 ∫ d x + 10 13 ∫ t d t = 10 7 x + 10 13 ln ∣ t ∣ + C = 10 7 x + 10 13 ln e x − 5 e − x + C ,
که در آن، C C C
مثال ۷ انتگرال e
انتگرال تابع e x 1 + e x e^x\sqrt{1+e^x} e x 1 + e x
حل: ابتدا انتگرالده را بازنویسی میکنیم:
∫ e x 1 + e x d x = ∫ e x ( 1 + e x ) 1 / 2 d x . \large ∫ e ^ x \sqrt { 1 + e ^ x } \, d x = ∫ e ^ x ( 1 + e^ x ) ^ { 1 / 2 } \, d x . ∫ e x 1 + e x d x = ∫ e x ( 1 + e x ) 1/2 d x .
با استفاده از تغییر متغیر u = 1 + e x u = 1 + e ^ x u = 1 + e x d u = e x d x d u = e ^ x d x d u = e x d x
∫ e x ( 1 + e x ) 1 / 2 d x = ∫ u 1 / 2 d u . \large ∫ e ^ x ( 1 + e ^ x ) ^ { 1 / 2 } \, d x = ∫ u ^ { 1 / 2 } \, d u . ∫ e x ( 1 + e x ) 1/2 d x = ∫ u 1/2 d u .
در نتیجه:
∫ u 1 / 2 d u = u 3 / 2 3 / 2 + C = 2 3 u 3 / 2 + C = 2 3 ( 1 + e x ) 3 / 2 + C \large ∫ u ^ { 1 / 2 } \, d u = \dfrac { u ^ { 3 / 2 } }{ 3 / 2 } + C = \dfrac { 2 } { 3 } u ^ { 3 / 2 } + C = \dfrac { 2 } { 3 } ( 1 + e ^ x ) ^ { 3 / 2 } + C ∫ u 1/2 d u = 3/2 u 3/2 + C = 3 2 u 3/2 + C = 3 2 ( 1 + e x ) 3/2 + C
مثال 8 انتگرال e
انتگرال ∫ 3 x 2 e 2 x 3 d x \displaystyle ∫ 3 x ^ 2 e ^ { 2 x^ 3 } \, d x ∫ 3 x 2 e 2 x 3 d x
حل: توان e e e u u u u = 2 x 3 u=2x^3 u = 2 x 3 d u = 6 x 2 d x du=6x^2\,dx d u = 6 x 2 d x
∫ 3 x 2 e 2 x 3 d x = 1 2 ∫ e u d u . \large ∫ 3 x ^ 2 e ^ { 2 x ^ 3 } \, d x = \frac { 1 } { 2 }∫ e ^ u \, d u . ∫ 3 x 2 e 2 x 3 d x = 2 1 ∫ e u d u .
در نتیجه، حاصل انتگرال e برابر خواهد بود با:
1 2 ∫ e u d u = 1 2 e u + C = 1 2 e 2 x 3 + C . \large \frac { 1 } { 2 } ∫ e ^ u \, d u = \frac { 1 }{ 2 } e ^ u + C = \frac { 1 } { 2 } e ^ 2 x ^ 3 + C . 2 1 ∫ e u d u = 2 1 e u + C = 2 1 e 2 x 3 + C .
مثال 9 انتگرال e
حاصل انتگرال معین زیر را به دست آورید.
∫ 0 1 x e 4 x 2 + 3 d x . \large ∫ ^ 1 _ 0 x e ^ { 4 x ^ 2 + 3 } \, d x . ∫ 0 1 x e 4 x 2 + 3 d x .
حل: از تغییر متغیر u = 4 x 3 + 3 u = 4 x ^ 3 + 3 u = 4 x 3 + 3 d u = 8 x d x d u = 8 x d x d u = 8 x d x x = 0 x = 0 x = 0 u = 3 u = 3 u = 3 x = 1 x = 1 x = 1 u = 7 u = 7 u = 7
∫ 0 1 x e 4 x 2 + 3 d x = 1 8 ∫ 3 7 e u d u = 1 8 e u ∣ 3 7 = e 7 − e 3 8 ≈ 134.568 \large \begin {align*} ∫ ^ 1 _ 0x e ^ { 4 x ^ 2 + 3 } \, d x & = \dfrac { 1 } { 8 } ∫ ^ 7 _ 3 e ^ u \, d u \\[5pt] & = \dfrac { 1 } { 8 } e ^u | ^ 7 _ 3 \\[5pt] & = \dfrac { e ^ 7 − e ^ 3 }{ 8 } \\[5pt] & ≈ 1 3 4.568 \end {align*} ∫ 0 1 x e 4 x 2 + 3 d x = 8 1 ∫ 3 7 e u d u = 8 1 e u ∣ 3 7 = 8 e 7 − e 3 ≈ 134.568
مثال 10 انتگرال e
انتگرال زیر را محاسبه کنید.
∫ 1 2 e 1 / x x 2 d x . \large ∫ ^ 2 _ 1 \dfrac { e ^ { 1 / x } } { x ^ 2 } \, d x . \nonumber ∫ 1 2 x 2 e 1/ x d x .
حل: مسئله را بازنویسی میکنیم. ابتدا e 1 x e ^ \frac 1 x e x 1 e x − 1 e ^ {x ^ {- 1 }} e x − 1 1 x 2 \frac { 1 } { x ^ 2 } x 2 1 x − 2 x ^ { - 2 } x − 2
∫ 1 2 e 1 / x x 2 d x = ∫ 1 2 e x − 1 x − 2 d x . \large ∫ ^ 2 _ 1 \dfrac { e ^ { 1 / x } }{ x ^ 2 } \, \, d x = ∫ ^ 2 _ 1 e ^ { x ^ { − 1 } } x^ { − 2 } \, d x . ∫ 1 2 x 2 e 1/ x d x = ∫ 1 2 e x − 1 x − 2 d x .
با در نظر گرفتن u = x − 1 u=x^{−1} u = x − 1 d u = − x − 2 d x du=−x^{−2}\,dx d u = − x − 2 d x
− ∫ e u d u . \large −∫e^u\,du. \nonumber − ∫ e u d u .
در ادامه، حدود انتگرالگیری را تغییر میدهیم:
u = ( 1 ) − 1 = 1 \large u=(1)^{−1}=1 \nonumber u = ( 1 ) − 1 = 1
u = ( 2 ) − 1 = 1 2 . \large u=(2)^{−1}=\dfrac{1}{2}. \nonumber u = ( 2 ) − 1 = 2 1 .
بنابراین، جواب انتگرال e برابر است با:
− ∫ 1 1 / 2 e u d u = ∫ 1 / 2 1 e u d u = e u ∣ 1 / 2 1 = e − e 1 / 2 = e − e . \large − ∫ ^ { 1 / 2 } _ 1 e ^ u \, d u = ∫ ^ 1 _ { 1 /2 } e ^ u \, d u = e ^ u \big | ^ 1 _{ 1 / 2 } = e − e ^ { 1 / 2 } = e − \sqrt { e } .\nonumber − ∫ 1 1/2 e u d u = ∫ 1/2 1 e u d u = e u 1/2 1 = e − e 1/2 = e − e .
مثال 1۱ انتگرال e
انتگرال ∫ ( 27 e 9 x + e 12 x ) 1 / 3 d x \displaystyle { \int \big ( 2 7 e ^ { 9 x } + e ^ { 1 2 x } \big ) ^ { 1 / 3 } \, d x } ∫ ( 27 e 9 x + e 12 x ) 1/3 d x
حل: ابتدا از e 9 x e ^ { 9 x } e 9 x
∫ ( 27 e 9 x + e 12 x ) 1 / 3 d x = ∫ ( 27 e 9 x + e 3 x + 9 x ) 1 / 3 d x = ∫ ( 27 e 9 x + e 3 x e 9 x ) 1 / 3 d x = ∫ ( ( e 9 x ) ( 27 + e 3 x ) ) 1 / 3 d x = ∫ ( e 9 x ) 1 / 3 ( 27 + e 3 x ) 1 / 3 d x = ∫ e ( 9 x ) ( 1 / 3 ) ( 27 + e 3 x ) 1 / 3 d x = ∫ e 3 x ( 27 + e 3 x ) 1 / 3 d x \large \begin {align*} \int \big ( 2 7 e ^ { 9 x } + e ^ { 1 2 x } \big ) ^ { 1 / 3 } \, d x & = \int \big ( 2 7 e ^ { 9 x } + e ^ { 3 x + 9 x } \big ) ^ { 1 / 3 } \, d x \\ & = { \int \big ( 2 7 e ^ { 9 x } + e ^ { 3 x} e ^ { 9 x } \big ) ^ { 1 / 3 } \, d x } \\ & = { \int \big ( \big ( e ^ { 9 x } \big ) \big ( 2 7 + e ^ { 3 x } \big ) \big ) ^ { 1 / 3 } \, d x } \\ & = { \int \big ( e ^ { 9 x } \big ) ^ { 1 / 3 } \big ( 2 7 + e ^ { 3 x } \big ) ^ { 1 / 3} \, d x } \\ & = { \int e ^ { ( 9 x ) ( 1 / 3 ) } \big ( 2 7 + e ^ { 3 x } \big ) ^ { 1 / 3 } \, d x } \\ & = { \int e ^ { 3 x } \big ( 2 7 + e ^ { 3 x } \big ) ^ { 1 / 3 } \, d x } \end {align*} ∫ ( 27 e 9 x + e 12 x ) 1/3 d x = ∫ ( 27 e 9 x + e 3 x + 9 x ) 1/3 d x = ∫ ( 27 e 9 x + e 3 x e 9 x ) 1/3 d x = ∫ ( ( e 9 x ) ( 27 + e 3 x ) ) 1/3 d x = ∫ ( e 9 x ) 1/3 ( 27 + e 3 x ) 1/3 d x = ∫ e ( 9 x ) ( 1/3 ) ( 27 + e 3 x ) 1/3 d x = ∫ e 3 x ( 27 + e 3 x ) 1/3 d x
از تغییر متغیر u = 27 + e 3 x u = 27 + e ^ { 3 x } u = 27 + e 3 x d u = 3 e 3 x d x d u = 3 e ^ { 3 x } d x d u = 3 e 3 x d x
∫ e 3 x ( 27 + e 3 x ) 1 / 3 d x = ∫ ( 27 + e 3 x ) 1 / 3 e 3 x d x = ∫ u 1 / 3 ( 1 / 3 ) d u = ( 1 / 3 ) ∫ u 1 / 3 d u = ( 1 / 3 ) u ( 1 / 3 ) + 1 ( 1 / 3 ) + 1 + C = ( 1 / 3 ) u 4 / 3 4 / 3 + C = ( 1 / 3 ) ( 3 / 4 ) ( 27 + e 3 x ) 4 / 3 + C = ( 1 / 4 ) ( 27 + e 3 x ) 4 / 3 + C \large \begin {align*} \int e ^ { 3 x } \big ( 2 7 + e ^ { 3 x } \big ) ^ { 1 / 3 } \, d x & = { \int \big ( 2 7 + e ^ { 3 x } \big ) ^ { 1 / 3 } \, e ^ { 3 x } d x } = { \int u ^ { 1 / 3 } \, ( 1 / 3 ) d u } \\ & = { ( 1 / 3 ) \int u ^ { 1 / 3 } \, d u } = { ( 1 / 3 ) { u ^ { ( 1 / 3 ) + 1 } \over ( 1 / 3 ) + 1 } } + C \\ & = { ( 1 / 3 ) { u ^ { 4 / 3 } \over 4 / 3 } } + C = { ( 1 / 3 ) ( 3 / 4 ) ( 2 7 + e ^ { 3 x } ) ^ { 4 / 3 } } + C \\ & = { ( 1 / 4 ) ( 2 7 + e ^ { 3 x } ) ^ { 4 / 3 } } + C \end {align*} ∫ e 3 x ( 27 + e 3 x ) 1/3 d x = ∫ ( 27 + e 3 x ) 1/3 e 3 x d x = ∫ u 1/3 ( 1/3 ) d u = ( 1/3 ) ∫ u 1/3 d u = ( 1/3 ) ( 1/3 ) + 1 u ( 1/3 ) + 1 + C = ( 1/3 ) 4/3 u 4/3 + C = ( 1/3 ) ( 3/4 ) ( 27 + e 3 x ) 4/3 + C = ( 1/4 ) ( 27 + e 3 x ) 4/3 + C
مثال 1۲ انتگرال e
انتگرال زیر را محاسبه کنید.
∫ 8 e x ( 3 + e x ) e 2 x + 6 e x + 1 d x \large { \int { 8 e ^ x ( 3 + e ^ x ) \over \sqrt { e ^ { 2 x } + 6 e ^ x + 1 } } \, d x } ∫ e 2 x + 6 e x + 1 8 e x ( 3 + e x ) d x
حل: از تغییر متغیر u = e 2 x + 6 e x + 1 u = e ^ { 2 x } + 6 e ^ x + 1 u = e 2 x + 6 e x + 1 d u = 2 e x ( 3 + e x ) d x d u = 2 e ^ x ( 3 + e ^ x ) d x d u = 2 e x ( 3 + e x ) d x
∫ 8 e x ( 3 + e x ) e 2 x + 6 e x + 1 d x = 8 ∫ 1 e 2 x + 6 e x + 1 e x ( 3 + e x ) d x = 8 ∫ 1 u ( 1 / 2 ) d u = 8 ( 1 / 2 ) ∫ 1 u d u = 4 ∫ 1 u d u = 4 ∫ u − 1 / 2 d u = 4 u ( − 1 / 2 ) + 1 ( − 1 / 2 ) + 1 + C = 4 u 1 / 2 1 / 2 + C = 4 ( 2 ) u 1 / 2 + C = 8 ( e 2 x + 6 e x + 1 ) 1 / 2 + C = 8 e 2 x + 6 e x + 1 + C \large \begin {align*} { \int { 8 e ^ x ( 3 + e ^ x ) \over \sqrt { e ^ { 2 x } + 6 e ^ x + 1 } } \, d x } & = \displaystyle { 8 \int { 1 \over \sqrt { e ^ { 2 x } + 6 e ^ x + 1 } } \, e ^ x ( 3 + e ^ x ) d x } \\ & = { 8 \int { 1 \over \sqrt { u } } \, ( 1 / 2) d u } = 8 ( 1 / 2 ) \int { 1 \over \sqrt { u } } \, d u \\ & = { 4 \int { 1 \over \sqrt { u } } \, d u } = { 4 \int u ^ { - 1 / 2 } \, d u } = { 4 { u ^ { ( - 1 / 2 ) + 1 } \over { ( - 1 / 2 ) + 1} } } + C \\ & = { 4 { u ^ { 1 / 2 } \over { 1 / 2 } } } + C = { 4(2) u^{1/2} } + C = { 8 ( e ^ { 2 x } + 6 e ^ x + 1 ) ^ { 1 / 2 } } + C \\ & = { 8 \sqrt { e ^ { 2 x } + 6 e ^ x + 1 } } + C \end {align*} ∫ e 2 x + 6 e x + 1 8 e x ( 3 + e x ) d x = 8 ∫ e 2 x + 6 e x + 1 1 e x ( 3 + e x ) d x = 8 ∫ u 1 ( 1/2 ) d u = 8 ( 1/2 ) ∫ u 1 d u = 4 ∫ u 1 d u = 4 ∫ u − 1/2 d u = 4 ( − 1/2 ) + 1 u ( − 1/2 ) + 1 + C = 4 1/2 u 1/2 + C = 4 ( 2 ) u 1/2 + C = 8 ( e 2 x + 6 e x + 1 ) 1/2 + C = 8 e 2 x + 6 e x + 1 + C
فهرست انتگرالهای نمایی e
در این بخش، فهرستی از انتگرالهای توابع نمایی مختلف را ارائه میکنیم.
انتگرال نامعین
انتگرالهای نامعین، توابع پادمشتق هستند و یک عدد ثابت (ثابت انتگرالگیری) به سمت راست فرمول آنها افزوده میشود. برای سادگی، ثابت انتگرالگیری را در فرمولها نیاوردهایم.
انتگرالهایی که چندجملهای دارند
∫ x e c x d x = e c x ( c x − 1 c 2 ) \large \int x e ^ { c x } \, d x = e ^ { c x } \left ( \frac { c x - 1 }{ c ^ { 2 } } \right ) ∫ x e c x d x = e c x ( c 2 c x − 1 )
∫ x 2 e c x d x = e c x ( x 2 c − 2 x c 2 + 2 c 3 ) \large \int x ^ 2 e ^ { c x } \, d x = e ^ { c x } \left ( \frac { x ^2 } {c } - \frac { 2 x } { c ^ 2 } + \frac { 2 } { c ^ 3 } \right ) ∫ x 2 e c x d x = e c x ( c x 2 − c 2 2 x + c 3 2 )
∫ x n e c x d x = 1 c x n e c x − n c ∫ x n − 1 e c x d x = ( ∂ ∂ c ) n e c x c = e c x ∑ i = 0 n ( − 1 ) i n ! ( n − i ) ! c i + 1 x n − i = e c x ∑ i = 0 n ( − 1 ) n − i n ! i ! c n − i + 1 x i \large \begin {align} \int x ^ n e ^ { c x } \, d x & = \frac { 1 } { c } x ^ n e ^ { c x } - \frac { n } { c } \int x ^ { n - 1 } e ^ { c x } \, d x \\ & = \left ( \frac { \partial } { \partial c } \right ) ^ n \frac { e ^ { c x } } { c } \\ & = e ^ { c x } \sum _ { i = 0 } ^ n ( - 1 ) ^ i \frac { n ! }{ ( n - i ) ! c ^ { i +1 } }x ^ { n - i } \\ & = e ^ { c x } \sum _ { i = 0 } ^ n ( - 1 ) ^ { n - i } \frac { n ! } { i! c ^ { n - i + 1} } x^ i \end {align} ∫ x n e c x d x = c 1 x n e c x − c n ∫ x n − 1 e c x d x = ( ∂ c ∂ ) n c e c x = e c x i = 0 ∑ n ( − 1 ) i ( n − i )! c i + 1 n ! x n − i = e c x i = 0 ∑ n ( − 1 ) n − i i ! c n − i + 1 n ! x i
∫ e c x x d x = ln ∣ x ∣ + ∑ n = 1 ∞ ( c x ) n n ⋅ n ! \large \int \frac { e ^ { c x } } { x } \, d x = \ln | x | + \sum _ { n = 1 } ^ \infty \frac { ( c x ) ^ n } { n \cdot n ! } ∫ x e c x d x = ln ∣ x ∣ + n = 1 ∑ ∞ n ⋅ n ! ( c x ) n
∫ e c x x n d x = 1 n − 1 ( − e c x x n − 1 + c ∫ e c x x n − 1 d x ) (for n ≠ 1 ) \large \int \frac { e ^ { c x } } { x ^ n } \, d x = \frac { 1 } { n- 1 } \left ( - \frac { e ^ { c x } } {x ^ { n - 1 } } + c \int \frac { e ^{ c x } } { x ^ { n - 1} } \, d x \right ) \qquad \text{(for } n \neq 1 \text {)} ∫ x n e c x d x = n − 1 1 ( − x n − 1 e c x + c ∫ x n − 1 e c x d x ) (for n = 1 )
انتگرالهایی که فقط تابع نمایی دارند
∫ f ′ ( x ) e f ( x ) d x = e f ( x ) \large \int f' ( x ) e ^ { f ( x ) } \, d x = e ^ { f ( x ) } ∫ f ′ ( x ) e f ( x ) d x = e f ( x )
∫ e c x d x = 1 c e c x \large \int e ^ { c x } \, d x = \frac { 1 } { c } e ^ { c x } ∫ e c x d x = c 1 e c x
∫ a c x d x = 1 c ⋅ ln a a c x for a > 0 , a ≠ 1 \large \int a ^ { c x } \, d x = \frac { 1 } { c \cdot \ln a } a ^ { c x } \qquad \text{ for } a > 0 , \ a \ne 1 ∫ a c x d x = c ⋅ ln a 1 a c x for a > 0 , a = 1
انتگرالهایی که توابع نمایی و مثلثاتی دارند
∫ e c x sin b x d x = e c x c 2 + b 2 ( c sin b x − b cos b x ) = e c x c 2 + b 2 sin ( b x − ϕ ) where cos ( ϕ ) = c c 2 + b 2 \large \begin {align} \int e ^ { c x } \sin b x \, d x & = \frac { e ^ { c x } } { c^ 2 + b ^ 2 } ( c \sin b x - b \cos b x ) \\ & = \frac { e ^ { c x} } { \sqrt { c ^ 2 + b ^ 2 } } \sin ( b x -\phi ) \qquad \text {where } \cos ( \phi ) = \frac { c } { \sqrt { c ^ 2 + b ^ 2 } } \end {align} ∫ e c x sin b x d x = c 2 + b 2 e c x ( c sin b x − b cos b x ) = c 2 + b 2 e c x sin ( b x − ϕ ) where cos ( ϕ ) = c 2 + b 2 c
∫ e c x cos b x d x = e c x c 2 + b 2 ( c cos b x + b sin b x ) = e c x c 2 + b 2 cos ( b x − ϕ ) where cos ( ϕ ) = c c 2 + b 2 \large \begin {align} \int e ^ { c x } \cos b x \, d x & = \frac { e ^ { c x} } { c ^ 2 + b ^2 } ( c \cos b x + b \sin b x ) \\ & = \frac { e ^ { c x } } { \sqrt { c ^ 2+ b ^ 2 } } \cos ( b x -\phi ) \qquad \text {where } \cos ( \phi ) = \frac { c } { \sqrt { c ^ 2 + b^ 2 }} \end {align} ∫ e c x cos b x d x = c 2 + b 2 e c x ( c cos b x + b sin b x ) = c 2 + b 2 e c x cos ( b x − ϕ ) where cos ( ϕ ) = c 2 + b 2 c
∫ e c x sin n x d x = e c x sin n − 1 x c 2 + n 2 ( c sin x − n cos x ) + n ( n − 1 ) c 2 + n 2 ∫ e c x sin n − 2 x d x \large \int e ^ { c x } \sin ^ n x \, d x = \frac { e ^ { c x } \sin ^ { n - 1 } x } { c ^ 2 + n ^ 2 } ( c \sin x - n \cos x) + \frac { n ( n - 1 ) } { c ^ 2 + n ^ 2 } \int e ^ { c x } \sin ^ { n - 2 } x \, d x ∫ e c x sin n x d x = c 2 + n 2 e c x sin n − 1 x ( c sin x − n cos x ) + c 2 + n 2 n ( n − 1 ) ∫ e c x sin n − 2 x d x
∫ e c x cos n x d x = e c x cos n − 1 x c 2 + n 2 ( c cos x + n sin x ) + n ( n − 1 ) c 2 + n 2 ∫ e c x cos n − 2 x d x \large \int e ^ { c x } \cos ^ n x \, d x = \frac { e ^ { c x } \cos ^ { n - 1 } x} { c ^ 2 + n ^ 2 } ( c \cos x + n \sin x ) + \frac { n ( n - 1 ) } { c ^ 2 + n ^ 2 } \int e ^ { c x } \cos ^ { n - 2 } x \, d x ∫ e c x cos n x d x = c 2 + n 2 e c x cos n − 1 x ( c cos x + n sin x ) + c 2 + n 2 n ( n − 1 ) ∫ e c x cos n − 2 x d x
انتگرالهایی که تابع خطا دارند
در فرمولهای زیر، erf \text{erf} erf Ei \text{Ei} Ei
∫ e c x ln x d x = 1 c ( e c x ln ∣ x ∣ − Ei ( c x ) ) \large \int e ^ { c x } \ln x \, d x = \frac { 1 }{ c } \left ( e ^ { c x } \ln | x | - \operatorname { E i } ( c x ) \right ) ∫ e c x ln x d x = c 1 ( e c x ln ∣ x ∣ − Ei ( c x ) )
∫ x e c x 2 d x = 1 2 c e c x 2 \large \int x e ^ { c x ^ 2 } \, d x = \frac { 1 } { 2 c } e ^ { c x ^ 2 } ∫ x e c x 2 d x = 2 c 1 e c x 2
∫ e − c x 2 d x = π 4 c erf ( c x ) \large \int e ^ { - c x ^ 2 } \, d x = \sqrt { \frac { \pi } { 4 c } } \operatorname {erf} ( \sqrt { c } x ) ∫ e − c x 2 d x = 4 c π erf ( c x )
∫ x e − c x 2 d x = − 1 2 c e − c x 2 \large \int x e ^ { - c x ^ 2 } \, d x = - \frac { 1 } { 2 c } e ^ { - c x ^ 2 } ∫ x e − c x 2 d x = − 2 c 1 e − c x 2
∫ e − x 2 x 2 d x = − e − x 2 x − π erf ( x ) \large \int \frac { e ^ {- x^ 2 } } { x ^ 2 } \, d x = -\frac { e ^ {- x ^ 2 } } {x } - \sqrt { \pi } \operatorname {erf} ( x ) ∫ x 2 e − x 2 d x = − x e − x 2 − π erf ( x )
∫ 1 σ 2 π e − 1 2 ( x − μ σ ) 2 , d x = 1 2 erf ( x − μ σ 2 ) \large \int { \frac { 1 } { \sigma \sqrt { 2 \pi } } e ^ { -\frac { 1 } { 2 } \left ( \frac { x - \mu } { \sigma } \right ) ^ 2 }} \ , d x = \frac { 1 } {2 } \operatorname {erf} \left ( \frac { x - \mu }{ \sigma \sqrt { 2 } } \right ) ∫ σ 2 π 1 e − 2 1 ( σ x − μ ) 2 , d x = 2 1 erf ( σ 2 x − μ )
سایر انتگرالها
∫ e x 2 d x = e x 2 ( ∑ j = 0 n − 1 c 2 j 1 x 2 j + 1 ) + ( 2 n − 1 ) c 2 n − 2 ∫ e x 2 x 2 n d x valid for any n > 0 , \large \int e ^ { x ^ 2 } \, d x = e ^ { x ^ 2 } \left ( \sum _ { j = 0 } ^ { n - 1 } c _ { 2 j } \frac { 1 } { x ^ { 2 j + 1 } } \right ) + ( 2 n - 1 ) c _ { 2 n- 2 } \int \frac { e ^{ x ^ 2 } } { x ^ {2 n }} \, d x \quad \text {valid for any } n > 0 , ∫ e x 2 d x = e x 2 j = 0 ∑ n − 1 c 2 j x 2 j + 1 1 + ( 2 n − 1 ) c 2 n − 2 ∫ x 2 n e x 2 d x valid for any n > 0 ,
که در آن، c 2 j = 1 ⋅ 3 ⋅ 5 ⋯ ( 2 j − 1 ) 2 j + 1 = ( 2 j ) ! j ! 2 2 j + 1 c _ { 2 j } = \frac { 1 \cdot 3 \cdot 5 \cdots ( 2 j - 1) }{ 2 ^ { j + 1 } } = \frac { ( 2 j ) ! } {j ! 2 ^ { 2 j + 1 } } c 2 j = 2 j + 1 1 ⋅ 3 ⋅ 5 ⋯ ( 2 j − 1 ) = j ! 2 2 j + 1 ( 2 j )!
∫ x x ⋅ ⋅ x ⏟ m d x = ∑ n = 0 m ( − 1 ) n ( n + 1 ) n − 1 n ! Γ ( n + 1 , − ln x ) + ∑ n = m + 1 ∞ ( − 1 ) n a m n Γ ( n + 1 , − ln x ) (for x > 0 ) \large { \int \underbrace { x ^ { x ^ { \cdot ^ { \cdot ^ { x } } } }} _ m d x = \sum _ { n = 0 } ^ m \frac { ( - 1) ^ n ( n + 1 ) ^{ n - 1 } }{ n ! } \Gamma ( n + 1 , - \ln x ) + \sum _ { n = m + 1 } ^ \infty ( - 1) ^ n a _ { m n } \Gamma ( n + 1 , - \ln x ) \qquad \text{(for }x> 0\text{)}} ∫ m x x ⋅ ⋅ x d x = n = 0 ∑ m n ! ( − 1 ) n ( n + 1 ) n − 1 Γ ( n + 1 , − ln x ) + n = m + 1 ∑ ∞ ( − 1 ) n a mn Γ ( n + 1 , − ln x ) (for x > 0 )
که در آن،
a m n = { 1 if n = 0 , 1 n ! if m = 1 , 1 n ∑ j = 1 n j a m , n − j a m − 1 , j − 1 otherwise \large a _ { m n } = \begin {cases} 1 & \text {if } n = 0, \\ \\ \dfrac { 1 } { n ! } & \text {if } m = 1 , \\ \\ \dfrac { 1 } { n } \sum _ { j = 1 } ^ { n } j a _ { m , n -j } a _ {m - 1 , j - 1 } & \text {otherwise} \end{cases} a mn = ⎩ ⎨ ⎧ 1 n ! 1 n 1 ∑ j = 1 n j a m , n − j a m − 1 , j − 1 if n = 0 , if m = 1 , otherwise
و Γ ( x , y ) \Gamma(x,y) Γ ( x , y ) تابع گاما است.
∫ 1 a e λ x + b d x = x b − 1 b λ ln ( a e λ x + b ) \large \int \frac { 1 } { a e ^ { \lambda x } + b } \, d x = \frac { x } { b } - \frac { 1 } { b \lambda } \ln \left ( a e ^ { \lambda x } + b \right ) ∫ a e λ x + b 1 d x = b x − bλ 1 ln ( a e λ x + b )
∫ e 2 λ x a e λ x + b d x = 1 a 2 λ [ a e λ x + b − b ln ( a e λ x + b ) ] \large \int \frac { e ^ { 2 \lambda x } } { a e ^ { \lambda x } + b } \, d x = \frac { 1 } { a ^ 2 \lambda } \left [ a e ^ { \lambda x } + b - b \ln\left ( a e ^ {\lambda x} + b \right) \right] ∫ a e λ x + b e 2 λ x d x = a 2 λ 1 [ a e λ x + b − b ln ( a e λ x + b ) ]
∫ a e c x − 1 b e c x − 1 d x = ( a − b ) log ( 1 − b e c x ) b c + x . \large \int \frac { a e ^ { c x} - 1 } { b e ^ { c x } - 1 } \, d x = \frac { ( a - b ) \log ( 1 - b e^ { c x} ) } { b c} + x . ∫ b e c x − 1 a e c x − 1 d x = b c ( a − b ) log ( 1 − b e c x ) + x .
انتگرالهای معین
∫ 0 1 e x ⋅ ln a + ( 1 − x ) ⋅ ln b d x = ∫ 0 1 ( a b ) x ⋅ b d x = ∫ 0 1 a x ⋅ b 1 − x d x = a − b ln a − ln b for a > 0 , b > 0 , a ≠ b \large \begin {align} \int _ 0 ^ 1 e ^ { x \cdot \ln a + ( 1 - x ) \cdot \ln b } \, dx & = \int_0^1 \left ( \frac { a } { b } \right ) ^ { x} \cdot b\,dx \\ & = \int _ 0 ^ 1 a ^ { x} \cdot b ^ { 1 - x } \, d x \\ & = \frac { a - b } { \ln a - \ln b } \qquad\text{for } a > 0,\ b > 0,\ a \neq b \end{align} ∫ 0 1 e x ⋅ l n a + ( 1 − x ) ⋅ l n b d x = ∫ 0 1 ( b a ) x ⋅ b d x = ∫ 0 1 a x ⋅ b 1 − x d x = ln a − ln b a − b for a > 0 , b > 0 , a = b
∫ 0 ∞ e − a x d x = 1 a ( Re ( a ) > 0 ) \large \int _ 0 ^ { \infty } e ^ { - a x } \, d x = \frac { 1 } { a } \quad ( \operatorname { R e } ( a ) > 0 ) ∫ 0 ∞ e − a x d x = a 1 ( Re ( a ) > 0 )
∫ 0 ∞ e − a x 2 d x = 1 2 π a ( a > 0 ) \large \int _ 0 ^ { \infty } e ^ { - a x ^ 2 } \, d x = \frac { 1 } { 2 } \sqrt { \pi \over a } \quad (a>0) ∫ 0 ∞ e − a x 2 d x = 2 1 a π ( a > 0 )
∫ − ∞ ∞ e − a x 2 d x = π a ( a > 0 ) \large \int _ { - \infty } ^ { \infty } e ^ { - a x ^ 2 } \, d x = \sqrt { \pi \over a } \quad ( a > 0 ) ∫ − ∞ ∞ e − a x 2 d x = a π ( a > 0 )
∫ − ∞ ∞ e − a x 2 + b x d x = π a e b 2 4 a ( a > 0 ) \large \int _ { - \infty } ^ { \infty } e ^ { - a x ^ 2 + b x } \, d x = \sqrt { \pi \over a } e^ { \tfrac { b ^ 2 } { 4a } } \quad(a > 0) ∫ − ∞ ∞ e − a x 2 + b x d x = a π e 4 a b 2 ( a > 0 )
∫ − ∞ ∞ e − a x 2 e − 2 b x d x = π a e b 2 a ( a > 0 ) \large \int _ { - \infty } ^ { \infty } e ^ { - a x ^ 2 } e ^ { - 2b x } \, d x = \sqrt { \frac { \pi } { a } } e ^ { \frac { b ^2 } { a } } \quad ( a > 0 ) ∫ − ∞ ∞ e − a x 2 e − 2 b x d x = a π e a b 2 ( a > 0 )
∫ − ∞ ∞ x e − a ( x − b ) 2 d x = b π a ( Re ( a ) > 0 ) \large \int _ { - \infty } ^ { \infty } x e ^ { - a ( x - b ) ^ 2 } \, d x = b \sqrt { \frac { \pi } { a } } \quad ( \operatorname { R e } ( a ) >0 ) ∫ − ∞ ∞ x e − a ( x − b ) 2 d x = b a π ( Re ( a ) > 0 )
∫ − ∞ ∞ x e − a x 2 + b x d x = π b 2 a 3 / 2 e b 2 4 a ( Re ( a ) > 0 ) \large \int _ { - \infty } ^ { \infty } x e ^ { - a x ^2 + b x } \, d x = \frac { \sqrt { \pi } b } { 2 a^ { 3 / 2 } } e ^ { \frac { b ^ 2 } { 4 a } } \quad ( \operatorname { R e } ( a ) > 0 ) ∫ − ∞ ∞ x e − a x 2 + b x d x = 2 a 3/2 π b e 4 a b 2 ( Re ( a ) > 0 )
∫ − ∞ ∞ x 2 e − a x 2 d x = 1 2 π a 3 ( a > 0 ) \large \int _ { - \infty } ^ { \infty} x ^ 2 e ^ { - a x ^ 2 } \, d x = \frac { 1 } { 2 } \sqrt { \pi \over a ^ 3 } \quad ( a > 0 ) ∫ − ∞ ∞ x 2 e − a x 2 d x = 2 1 a 3 π ( a > 0 )
∫ − ∞ ∞ x 2 e − a x 2 + b x d x = π ( 2 a + b 2 ) 4 a 5 / 2 e b 2 4 a ( Re ( a ) > 0 ) \large \int _ { - \infty } ^ { \infty } x ^ 2 e ^ { - a x ^ 2 + b x } \, d x = \frac { \sqrt { \pi } ( 2a + b ^ 2) }{ 4 a^ { 5 / 2} } e ^ { \frac { b ^ 2 }{ 4a } } \quad ( \operatorname{Re}(a)>0) ∫ − ∞ ∞ x 2 e − a x 2 + b x d x = 4 a 5/2 π ( 2 a + b 2 ) e 4 a b 2 ( Re ( a ) > 0 )
∫ − ∞ ∞ x 3 e − a x 2 + b x d x = π ( 6 a + b 2 ) b 8 a 7 / 2 e b 2 4 a ( Re ( a ) > 0 ) \large \int _ { - \infty } ^ { \infty } x ^ 3 e ^ { - a x ^ 2 + b x } \, d x = \frac { \sqrt { \pi } ( 6 a + b ^2 ) b} { 8 a ^ {7 / 2} } e ^ { \frac { b ^ 2 } { 4a } } \quad (\operatorname{Re}(a)>0) ∫ − ∞ ∞ x 3 e − a x 2 + b x d x = 8 a 7/2 π ( 6 a + b 2 ) b e 4 a b 2 ( Re ( a ) > 0 )
∫ 0 ∞ x n e − a x 2 d x = { Γ ( n + 1 2 ) 2 ( a n + 1 2 ) ( n > − 1 , a > 0 ) ( 2 k − 1 ) ! ! 2 k + 1 a k π a ( n = 2 k , k integer , a > 0 ) (!! is the double factorial) k ! 2 ( a k + 1 ) ( n = 2 k + 1 , k integer , a > 0 ) \large \int _ 0 ^ { \infty } x ^ { n } e ^ {- a x ^ 2 } \, d x = \begin {cases} \dfrac { \Gamma \left ( \frac { n + 1 } { 2 } \right ) }{ 2 \left ( a ^ \frac { n + 1 } { 2 } \right ) } & ( n >- 1 , \ a > 0) \\ \\ \dfrac { ( 2 k - 1 ) ! ! } {2 ^ { k +1 } a ^ k } \sqrt { \dfrac { \pi } { a } } & ( n = 2 k , \ k \text { integer} , \ a > 0 ) \ \text {(!! is the double factorial)} \\ \\ \dfrac{k!}{2(a^{k+1})} & (n=2k+1,\ k \text{ integer},\ a>0) \end{cases} ∫ 0 ∞ x n e − a x 2 d x = ⎩ ⎨ ⎧ 2 ( a 2 n + 1 ) Γ ( 2 n + 1 ) 2 k + 1 a k ( 2 k − 1 )!! a π 2 ( a k + 1 ) k ! ( n > − 1 , a > 0 ) ( n = 2 k , k integer , a > 0 ) (!! is the double factorial) ( n = 2 k + 1 , k integer , a > 0 )
∫ 0 ∞ x n e − a x d x = { Γ ( n + 1 ) a n + 1 ( n > − 1 , a > 0 ) n ! a n + 1 ( n = 0 , 1 , 2 , … , a > 0 ) \large \int _ 0 ^ { \infty } x ^ n e ^ { - a x } \, d x = \begin {cases} \dfrac { \Gamma ( n + 1 )} { a ^ { n+ 1 } } & ( n > - 1 , \ a > 0 ) \\ \\ \dfrac { n ! } { a ^ { n + 1 }} & (n = 0 , 1 , 2 ,\ldots,\ a>0) \end{cases} ∫ 0 ∞ x n e − a x d x = ⎩ ⎨ ⎧ a n + 1 Γ ( n + 1 ) a n + 1 n ! ( n > − 1 , a > 0 ) ( n = 0 , 1 , 2 , … , a > 0 )
∫ 0 1 x n e − a x d x = n ! a n + 1 [ 1 − e − a ∑ i = 0 n a i i ! ] \large \int _ 0 ^ { 1 } x ^n e ^ {- a x } \, d x = \frac { n ! }{ a ^{ n + 1 } } \left[ 1 - e^ { - a } \sum _ { i = 0 } ^{ n } \frac{a^i}{i!} \right] ∫ 0 1 x n e − a x d x = a n + 1 n ! 1 − e − a i = 0 ∑ n i ! a i
∫ 0 ∞ e − a x b d x = 1 b a − 1 b Γ ( 1 b ) \large \int _ 0 ^ \infty e ^ { - a x ^ b } d x = \frac { 1 } {b } \ a ^ { - \frac { 1 } { b } } \Gamma \left ( \frac { 1 } { b } \right ) ∫ 0 ∞ e − a x b d x = b 1 a − b 1 Γ ( b 1 )
∫ 0 ∞ x n e − a x b d x = 1 b a − n + 1 b Γ ( n + 1 b ) \large \int _ 0 ^ \infty x ^ n e ^ { -ax ^ b } d x = \frac { 1 } {b } \ a ^ { - \frac { n +1 } { b} } \Gamma \left ( \frac { n +1 } { b } \right ) ∫ 0 ∞ x n e − a x b d x = b 1 a − b n + 1 Γ ( b n + 1 )
∫ 0 ∞ e − a x sin b x d x = b a 2 + b 2 ( a > 0 ) \large \int_0^{\infty} e^{-ax}\sin bx\,dx = \frac{b}{a^2+b^2} \quad (a>0) ∫ 0 ∞ e − a x sin b x d x = a 2 + b 2 b ( a > 0 )
∫ 0 ∞ e − a x cos b x d x = a a 2 + b 2 ( a > 0 ) \large \int _ 0 ^ { \infty } e ^ { - a x } \cos b x \, d x = \frac { a } {a ^ 2 + b ^2 } \quad ( a > 0 ) ∫ 0 ∞ e − a x cos b x d x = a 2 + b 2 a ( a > 0 )
∫ 0 ∞ x e − a x sin b x d x = 2 a b ( a 2 + b 2 ) 2 ( a > 0 ) \large \int _ 0 ^ { \infty } x e ^ { - a x } \sin b x \, d x = \frac { 2 ab } { ( a ^ 2 + b ^2 ) ^ 2} \quad ( a > 0 ) ∫ 0 ∞ x e − a x sin b x d x = ( a 2 + b 2 ) 2 2 ab ( a > 0 )
∫ 0 ∞ x e − a x cos b x d x = a 2 − b 2 ( a 2 + b 2 ) 2 ( a > 0 ) \large \int _ 0 ^ { \infty } x e ^ { - a x } \cos b x \, d x = \frac { a ^2 - b ^ 2 }{ ( a^ 2 + b ^ 2 ) ^ 2 } \quad (a>0) ∫ 0 ∞ x e − a x cos b x d x = ( a 2 + b 2 ) 2 a 2 − b 2 ( a > 0 )
∫ 0 2 π e x cos θ d θ = 2 π I 0 ( x ) \large \int _ 0 ^ { 2 \pi } e ^ { x \cos \theta } d \theta = 2 \pi I_0(x) ∫ 0 2 π e x c o s θ d θ = 2 π I 0 ( x )
∫ 0 2 π e x cos θ + y sin θ d θ = 2 π I 0 ( x 2 + y 2 ) \large \int _ 0 ^ { 2 \pi } e ^ { x \cos \theta + y \sin \theta} d \theta = 2 \pi I _ 0 \left( \sqrt{x^2 + y^2} \right) ∫ 0 2 π e x c o s θ + y s i n θ d θ = 2 π I 0 ( x 2 + y 2 )
۱. فرمول انتگرال تابع نمایی به فرم e x e^x e x
برای انتگرال e x e^x e x
انتگرال e x e^x e x
فرمول انتگرال e x e^x e x e x e^x e x
انتگرال e x e^x e x e x e^x e x
مشاهده گزینه صحیح
فرمول انتگرال تابع نمایی به صورت e x e^x e x e x e^x e x e x e^x e x
۲. فرمول انتگرال تابع نمایی به صورت a x a^x a x e x e^x e x
برای a x a^x a x e x e^x e x
فرمول انتگرال a x a^x a x e x e^x e x
فرمول انتگرال a x a^x a x a x a^x a x e x e^x e x
انتگرال a x a^x a x a x a^x a x e x e^x e x
مشاهده گزینه صحیح
در فرمول انتگرال a x a^x a x a x a^x a x e x e^x e x e x e^x e x
۳. برای محاسبه انتگرال شامل ضرب تابع نمایی e x e^x e x
استفاده مستقیم از جدول فرمولهای ویژه انتگرالهای نمایی
استفاده از روش تغییر متغیر برای سادهسازی انتگرال
بهکاربردن انتگرال جزء به جزء برای دو تابع
تبدیل تابع به حاصل جمع کسری ساده و انتگرالگیری
مشاهده گزینه صحیح
در انتگرالهایی که ضرب تابع نمایی e x e^x e x
۴. کدام نوع انتگرال نمایی معمولا با روش تغییر متغیر حل میشود؟
انتگرال شامل ضرب تابع نمایی با یک چندجملهای باشد.
انتگرال کسری که ترکیب صورت و مخرج شامل تابع نمایی باشد.
انتگرال تابع نمایی با پایه غیر از e مانند a x a^x a x
انتگرال ترکیب تابع نمایی با توابع مثلثاتی مانند cos(ax+b) باشد.
مشاهده گزینه صحیح
وقتی انتگرال بهصورت یک کسر است که صورت یا مخرج شامل ترکیبهایی از تابع نمایی e باشد، معمولا با روش تغییر متغیر به راحتی قابل حل است. استفاده از این روش کمک میکند ساختار پیچیده ترکیبی به یک انتگرال سادهتر تبدیل شود.
۵. ویژگی خاص تابع نمایی e x e^x e x
تابع نمایی e x e^x e x
تابع e x e^x e x
انتگرال e x e^x e x
تابع نمایی e x e^x e x
مشاهده گزینه صحیح
تابع نمایی e x e^x e x
۶. برای سادهسازی انتگرالهایی که شامل عبارت e x e^{x} e x
مشاهده گزینه صحیح
برای انتگرالهایی که صورت شامل تابع نمایی e x e^{x} e x
۷. در هنگام حل انتگرال e − x e^{-x} e − x
استفاده از تغییر متغیر u = -x برای تبدیل انتگرال
تغییر متغیر به u = e x e^x e x
جایگزین کردن x با x 2 x^2 x 2
در نظر گرفتن u = x + 1 به عنوان متغیر جدید
مشاهده گزینه صحیح
اگر به جای x متغیر u = -x را قرار دهیم، مشتق x نسبت به u برابر منفی یک میشود و علامت انتگرال عوض میگردد. با این کار انتگرال e − x e^{-x} e − x e u e^{u} e u
۸. وقتی لازم باشد انتگرال یک عبارت شامل ضرب چندجملهای و تابع نمایی با پایه e را بیابید، کدام فرمول فهرست جامع مفیدتر است؟
فرمول انتگرال x^n e^{cx} برای ترکیب چندجملهای با نمایی
فرمول انتگرال e x e^x e x
فرمول انتگرال شامل تابع خطا (erf)
فرمول انتگرال ترکیبی e با توابع مثلثاتی
مشاهده گزینه صحیح
برای انتگرالگیری ترکیب چندجملهای با تابع نمایی، مانند x n e c x x^n e^{cx} x n e c x
نتیجه آزمون در مجله فرادرس
شما هیچ پاسخ صحیحی ندادید
امتیاز: ۰ از ۰
این آموزش را به خوبی یاد گرفتهاید.