انتگرال رادیکالی — به زبان ساده (+ دانلود فیلم آموزش گام به گام)

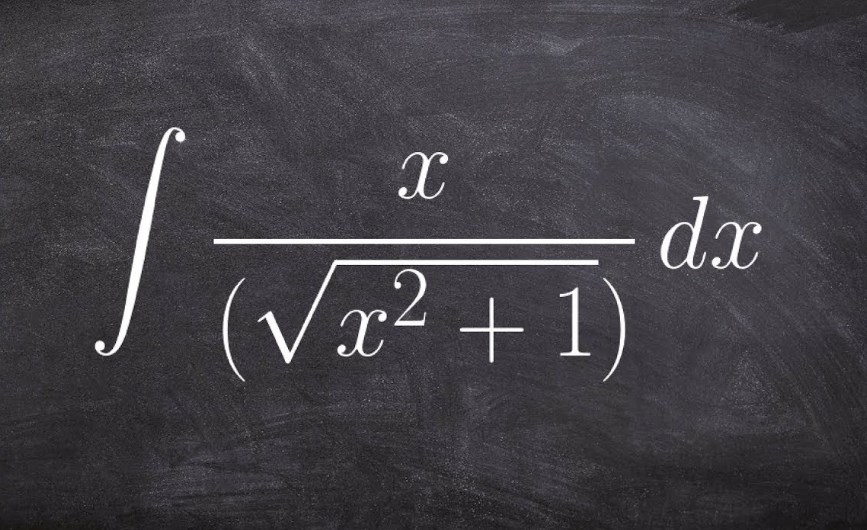
پیش‌تر در وبلاگ فرادرس در مورد مفاهیم انتگرال و نحوه محاسبه آن در توابع مختلف صحبت شد. در مطلبی مجزا نیز نحوه محاسبه انتگرال توابع مثلثاتی را توضیح دادیم. در همین راستا در این مطلب قصد داریم تا نحوه محاسبه انتگرال رادیکالی را بیان کرده و مثال‌هایی نیز از آن ارائه دهیم.

انتگرال توابع رادیکالی

در حالتی عمومی نمی‌توان رابطه‌ای واحد برای محاسبه انتگرال رادیکالی ارائه داد.

فیلم آموزش ریاضی عمومی ۱ + حل مثال و تست کنکور کارشناسی ارشد در فرادرس

کلیک کنید

در اکثر مواردی که با چنین توابعی مواجه‌اید می‌توانید حالت‌های مختلف را بررسی کرده و در صورت رخ دادن یکی از حالت‌های زیر، مسئله را حل کنید.

انتگرال شامل $$\large { \sqrt[ {n} \ ] { \left( { \frac { a x + b } { c x + d } } \right ) } } $$

برای حل انتگرال فوق باید از تغییر متغیر زیر استفاده کرد.

$$ \color {white} { { \sqrt[ { n } ] { { \frac { a x + b } { c x + d } } } }} u = { \sqrt[ {n}]{ { \frac { a x + b } { c x + d } } } } \color {white} { { \sqrt[ { n } ] { { \frac { a x + b } { c x + d } } } } } $$

مثال ۱

حاصل انتگرال زیر را بیابید.

$$ \color {white} { { \sqrt[ { n } ] { { \frac { a x + b } { c x + d } } } }} \int { \sqrt[3] { { 5 x – 1 } } d x } \color {white} { { \sqrt[ { n } ] { { \frac { a x + b } { c x + d } } } } } $$

انتگرال فوق را می‌توان با استفاده از تغییر متغیر بیان شده در بالا بدست آورد. البته توجه داشته باشید پس از نوشتن تغییر متغیر، دیفرانسیل مربوط به آن نیز باید تعریف شود. نهایتا تغییر متغیر در نظر گرفته شده و دیفرانسیل آن برابرند با:

$$ \color {white} { { \sqrt[ { n } ] { { \frac { a x + b } { c x + d } } } } } { u = {\left( { 5 x – 1 } \right)^{\frac { 1 } { 3 } } } } = { \sqrt[3]{{5x – 1 } } } \;\; \Rightarrow { 5 x – 1 = { u ^ 3 } } \;\; \Rightarrow { 5 x =
{ u ^ 3 } + 1 } \Rightarrow { x = \frac { { { u ^ 3 } + 1 } } { 5 } \;\;} \kern0pt { d x = \frac { { 3 { u ^ 2 } d u } } { 5 } } \color {white} { { \sqrt[ { n } ] { { \frac { a x + b } { c x + d } } } } } $$

در نتیجه حاصل انتگرال برابر می‌شود با:

$$\large \color {white} { { \sqrt[ { n } ] { { \frac { a x + b } { c x + d } } } } } {\int {\sqrt[3] { { 5 x – 1 } } d x } } = { \int { u \cdot \frac { { 3 { u ^ 2 } d u } } { 5 } } } = { \frac { 3 } { 5 } \int { { u ^ 3 } d u } } = { \frac { 3 }{ 5 } \cdot \frac { { { u ^ 4 } } } { 4 } + C } = { \frac { { 3 {u ^ 4 } } } { { 2 0 } } + C } = { \frac { { 3 \sqrt[3 \ \ \ ] { { \left( { { {5x – 1} } ^ 4 } \right ) } } } } { { 20 } } + C } \color {white} { { \sqrt[ { n } ] { { \frac { a x + b } { c x + d } } } } } $$

البته انتگرال فوق به‌صورت کسری نبود، از این رو حل آن نیز به‌نسبت آسان‌تر است.

مثال ۲

حاصل انتگرال زیر را بیابید.

$$ \displaystyle \int \limits ^ { \cssId {upper-bound-mathjax}{\class{placeholder}{ }}}_{\cssId{lower-bound-mathjax}{\class{placeholder}{ } } } \sqrt { \left( \dfrac{5x+2}{4x+5} \right) }\,\cssId{int-var-mathjax}{\mathrm { d } x } $$

فیلم آموزش ریاضی عمومی ۲ – مرور و حل تمرین در فرادرس

کلیک کنید

بدیهی است که باید در اولین گام خودِ تابع را به عنوان تابع $$ u $$ در نظر گرفت.

$$ u = \dfrac { \sqrt { 5 x + 2 } } { \sqrt { 4 x + 5 } } $$

در نتیجه دیفرانسیل $$ d x $$ برابر با عبارت زیر بدست می‌آید.

$$ \Rightarrow \mathrm { d } x = \dfrac { 1 } { \large \frac { 5 }{ 2 \sqrt { 4 x + 5 } \sqrt { 5 x + 2 } } – \frac { 2 \sqrt { 5 x + 2 } }{ \left ( 4 x + 5 \right ) ^ \frac { 3 } { 2 } } } \,\mathrm { d } u$$

$$ \Rightarrow \mathrm { d } x = \dfrac { 1 } { \large \frac { 5 }{ 2 \sqrt { 4 x + 5 } \sqrt { 5 x + 2 } } – \frac { 2 \sqrt { 5 x + 2 } }{ \left ( 4 x + 5 \right ) ^ \frac { 3 } { 2 } } } \,\mathrm { d } u$$

در نتیجه انتگرال فوق در قالب $$ u $$ به‌صورت زیر در می‌آید.

$$ \class{steps-node}{\cssId{steps-node-1} { 3 4}‌ } { \displaystyle\int}\dfrac { 1 } { 4 \left ( u ^ 2 \left( 4 u ^ 2 - 5 \right ) -
5 u ^ 2 \right ) + 2 5 } \,\mathrm{d}u $$

جهت حل این انتگرال باید از تکنیک‌های مربوط به حل انتگرال توابع کسری بهره برد (در مثال ۵ این روش با جزئیات بیشتر مرور شده است). در حقیقت باید تابع را به‌صورت حاصل جمع چند کسر نوشت (روش جداسازی کسر‌ها در مطلب انتگرال توابع کسری توضیح داده شده است). تابع $$ u $$ و در نتیجه آن انتگرال به‌صورت زیر در می‌آید.

$$ = \class {steps-node} { \cssId{steps-node-2}{\dfrac{1}{4{\cdot}5^\frac{3}{2} } } } { \displaystyle\int}\dfrac{1}{2u+\sqrt { 5} } \,\mathrm { d } u + \class {steps-node}{\cssId{steps-node-3}{\dfrac{1}{20 } } } { \displaystyle\int}\dfrac{1}{ \left ( 2 u + \sqrt { 5 } \right ) ^ 2 } \, \mathrm { d } u - \class{steps-node}{ \cssId{steps-node-4}{\dfrac{1}{4{\cdot} 5 ^ \frac{3}{2} } }}{ \displaystyle\int } \dfrac { 1 } { 2 u -\sqrt { 5 } } \, \mathrm {
d } u + \class {steps-node} { \cssId {steps-node-5 } { \dfrac { 1 }{20}}}{ \displaystyle\int}\dfrac { 1 } { \left(2u-\sqrt{5}\right)^2}\,\mathrm {d } u $$

برای بدست آوردن انتگرال هریک از کسر‌های فوق کافی است، عبارت‌های ارائه شده در مخرج را برابر با $$ v $$ در نظر بگیرید. در این صورت حاصل انتگرال هریک از کسر‌ها به‌راحتی بدست می‌آید. نهایتا حاصل انتگرال برابر می‌شود با:

$$\begin {align*} \class {steps-node} { \cssId {steps-node-16} { 34 } } & { \displaystyle \int } \dfrac { 1 } { 4 \left ( u ^ 2 \left ( 4 u ^ 2 - 5 \right ) - 5 u ^ 2 \right ) + 2 5 } \, \mathrm { d } u \\ & = \dfrac { 17 \ln \left ( 2 u + \sqrt { 5‌ } \right ) } { 4 { \cdot} 5 ^ \frac { 3 } { 2 } } - \dfrac { 1 7 \ln \left ( 2 u - \sqrt { 5 } \right ) }{ 4 { \cdot } 5 ^ \frac { 3 } { 2 } } - \dfrac {17} { 2 0 \left ( 2 u + \sqrt { 5 } \right ) } - \dfrac {17} { 20 \left ( 2 u - \sqrt { 5 } \right ) } \end {align*} $$

در قدم آخر به جای $$ u $$ عبارت فرض شده بر حسب $$ x $$ را در آن قرار دهید.

$$ \begin {align*} = \dfrac { 17 \ln \left ( \frac { 2 \sqrt { 5 x + 2 } }{ \sqrt { 4 x + 5 } } + \sqrt { 5 } \right ) } { 4 { \cdot} 5 ^ \frac { 3 } { 2 } } - \dfrac { 17\ln\left(\frac { 2 \sqrt { 5 x + 2 } } { \sqrt { 4 x + 5 } }-\sqrt{5}\right) } { 4 { \cdot} 5 ^ \frac { 3 } { 2 } } - \dfrac{17}{20\left(\frac{2\sqrt { 5 x + 2 } } { \sqrt{4x+5}}+\sqrt { 5 } \right)}-\dfrac {17} {20\left(\frac{2\sqrt { 5 x + 2 } } { \sqrt { 4‌ x + 5 } } -\sqrt { 5 } \right ) } \end {align*} $$

انتگرال شامل $$\large {\displaystyle {\sqrt { \left( { a ^ { 2 }- x ^ {2 } } \right ) } } } , {\displaystyle {\sqrt { \left( { a ^ { 2} + x ^ { 2 } } \right ) }} }$$ یا $$\large {\displaystyle {\sqrt { \left( { x ^ { 2} - a ^ { 2 } } \right ) } } } $$

در این موارد می‌توان از تغییر متغیر‌های مثلثاتی بهره برد. در هریک از عبارات فوق از تغییر متغیر زیر استفاده می‌کنیم.

$$\begin {align*} { \displaystyle { \sqrt { a ^ { 2 } - x ^ { 2 } } } } & \Rightarrow { \displaystyle x = a \sin ( \theta ) } \\ { \displaystyle { \sqrt { a ^ { 2 } + x ^ { 2 } } } } & \Rightarrow { \displaystyle x = a \tan ( \theta ) } \\ { \displaystyle { \sqrt { x ^ { 2 } - a ^ { 2 } } } } & \Rightarrow x=a \sec (\theta) \end {align*} $$

توجه داشته باشید که در محاسبه این نوع از انتگرال‌ها معمولا به انتگرالی به شکل کسری می‌رسید (همانند مثال ۲). در مرحله بعد باید کسر را نیز ساده کرده و نهایتا می‌توانید پاسخ انتگرال را بدست آورید.

مثال ۳

پاسخ انتگرال زیر را بدست آورید.

$$ \int { { \frac { 1 } { { { x ^ 4 } \sqrt { 9 - { x ^ 2 } } } } \, d x } } $$

فیلم آموزش ریاضی پایه دانشگاهی در فرادرس

کلیک کنید

در سوال فوق $$ \sqrt { 9 - x ^ 2 } $$ نشان می‌دهد که باید از تغییر متغیر سینوسی استفاده کنیم. بنابراین تغییر متغیر در نظر گرفته شده و دیفرانسیل معادل با آن، برابر است با:

$$ x = 3 \sin \theta \hspace {0.5in} \hspace {0.25in} d x = 3 \cos \theta \, d \theta $$

در نتیجه ترم گنگ موجود در صورت سوال را می‌توان به‌صورت زیر ساده کرد.

$$ \sqrt { 9 - { x ^ 2 } } = 3 \sqrt { 1 - { { \sin } ^ 2 } \theta } = 3 \sqrt { { { \cos } ^ 2 } \theta } = 3 \left | { \cos \theta } \right | = 3 \cos \theta $$

دلیل حذف قدر مطلق مثبت فرض کردن تمامی ترم‌ها است (این فرض اختیاری محسوب می‌شود). نهایتا شکل انتگرال را می‌توان بر حسب θ، به صورت زیر بیان کرد:

$$  \begin {align*} \int { { \frac { 1 } { { { x ^ 4 } \sqrt { 9 - { x ^ 2 } } } } \, d x } } & = \int { { \frac { 1 }{ { 8 1 { { \sin } ^ 4 } \theta \left ( { 3 \cos \theta } \right ) } } \, 3 \cos \theta \, d \theta } } \\ & = \frac { 1 } { { 8 1 } } \int { { \frac { 1 } { { { { \sin } ^ 4 } \theta } } \, d \theta } } \\ & = \frac { 1 } { { 8 1 } } \int { { { { \csc } ^ 4 } \theta \, d \theta } } \end {align*} $$

در مبحث انتگرال توابع مثلثاتی نحوه بدست آوردن توابع مثلثاتی را توضیح دادیم. به منظور محاسبه انتگرال فوق نیز می‌توان از تغییر متغیر $$ u = \cot \theta $$ استفاده کرد. بنابراین حاصل انتگرال، نهایتا به شکل زیر بدست می‌آید.

$$  \begin {align*} \int { { \frac { 1 } { { { x ^ 4 } \sqrt { 9 - { x ^ 2 } } } } \, d x } } & = \frac { 1 } { { 8 1 } } \int { { { { \csc } ^ 2 } \theta \, { { \csc } ^ 2 } \theta \, d \theta } } \\ & = \frac { 1 } { { 8 1 } } \int { { \left ( { { { \cot } ^ 2 } \theta + 1 } \right ) \, { { \csc } ^ 2 } \theta \, d \theta } } \hspace {0.5in} \Rightarrow \ \ u = \cot \theta \\ & = - \frac { 1 } { { 8 1 } } \int { { { u ^ 2 } + 1 \, d u } } \\ & = - \frac { 1 } { { 8 1 } } \left ( { \frac { 1 } { 3 } { { \cot } ^ 3 } \theta + \cot \theta } \right ) + c \end{align*} $$

به منظور محاسبه $$ \cot θ $$، بهتر است مثلثی را به‌صورت زیر در نظر گرفته و این مقدار را به‌صورت هندسی بدست آورد.

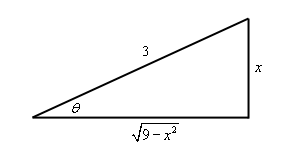
با توجه به مثلث فوق روابط زیر برقرارند.

$$  \sin \theta = \frac { x } { 3 } \hspace {0.5in} \cot \theta = \frac { { \sqrt { 9 - { x ^ 2 } } } } { x } $$

نهایتا حاصل انتگرال برابر با عبارت زیر بدست می‌آید.

$$ \begin {align*} \int { { \frac { 1 } { { { x ^ 4 } \sqrt { 9 - { x ^ 2 } } } } \, d x } } & = - \frac { 1 } { { 8 1 } } \left ( { \frac { 1 } { 3 } { { \left ( { \frac { { \sqrt { 9 - { x ^ 2 } } } } { x } } \right ) } ^ 3 } + \frac { { \sqrt { 9 - { x ^ 2 } } } } { x } } \right ) + c \\ & = - \frac { { { { \left ( { 9 - { x ^ 2 } } \right ) } ^ { \frac { 3 } { 2 } } } } }{ { 2 4 3 { x ^ 3 } } } - \frac { { \sqrt { 9 - { x ^ 2 } } } } { { 8 1 x } } + c \end {align*} $$

در برخی از موارد ممکن است، به جای $$ x $$ از عبارت $$ a x + b $$ استفاده شده باشد. در چنین مواردی در ابتدا باید عبارت زیر رادیکال را ساده‌ کرد.

مثال ۴

انتگرال زیر را با استفاده از تغییر متغیری مناسب حل کنید.

$$  \int { { \frac { x } { { \sqrt { 2 { x ^ 2 } - 4 x - 7 } } } \, d x } } $$

در ظاهر، بدیهی است که عبارت فوق یک چند جمله‌ای از درجه ۲ است. از این رو می‌توان آن را به‌ شکل مربع کامل نوشته و نهایتا از تغییر متغیر‌ مثلثاتی مناسب با آن استفاده کرد. در نتیجه عبارت زیر رادیکال را می‌توان به‌صورت زیر بیان کرد:

$$ 2 \left ( {{ x ^ 2 } - 2 x - \frac { 7 } { 2 } } \right ) = 2 \left ( { { x ^ 2 } - 2 x + 1 - 1 - \frac { 7 } { 2 } } \right ) = 2 \left ( { { { \left ( { x - 1 } \right ) } ^ 2 } - \frac { 9 } { 2 } } \right ) = 2 { \left ( { x - 1 } \right ) ^ 2 } - 9 $$

نهایتا این عبارت به شکل زیر در خواهد آمد.

$$ \sqrt { 2 { x ^ 2 } - 4 x - 7 } = \sqrt { 2 { { \left ( { x - 1 } \right ) } ^ 2 } - 9 } $$

با توجه به رابطه فوق، تغییر متغیر زیر مناسب به نظر می‌رسد.

$$ x - 1 = \frac { 3 } { { \sqrt 2 } } \sec \theta \Rightarrow \hspace {0.25in} x = 1 + \frac { 3 } { { \sqrt 2 } } \sec \theta \hspace {0.25in} , d x = \frac { 3 } { { \sqrt 2 } } \sec \theta \tan \theta \, d \theta $$

با این تغییر متغیر، عبارت رادیکالی به صورت زیر بر حسب تانژانت بدست می‌آید.

$$ \sqrt {2{x^2} - 4x - 7} = \sqrt {2{{\left( {x - 1} \right)}^2} - 9} = \sqrt {9{{\sec }^2}\theta - 9} = 3\sqrt {{{\tan }^2}\theta } = 3\left| {\tan \theta } \right| = 3\tan \theta $$

توجه داشته باشید که انتگرال‌گیری به صورت نامعین است، لذا نیازی به استفاده از قدرمطلق نیست. بنابراین نهایتا حاصل انتگرال را می‌توان به‌صورت زیر بیان کرد:

$$ \begin {align*} \int { { \frac { x } { { \sqrt { 2 { x ^ 2 } - 4 x - 7 } } } \, d x } } & = \int { { \frac{ { 1 + \frac { 3 } { { \sqrt 2 } } \sec \theta } } { { 3 \tan \theta } } \left( {\frac { 3 } { { \sqrt 2 } } \sec \theta \tan \theta } \right)\,d\theta } } \\ & = \int { { \frac { 1 } { { \sqrt 2 } } \sec \theta + \frac { 3 } { 2 } { { \sec } ^ 2 } \theta \, d \theta } } \\ & = \frac { 1 } { { \sqrt 2 } } \ln \left| {\sec \theta + \tan \theta } \right| + \frac{3}{2}\tan \theta + c\end{align*} $$

برای بدست آوردن عبارت مثلثاتی فوق، راحت‌تر آن است که در ابتدا مثلث مربوط به تغییر متغیر در نظر گرفته شده، ترسیم شود. در ادامه این مثلث ارائه شده.

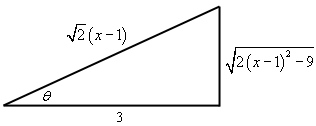
با توجه به مثلث فوق، توابع سکانت و تانژانت برابرند با:

$$ \large \sec \theta = \frac { { \sqrt 2 \left ( { x - 1 } \right ) } } { 3 } , \ \tan \theta = \frac { { \sqrt { 2 { x ^ 2 } - 4 x - 7 } } } { 3 } $$

بنابراین نهایتا حاصل انتگرال برابر می‌شود با:

$$ \int{{\frac{x}{{\sqrt {2{x^2} - 4x - 7} }}\,dx}} = \frac{1}{{\sqrt 2 }}\ln \left| {\frac{{\sqrt 2 \left( {x - 1} \right)}}{3} + \frac{{\sqrt {2{x^2} - 4x - 7} }}{3}} \right| + \frac{{\sqrt {2{x^2} - 4x - 7} }}{2} + c $$

انتگرال شامل $$ \large g ( x, { \sqrt { a x + b } } ) $$

شاید نحوه انتگرالی به شکل فوق را حدس زده‌اید. به‌منظور حل چنین انتگرالی کافی است که عبارت قرار گرفته در انتگرال رادیکالی را به عنوان یک متغیر جدید تعریف کنید. در این موارد صورت نیز باید بر حسب تغییر متغیر در نظر گرفته شده نوشته شود. بنابراین در این موارد معمولا مناسب است که از تغییر متغیر زیر استفاده شود.

$$ \large u = a x + b $$

جهت درک بهتر مثالی در ادامه ارائه شده که پیشنهاد می‌شود آن را مطالعه کنید.

مثال ۵

حاصل انتگرال $$ \displaystyle \int { { \frac { { t - 2 } } { { t - 3 \sqrt { 2 t - 4 } + 2 } } \, d t } } $$ را بدست آورید.

همان‌طور که بیان شد در این موارد بهتر است در ابتدا به فکر تغییر متغیر عبارت زیر انتگرال باشیم. در حقیقت تغییر متغیر را به‌صورت زیر در نظر می‌گیریم.

$$ u = \sqrt { 2 t - 4 } $$

با توجه به تغیdر متغیر در نظر گرفته شده، رابطه بین دیفرانسیل‌ها نیز به‌شکل زیر بدست می‌آید.

$$ t = \frac { 1 } { 2 } { u ^ 2 } + 2 \hspace {0.5in} \Rightarrow \hspace {0.5in} d t = u \, d u $$

عبارت تحت انتگرال نیز برابر است با:

$$ \begin {align*} \int { { \frac { { t - 2 } } { { t - 3 \sqrt { 2 t - 4 } + 2 } } \, d t } } & = \int { { \frac { { \frac { 1 } { 2 } { u ^ 2 } + 2 - 2 } } { { \frac { 1 } { 2 } { u ^ 2 } + 2 - 3 u + 2 } } \, \left ( u \right ) d u } } \\ & = \int { { \frac { { { u ^ 3 } } } { { {u ^ 2 } - 6 u + 8 } } \, d u } } \end {align*} $$

در بالا با انتگرالی گویا مواجه هستیم. از این رو باید آن را به‌صورت چند کسر جمع زده شده بیان کنیم. از این رو در ابتدا کسر فوق را به‌صورت زیر بازنویسی می‌کنیم.

$$ \begin {align*} \frac { { { u ^ 3 } } } { { { u ^ 2 } - 6 u + 8 } } = u + 6 + \frac { { 2 8 u - 4 8 } } { { \left ( { u - 2 } \right ) \left ( { u - 4 } \right) } } \end {align*} $$

در مرحله بعد ضرایب مجهول $$ A $$ و $$ B $$ را می‌توان به‌صورت زیر نوشت.

$$ \begin {align*} \frac { { 28 u - 48 } } { { \left ( { u - 2 } \right ) \left( { u - 4 } \right) } } = \frac { A } { { u - 2 } } + \frac { B } { { u - 4 } } \end {align*} $$

با برابر قرار دادن دو سمت عبارت فوق نیز اندازه ضرایب برابر می‌شوند با:

$$ \color {white} {28 u - 48 = A \left( { u - 4 } \right ) + B \left( { u - 2 } \right)} 28 u - 48 = A \left( { u - 4 } \right ) + B \left( { u - 2 } \right) \color {white} {28 u - 48 = A \left( { u - 4 } \right ) + B \left( { u - 2 } \right)} $$

فیلم آموزش ریاضی عمومی ۲ در فرادرس

کلیک کنید

نهایتا حاصل انتگرال نیز بر حسب تغییر متغیر در نظر گرفته شده برابر می‌شود با:

$$ \color {white} { \left( { u - 4 } \right ) + B \left( { u - 2 } \right)} \int { { \frac { { { u ^ 3 } } } { { { u ^ 2 } - 6 u + 8 } } \, d u } } = \int { { u + 6 - \frac { 4 } { { u - 2 } } + \frac { { 3 2 } } { { u - 4 } } \,d u } } = \frac { 1 } { 2 } { u ^ 2 } + 6 u - 4 \ln \left| {u - 2} \right| + 32\ln \left| {u - 4} \right| + c \color {white} {\left( { u - 4 } \right ) + B \left( { u - 2 } \right)} $$

با قرار دادن $$ u $$ در نظر گرفته شده در پاسخ بدست آمده در بالا نیز حاصل انتگرال برابر می‌شود با:

$$ \int { { \frac { { { u^ 3 } } } { { { u ^ 2 } - 6 u + 8 } } \, d u } } = \require{bbox} { { t - 2 + 6\sqrt { 2 t - 4 } - 4 \ln \left| {\sqrt { 2 t - 4 } - 2 } \right| + 32 \ln \left| {\sqrt {2t - 4} - 4} \right| + c } } $$

در این مطلب نحوه محاسبه انتگرال توابعی توضیح داده شدند که شکل آن‌ها به‌صورت رادیکالی است. در حالتی کلی معمولا می‌توان با استفاده از تغییر متغیری مثلثاتی یا تغییر متغیر بخشی از عبارت رادیکالی موجود در انتگرال، مسئله را حل کرد.

در صورت علاقه‌مندی به مباحث مرتبط در زمینه ریاضی و فیزیک، آموزش‌های زیر نیز به شما پیشنهاد می‌شوند:

• مجموعه آموزش‌های ریاضی
• مجموعه آموزش‌های دروس فیزیک
• انتگرال — به زبان ساده
• انتگرال توابع مثلثاتی — از صفر تا صد
• روش تغییر متغیر برای حل انتگرال — به زبان ساده

^^