استنباط آماری | مفاهیم اولیه و روشها – به زبان ساده
بخشی از علم آمار به بررسی جامعه آماری و خصوصیات آن اختصاص دارد. در اغلب موارد دستیابی به تک تک افراد یا اشیاء جامعه آماری میسر نیست. به همین دلیل نمونهگیری، راهکاری برای تجزیه و تحلیل ویژگیهای جامعه آماری قرار میگیرد. استنباط آماری در حقیقت نحوه تسری خصوصیات نمونه به جامعه آماری است. در این متن مفاهیم اولیه و روشهای مختلف استنباطی را مورد توجه قرار داده و معرفی میکنیم.


به منظور آشنایی بیشتر با آمار و تکنیکهای آن بهتر است نوشتارهای جامعه آماری — انواع داده و مقیاسهای آنها و آزمایش تصادفی، پیشامد و تابع احتمال را مطالعه کنید. همچنین خواندن مطالب توزیع های آماری — مجموعه مقالات جامع وبلاگ فرادرس و متغیر تصادفی، تابع احتمال و تابع توزیع احتمال نیز خالی از لطف نیست.
استنباط آماری
علم آمار را علم جمعآوری، خلاصهسازی و سازماندهی و همچنین تجزیه و تحلیل داده میشناسند. آمار را باید علم استخراج، توسعه علوم و دانش تجربی انسان در نظر گرفت که برای بیان پدیدههای تصادفی (که اغلب نیز چنین است) با استفاده از روشهای گردآوری، تنظیم، پرورش و تحلیل دادههایی به کار میرود که از طریق روشهای اندازهگیری و آزمایشگاهی بدست آمدهاند.
ابزارهای محاسباتی مدرن مانند رایانهها با استفاده از تکنیکهای آماری، علوم جدیدی همچون «یادگیری ماشینی» (Machine Learning)، و «کاوشهای ماشینی در دادهها» (Data Mining) را در امتداد و گسترش دانش گسترده و کهن آمار بوجود آوردهاند.
به این ترتیب میتوان علم آمار را شامل فنونی دانست که کار فراهم کردن دادههای کمّی و کیفی و تحلیل آنها را برمبنای احتمال میسر میسازد. هر چند این نتایج برمبنای احتمال و براساس مدلهای تصادفی ساخته میشوند ولی با اطمینان زیاد و مناسب پاسخگوی نیازهای ما هستند. به یاد داشته باشید که آن چه اهمیت دارد، این است که در گذر از آمار توصیفی به آمار استنباطی یا به عبارت دیگر از نمونه به جامعه، بحث و نقش احتمال آغاز میشود. در واقع احتمال، پل رابط بین آمار توصیفی و استنباطی به حساب میآید.
«استنباط آماری» (Inferential statistics) شاخهای از علم آمار است که در این متن جنبههای مختلف و تکنیکهای آن را معرفی خواهیم کرد.
روش های استنباط آماری
قبل از آنکه استنباط آماری انجام شود، باید دادهها و نوع آنها مشخص شده باشند. برای مثال در یک طرح تحقیقی، دادههای کیفی و کمی، پیوسته و گسسته در طرح تحقیق تعیین شده و وابستگی یا استقلال بین آنها مورد تایید قرار میگیرد.
از جنبه دیگر یکی از بخشهای مهم در آماری، قبل از اجرای استنباط آماری، جمعآوری دادهها است که بحث نمونهگیری مربوط میشود. موضوعاتی مانند خطای نمونهگیری و تعیین حجم نمونه یا «شیوه نمونهگیری» (Sampling) از مواردی است که در این بحث مطرح میشود.
به منظور کسب اطلاعات بیشتر در این زمینه میتوانید مطالب روش های نمونهگیری (Sampling) در آمار — به زبان ساده را مطالعه کنید.
مشاهدات حاصل از نمونه، در یک جامعه آماری مورد بررسی قرار میگیرند. موضوع اساسی برای بررسی نمونه و تعمیم ویژگیهای آن به جامعه آماری، براساس «تابع توزیع» (Distribution Function) تعیین میشود.
در اغلب موارد که با دادههای کمی مواجه هستیم، با استفاده از «قضیه حد مرکزی» (Central Limit Theorem) میتوان، توزیع جامعه آماری را «نرمال» (Normal Distribution) فرض کرد.
نوع آماره و توزیع به کار رفته برای اجرای استنباط، روشهای آماری را به دو بخش تقسیم کرده است. «روشهای پارامتری» (Parametric Methods) و «روشهای نارپارامتری» (Non-Parametric Methods). در ادامه به طور خلاصه ویژگیهای هر یک از روشها را بازگو خواهیم کرد.
روشهای پارامتری
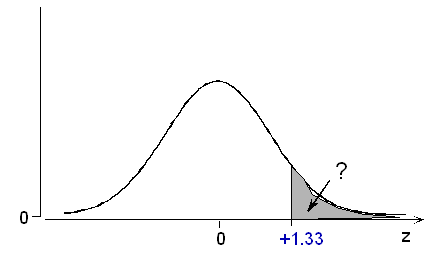
در اغلب موارد زمانی که توزیع نرمال جامعه آماری بوسیله «روشهای آزمون نرمالیتی» (Normality Test) مورد تایید قرار گرفت، تکنیکهای آماری مبتنی بر توزیع نرمال برای آماره آزمون یا فاصله اطمینان به کار گرفته میشود. همچنین «رگرسیون خطی» (Linear Regression) با تکنیک «کمترین مربعات» (OLS) نیز با نرمال بودن متغیر تصادفی خطا تکیه دارد.
در ادامه به چند روش آماری که به عنوان روشهای پارامتری شناخته میشوند، اشاره خواهیم کرد.
آزمون فرض آماری پارامتری
یکی از روشهای مطرح در استنباط آماری، آزمون فرض آماری است. در این تکنیک براساس گزارههایی که به صورت اطلاع از پارامتر جامعه یا توزیع آن نوشته میشوند، دو فرضیه میسازیم. «فرض صفر» (Null Hypothesis) و «فرض مقابل» (Alternative Hypothesis) این دو گزاره هستند.
نمونهای از فرضیات آزمون فرض آماری
فرض صفر، معمولا به گزاره یا خبری در مورد پارامتر اشاره دارد که در قبل از تحقیق آماری وجود داشته است. برای مثال میتوانیم در مورد میانگین جامعه آماری از گزاره زیر استفاده کنیم. این خبر براساس اطلاعات قدیمی و نحوه رشد دانش آموزان تهیه شده است:
«میانگین وزن دانش آموزان (جامعه آماری) برابر با ۵۳ کیلوگرم است.»
در مقابل میخواهیم نشان دهیم که استفاده از دستگاهها و بازیهای رایانهای، باعث شده است که دانش آموزان دچار اضافه وزن شوند. این خبر مبنای طرح تحقیق ما محسوب میشود. این گزاره را به صورت زیر مینویسیم:
«میانگین وزن دانش آموزان (جامعه آماری) بیشتر از ۵۳ است.»
هر دو این گزارهها، خبری را در مورد پارامتر جامعه (میانگین) ارائه کردهاند. یکی مقدار آن را دقیقا مشخص کرده و دیگری کرانی برایش در نظر گرفته است. هدف محقق آن است که به واسطه نمونهای که تهیه کرده است (با شرط انصاف) بتواند فرض صفر را رد کرده و نشان دهد که میانگین وزن، افزایش داشته است. در حقیقت، نمونه آماری، در اینجا نقش یک مثال نقض را دارد. اگر گزاره اول (فرض صفر) توسط نمونه رد شود، یک مثال نقض در رد آن ارائه شده و با کمی احتیاط، ممکن است نتیجه بگیریم که گزاره مربوط به فرض مقابل تایید میشود.
نکته: منظور از شرط انصاف، «نااریبی» (Unbiasness) و «عدم سوگیری» در نمونهها یا شرایط نمونهگیری است.
در این بین «خطای نوع اول» (Error Type I)، در آزمون فرض و تعیین «ناحیه بحرانی» (Critical Region) نقش مهمی دارند. همچنین برای تعیین «حجم نمونه» (Sample Size) برای آزمون، باید توجه مخصوص به «خطای نوع دوم» (Error Type II) داشته باشیم تا «آزمونی پرتوان» (Most Power Test) ارائه دهیم.
اگر فرض صفر را به اشتباه رد کرده باشیم، دچار خطای نوع اول شدهایم. به تفسیر دیگر میگوییم خطای نوع اول، رد فرض صفر به ناحق است. احتمال رخداد چنین پیشامدی را با نشان میدهند. باید آزمونها و ناحیه بحرانی را به شکلی برای آزمون بسازیم که میزان احتمال خطای نوع اول آن، کمینه باشد.
از طرفی خطای نوع دوم نیز به شکل رد فرض مقابل به اشتباه محسوب میشود. احتمال رخداد چنین پیشامدی نیز با نمایش داده میشود. همچنین توجه داشته باشید که توان آزمون به معنی رد فرض صفر (یا تایید فرض مقابل) به درستی است که در این حالت به شکل محاسبه میشود.
برای آشنایی بیشتر با آزمونهای آماری و نحوه اجرای آنها مطلب آزمون فرض آماری مناسب | راهنمای کاربردی را مطالعه کنید.
فاصله اطمینان پارامتری
برآورد پارامتر مجهول جامعه، یا بوسیله تکنیکهای مبتنی بر «گشتاور» (Moment) یا «بیشینه سازی تابع درستنمایی» (Maximum Likelihood) صورت میگیرد. این تکنیکها به «برآوردگرهای نقطهای» (Point Estimators) منجر میشوند. به این معنی که یک مقدار مشخص (طبق آماره) برای پارامتر جامعه، تعیین و محاسبه میگردد.
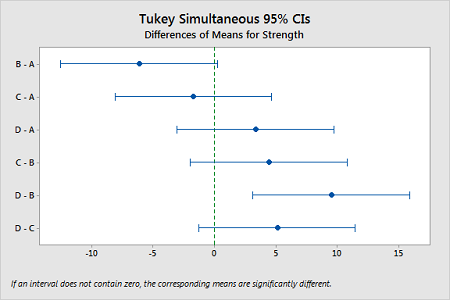
ولی اگر بخواهیم برای پارامتر، یک بازه تصادفی با درجه اطمینان معین ایجاد کنیم، فاصله اطمینان (Confidence Interval) راهحل مناسب خواهد بود. یک فاصله اطمینان به اندازه به صورت زیر نوشته میشود.
هر دو کران و «متغیرهای تصادفی» (Random Variable) هستند و در نتیجه برای آنها میتوان احتمال را محاسبه کرد. در حقیقت این احتمال براساس تابع توزیع احتمال توام و بدست میآید.
نکته: معمولا اختلاف در و در ضرایب یا مقادیر ثابت است که جنبه تصادفی ندارند. بنابراین میتوان بخش تصادفی هر دو کران را با یک توزیع تعیین کرد و در اغلب موارد احتیاجی به توزیع توام نیست.
در تصویر ۲، نمونهای از «فاصله اطمینانهای همزمان توکی» (Tukey Simultaneous Confidence Interval) را مشاهده میکنید که در تحلیل یا آنالیز واریانس به عنوان «پس آزمون» (Post-Hoc) به کار برده میشوند.
در نوشتار فاصله اطمینان و تفسیر آن — راهنمای کاربردی SPSS به طور مفصل نحوه محاسبه و توصیف فاصله اطمینان شرح داده شده است.
روشهای ناپارامتری
اگر از دنیای ایدهآل و آرمانی در آمار خارج شویم در اکثر مواقع امکان استفاده از قضیه حد مرکزی وجود ندارد. بنابراین فرض نرمال بودن و استفاده از توزیعهای مطرح آماری میسر نخواهد بود. در این حالت بدون توجه به توزیع جامعه آماری و به صرف بررسی «آمارههای ترتیبی» (Ordered Statistics) یا «آمارههای مبتنی بر شمارش» (Counting Statistics)، باید دست به قضاوت زده و استنباط آماری را اجرا کنیم. در این حالت تکنیکهای آماری را «ناپارامتری» (Non-parametric Method) یا «آزاد-توزیع» (Distribution- Free) مینامند.
نمونهای از یک آماره ترتیبی
تعیین آماره آزمون در اکثر این موارد پیچیده بوده و توزیع آنها براساس شبیهسازی در آمار یا توزیعهای گسسته مانند «توزیع دو جملهای» (Binomial Distribution) یا «چند جملهای» (Multinomial Distribution) محاسبه میشوند.
نکته: در اغلب موارد، از تقریب «توزیع کای» ۲ (-Square) برای مشخص کردن توزیع آماره آزمون استفاده میشود.
برای مثال، آزمونهای مربوط به استقلال یا نیکویی برازش برای متغیرهای تصادفی و جامعه آماری توسط توزیع کای ۲ تعیین میگردد.
آزمون فرض آماری ناپارامتری
در روشها یا تکنیکهای آمار ناپارامتری، فرض صفر و مقابل درست به مانند صورتهای پارامتری نوشته و تفسیر میشوند. خطای نوع اول و دوم نیز در اینجا مطرح است. ولی در اغلب موارد شکل توزیع آماره آزمون به سختی قابل محاسبه است. همانطور که گفته شد، در بیشتر موارد از شبیهسازی استفاده کرده و توزیع حاصل را در جدولهایی خلاصه میکنند.
این جدولها مبنایی برای اجرای آزمونهای ناپارامتری هستند. به این ترتیب برای هر یک از آزمونهای ناپارامتری، جدولی برای تعیین اندازه آزمون () و ناحیه بحرانی وجود دارد.
نکته: یکی از مواردی که باید از روشهای ناپارامتری استفاده کرد، کم بودن اندازه یا حجم نمونه است. در این موارد امکان به کارگیری قضیه حد مرکزی وجود ندارد.
چند نمونه از آزمونهای فرض آماری برای شاخص تمرکز در جامعه، آزمون «یو من ویتنی» (Mann-Whitney U) و «آزمون کروسکال والیس» (Kruskal-Wallis test) است.

فاصله اطمینان ناپارامتری
همانطور که گفته شد، توزیع آمارههای ناپارمتری، پیچیده است. به همین دلیل از روشهای دیگر مانند استفاده از تکنیکهای بازنمونهگیری برای تعیین میانگین یا واریانس (پراکندگی) آنها استفاده میکنند. به این ترتیب فاصله اطمینان حاصل نیز براساس این دو مشخصه و چندکهای توزیع که از طریق شبیهسازی بدست میآیند، ساخته میشود.
دو روش معمول برای محاسبه خطای برآوردگر یا همان واریانس یا انحراف معیار آن، استفاده از روشهای بازنمونهگیری مانند «بوت استرپ» (Bootstrap) یا «جک نایف» (Jack Knifes) است.
برآورد خطا بوسیله روشهای بوت استرپ یا جک نایف
اهمیت این دو روش در زمانی مشخص میشود که امکان محاسبه خطای برآوردگر پارامتر موجود نباشد. برای مثال در بیشتر مواقع محاسبه خطای برآوردگر برای پارامترهایی مانند صدکهای جامعه آماری به راحتی امکان پذیر نیست.
در روش جک نایف برای n مشاهده، n زیرنمونه به اندازه n-1 مشاهده به کار رفته و برای برآورد پارامتر جامعه آماری، برآوردگر محاسبه میشود. البته در هر بار نمونهگیری، دقیقا یکی از مشاهدات کنار گذاشته میشود. به این ترتیب نمیتوان آن را یک نمونهگیری با جایگذاری در نظر گرفت.
از طرفی در روش بوت استرپ، زیرنمونهها، بوسیله نمونهگیری با جایگذاری از نمونه اصلی تولید میشوند. با توجه به اینکه تعداد نمونه اصلی برابر با n است، میتوان بینهایت بار عمل زیرنمونهگیری با اندازه n را اجرا کرد.
میانگین مقادیر یافت شده برای برآوردگر، مقدار پیشبینی شده برای پارامتر در نظر گرفته شده و واریانس آنها نیز، واریانس یا خطای برآوردگر را مشخص میکند. به این ترتیب واریانس و میانگین برآوردگر بدست آمده و فاصله اطمینان را میتوان به شکلی تعیین کرد که مقدار احتمال برای کرانهای پایین و بالا (مطابق با رابطه ۱) برابر با باشد.
نکته: بحث مربوط به آمار ناپارامتری و تکنیکها در اکثر مواقع به میانه (Median) یا چندکها (Quantiles) و یا نما (Mode) بستگی دارد. در حالیکه در روشهای پارامتری، معیار مرکزی، میانگین (Mean) محسوب میشود.
رگرسیون و مدل سازی در آمار
بخشی از مسائل استنباط آماری به مدل سازی و ایجاد رابطه برگشتی یا «رگرسیون» (Regression) اختصاص داد. در این بحث به دنبال ایجاد یک تابع بین متغیر یا متغیرهای مستقل با متغیر یا متغیرهای وابسته هستیم. در زمانی که فقط یک متغیر وابسته وجود داشته باشد، مدل رگرسیونی را «چندگانه» (Multiple Regression) نامیده و در حالتی که بیش از یک متغیر وابسته وجود داشته باشد، مدل رگرسیونی «چند متغیره» (Multivariate Regression) گفته میشود.
البته شیوههایی که برای پیدا کردن ضرایب مدل رگرسیونی به کار میرود بسیار متنوع هستند. بسیاری از این مدلها در مطلب انواع روش های رگرسیونی — راهنمای جامع فهرست شدهاند.
یکی از مهمترین بخشهای نتایج حاصل از اجرای رگرسیون، ساختن «جدول تحلیل واریانس» (ANOVA) است. البته میدانید که تحلیل واریانس به منظور اجرای آزمون فرض برای میانگین بیش از دو جامعه مستقل نیز کاربرد دارد ولی در اینجا برای شناخت مناسب بودن مدل رگرسیونی، جدول آنالیز واریانس یک راهکار عالی به شمار میآید.
خلاصه و جمعبندی
در این متن به بررسی جنبههای مختلف استنباط آماری یا آمار استنباطی پرداختیم و با بعضی از مفاهیم اولیه آن آشنا شدیم. همانطور که در متن خواندید، تعمیم ویژگیهای کشف شده از نمونه به جامعه آماری از کارهای اصلی در استنباط آماری است. همچنین نحوه نمونهگیری و آزمون فرض نیز از قسمتهای اصلی علم آمار محسوب شده که در استنباط آماری کاربرد زیادی دارند. فاصله اطمینان و انواع آن نیز جنبه دیگری از استنباط آماری محسوب میشود.












