فرمول ویت (Viète’s formula) – به زبان ساده

فرمول ویت (Viète's formula)، متشکل از ضرب نامتناهی رادیکال‌های تو در تو به فرم زیر است و ثابت ریاضی $$\pi$$ را نشان می‌دهد. این فرمول به افتخار ریاضی‌دان فرانسوی، «فرانسوا ویت» (François Viète)، «ویت» نام نهاده شده است. او در قرن شانزدهم از ضرب نامتناهی برای بیان عدد π استفاده کرد. در این فرمول، فقط از عدد ۲ استفاده شده است.

فرمول ویت (Vieta's formulas) یکی از زیبا‌ترین روابط ریاضی است. این جملات ضرب شونده در واقع از مساحت یک مربع شروع می‌شوند و با هر بار ضرب شدن، مساحت 2ⁿ ضلعی منتظم به 2ⁿ⁺¹ ضلعی منتظم تبدیل می‌شود. همین کار، باعث می‌شود که نهایتا، مساحت دایره به دست بیاید که متناسب با عدد π است.

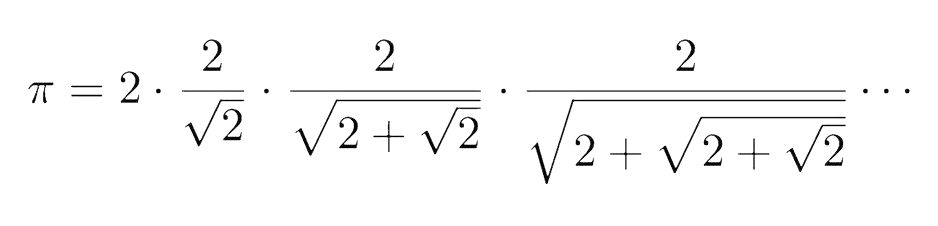
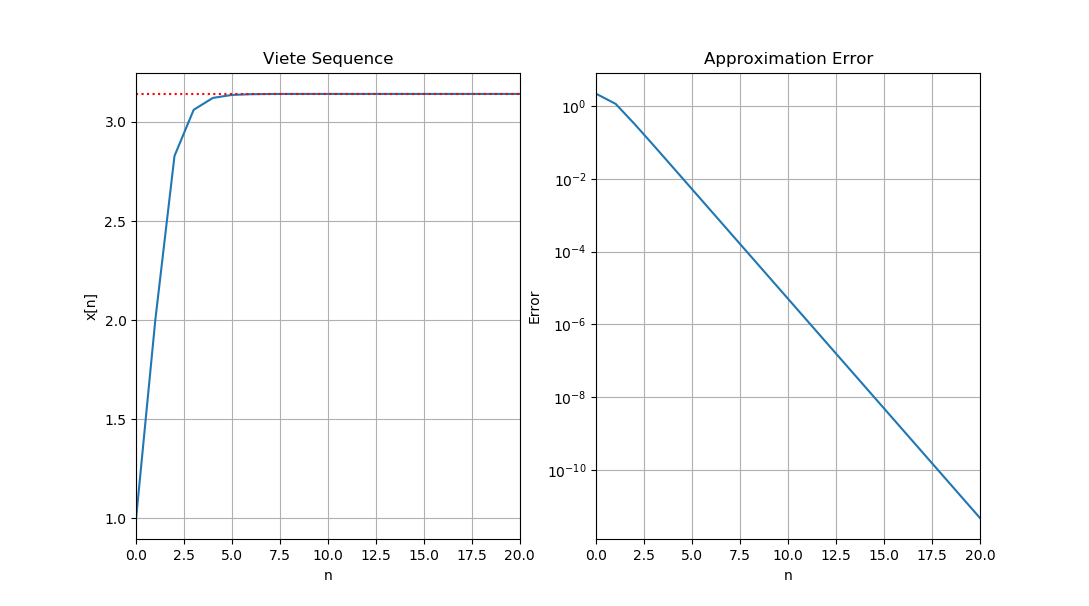
کد پایتون مربوط به شبیه‌سازی چند جمله ابتدایی سری ویت در آدامه آمده است.

1# Simulating Viete Formula for Approximation of pi
2
3import numpy as np
4import matplotlib.pyplot as plt
5
6# Number of Terms
7N = 20
8
9# Initialize Sequence
10x = np.empty(N + 1)
11x[0] = 1
12x[1] = 2
13
14# Denominator
15d = np.sqrt(2)
16
17# Calculate the Sequence Terms
18for i in range(2, N + 1):
19    x[i] = x[i-1] * 2/d
20    d = np.sqrt(2 + d)
21
22# Plot Terms
23plt.subplot(1, 2, 1)
24plt.plot(x)
25plt.plot([0, N], [np.pi, np.pi], 'r:')
26plt.title('Viete Sequence')
27plt.xlabel('n')
28plt.ylabel('x[n]')
29plt.grid(True)
30plt.xlim(0, N)
31
32# Plot Errors
33plt.subplot(1, 2, 2)
34plt.semilogy(np.pi - x)
35plt.title('Approximation Error')
36plt.xlabel('n')
37plt.ylabel('Error')
38plt.grid(True)
39plt.xlim(0, N)
40
41# Show Plots
42plt.show()

جالب است که طبق خروجی موجود در شکل زیر، در ۲۰ جمله ابتدایی، دقت این محاسبات برای تقریب عدد π، به ۱۱ رقم اعشار می‌رسد.

اگر نوشته بالا برای شما مفید بوده است، آموزش‌های زیر نیز به شما پیشنهاد می‌شوند:

• مجموعه آموزش‌های ریاضی
• مجموعه آموزش‌های ریاضی و فیزیک
• توابع نمایی و عدد e — به زبان ساده
• لگاریتم و هر آنچه باید درباره‌ آن بدانید – به زبان ساده
• بی نهایت و مفهوم آن — به زبان ساده

^^