رابطه بین بار، نیروی برشی و گشتاور خمشی — به زبان ساده

در مبحث «تحلیل نیروی برشی و گشتاور خمشی در تیرها»، با نیروی برشی و گشتاور خمشی درون تیرها، قواعد علامت‌گذاری و نحوه تحلیل آن‌ها آشنا شدیم. در این مقاله، به ارزیابی روابط بین بار، نیروی برشی و گشتاور خمشی خواهیم پرداخت. این روابط برای تحلیل نیروهای برشی و گشتاورهای خمشی موجود در کل تیر و همچنین رسم نمودارهای تنش برشی و گشتاورهای خمشی کاربردهای بسیار زیادی دارند.

مفاهیم اولیه

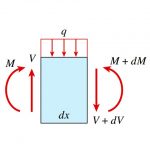
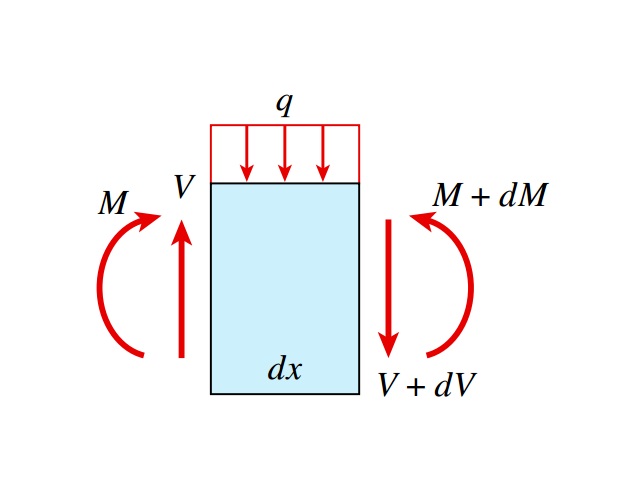
به منظور تعیین روابط بین بار، نیروی برشی و گشتاور خمشی، المان کوچکی از تیر را مطابق شکل زیر در نظر می‌گیریم. این المان بین دو مقطع عرضی با فاصله dx از یکدیگر قرار گرفته است. همان گونه که مشاهده می‌کنید، بار اعمال شده بر روی سطح بالایی المان تیر می‌تواند به صورت گسترده، متمرکز یا کوپل باشد.

به منظور علامت‌گذاری این بارها، از قواعد زیر استفاده می‌کنیم:

فیلم آموزش مقاومت مصالح – مرور و حل تست کنکور ارشد در فرادرس

کلیک کنید

• اگر جهت اعمال بارهای گسترده و متمرکز رو به پایین باشد، علامت مثبت و اگر جهت اعمال این بارها رو به بالا باشد، علامت منفی برای آن‌ها در نظر گرفته می‌شود.
• اگر جهت اعمال کوپل‌ها به صورت پادساعت‌گرد باشد، علامت مثبت و اگر جهت اعمال این کوپل‌ها به صورت ساعت‌گرد باشد، علامت منفی برای آن‌ها در نظر گرفته می‌شود.

توجه: در صورت استفاده از دیگر قواعد علامت‌گذاری، امکان تغییر علامت عبارت‌های موجود در روابط به دست آمده وجود خواهد داشت.

به طور کلی، نیروهای برشی و گشتاورهای خمشی در طول محور تیر تغییر می‌کنند. به همین دلیل، امکان متفاوت بودن مقادیر آن‌ها بر روی صفحه سمت راست المان با مقادیر روی صفحه سمت چپ وجود دارد. در بارگذاری‌های گسترده، میزان افزایش V و M بسیار کوچک است. به همین دلیل، این تغییرات به ترتیب با dV و dM نمایش داده می‌شوند. در نتیجه، برآیندهای تنش بر روی صفحه سمت راست المان برابر با V+dV و M+dM خواهند بود.

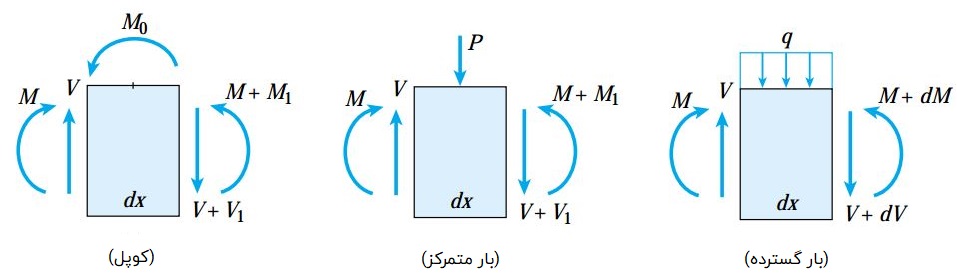
در بارگذاری‌های متمرکز یا اعمال کوپل‌ها، میزان افزایش V و M می‌تواند دارای مقدار محدود باشد. به همین دلیل، تغییرات مربوط به این نوع بارگذاری‌ها با V₁ و M₁ نمایش داده می‌شوند. در نتیجه، برآیندهای تنش بر روی صفحه سمت رایت المان برابر با V+V₁ و M+M₁ خواهند بود.

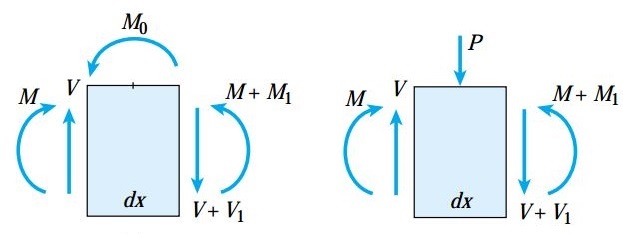
برای هر یک بارگذاری‌های معرفی شده می‌توان دو معادله تعادل نوشت. معادله اول (تعادل نیروهای موجود در راستای عمودی) به منظور تعیین رابطه بین بار و نیروی برشی و معادله دوم (تعادل گشتاورها) برای به دست آوردن رابطه بین نیروی برشی و گشتاور خمشی مورد استفاده قرار می‌گیرد.

بار گسترده

اولین نوع باری که در این مقاله مورد بررسی قرار می‌دهیم، یک بار گسترده‌ یکنواخت با شدت q است (شکل زیر). برای این حالت، در ابتدا رابطه بین شدت بار و نیروی برشی، سپس رابطه بین نیروی برشی و گشتاور خمشی را به دست می‌آوریم.

روابط بین نیروی برشی و شدت بار گسترده

با در نظر گرفتن علامت مثبت برای نیروهای رو به بالا، معادله تعادل نیروهای موجود در راستای عمودی به صورت زیر خواهد بود:

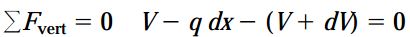
یا

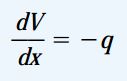
بر اساس این معادله می‌توان مشاهده کرد که نرخ تغییر نیروی برشی در هر یک از نقاط موجود بر روی محور تیر با مقدار منفی شدت بار گسترده در همان نقطه برابر است. توجه داشته باشید که اگر قاعده علامت‌گذاری بار گسترده برعکس باشد (q رو به بالا مثبت در نظر گرفته شود)، از علامت منفی معادله صرف نظر خواهد شد.

فیلم آموزش مقاومت مصالح ۱ و ۲ – مرور و حل مساله در فرادرس

کلیک کنید

با استفاده از معادله بالا می‌توان چندین رابطه کاربردی را به دست آورد. به عنوان مثال، اگر هیچ بار گسترده‌ای بر روی بخشی از تیر وجود نداشته باشد (q=0)، مقدار dV/dx برابر با صفر خواهد بود و نیروی برشی در بخش مذکور ثابت خواهد ماند. علاوه بر این، در صورت یکنواخت بودن بار گسترده بر روی بخشی از تیر (ثابت=q)، مقدار dV/dx نیز تغییر نخواهد کرد و تغییرات نیروی برشی در بخش مذکور به صورت خطی خواهد بود. برای درک بهتر رابطه معرفی شده در این بخش، شکل زیر را در نظر بگیرید. این شکل، تیر ساده‌ای را نمایش می‌دهد که در معرض یک بار گسترده متغیر قرار گرفته است. شدت این بار از مقدار صفر در نقطه A تا مقدار q₀ در نقطه B به صورت خطی تغییر می‌کند.

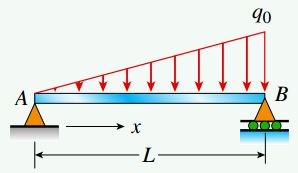
برآیند بار اعمال شده بر روی این تیر به صورت زیر محاسبه می‌شود:

به دلیل رو به پایین بودن جهت اعمال بار، شدت بار دارای علامت مثبت است. در صورت رسم نمودار جسم آزاد کل تیر، تعیین عکس‌العمل‌های تکیه‌گاهی و جمع نیروهای موجود در راستای عمودی، رابطه مورد نیاز برای محاسبه نیروی برشی به دست می‌آید (مثال 3 در مبحث تحلیل نیروی برشی و گشتاور خمشی در تیرها):

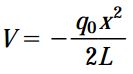
اگر از رابطه بالا مشتق بگیریم:

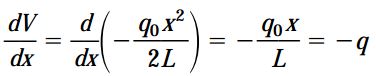
این رابطه با رابطه به دست آمده در ابتدای این بخش (dV/dx=-q) مطابقت دارد. اگر از رابطه بالا در محدوده محور طولی تیر انتگرال بگیریم، یک رابطه کاربردی برای تعیین نیروهای برشی موجود در بین دو سطح مقطع متفاوت به دست می‌آید. به این منظور، ابتدا هر دو طرف رابطه بالا را در dx ضرب می‌کنیم. سپس، در محدوده نقاط A و B بر روی محور تیر از عبارات دو طرف معادله انتگرال می‌گیریم:

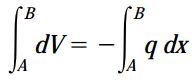
مقدار x با حرکت از روی نقطه A به سمت نقطه B افزایش می‌یابد. انتگرال سمت چپ در معادله بالا با تفاضل نیروهای برشی نقطه B و A (یعنی V_B-V_A) برابر است. انتگرال سمت راست، مساحت نمودار بارگذاری در محدوده A تا B را نمایش می‌دهد. مقدار این انتگرال با برآیند بار گسترده اعمال شده در محدوده مذکور برابری می‌کند. به این ترتیب داریم:

به عبارت دیگر، تغییرات نیروی برشی بین دو نقطه موجود بر روی محور تیر با مقدار منفی برآیند بار اعمال شده بر روی این محدوده برابر است. در صورت رو به پایین بودن جهت اعمال q، مساحت نمودار بارگذاری دارای علامت مثبت و در صورت رو به بالا بودن جهت اعمال q، این مساحت دارای علامت منفی خواهد بود.

توجه: معادلات معرفی شده در این بخش با در نظر گرفتن المانی به دست آمد که در معرض بار گسترده قرار داشت. به همین دلیل، این معادلات برای شرایط بارگذاری متمرکز به کار برده نمی‌شوند.

روابط بین نیروی برشی و گشتاور خمشی

در مرحله بعد، تعادل گشتاور المان تیر را در نظر می‌گیریم. با جمع گشتاورها حول محوری بر روی ضلع چپ المان (محوری عمود بر صفحه دربرگیرنده شکل) خواهیم داشت:

به دلیل کوچک بودن مقادیر حاصل از ضرب دو عبارت دیفرانسیلی (مانند dV*dx) نسبت به عبارات دیگر می‌توانیم از این موارد در رابطه بالا صرف نظر کنیم. با این کار به رابطه زیر خواهیم رسید:

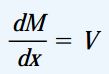
این معادله نشان می‌دهد که نرخ تغییرات گشتاور خمشی در هر یک از نقاط موجود بر روی محور تیر با نیروی برشی در همان نقطه برابر است. به عنوان مثال، اگر نیروی برشی در بخشی از تیر برابر با صفر باشد، گشتاور خمشی در آن محدوده ثابت خواهد بود. معادله بالا فقط برای نواحی تحت بار گسترده یا بدون بار کاربرد دارد. در نقطه‌ای که بار متمرکز بر روی آن اعمال می‌شود، یک تغییر ناگهانی در مقدار نیروی برشی رخ می‌دهد. در این محل، مشتق dM/dx تعریف نشده است. برای یک تیر ساده تحت بار گسترده متغیر (مانند مثال 3 در مبحث تحلیل نیروی برشی و گشتاور خمشی در تیرها)، گشتاور خمشی با استفاده از رابطه زیر به دست می‌آید:

به این ترتیب، مشتق dM/dx به صورت زیر خواهد بود:

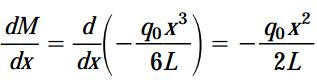
این رابطه با رابطه نیروی برشی یکسان است (dm/dx=V). اگر این رابطه را به صورت dm=Vdx بازنویسی کنیم و از دو طرف آن در محدوده A تا B انتگرال بگیریم:

انتگرال سمت چپ با تفاضل گشتاورهای خمشی موجود در نقاط B و A برابر خواهد بود (M_B-M_A). به منظور تفسیر انتگرال سمت راست، نمودار نیروی برشی (تغییرات نیروی برشی V با توجه به فاصله x) را در نظر بگیرید. این انتگرال، مساحت زیر نمودار نیروی برشی در محدوده A تا B را نمایش می‌دهد. به این ترتیب داریم:

این معادله حتی در هنگام اعمال بارهای متمرکز بر روی تیر نیز قابل استفاده است. با این وجود، اگر یک کوپل در فاصله بین A تا B بر روی تیر اعمال شود، معادله بالا کاربردی نخواهد داشت. اعمال کوپل باعث ایجاد یک تغییر ناگهانی (ناپیوستگی) در میزان گشتاور خمشی می‌شود. به همین دلیل، انتگرال سمت چپ (در معادله قبلی) بر روی این ناپیوستگی قابل محاسبه نخواهد بود.

بار متمرکز

در این بخش، یک بار متمرکز اعمال شده بر روی المان تیر را مورد بررسی قرار می‌دهیم. با در نظر گرفتن تعادل نیروها در راستای عمودی، خواهیم داشت:

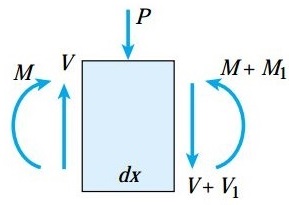
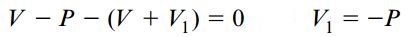
این رابطه نشان می‌دهد که در محل اعمال یک بار متمرکز، مقدار نیروی برشی با یک تغییر ناگهانی مواجهه خواهد شد. با عبور از محل اعمال این بار، میزان نیروی برشی به اندازه P کاهش می‌یابد. اگر گشتاورهای حول صفحه سمت چپ المان را با هم جمع کنیم، به معادله زیر می‌رسیم:

فیلم آموزش مقاومت مصالح – ویژه رشته عمران در فرادرس

کلیک کنید

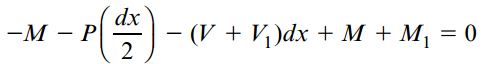
فرم ساده‌تر این معادله به صورت زیر نوشته می‌شود:

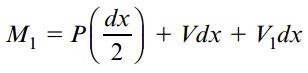
از آنجایی که طول المان مورد بررسی بسیار کوچک است (dx)، میزان افزایش گشتاور خمشی نیز کوچک خواهد بود (M₁). به همین دلیل، مقدار گشتاور خمشی با عبور از روی نقطه اعمال بار متمرکز تقریباً تغییر نمی‌کند. با وجود عدم تغییر گشتاور خمشی M در محل اعمال بار متمرکز، نرخ آن (dM/dx) در معرض یک تغییر ناگهانی قرار می‌گیرد. در ضلع سمت چپ المان، نرخ تغییرات گشتاور خمشی برابر با dM/dx=V است. این نرخ در سمت راست المان به مقدار dM/dx=V+V₁=V-P می‌رسد. در نتیجه، نرخ تغییرات گشتاور خمشی در محل اعمال بار متمرکز به اندازه آن بار (P) کاهش می‌یابد.

کوپل

در بخش آخر این مقاله، تأثیر اعمال کوپل بر روی روابط بین نیروهای برشی و گشتاورهای خمشی را مورد بررسی قرار می‌دهیم. با در نظر گرفتن تعادل نیروهای اعمال شده در راستای عمودی، V₁=0 خواهد بود. این مسئله نشان می‌دهد که مقدار نیروی برشی در محل اعمال کوپل تغییری نمی‌کند.

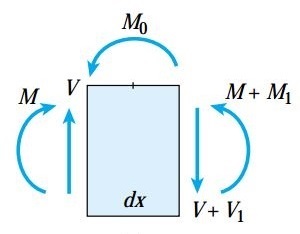
در صورت جمع کردن گشتاورهای حول صفحه سمت چپ المان به رابطه زیر می‌رسیم:

با صرف نظر کردن از عبارات دارای مقادیر دیفرانسیلی (به دلیل کوچک بودن مقدار آن‌ها)، خواهیم داشت:

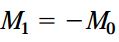
بر اساس این رابطه، با حرکت بر روی طول المان، مقدار گشتاور خمشی در محل اعمال کوپل به اندازه M₀ کاهش می‌یابد. بنابراین، گشتاور خمشی در این نقطه با یک تغییر ناگهانی مواجه خواهد شد.

^^