مفاهیم مقدماتی حسابان (بخش هفتم) — به زبان ساده

در بخش قبلی این سری مطالب آموزش مفاهیم مقدماتی حسابان با رویکردهای مختلف شهودی که برای یادگیری حسابان میتوان استفاده کرد آشنا شدیم. اینک در بخش هفتم این آموزش، یافتههای خود را تعمیم میدهیم. کار خود را با تحلیل یک الگوی ساده یعنی خط آغاز میکنیم. به معادله خط زیر توجه کنید:
بر اساس واژههای روزمره میتوان گفت که در تابع فوق باید یک ورودی به نام x وارد کرده و یک خروجی به صورت (f(x دریافت کرد. فرض کنید قصد داریم مقداری فنس خریداری کنیم. همچنین تصور کنید که هر متر طولی از فنس حدود 60 هزار تومان یعنی (f(x هزینه دارد. بدین ترتیب فنسی به طول 3 متر، هزینهای معادل 180 هزار تومان خواهد داشت.
دقت کنید که فرمول مجرد تنها شامل کمیتهای عددی است؛ اما واحدهای آن یعنی متر، تومان (هزار تومان) و غیره را شامل نمیشود. ما میتوانستیم این فرمول را چنین بنویسیم که هر متر فنس به هزینهای برابر با 600،000 ریال نیاز دارد و در این حالت به صورت زیر درمیآمد:
در این حالت محاسبات کلی باز هم بر عهده ما بود. یکی از وظایف مهم در حسابان درک x، dx و این نکته است که کمیتها اندازه دارند؛ اما واحد ندارند. بدین ترتیب میتوان مواردی مانند مساحت، حجم، تومان، ریال و غیره را حدس زد. در دنیای ریاضیات همه چیز در اعداد خلاصه میشود.
یافتن مشتق یک خط بر حسب مفاهیم مقدماتی حسابان
مشتق یک الگوی یک دنباله از قطعههایی که است به صورت تغییرات در متغیر ورودی یعنی x دریافت میکنیم این توالی مراحل به صورت زیر درک میشوند.
تصور کنید به یک فروشگاه لوازم ساختمانی میروید و گفتگوی زیر را با فروشنده دارید:
- من مقداری فنس میخواهم. هزینه آن چه قدر خواهد بود؟
- چه مقدار فنس میخواهید؟
- فکر میکنم 1 متر کافی است.
- قیمت آن 60 هزار تومان است. سؤال دیگری دارید؟
- در واقع من به 2 متر فنس نیاز دارم.
- در این صورت قیمت آن 120 هزار تومان خواهد بود. آیا سؤال دیگری دارید؟
- احتمالاً به 3 متر نیاز خواهم داشت.
- (فروشنده آهی کشیده و میگوید) بهای فنس 180 هزار تومان است. آیا سؤال دیگری دارید؟
- قیمت 4 متر چه قدر میشود؟
در این جا ما یک رابطه به صورت است که میتوان با تغییر دادن ورودی، مقدار خروجی را ملاحظه کرد. همچنین میدانیم که اگر خروجی تغییر یابد، بنابراین ورودی نیز باید تغییر یابد.
در این حالت، مشخص است که هر متر اضافی از فنس موجب میشود که بهای کل به مقدار 60 هزار تومان افزایش یابد. بنابراین میتوان نتیجه گرفت که مشتق این رابطه برابر با 60 هزار است.
البته شاید همه نتیجهگیریها به این سرعت قابل اجرا نباشد و به کمی محاسبه نیاز داشته باشد. چون همه الگوهای محاسباتی به این سادگی نیستند. در ادامه مراحل کار را توضیح دادهایم.
- خروجی فعلی را به صورت (f(x محاسبه میکنیم. در این مورد f(1)=60 است.
- به میزان dx به جلو میرویم که در این جا 1 متر است.
- مقدار جدید (f(x+dx را پیدا میکنیم. در این مثال، این مقدار برابر با f(1+1) = f(2) = 120 است.
- اختلاف را محاسبه میکنیم: f(x+dx) – f(x) = 120-60 = 60 است.
اختلاف بین گام بعدی و گام کنونی برابر با اندازه قطعه ما است. در مورد f(x)=60x داریم:
افزایش طول به اندازه dx موجب میشود که هزینه به میزان افزایش یابد. این گزاره صحیح است، اما کمی عجیب است؛ در این جا ما در مورد تغییرات کلی صحبت میکنیم. آیا بهتر نبود که این عبارت به صورت یک نسبت یعنی هزینه به ازای متر بیان میشد؟
میتوان نسبت را با چند میانبر محاسبه کرد؟
- dx = تغییر در ورودی ما
- df = تغییر حاصل از خروجی ما یعنی (f(x+dx) – f(x
- برابر با نسبت تغییرات خروجی به تغییرات ورودی است.
در این مورد رابطه زیر را داریم:
به چگونگی بیان مشتق به صورت به جای توجه کنید. بدین ترتیب مشخص میشود که چندین نسخه مختلف وجود دارد که میتوان مورد استفاده قرار داد. برای نمونه میتوان آن را به روشهای مختلفی که برای اجرای عملیات ضرب وجود دارد تشبیه کرد:
- نماد ضرب: 4 × 3 (در مدرسه ابتدایی استفاده میشود)
- نقطه: 3.4 در مدارس متوسطه استفاده میشود.
- استنباط ضرب از پرانتزها: (x+3)(x+4)
- استنباط ضرب از فاصله:
دقت کنید که هر چه نماد رابطه ظریفتر باشد؛ ما بیشتر روی رابطه بین کمیتها متمرکز میشویم؛ در سوی دیگر هر چه نماد مشخصتر باشد، بیشتر روی محاسبه متمرکز خواهیم شد.
همین مسئله در مورد نماد مشتق نیز صدق میکند:
| نماد مشتق | ذهنیت |
|---|---|
| به الگوی حاصل گام به گام فکر کنید. | |
| به نسبت واقعی تغییرات توجه کنید. |
برخی نسخهها مانند ما را به توالی گامهایی که در تغییرات الگوی اصلی وجود دارند متوجه میکنند. نمادهایی مانند ما را متوجه جزییات میکنند و به نسبت خروجی نسبت به تغییرات ورودی توجه میکنیم. یعنی هر متر اضافی چه مقدار تغییر در هزینه ایجاد میکند؟
به خاطر داشته باشید که مشتق یک توصیف کامل از همه مراحل است؛ اما میتوان آن را در نقطه مشخصی برای یافتن گام موجود نیز استفاده کنیم. برای نمونه وقتی x=3 است، هزینه یک متر فنس بیشتر چه مقدار است؟ در مثال ما پاسخ این سؤال 60 هزار تومان است.
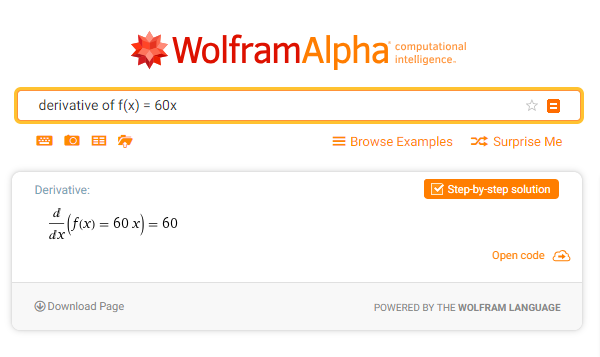
همان طور که انتظار داشتیم الگوی f(x) = 60x با افزایش x، با اندازه ثابت 60 تغییر مییابد.
یافتن انتگرال یک مقدار ثابت
اینک نوبت آن رسیده است که در سمت دیگر حرکت کنیم، یعنی با فرض وجود یک توالی، آیا میتوان اندازه الگوی اصلی را پیدا کرد؟
در سناریوی ساخت فنس این وضعیت کاملاً سرراست است. حل کردن به این معنی است که باید این سؤال پاسخ دهیم که کدام الگو تغییرات 60 برابری نسبت به تغییرات ورودی ایجاد میکند؟
همان طور که قبلاً دیدیم f(x) = 60x موجب مشتق f’(x) = 60 میشود. بنابراین با فرض f’(x) = 60 میتوانیم حدس بزنیم که تابع اصلی باید به صورت f(x)=60 باشد.
همین را با استفاده از ماشین حساب Wolfram Alpha نیز تست میکنیم:
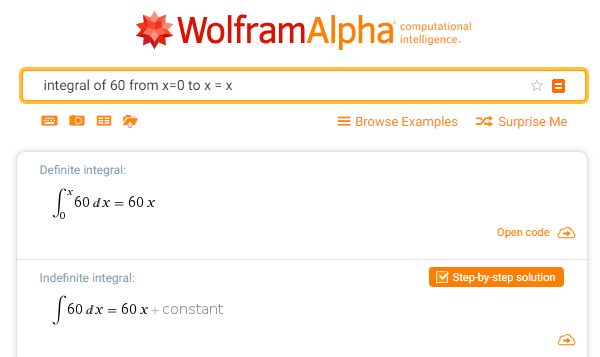
همان طور که میبینید دو پاسخ متفاوت وجود دارد که یکی پاسخ «معین» (definite) و دیگری «نامعین» (indefinite) است. دلیل این مسئله آن است که ممکن است تابعهای زیادی وجود داشته باشند که هزینه را به ازای هر متر 60 هزار تومان افزایش دهند. برای نمونه به موارد زیر توجه کنید:
- هزینه = 60 هزار تومان به ازای هر متر، یعنی f(x) = 60x
- هزینه = 60 هزار تومان + 60 هزار تومان به ازای هر متر، یعنی f(x) = 60x+60
- هزینه = 100 هزار تومان + 60 هزار تومان به ازای هر متر، یعنی f(x) = 60x+100
مواردی وجود دارند که هزینه ثابتی به ازای یک سفارش وجود دارد و هزینه فنس اضافه میشود. در واقع f’(x)=60 صرفاً اعلام میکند که هر متر فنس اضافی هزینهای برابر با 60 هزار تومان دارد؛ اما شرایط آغازین را نمیدانیم.
- انتگرال معین تجمیع یک مجموعه از قطعهها است. این بازه میتواند یک بازه عددی مانند باشد که قطعهها را از x=0 تا x=13 اندازهگیری میکند. به عبارتی 780 = 60 × 13. اگر بازه شامل یک متغیر باشد، یعنی مثلاً از 0 تا x در این صورت تجمیع یک معادله مانند 60x باید باشد.
- انتگرال نامعین فرمول واقعی را که الگوی مراحل ایجاد میکند را و نه صرفاً تجمیع بازه را توضیح میدهد. این نوع انتگرال صرفاً با استفاده از نماد انتگرال به صورت نوشته میشود. همچنان که دیدیم احتمالهای تابع اصلی باید امکان یک فاصلهگذاری ابتدایی ثابت به میزان C را داشته باشند.
نمادگذاری انتگرال میتواند سریع و سرسری باشد و از این رو سردرگمکننده خواهد بود. باید تشخیص داد که آیا به دنبال تجمیع هستیم یا تابع اصلی؟ آیا dx بر جای میماند؟ این جزییات اغلب نادیده گرفته میشوند و از این رو دانستن این که چه اتفاقی در جریان است حائز اهمیت تلقی میشود.
میتوان به سمت عقب نیز حرکت کرد
راز کوچکی که در مورد انتگرالها وجود دارد این است که لازم نیست آنها را به صورت مستقیم حل کنیم. به جای تلاش برای چسباندن قطعات مختلف در کنار هم برای یافتن مساحت، میتوانیم صرفاً مشتقهای تابعی که قبلاً دیدهایم را شناسایی کنیم.
اگر بدانیم که مشتق 60x برابر با 60 است در این صورت اگر فردی از ما بپرسد که انتگرال 60 چیست، میتوانیم بگوییم که انتگرال 60 برابر با 60x است (البته به علاوه یک C ثابت است). این وضعیت همانند بهخاطرسپاری مجذور اعداد است که در مورد محاسبه جذر نیز استفاده میشود. زمانی که فردی از ما جذر 121 را بپرسد، میتوانیم با به خاطر آوردن این واقعیت که 121 = 11 × 11 است، پاسخ او را به سرعت بدهیم.
به عنوان یک مثال دیگر میتوان باستانشناسی را تصور کرد که در حین حفاری با مشاهده دسته یک گلدان وجود آن را تشخیص دهد. این کار چگونه انجام مییابد؟ باستانشناس قطعات گلدان شکسته را کنار هم میچیند و به الگوی قطعهها نگاه میکند. سپس این باستانشناس درک میکند که مثلاً این گلدانی متعلق به سلسله مینگ در امپراطوری سوم است. او نیازی به چسباندن قطعات گلدان به هم ندارد، چون قبلاً نمونهای از آن را دیده است و این قطعه نیز مشابه نمونههای قبلی است.
اینک، ممکن است قطعاتی وجود داشته باشند که هرگز قبلاً ندیدهاید و از این رو شناسایی آنها دشوار یا ناممکن باشد. در این حالت، بهترین کاری که میتوان انجام داد این است که تکهها را کنار هم قرار دهید (احتمالاً به وسیله یک رایانه) تا بتوانید برای مثال اندازه تقریبی گلدان اولیه را تقریب بزنید. این یک روش مناسب است؛ اما به اندازه این که بدانیم گلدان قبل از خرد شدن، دقیقاً به چه شکل بوده است مفید نیست.
این بینش هرگز به طور واقعی برای ما توضیح داده نشده است، چون فرایند جمع زدن مراحل (که احتمالاً متغیر هستند) به صورت مستقیم کاری دشوار است و به خصوص زمانی که الگوی تغییر پیچیده باشد، دشوارتر میشود. بنابراین صرفاً باید مراحل شناسایی الگو از مشتقهایی که قبلاً دیدهایم را یاد بگیریم.
رسیدن به حالت بهتری از ضرب
چسباندن مراحل با اندازه یکسان تا حدودی شبیه به ضرب معمولی است. اگر بخواهیم 3 مرحله (0 تا 1، 1 تا 2 و 2 تا 3) را با اندازه 2 داشته باشیم، میتوانیم به صورت زیر بنویسیم:
این نیز یک روش جالب برای بیان این واقعیت است که مجموع 3 مرحله 2 واحدی برابر با 6 خواهد بود. در واقع ما از رویکرد تایملپس که در بخش نخست این سری مطالب آموزش حسابان معرفی کردیم برای یک دنباله از تغییرهای مساوی استفاده کردهایم.
اینک فرض کنید فردی از شما میخواهد که جمع زیر را انجام دهید:
2 + 2 + 2 + 2 + 2 + 2 + 2 + 2 + 2 + 2 + 2 + 2 + 2
ممکن است بگویید میتوان جمع فوق را به روشی ساده و مثلاً مانند زیر نوشت:
ایجاد قواعد مجرد
آیا ایدهای در مورد شیوه رفتار تابعهای خطی دارید؟ میتوانیم چندین قاعده مجرد مانند قواعد محاسبه جبری برای خود داشته باشیم. اگر بدانیم که خروجی ما نسخه مقیاس یافتهای از ورودی f(x) = ax است، مشتق (الگوی تغییر) به صورت زیر خواهد بود:
و انتگرال (الگوی تجمیع) چنین است:
این بدان معنی است که نسبت هر گام خروجی به هر گام ورودی مقدار ثابت a است. اینک که گلدان شکسته را در دست داریم میتوانیم روبه سمت عقب حرکت کنیم و با تجمیع مراحل با اندازه a به الگویی به شکل a.x (البته به علاوه C) برسیم.
دقت کنید که ما را نوشتهایم و را ننوشتهایم، زیرا میخواهیم روی a تمرکز کنیم و نه جزییاتی مانند عرض مرحله (dx). بخشی از حسابان این است که بدانیم باید چه مقدار از جزییات را افشا کنیم.
نکته آخری که باید اشاره کرد این است که خروجی ما به طور کامل به ورودی واکنش نشان نمیدهد. در واقع شما همیشه مقدار ثابت 2 را دارید و مهم نیست که چه مقدار خرید کنید و حتی اگر خرید نکنید هم این مقدار ثابت است. در این حالت مراحل مختلف برابر با ثابت 0 است:
به بیان دیگر هیچ تفاوتی در اندازهگیری قبل و بعد وجود ندارد. اینک یک الگویی داریم که میتواند قطعهای با اندازه صفر داشته باشد و با این حال برای لحظهای پابرجا باشد. این وضعیت اشکالی ندارد؛ اما اگر همه قطعهها برابر با صفر باشند، این بدان معنی است که الگوی ما هرگز تغییر نمییابد. در بخش بعدی در مورد این مباحث بیشتر توضیح خواهیم داد.
اگر این مطلب برای شما مفید بوده است، آموزشهای زیر نیز به شما پیشنهاد میشوند:
- مجموعه آموزشهای ریاضیات
- آموزش جامع حساب دیفرانسیل و انتگرال پیش دانشگاهی
- مجموعه آموزشهای دروس رسمی دبیرستان و پیش دانشگاهی
- آموزش مشتق در ریاضیات عمومی ۱
- انتگرال — به زبان ساده
- انتگرال و روش های محاسبه — به زبان ساده
==












