الگوریتم اپریوری (Apriori) به همراه کد پیاده‌سازی در پایتون — کاوش قواعد وابستگی در داده‌کاوی

الگوریتم اپریوری (Apriori) بر این اصل بنا شده که اگر یک مجموعه اقلام (itemset) مکرر است، پس همه زیرمجموعه‌های آن نیز مکرر هستند. این بدین معنا است که اگر {0,1} مکرر باشد، پس {0} و {1} نیز مکرر هستند. بالعکس این قاعده نیز صادق است، یعنی اگر یک مجموعه اقلام مکرر نباشد، زیرمجموعه‌های آن نیز مکرر نیستند. با توجه به توضیحات بالا، برای یافتن یک مجموعه قواعد وابستگی، ابتدا باید مجموعه اقلام مکرر را پیدا کرد. برای حل این مساله، نیاز به کار با نوع داده‌های عددی و اسمی (دسته‌ای) است.

تحلیل وابستگی

جست‌و‌جو به دنبال روابط در پایگاه داده‌های بزرگ با عنوان تحلیل وابستگی یا کاوش قواعد وابستگی (association rule mining) شناخته شده است. مساله آن است که کشف ترکیب‌های گوناگون از اقلام می‌تواند کاری زمان‌بر و چه بسا از لحاظ توان پردازشی غیر ممکن باشد. این ترکیب‌ها به دو شکل ممکن است به وقوع بپیوندند. این دو فرم عبارتند از اقلام مکرر و قواعد وابستگی. مجموعه اقلام مکرر مجموعه‌ای از آیتم‌ها هستند که مکررا با یکدیگر به وقوع می‌پیوندند. دومین راه برای مشاهده روابط جالب بین آیتم‌ها، قواعد وابستگی است. قواعد وابستگی، ارتباطات قدرتمند بین آیتم‌ها را تبیین می‌کنند.

فیلم آموزش اصول و روش های متن کاوی Text Mining در فرادرس

کلیک کنید

با استفاده از کاوش مجموعه اقلام مکرر، خرده‌فروشان قادر به کسب درک بهتر از مشتریان خود هستند. دیگر مثال از کاربردهای قواعد وابستگی، موتورهای جست‌و‌جو است. برای کاوش مجموعه اقلام مکرر و کشف قواعد وابستگی، از پشتیبان و اطمینان به عنوان راهکارهایی استفاده می‌شود که با بهره‌گیری از آن‌ها می‌توان تحلیل وابستگی را کمّی کرد.

پشتیبان یک مجموعه اقلام، به عنوان درصدی از مجموعه داده که شامل آن مجموعه اقلام است تعریف شده. اطمینان برای قاعده P ➞ H به صورت (support(P | H) / support(P تعریف شده است. در پایتون، علامت «|» برای اتحاد مجموعه‌ها به کار می‌رود، این در حالیست که نماد ریاضی اتحاد مجموعه‌ها «U» است. P | H یعنی (اتحاد P و H) شامل همه آیتم‌های موجود در مجموعه P یا H است.

رویکرد عمومی به الگوریتم اپریوری (Apriori)

1. گردآوری: هر روشی
2. آماده‌سازی: هر نوع داده‌ای (در حالیکه مجموعه داده در حال جمع‌آوری است) کار می‌کند.
3. تحلیل: هر روشی
4. آموزش: استفاده از روش اپریوری برای یافتن مجموعه اقلام مکرر
5. تست: اعمال نمی‌شود.
6. کاربرد: این راهکار برای پیدا کردن مجموعه اقلام مکرر و قواعد وابستگی بین اقلام به کار می‌رود.

فیلم آموزش داده کاوی Data Mining در متلب MATLAB در فرادرس

کلیک کنید

پیدا کردن مجموعه اقلام مکرر

راهکار جهت پیدا کردن مجموعه اقلام مکرر استفاده از الگوریتم اپریوری است. این الگوریتم نیازمند آن است که حداقل میزان اطمینان (Support) به عنوان ورودی به آن داده شود. الگوریتم، لیستی از همه اقلام کاندید با یک آیتم را فراهم می‌کند. سپس، مجموعه داده تراکنشی به منظور بررسی آنکه کدام مجموعه‌ها دارای حداقل سطح پشتیبان هستند اسکن می‌شود.

فیلم آموزش یادگیری ماشین و پیاده سازی در پایتون Python – بخش یکم در فرادرس

کلیک کنید

مجموعه‌هایی که حداقل سطح پشتیبان را ندارند، حذف می‌شوند. مجموعه داده‌های باقیمانده ترکیب می‌شوند تا مجموعه اقلام دارای دو آیتم حاصل شوند. دوباره، مجموعه داده تراکنشی اسکن می‌شود و مجموعه اقلامی که دارای حداقل سطح پشتیبانی نیستند، بیرون انداخته می‌شوند. این روال تا زمانی که همه مجموعه‌ها حذف شوند ادامه می‌یابد.

اسکن کردن مجموعه داده

برای هر تراکنش در مجموعه داده:

برای هر مجموعه اقلام مکرر:

1Check to see if can is a subset of tran
2If so increment the count of can

برای هر مجموعه اقلام مکرر کاندید:

اگر پشتیبان به آستانه حداقلی می‌رسد، آن آیتم را نگه دارد

لیست مجموعه اقلام مکرر را بازگردان

In [1]:

1from numpy import *

یک مجموعه داده ساده برای تست بساز

In [2]:

1def loadDataSet():
2    return [[1, 3, 4], [2, 3, 5], [1, 2, 3, 5], [2, 5]]

قطعه کد بالا، C1 را می‌سازد. C1، مجموعه اقلام مکرر کاندید با سایز یک است. در الگوریتم اپریوری C1 ساخته و سپس کل مجموعه داده به منظور بررسی آنکه آیا یک مجموعه اقلام حداقل آستانه لازم برای پشتیبانی را دارا است یا خیر، اسکن می‌شود. مجموعه داده‌ای که دارای حداقل آستانه است به L1 مبدل خواهد شد. L1 ترکیب می‌شود تا C2 ساخته شود و C2 فیلتر می‌شود تا به L2 تبدیل شود. Frozensets، مجموعه‌هایی هستند که فریز شده‌اند تا غیر قابل تغییر باشند. به جای set، نیاز به استفاده از frozenset‌ها است، زیرا در ادامه از این مجموعه‌ها به عنوان کلید در دیکشنری (dictionary) استفاده خواهد شد.

فیلم آموزش یادگیری ماشین و پیاده سازی در پایتون Python – بخش دوم در فرادرس

کلیک کنید

نمی‌توان یک مجموعه را تنها با یک عدد صحیح (integer) در پایتون ساخت. برای این کار نیاز به استفاده از لیست (list) است. به همین دلیل است که لیستی از لیست‌های تک آیتمی ساخته می‌شود. در نهایت، لیست باید مرتب‌سازی، هر آیتم در لیست به ()frozenset نگاشت و در نهایت لیست frozenset‌ها بازگردانده شود.

In [11]:

1def createC1(dataSet):
2    C1 = []
3    for transaction in dataSet:
4        for item in transaction:
5            if not [item] in C1:
6                C1.append([item])
7                
8    C1.sort()
9    return list(map(frozenset, C1))#use frozen set so we
10                            #can use it as a key in a dict

این تابع سه آرگومان مجموعه داده (Ck)، لیستی از مجموعه‌های کاندید و minSupport را دریافت می‌کند. minSupport حداقل پشتیبانی است که داده‌کاو انتظار دارد. کد زیر مربوط به تابعی است که برای تولید L1 از C1 استفاده می‌شود. علاوه بر این، تابع یک دیکشنری با مقادیر پشتیبان را باز می‌گرداند.

In [28]:

1def scanD(D, Ck, minSupport):
2    ssCnt = {}
3    for tid in D:
4        for can in Ck:
5            if can.issubset(tid):
6                if not can in ssCnt: ssCnt[can]=1
7                else: ssCnt[can] += 1
8    numItems = float(len(D))
9    retList = []
10    supportData = {}
11    for key in ssCnt:
12        support = ssCnt[key]/numItems
13        if support >= minSupport:
14            retList.insert(0,key)
15        supportData[key] = support
16    return retList, supportData

In [29]:

1dataSet = loadDataSet()
2dataSet

Out[29]:

In [30]:

1C1 = createC1(dataSet)

In [31]:

1C1

Out[31]:

C1 شامل لیستی از همه آیتم‌های موجود در frozenset است.

In [32]:

1#D is a dataset in the setform.
2
3D = list(map(set,dataSet))

In [33]:

1D

Out[33]:

اکنون همه چیز به شکل مجموعه موجود است و می‌توان آیتم‌هایی که حداقل پشتیبان را ندارند، حذف کرد.

In [34]:

1L1,suppDat0 = scanD(D,C1,0.5)
2L1

Out[34]:

چهار آیتم مشخص شده در بالا، لیست L1 را می‌سازند، این همان لیست مجموعه‌های تک آیتمی است که در حداقل ۵۰٪ از تراکنش‌ها به وقوع می‌پیوندند. آیتم ۴ حداقل سطح پشتیبانی را ندارد، بنابراین بخشی از L1 محسوب نمی‌شود. با حذف آن، چیزهای بیشتری نسبت به زمانی که مجموعه‌های دو آیتمی کشف می‌شوند حذف شده است.

فیلم آموزش کشف داده های پرت در یادگیری ماشین (رایگان) در فرادرس

کلیک کنید

شبه کد الگوریتم اپریوری

در حالیکه تعداد آیتم‌های موجود در مجموعه بزرگ‌تر از صفر است:

1Create a list of candidate itemsets of length k
2Scan the dataset to see if each itemset is frequent
3Keep frequent itemsets to create itemsets of length k+1

تابع اصلی ()apriori است. این تابع ()aprioriGen را برای ساخت مجموعه اقلام کاندید فراخوانی می‌کند (Ck). تابع ()aprioriGen لیستی از اقلام مکرر (Lk)، و ابعاد مجموعه اقلام (K) را دریافت می‌کند تا Ck را بسازد. برای مثال، مجموعه اقلام {0}، {1} و {2} را دریافت کرده و  {0,1}، {0,2} و {1,2} را می‌سازد. این مجموعه‌ها با استفاده از اتحاد مجموعه‌ها با یکدیگر ترکیب می‌شوند. نماد اتحاد در پایتون همانطور که پیش از این بیان شد، «|» است.

In [35]:

1def aprioriGen(Lk, k): #creates Ck
2    retList = []
3    lenLk = len(Lk)
4    for i in range(lenLk):
5        for j in range(i+1, lenLk): 
6            L1 = list(Lk[i])[:k-2]; L2 = list(Lk[j])[:k-2]
7            L1.sort(); L2.sort()
8            if L1==L2: #if first k-2 elements are equal
9                retList.append(Lk[i] | Lk[j]) #set union
10    return retList

In [38]:

1def apriori(dataSet, minSupport = 0.5):
2    C1 = createC1(dataSet)
3    D = list(map(set, dataSet))
4    L1, supportData = scanD(D, C1, minSupport)
5    L = [L1]
6    k = 2
7    while (len(L[k-2]) > 0):
8        Ck = aprioriGen(L[k-2], k)
9        Lk, supK = scanD(D, Ck, minSupport)#scan DB to get Lk
10        supportData.update(supK)
11        L.append(Lk)
12        k += 1
13    return L, supportData

In [39]:

1L,suppData = apriori(dataSet)

In [40]:

1L

Out[40]:

L شامل لیست‌هایی از مجموعه اقلام مکرر است که دارای حداقل پشتیبان ۰.۵ هستند. متغیر suppData، یک دیکشنری با مقادیر پشتیبان مجموعه اقلام این مطلب است.

In [46]:

1L[0]

Out[46]:

In [47]:

1L[1]

Out[47]:

In [48]:

1L[2]

Out[48]:

In [49]:

1L[3]

Out[49]:

In [50]:

1aprioriGen(L[0],2)

Out[50]:

کاوش قواعد وابستگی از مجموعه اقلام مکرر

برای کشف قواعد وابستگی، کار با یک مجموعه اقلام مکرر آغاز می‌شود. داده‌کاو می‌داند که این مجموعه اقلام یکتا هستند، اما قصد دارد بررسی کند که آیا می‌توان نکته دیگری از آن استخراج کرد. یک آیتم یا یک مجموعه از اقلام می‌تواند دلالت ضمنی بر دیگر آیتم داشته باشد. ()generateRules دستور اصلی است که دو دستور دیگر را فراخوانی می‌کند.

فیلم آموزش داده کاوی Data Mining در متلب MATLAB در فرادرس

کلیک کنید

تابع ()generateRules، سه ورودی دریافت می‌کند. این ورودی‌ها عبارتند از لیست مجموعه اقلام مکرر، یک دیکشنری از داده‌های پشتیبان برای آن اقلام و یک آستانه حداقل اطمینان. این تابع قرار است لیستی از قواعد با مقدار اطمینان آن‌ها را تولید کند تا بتوان بعدا آن‌ها را بر اساس این مقدار مرتب‌سازی کرد.

In [51]:

1def generateRules(L, supportData, minConf=0.7):  #supportData is a dict coming from scanD
2    bigRuleList = []
3    for i in range(1, len(L)):#only get the sets with two or more items
4        for freqSet in L[i]:
5            H1 = [frozenset([item]) for item in freqSet]
6            if (i > 1):
7                rulesFromConseq(freqSet, H1, supportData, bigRuleList, minConf)
8            else:
9                calcConf(freqSet, H1, supportData, bigRuleList, minConf)
10    return bigRuleList

()calcConf اطمینان قواعد را محاسبه و سپس بررسی می‌کند که کدام قواعد حداقل اطمینان (آستانه اطمینان) را دارند.

In [53]:

1def calcConf(freqSet, H, supportData, brl, minConf=0.7):
2    prunedH = [] #create new list to return
3    for conseq in H:
4        conf = supportData[freqSet]/supportData[freqSet-conseq] #calc confidence
5        if conf >= minConf: 
6            print (freqSet-conseq,'-->',conseq,'conf:',conf)
7            brl.append((freqSet-conseq, conseq, conf))
8            prunedH.append(conseq)
9    return prunedH

()rulesFromConseq قواعد وابستگی بیشتری از مجموعه داده اولیه تولید می‌کند. این تابع، مجموعه اقلام مکرر و H که لیستی از اقلامی که می‌توانند در سمت راست قاعده باشند را دریافت می‌کند.

In [54]:

1def rulesFromConseq(freqSet, H, supportData, brl, minConf=0.7):
2    m = len(H[0])
3    if (len(freqSet) > (m + 1)): #try further merging
4        Hmp1 = aprioriGen(H, m+1)#create Hm+1 new candidates
5        Hmp1 = calcConf(freqSet, Hmp1, supportData, brl, minConf)
6        if (len(Hmp1) > 1):    #need at least two sets to merge
7            rulesFromConseq(freqSet, Hmp1, supportData, brl, minConf)

In [55]:

1L,suppData= apriori(dataSet,minSupport=0.5)

In [56]:

1rules= generateRules(L,suppData, minConf=0.7)

حاصل اجرای کد بالا سه قاعده زیر است.

{1} ➞ {3}

{5} ➞ {2}

{2} ➞ {5}

نکته جالب توجه آن است که قواعد دارای ۲ و ۵ قابل معکوس شدن هستند، اما قاعده دارای ۱ و ۳ اینچنین نیست.

فیلم آموزش اصول و روش های متن کاوی Text Mining در فرادرس

کلیک کنید

کشف ویژگی‌های مشابه در قارچ‌های سمی

در ادامه چگونگی کشف ویژگی‌های مشابه در قارچ‌های سمی با استفاده از الگوریتم اپریوری و کد پایتون آمده است.

In [70]:

1mushDatSet = [line.split() for line in open('mushroom.dat').readlines()]

In [71]:

1L,suppData= apriori(mushDatSet, minSupport=0.3)

با استفاده از قطعه کد زیر، اقلام مکرر در ویژگی سمی ۲ جست‌و‌جو می‌شوند.

 In [73]:

1for item in L[1]:
2    if item.intersection('2'):
3        print (item)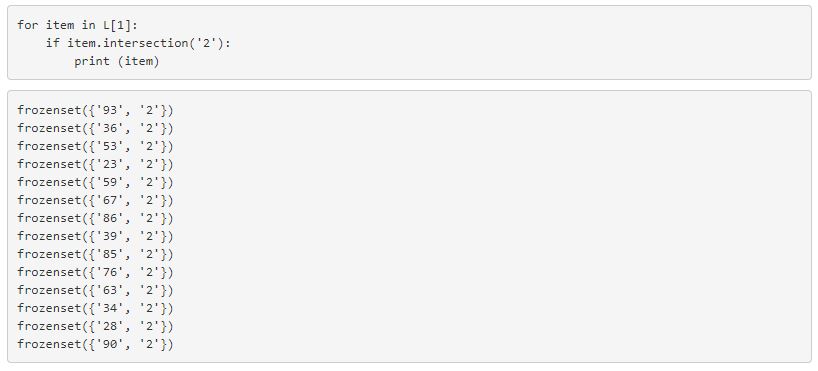

می‌توان این کار را برای مجموعه اقلام بزرگ‌تر تکرار کرد.

In [79]:

1for item in L[6]:
2    if item.intersection('2'):
3        print (item)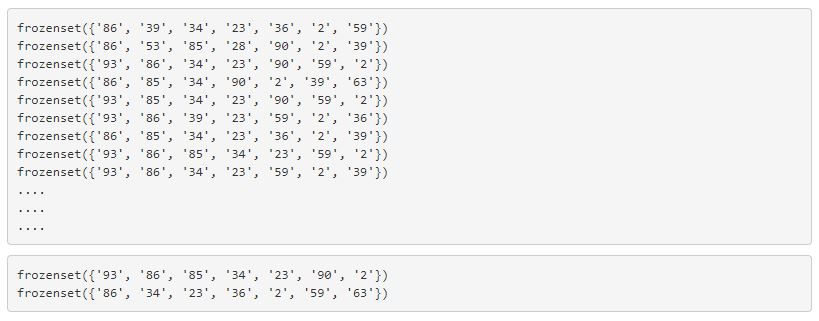

In [83]:

1rules= generateRules(L,suppData, minConf=0.7)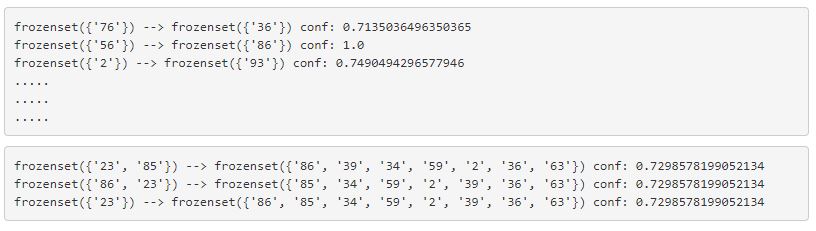

اگر نوشته بالا برای شما مفید بود، آموزش‌های زیر نیز به شما پیشنهاد می‌شوند:

• مجموعه آموزش‌های آمار، احتمالات و داده‌کاوی
• آموزش برنامه‌نویسی پایتون – مقدماتی
• آموزش برنامه‌نویسی یادگیری عمیق با پایتون (TensorFlow و Keras)
• مجموعه آموزش‌های برنامه نویسی متلب (MATLAB)
• مجموعه آموزش‌های هوش محاسباتی

^^