سیستم های عددی – ریاضیات به زبان ساده

طرز فکر همه افراد در طی زمان تغییر می‌یابد. همه افراد دوست دارند روش‌های جدیدی برای حل مشکلات خود پیدا کنند. ما نیز در این نوشته تلاش می‌کنیم تا نگاهی نو به سیستم های عددی داشته باشیم. در این نوشته با ما همراه باشید تا شما نیز از این نگاه متفاوت بهره‌مند شوید. اما شاید بپرسید دلیل اهمیت این داشتن نگاه متفاوت چیست؟

• ممکن است فکر کنید ریاضیات یکی از چندین رویکرد ممکن است. در هر حال ما در این نوشته دانش خود از سیستم‌های عددی را بهبود می‌بخشیم.
• شما با مطالعه این نوشته متوجه روابط اصلی بین اعداد خواهید شد و از آن‌ها در حوزه‌های متنوعی استفاده خواهید کرد.
• در مورد مفاهیم عجیبی مانند تقسیم بر صفر و اعداد موهومی دیدگاه‌های جدیدی کسب می‌کنید.

ریاضیات، نرم‌افزار ذهن شما است

علی‌رغم این که دایره المعارف ها دوست دارند ریاضیات را به صورت «دانشی که بر روی مفاهیمی از قبیل کمیت، ساختار، فضا و تغییر متمرکز شده است» توصیف کنند؛ اما واقعیت این است که ریاضیات چیزی فراتر از این است. در واقع ریاضیات شبیه یک نرم‌افزار برای مغز ما عمل می‌کند.

• مغز شما یک رایانه خالی است.
• شما با یادگیری ریاضیات (نصب نرم‌افزار شمارش 1.0 و جبر XY پرو) به ناگاه توانایی حل انواع جدیدی از مسائل را می‌یابید.
• ریاضیات در مواردی باگ دارد. برای مثال اعداد رومی نسخه 1.0 مشکلی ندارند؛ اما اعداد اعشاری نسخه 2.0 نیاز به ارتقا دارند. اما برخی مسائل هم هستند که همچنان مشکلاتی دارند مانند تقسیم بر صفر.

گرچه این قیاس تا حدودی غریب است؛ اما اگر کمی در آن تأمل کنید، متوجه می‌شوید که عاری از حقیقت نیست.

ریاضیات نیز محدودیت‌های خاص خود را دارد

معمای سریع: آیا می‌توانید دو عدد رومی را در هم ضرب کنید؟ البته نباید تقلب کرده و آن‌ها را به اعداد ده‌دهی ضرب کنید. ما در مورد ضرب «IX در XXXIV» صحبت می‌کنیم.

اگر چنین مهارتی داشته باشید، متوجه خواهید شد که پاسخ CCCVI است. آیا این تجربه وحشتناک به این معنی است که ریاضیات سخت است؟ یا شاید ما به روش نادرستی در مورد ضرب عمل می‌کنیم و در واقع نرم‌افزار ذهنی نادرستی را نصب کرده‌ایم؟

اگر ذهن خود را از «اعداد رومی I» به «اعداد ده‌دهی 2.0» ارتقا دهید، متوجه می‌شوید که محاسبه حاصلضرب 9 در 34 سؤال بسیار ساده‌تری است. پس از کمی محاسبه، پاسخ 306 خواهد بود. می‌بینید که همین مسئله وقتی با استفاده از نرم‌افزار ذهنی متفاوتی بررسی می‌شود، بسیار ساده‌تر خواهد شد.

نقاشی با Notepad

البته که شما می‌توانید با سیستم اعداد رومی نیز ضرب را انجام دهید؛ ولی این کار نه آسان است و نه جالب. همچنین کمکی به انجام محاسبات پیچیده نمی‌کند. در واقع دشواری‌ها غالباً ناشی از رویکردهای ما هستند و نه خود مفاهیم.

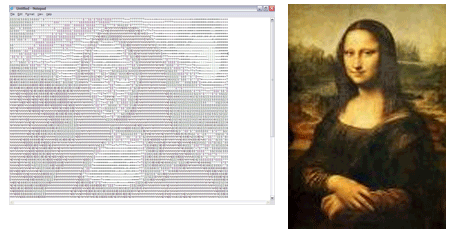
وضعیتی که در بخش فوق توصیف کردیم، شبیه این است که بخواهیم با نرم‌افزار Notepad ویندوز نقاشی کنیم. نُت پد ابزار خوبی است و حتی می‌توانید در آن نقاشی مونالیزا را تایپ کنید؛ اما کسی که این نرم‌افزار را طراحی کرده، هرگز به تصاویر فکر نمی‌کرده است.

اعداد رومی نیز زمانی ایجاد شده‌اند که بشر هنوز در حال یادگیری شمارش بوده است، در چنان زمانی هنوز عدد صفر اختراع نشده بود! ریاضیات یک سیستم نرم‌افزاری است که در طی زمان بهبود یافته و اعداد رومی نیز در این گذار ارتقا یافته‌اند.

اما پیش از آن که از این همه پیشرفت و ارتقا و به‌روزرسانی خوشحال شویم، باید یادآوری کنیم که سیستم عددی که در حال حاضر استفاده می‌کنیم هم یک وصله از ویژگی‌های جدید و اصلاح باگ‌ها است که برای بهبود درک ما از جهان ابداع شده است.

در مواردی نیز در همین سیستم عددی حاضر، با دشواری‌هایی مواجه می‌شویم. برای مثال نتیجه تقسیم بر صفر چیست؟ و یا جذر 1- کدام است؟ در این موارد ممکن است کنجکاو شویم که آیا این محدودیت‌ها که برخورد کرده‌ایم، قواعدی جهانی هستند یا صرفاً دیواره‌هایی هستند که خودمان ساخته‌ایم؟

ما می‌توانیم همانند روش ضرب رومی‌ها صرفاً از کسرها استفاده کنیم و این روش خوبی محسوب می‌شود.

از زمان باستان تا بی‌نهایت

سیستم عددی ما در طی زمان تکامل یافته است. بشر در ابتدا با استفاده از انگشت‌های خود شروع به شمارش کرد و سپس برای شمارش از اشیای غیر جاندار مانند ترسیم خط روی شن استفاده نمود. سپس با ابداع صفر به سمت اعداد رومی (میانبرهایی برای اعداد بزرگ‌تر) و اعداد عربی (سیستم ده‌دهی) حرکت کرد.

فیلم آموزش مقدماتی نرم افزار میپل – انجام محاسبات ریاضی با Maple در فرادرس

کلیک کنید

در این مسیر ما دریافتیم که در سیستم عددی ما باگ‌هایی وجود دارد و بنابراین روش‌های جدیدی برای حل آن‌ها ابداع کردیم. در این مورد نیز در واقع باگ در طرز فکر ما (نرم‌افزار ذهنی) بوده است.

نرم‌افزار قدیمی

نرم‌افزار قدیمی شمارش، یک سیستم عددی بود که از سوی انسان غار نشین ابداع شد. در این سیستم برای شمارش از انگشتان دست و پا استفاده می‌شد. باگ این سیستم آن بود که محدود به شمارش 20 شیء بود.

اصلاحیه‌ای که برای این سیستم آمد این بود که افراد متوجه شدند برای شمارش به اشیای فیزیکی نیاز ندارند، یعنی برای شمارش 20 گاو لازم نیست که 20 گاو داشته باشید. می‌توانید 20 خط روی زمین بکشید یا از میانبری مانند C برای نمایش عدد 100 استفاده کنید.

سیستم خطوط و اعداد رومی

زمانی که این روش انتزاعی نمایش اعداد کشف شد، امکان انجام کارهای جالب و ایجاد میانبرهای مختلف حتی برای اعداد بسیار بزرگ پدید آمد: برای مثال: I + II = III، X + XX = XXX.

اما همچنان چند باگ وجود داشت: حاصل III – III چیست؟

صفر

کشف عدد صفر یک کشف بسیار جذاب و زیبا بوده است. استفاده از نماد 0 برای نمایش هیچ! این یک ایده بسیار هوشمندانه و کاربردی است. ما می‌توانیم همچنان وضعیت عدم وجود هیچ گاوی را نیز معین کنیم! در مورد خواستگاه عدد صفر نقل قول های زیادی وجود دارد؛ اما طبق آخرین تحقیق‌های باستان‌شناسی نخستین سند استفاده از صفر به معنی امروزی در یک مجموعه از اوراق برگ خشخاش مشاهده شده که در روستای باکشالی پاکستان پیدا شده است. تصویر ابتدای این نوشته نیز همین سند را نشان می دهد که اینک در دانشگاه آکسفورد قرار دارد.

کشف عدد صفر  پیشرفت منجر به ایجاد سیستم عددی شد که برای ما کاملاً آشنا است. 204 یعنی دو تا 100، صفر تا 10 و چهار تا 1. بدین ترتیب تقسیم و ضرب عدد صحیح به روشی امکان‌پذیر شد که رومی‌ها و دوستان غارنشین ما حتی نمی‌توانستند به آن فکر کنند. اگر به شما زمان کافی بدهند، می‌توانید حاصلضرب 5678 × 1234 را محاسبه کنید. این یک ویژگی عالی سیستم عددی جدید است.

اعداد منفی

اما معرفی صفر همه مشکلات را حل نمی‌کرد. تفریق همچنان یک مشکل محسوب می‌شد. از 3 مقدار 5 را کسر کنیم چه اتفاقی می‌افتد؟ راه‌حل ما این است که 3 انگشت خود را جمع کنیم و بعد چه؟ می‌بینیم که این یک باگ و در واقع وضعیت تعریف نشده‌ای است؛ اما این مشکل نیز در ادامه حل شد.

ما می‌توانیم در مورد مسائل مختلف به روش متفاوتی فکر کنیم و این امکان را خلق نماییم که عددی منفی باشد. عددی که کمتر از هیچ است! اگر به دقت تأمل کنید، متوجه می‌شوید که کشف واقعاً مهمی است.

تفسیرهای مختلفی برای اعداد منفی وجود دارد. برای مثال کسری گاو یا بدهی گاو. این تفسیرها برای مدیریت این باگ در تفریق بوده است. البته چند هزار سال طول کشید تا این ویژگی جدید پذیرفته شود. اعداد منفی تنها در سال‌های 1700 بود که مرسوم شدند.

اعداد رومی

تقسیم نیز باعث ورود برخی باگ‌ها در سیستم عددی رومی شد. $${8 \over 4}$$ مشکلی ایجاد نمی‌کرد؛ اما $${3 \over 4}$$ یک باگ محسوب می‌شد. اصلاحیه ‌این باگ این بود که روشی بیابیم تا «اعداد بین دو عدد» را نمایش دهیم. $${3 \over 4}$$ در حقیقت $${75 \over 100}$$ یا 0.75 است.

ما برای مدیریت ایده‌ی دیوانه‌وار عددی بزرگ‌تر از 0 ولی کوچک‌تر از 1، مفهومی به نام نقطه اعشار را ابداع کردیم. واقعاً که کشف اعجاب‌انگیزی بوده است. بشر این نوع اعداد عجیب را برای بهبود نرم‌افزار ذهنی خود ابداع کرد. کسرها در هر صورت کاربردهای خاص خود را دارند. برای مثال ممکن است در اخبار بشنوید که هر خانواده به طور میانگین 2.3 فرزند دارد و با این وجود از شنیدن این خبر شگفت‌زده نشوید.

اعداد گنگ باعث ناراحتی یونانی‌ها می‌شد

فرض کنید نشسته‌ایم و مشغول محاسبات خود هستیم که ناگاه با مثلثی قائم‌الزاویه مواجه می‌شویم که اندازه دو ضلع غیر وتر آن برابر با 1 است. متوجه می‌شویم که طول وتر آن برابر با ریشه دوم 2 است. اگر از ما خواسته شود این عدد را بنویسیم باعث ترس ما می‌شود. ما نمی‌توانیم این عدد را بنویسیم چون عددی اعشاری با بخش اعشاری نامتناهی و غیر تکراری است که نمی‌توان به صورت یک کسر آن را نوشت. با این حال گرچه نمی‌توانیم آن را بنویسیم؛ اما همچنان آنجا روی کاغذ است.

برای توصیف این وضعیت عبارت «بغرنج» کافی نیست. این خود جنون است. مشهور است که فردی که این اعداد را کشف کرد به دریا انداختند.

خوشبختانه اعداد گنگ، جبری هستند یعنی می‌توان آن‌ها را به عنوان پاسخ برخی معادله‌های جبری ارائه کرد. برای مثال 2√ را می‌توان به عنوان پاسخ معادله x² = 2 در نظر گرفت. اما ما اغلب فراموش می‌کنیم که 9√ هم برابر با 3 و هم 3- است. به طور معمول ما فقط ریشه مثبت را در نظر می‌گیریم.

اعداد مختلط (complex)

در این مرحله یک فرد باهوش ممکن است بپرسد «خب چه عددی را می‌توان به عنوان پاسخ معادله x² = -1 در نظر گرفت؟»

چه باید کرد؟ یک راه‌حل این است که اعلام کنیم این معادله مانند عدد صفر، اعداد کسری، اعداد گویا و اعداد گنگ که زمانی «ناممکن و بی‌معنی» بودند، به حالت تعریف نشده و بی‌معنی است. یک راه‌حل دیگر هم این است که بپذیریم که درک بشر از جهان کامل نیست و ما باید چیزهای بیشتر را بیاموزیم. البته شما می‌دانید که کدام پاسخ صحیح‌تر است.

اعداد موهومی (Imaginary) به عنوان زیر مجموعه‌ای از اعداد مختلط، دقیقاً به اندازه همه اعداد دیگر واقعی هستند. همچنین می‌توان گفت که اعداد موهومی همان قدر غیر واقعی هستند که همه اعداد دیگر هستند. اما ما درک شهودی از آن‌ها نداریم، چون در اغلب موارد برای ما چنین توضیح داده شده است که اگر مدرک مهندسی برق نداشته باشید و اگر در مورد امپدانس پیچیده معلوماتی نخوانده باشید، نمی‌توانید درکی شهودی از اعداد موهومی داشته باشید.

در این نوشته قصد داریم شما را با درک شهودی اعداد موهومی بیشتر آشنا کنیم؛ اما برای این مسئله هنوز باید کمی صبر کنید.

چرا 1 =...0.999 است و چرا باید این مسئله برای شما مهم باشد؟

سیستم عددی ما در واقع روش تفکر ما است؛ اما همچنان چند شکاف در آن وجود دارد. ما در مورد روش برخورد با اعداد بی‌نهایت کوچک و بی‌نهایت کاملاً مطمئن نیستیم.

برای مثال به گفتگوی زیر توجه کنید:

• $${1 \over 3}$$ چیست؟
• خب یعنی $$\overline{0.33}$$ و تکرار این 3 ها (دوره گردش).
• خیلی خوب. حالا $${{1 \over 3} + {1 \over 3}}$$ یعنی چه؟
• یعنی $${2 \over 3}$$.
• کاملاً درست است؛ اما اگر بخواهیم آن را به صورت اعشاری بنویسیم چطور؟
• خب $$\overline{0.33}$$ به اضافه $$\overline{0.33}$$، برابر با $$\overline{0.66}$$ خواهد بود.
• عالی است. حال بگویید $${{1 \over 3} + {1 \over 3} + {1 \over 3}}$$ در سیستم اعشاری یعنی چه؟
• خب $$\overline{0.33}$$ به علاوه $$\overline{0.33}$$  به علاوه $$\overline{0.33}$$ ، برابر خواهد بود با $$\overline{0.99}$$.
• اما بنا بر گفته شما $${{1 \over 3} + {1 \over 3} + {1 \over 3}}$$ برابر با 1 نمی‌شود. از طرفی می‌دانیم که $$\overline{0.9}$$ دوره گردش برابر با 1 است!

اگر این استدلال را برای یک کودک یا حتی بزرگسال توضیح دهید، واکنش‌های جالبی از وی خواهید دید! بدیهی است که $${1 \over 3}$$ + $${1 \over 3}$$+ $${1 \over 3}$$ = 1؛ اما چرا وقتی آن‌ها را به صورت اعشار با هم جمع می‌کنیم، حاصل کمی عجیب به نظر می‌رسد؟ در این مورد نیز سؤال اینجا است که این عجیب بودن در مفهوم است یا طرز فکر ما؟

خب ابتدا باید بدانیم منظور ما از $$\overline{0.33}$$ چیست؟ آیا یک میمون وجود دارد که این 3 ها را تا ابد پشت سر هم می‌نویسد؟ آیا این عددی است که فراتر از روش نمادگذاری ما است و ما امیدوار هستیم بتوانیم آن را همانند جذر 2 تخمین بزنیم؟ اگر از مبنای 3 استفاده کنیم این مشکل رفع می‌شود. $${1 \over 3}$$ = 0.1 در مبنای 3 است. بنابراین 0.1 + 0.1 + 0.1 = 1 در مبنای 3 است.

اما چرا این مسئله مهم است؟

آیا زمان ارتقای دیگری در سیستم اعداد فرا رسیده است؟ بررسی بی‌نهایت در سیستم عددی کنونی ما شبیه ترسیم نقاشی با نت پد است. این مفهوم زمخت و تا حدودی فریب‌آمیز به نظر می‌رسد. مثلاً می‌گوییم $${1 \over 0}$$ برابر با بی‌نهایت است. خب در مورد $${2 \over 0}$$ یا $${3 \over 0}$$ چه می‌توان گفت؟

ریاضیدان‌ها مشغول کار بر روی سیستم‌های عددی جدیدی هستند که در آن بی‌نهایت نیز گنجانده شده است؛ اما همچنان مشکلاتی در مورد روش شمارش بی‌نهایت وجود دارد. اگر به لحظه‌ای که فردی مفهوم صفر، اعداد کسری و اعداد منفی را به صورتی قابل درک و نه صرفاً پاسخ یک معادله در آورد بیندیشیم، متوجه خواهیم شد که می‌توانیم بر همه مشکلات ریاضیاتی فائق آییم.

جمع‌بندی

در این نوشته تلاش کردیم تا

• نشان دهیم که ریاضیات چقدر شبیه نرم‌افزار ذهنی است که در طی زمان بهبود یافته است.
• مفاهیم بی‌معنی مانند صفر یا اعداد منفی می‌توانند در آغاز شبیه پارادوکس باشند؛ ولی با اتخاذ رویکرد صحیح، شهود قابل قبولی در مورد آن‌ها به دست می‌آید.
• امروزه همچنان در مورد ایده‌هایی مانند بی‌نهایت، با مشکل مواجه هستیم و باید این واقعیت را بپذیریم.

روش تفکر در مورد ریاضیات باید چنین باشد یعنی آن را با درک خود ترکیب کنیم. نباید به خاطر این که نمی‌دانیم معنی دقیق $${1 \over 3}$$ چیست منفعل شویم و از جمع کردن دست بکشیم.

بینش‌هایی که به دست می‌آوریم باعث تعمیق درک ما می‌شود؛ اما گاهی اوقات تنها در عمل است که این بینش‌ها به دست می‌آیند. نیوتن زمانی که حسابان را توسعه می‌داد درکی رسمی از مقادیر بسیار کوچک نداشت؛ اما متوجه شد که برای منظور وی مفید هستند و باعث حل معادلات می‌شوند. البته ما طرفدار ایده عمل بدون فکر نیستیم؛ اما در برخی موارد باید قبل از این که بینش‌هایی به دست آید کمی چکش‌کاری نمود.

اگر این نوشته مورد توجه شما واقع شده است، احتمالاً به موارد زیر نیز علاقه‌مند خواهید بود:

• عدد اویلر یا نپر – به زبان ساده
• آموزش آزمون های استخدامی – ریاضی و آمار
• اعداد حقیقی – به زبان ساده
• آموزش ریاضی پایه دانشگاهی
• اعداد مختلط – به زبان ساده
• مجموعه آموزش‌های ریاضیات

==