در آموزشهای پیشین مجله فرادرس، با مفهوم معادلات دیفرانسیل آشنا شدیم و انواع معادلات دیفرانسیل و روشهای حل آنها را بیان کردیم. در این آموزش، تعدادی نمونه سوال معادلات دیفرانسیل را همراه با جواب آنها بررسی میکنیم.
روش حل نمونه سوال معادلات دیفرانسیل
همانطور که در آموزشهای گذشته مجله فرادرس دیدیم، نمونه سوال معادلات دیفرانسیل را میتوان در دستههای مختلفی قرار داد و برای هریک، با توجه به ساختارشان، یک روش حل مناسب ارائه کرد. پیش از حل نمونه سوال معادلات دیفرانسیل بهتر است با انواع آنها و روش حلشان آشنا شویم.
در مجله فرادرس، همه انواع معادلات دیفرانسیل کتابهای درسی پوشش داده شدهاند و با جستو جو در مجله فرادرس، میتوانید موضوع مورد نظرتان را یاد بگیرید. برخی از موضوعات مرتبط با معادلات دیفرانسیل مجله فرادرس که برای حل نمونه سوال معادلات دیفرانسیل میتوانید از آنها کمک بگیرید، به شرح زیر هستند:
علاوه بر آموزشهایی که بیان کردیم، میتوانید از تقلبنامه معادلات دیفرانسیل نیز میتوانید برای حل نمونه سوال معادلات دیفرانسیل استفاده کنید. این تقلبنامه، بهویژه برای مرور فرمولها پیش از امتحان مفید خواهد بود. تقلبنامه معادلات دیفراسیل را میتوانید از این لینک دانلود کنید.
نمونه سوال معادلات دیفرانسیل با جواب
در این بخش، به حل چند نمونه سوال معادلات دیفرانسل میپردازیم.
نمونه سوال معادلات دیفرانسیل ۱
معادله دیفرانسیل d y d x = y ( y + 2 ) { \frac { { d y } } { { d x } } \normalsize } = y \left ( { y + 2 } \right ) d x d y = y ( y + 2 )
حل سوال ۱: در معادله بالا، p ( x ) = 1 p\left( x \right) = 1 p ( x ) = 1 h ( y ) = h ( y ) = y ( y + 2 ) h \left ( y \right ) = h \left ( y \right ) = y \left ( { y + 2 } \right ) h ( y ) = h ( y ) = y ( y + 2 ) h ( y ) h\left( y \right) h ( y ) d x dx d x
d y y ( y + 2 ) = d x . \frac { { d y } } { { y \left ( { y + 2 } \right ) } } = d x . y ( y + 2 ) d y = d x .
لازم به ذکر است که بعد از تقسیم، میتوان گفت وقتی h ( y ) h(y) h ( y ) y = 0 y=0 y = 0 y = − 2 y=-2 y = − 2 y = 0 y=0 y = 0
y = 0 , d y = 0. y = 0,\;\;dy = 0. y = 0 , d y = 0.
با جایگذاری روابط بالا در معادله، خواهیم داشت: 0 = 0 0 = 0 0 = 0 y = 0 y=0 y = 0 y = − 2 y= -2 y = − 2
به معادله دیفرانسیل برمیگردیم و از آن انتگرال میگیریم:
∫ d y y ( y + 2 ) = ∫ d x + C . { \int { \frac { { d y } } { { y \left ( { y + 2 } \right ) } } } } = { \int { d x } + C . } ∫ y ( y + 2 ) d y = ∫ d x + C .
انتگرال سمت چپ را میتوان با استفاده از تجزیه کسر انتگرالده محاسبه کرد:
$$ { \frac { 1 } { { y \left ( { y + 2 } \right ) } } = \frac { A } { y } + \frac { B } { { y + 2 } } , \; \; } \Rightarrow<br />
{ \frac { 1 } { { y \left ( { y + 2 } \right ) } } = \frac { { A \left ( { y + 2 } \right ) + B y } } { { y \left ( { y + 2 } \right ) } } , \; \; }\\ \Rightarrow<br />
{ 1 \equiv A y + 2 A + B y , \; \; } \Rightarrow<br />
{ 1 \equiv \left ( { A + B } \right ) y + 2 A , \; \; } \Rightarrow<br />
{ \left \{ { \begin {array} { * { 2 0 } { c } }<br />
{ A + B = 0 }\\<br />
{ 2 A = 1 }<br />
\end {array} } \right . , \; \; } \Rightarrow<br />
{ \left\{ { \begin {array} { * { 2 0 } { c } }<br />
{ A = \frac { 1 } { 2 } } \\<br />
{ B = – \frac { 1 } { 2 } }<br />
\end {array} } \right . . } $$
تجزیه انتگرالده به کسرهای جزئی بهصورت زیر است:
1 y ( y + 2 ) = 1 2 ( 1 y – 1 y + 2 ) . { \frac { 1 } { { y \left ( { y + 2 } \right ) } } } = { \frac { 1 } { 2 } \left ( { \frac { 1 } { y } – \frac { 1 } { { y + 2 } } } \right ) . } y ( y + 2 ) 1 = 2 1 ( y 1 – y + 2 1 ) .
بنابراین، میتوان نوشت:
1 2 ∫ ( 1 y – 1 y + 2 ) d y = ∫ d x + C , ⇒ 1 2 ( ∫ d y y – ∫ d y y + 2 ) = ∫ d x + C , ⇒ 1 2 ( ln ∣ y ∣ – ln ∣ y + 2 ∣ ) = x + C , ⇒ 1 2 ln ∣ y y + 2 ∣ = x + C , ⇒ ln ∣ y y + 2 ∣ = 2 x + 2 C . { { \frac { 1 } { 2 }\int { \left ( { \frac { 1 } { y } – \frac { 1 } { { y + 2 } } } \right ) d y } } = { \int { d x } + C , \;\; } } \Rightarrow { { \frac { 1 } { 2 } \left ( { \int { \frac { { d y } } { y } } – \int { \frac { { d y } } { { y + 2 } } } } \right ) } = { \int { d x } + C , \;\; } } \\ \Rightarrow { { \frac { 1 } { 2 } \left ( { \ln \left | y \right | – \ln \left | { y + 2 } \right | } \right ) } = { x + C , \;\; } } \Rightarrow { \frac { 1 } { 2 } \ln \left | { \frac { y } { { y + 2 } } } \right| = x + C,\;\;}\Rightarrow {\ln \left| {\frac{y}{{y + 2}}} \right| = 2x + 2C.} 2 1 ∫ ( y 1 – y + 2 1 ) d y = ∫ d x + C , ⇒ 2 1 ( ∫ y d y – ∫ y + 2 d y ) = ∫ d x + C , ⇒ 2 1 ( ln ∣ y ∣ – ln ∣ y + 2 ∣ ) = x + C , ⇒ 2 1 ln y + 2 y = x + C , ⇒ ln y + 2 y = 2 x + 2 C .
ثابت را بهصورت 2 C = C 1 2C = {C_1} 2 C = C 1
ln ∣ y y + 2 ∣ = 2 x + C 1 , y = 0 , y = – 2. {\ln \left| {\frac{y}{{y + 2}}} \right| = 2x + {C_1},\;\;\;}\kern-0.3pt{y = 0,\;\;\;}\kern-0.3pt{y = – 2.} ln y + 2 y = 2 x + C 1 , y = 0 , y = –2.
جواب معادله بهصورت ضمنی است. در این حالت میتوان عبارت بالا را بهصورت تابع صریح y = f ( x , C 1 ) y = f\left( {x,{C_1}} \right) y = f ( x , C 1 ) C 1 C_1 C 1
نمونه سوال معادلات دیفرانسیل ۲
معادله دیفرانسیل زیر را حل کنید و بازه اعتبار جواب معادله را بیابید.
y ′ = x y 3 1 + x 2 y ( 0 ) = − 1 y' = \frac { { x { y ^ 3 } } } { { \sqrt { 1 + { x ^ 2 } } } } \hspace{0.25in} y \left ( 0 \right ) = - 1 y ′ = 1 + x 2 x y 3 y ( 0 ) = − 1
حل سوال ۲: ابتدا معادله را جدا میکنیم، سپس از دو طرف انتگرال میگیریم:
y − 3 d y = x ( 1 + x 2 ) − 1 2 d x ∫ y − 3 d y = ∫ x ( 1 + x 2 ) − 1 2 d x − 1 2 y 2 = 1 + x 2 + c \begin {align*} { y ^ { - 3 } } d y & = x { \left ( { 1 + { x ^ 2 } } \right ) ^ { - \frac { 1} { 2 } } } \, d x \\ \int { { { y^ { - 3 } } d y } } & = \int { { x { { \left ( { 1 + { x ^ 2 } } \right ) } ^ { - \frac { 1 } { 2 } } } \, d x } } \\ - \frac { 1 } { { 2 { y ^ 2 } } } & = \sqrt { 1 + { x ^ 2 } } + c \end {align*} y − 3 d y ∫ y − 3 d y − 2 y 2 1 = x ( 1 + x 2 ) − 2 1 d x = ∫ x ( 1 + x 2 ) − 2 1 d x = 1 + x 2 + c
شرایط اولیه را در معادله اخیر قرار داده و مقدار ثابت c c c
− 1 2 = 1 + c c = − 3 2 - \frac { 1 } { 2 } = \sqrt 1 + c \hspace{0.25in} c = - \frac { 3 } { 2 } − 2 1 = 1 + c c = − 2 3
جواب ضمنی بهصورت زیر است:
− 1 2 y 2 = 1 + x 2 − 3 2 - \frac { 1 } { { 2 { y ^ 2 } } } = \sqrt { 1 + { x ^ 2 } } - \frac { 3 } { 2 } − 2 y 2 1 = 1 + x 2 − 2 3
اکنون، y ( x ) y ( x ) y ( x )
1 y 2 = 3 − 2 1 + x 2 y 2 = 1 3 − 2 1 + x 2 y ( x ) = ± 1 3 − 2 1 + x 2 \begin {align*} \frac { 1 } { { { y ^ 2 } } } & = 3 - 2 \sqrt { 1 + { x ^ 2 } } \\ { y ^ 2 } & = \frac { 1 } { { 3 - 2 \sqrt { 1 + { x ^ 2 } } } } \\ y \left ( x \right ) & = \pm \frac { 1 } { { \sqrt { 3 - 2 \sqrt { 1 + { x ^2 } } } } } \end {align*} y 2 1 y 2 y ( x ) = 3 − 2 1 + x 2 = 3 − 2 1 + x 2 1 = ± 3 − 2 1 + x 2 1
با اعمال دوباره شرایط اولیه، میبینیم که جواب منفی صحیح است. بنابراین، جواب صریح بهشکل زیر خواهد بود:
y ( x ) = − 1 3 − 2 1 + x 2 y \left ( x \right ) = - \frac { 1 } { { \sqrt { 3 - 2 \sqrt { 1 + { x ^ 2 } } } } } y ( x ) = − 3 − 2 1 + x 2 1
اکنون باید دامنه اعتبار جواب را بررسی کنیم. این کار آسانتر از آن چیزی است که فکر میکنید. از آنجا که 1 + x 2 ≥ 0 1 + {x^2} \ge 0 1 + x 2 ≥ 0 x x x
3 − 2 1 + x 2 > 0 3 > 2 1 + x 2 9 > 4 ( 1 + x 2 ) 9 4 > 1 + x 2 5 4 > x 2 \begin {align*} 3 - 2 \sqrt { 1 + { x ^ 2 } } & > 0\\ 3 & > 2 \sqrt { 1 + { x ^ 2 } } \\ 9 & > 4 \left ( { 1 + { x ^2 } } \right ) \\ \frac { 9 } { 4 } & > 1 + { x ^ 2 } \\ \frac { 5 } { 4 } & > { x ^ 2 } \end {align*} 3 − 2 1 + x 2 3 9 4 9 4 5 > 0 > 2 1 + x 2 > 4 ( 1 + x 2 ) > 1 + x 2 > x 2
توجه داشته باشید که توانستیم هر دو طرف نامساوی را به توان ۲ برسانیم، زیرا هر دو طرف آن در این حالت مثبت هستند. در نهایت با حل x x x x x x
− 5 2 < x < 5 2 - \frac{{\sqrt 5 }}{2} < x < \frac{{\sqrt 5 }}{2} − 2 5 < x < 2 5
که شامل شرایط اولیه x = 0 x = 0 x = 0
نمونه سوال معادلات دیفرانسیل ۳
معادله دیفرانسیل زیر را حل کند.
d y d t = e y − t sec ( y ) ( 1 + t 2 ) , y ( 0 ) = 0 \frac { {d y } } { { d t } } = { { \bf { e } } ^ { y \, - \,t } }\sec \left ( y \right ) \left ( { 1 + { t ^ 2 } } \right ), \hspace {0.25in} y \left ( 0 \right ) = 0 d t d y = e y − t sec ( y ) ( 1 + t 2 ) , y ( 0 ) = 0
حل سوال ۳: این مثال به کمی کار نیاز دارد تا آن را جدا کنیم و به شکلی بنویسیم که بتوانیم از آن انتگرال بگیریم:
d y d t = e y e − t cos ( y ) ( 1 + t 2 ) e − y cos ( y ) d y = e − t ( 1 + t 2 ) d t \begin {align*} \frac { { d y } } { { d t } } & = \frac { { { { \bf { e } } ^ y } { { \bf { e } } ^ { - t } } } } { { \cos \left ( y \right ) } } \left ( { 1 + { t ^2 } } \right ) \\ { { \bf { e } } ^ { - y } } \cos \left ( y \right ) \, d y & = { { \bf { e } } ^ { - t } } \left ( { 1 + { t ^ 2 } } \right ) d t \end {align*} d t d y e − y cos ( y ) d y = cos ( y ) e y e − t ( 1 + t 2 ) = e − t ( 1 + t 2 ) d t
اکنون، با انتگرالگیری از دو طرف تساوی، میتوانیم یک جواب ضمنی معادله را بهدست آوریم:
∫ e − y cos ( y ) d y = ∫ e − t ( 1 + t 2 ) d t e − y 2 ( sin ( y ) − cos ( y ) ) = − e − t ( t 2 + 2 t + 3 ) + c \begin {align*} \int { {{ { \bf { e } } ^ { - y } } \cos \left ( y \right ) \, d y } } & = \int { { { { \bf { e } } ^ { - t } } \left ( { 1 + { t ^ 2 } } \right ) dt } } \\ \frac { { { { \bf { e } } ^ { - \, y } } } } { 2 } \left ( { \sin \left ( y \right ) - \cos \left ( y \right ) } \right ) & = - { { \bf { e } } ^ { - t } } \left ( { { t ^ 2 } + 2 t + 3 } \right ) + c \end {align*} ∫ e − y cos ( y ) d y 2 e − y ( sin ( y ) − cos ( y ) ) = ∫ e − t ( 1 + t 2 ) d t = − e − t ( t 2 + 2 t + 3 ) + c
با اعمال شرایط اولیه، خواهیم داشت:
1 2 ( − 1 ) = − ( 3 ) + c c = 5 2 \frac { 1 } { 2 } \left ( { - 1 } \right ) = - \left ( 3 \right ) + c \hspace {0.25in} c = \frac { 5 } { 2 } 2 1 ( − 1 ) = − ( 3 ) + c c = 2 5
در نتیجه، جواب بهشکل زیر درمیآید:
e − y 2 ( sin ( y ) − cos ( y ) ) = − e − t ( t 2 + 2 t + 3 ) + 5 2 \frac { { { { \bf { e } } ^ { - y } } } } { 2 } \left ( { \sin \left ( y \right ) - \cos \left ( y \right ) } \right ) = - { { \bf { e } } ^ { - t } } \left ( { { t ^ 2 } + 2 t + 3} \right ) + \frac { 5 } { 2 } 2 e − y ( sin ( y ) − cos ( y ) ) = − e − t ( t 2 + 2 t + 3 ) + 2 5
یافتن جواب صریح برای این مسئله ممکن نیست، بنابراین باید جواب را بهشکل ضمنی آن بیان کنیم. یافتن بازه اعتبار از جوابهای ضمنی اغلب میتواند بسیار دشوار باشد، بنابراین، در این مسئله نیز از آن صرفنظر میکنیم.
نمونه سوال معادلات دیفرانسیل ۴
معادله دیفرانسیل مرتبه اول زیر را حل کنید.
cos ( x ) y ′ + sin ( x ) y = 2 cos 3 ( x ) sin ( x ) − 1 y ( π 4 ) = 3 2 , 0 ≤ x < π 2 \cos \left ( x \right ) y' + \sin \left ( x \right ) y = 2 { \cos ^ 3 } \left ( x \right ) \sin \left ( x \right ) - 1 \hspace{0.25in} y \left ( { \frac { \pi } { 4 } } \right ) = 3 \sqrt 2 ,\hspace {0.25in} \, \,\,\,\,\,0 \le x < \frac { \pi } { 2 } cos ( x ) y ′ + sin ( x ) y = 2 cos 3 ( x ) sin ( x ) − 1 y ( 4 π ) = 3 2 , 0 ≤ x < 2 π
حل سوال ۴: معادله دیفرانسیل را بازنویسی میکنیم تا ضریب را بهدست آوریم:
y ′ + sin ( x ) cos ( x ) y = 2 cos 2 ( x ) sin ( x ) − 1 cos ( x ) y ′ + tan ( x ) y = 2 cos 2 ( x ) sin ( x ) − sec ( x ) \begin {align*} y' + \frac { { \sin \left ( x \right ) } } { { \cos \left ( x \right ) } } y & = 2 { \cos ^ 2 } \left ( x \right ) \sin \left ( x \right ) - \frac { 1 } { { \cos \left ( x \right ) } } \\ y' + \tan \left ( x \right ) y & = 2 { \cos ^ 2 } \left ( x \right ) \sin \left ( x \right ) - \sec \left ( x \right ) \end {align*} y ′ + cos ( x ) sin ( x ) y y ′ + tan ( x ) y = 2 cos 2 ( x ) sin ( x ) − cos ( x ) 1 = 2 cos 2 ( x ) sin ( x ) − sec ( x )
اکنون عامل انتگرالساز را محاسبه میکنیم:
μ ( t ) = e ∫ tan ( x ) d x = e ln ∣ sec ( x ) ∣ = e ln sec ( x ) = sec ( x ) \mu \left ( t \right ) = { { \bf { e } } ^ { \int { { \tan \left ( x \right ) \, d x } } } } = { { \bf { e } } ^ { \ln \left | { \sec \left ( x \right ) } \right | } } = { { \bf { e } } ^ { \ln \, \, \sec \left ( x \right ) } } = \sec \left ( x \right ) μ ( t ) = e ∫ t a n ( x ) d x = e l n ∣ s e c ( x ) ∣ = e l n s e c ( x ) = sec ( x )
اکنون عامل انتگرالساز را در معادله دیفرانسیل ضرب میکنیم. توجه داشته باشید که عامل انتگرالساز را در معادله دیفرانسیل بازنویسی شده ضرب میکنیم و نه معادله دیفرانسیل اصلی. مطمئن شوید که این کار را انجام میدهید. اگر عامل انتگرالساز را در معادله دیفرانسیل اصلی ضرب کنید، به جواب اشتباهی خواهید رسید.
sec ( x ) y ′ + sec ( x ) tan ( x ) y = 2 sec ( x ) cos 2 ( x ) sin ( x ) − sec 2 ( x ) ( sec ( x ) y ) ′ = 2 cos ( x ) sin ( x ) − sec 2 ( x ) \begin {align*} \sec \left ( x \right ) y' + \sec \left ( x \right ) \tan \left ( x \right ) y & = 2 \sec \left ( x \right ) { \cos ^ 2 } \left ( x \right ) \sin \left ( x \right ) - { \sec ^ 2 } \left ( x \right ) \\ { \left ( { \sec \left ( x \right ) y } \right ) ^ \prime } & = 2 \cos \left ( x \right ) \sin \left ( x \right ) - { \sec ^ 2 } \left ( x \right ) \end {align*} sec ( x ) y ′ + sec ( x ) tan ( x ) y ( sec ( x ) y ) ′ = 2 sec ( x ) cos 2 ( x ) sin ( x ) − sec 2 ( x ) = 2 cos ( x ) sin ( x ) − sec 2 ( x )
اکنون از دو طرف انتگرال میگیرم:
∫ ( sec ( x ) y ( x ) ) ′ d x = ∫ 2 cos ( x ) sin ( x ) − sec 2 ( x ) d x sec ( x ) y ( x ) = ∫ sin ( 2 x ) − sec 2 ( x ) d x sec ( x ) y ( x ) = − 1 2 cos ( 2 x ) − tan ( x ) + c \begin {align*} \int { { { { \left ( { \sec \left ( x \right ) y \left ( x \right ) } \right ) } ^ \prime } \, d x } } & = \int { { 2 \cos \left ( x \right ) \sin \left ( x \right ) - { { \sec } ^ 2 } \left ( x \right ) \, d x } } \\ \sec \left ( x \right ) y \left ( x \right ) & = \int { { \sin \left ( { 2 x } \right ) - { { \sec } ^ 2 } \left ( x \right ) \, d x } } \\ \sec \left ( x \right ) y \left ( x \right ) & = - \frac { 1 } { 2 } \cos \left ( { 2 x } \right ) - \tan \left ( x \right ) + c \end {align*} ∫ ( sec ( x ) y ( x ) ) ′ d x sec ( x ) y ( x ) sec ( x ) y ( x ) = ∫ 2 cos ( x ) sin ( x ) − sec 2 ( x ) d x = ∫ sin ( 2 x ) − sec 2 ( x ) d x = − 2 1 cos ( 2 x ) − tan ( x ) + c
از اتحاد مثلثاتی sin ( 2 θ ) = 2 sin θ cos θ \sin \left( {2\theta } \right) = 2\sin \theta \cos \theta sin ( 2 θ ) = 2 sin θ cos θ
y ( x ) = − 1 2 cos ( x ) cos ( 2 x ) − cos ( x ) tan ( x ) + c cos ( x ) = − 1 2 cos ( x ) cos ( 2 x ) − sin ( x ) + c cos ( x ) \begin {align*} y \left ( x \right ) & = - \frac { 1 } { 2 } \cos \left ( x \right ) \cos \left ( { 2 x } \right ) - \cos \left ( x \right ) \tan \left ( x \right ) + c \cos \left ( x \right ) \\ & = - \frac { 1 } { 2 } \cos \left ( x \right ) \cos \left ( { 2 x } \right ) - \sin \left ( x \right ) + c \cos \left ( x \right ) \end {align*} y ( x ) = − 2 1 cos ( x ) cos ( 2 x ) − cos ( x ) tan ( x ) + c cos ( x ) = − 2 1 cos ( x ) cos ( 2 x ) − sin ( x ) + c cos ( x )
در نهایت، مقدار ثابت c c c
3 2 = y ( π 4 ) = − 1 2 cos ( π 4 ) cos ( π 2 ) − sin ( π 4 ) + c cos ( π 4 ) 3 2 = − 2 2 + c 2 2 c = 7 \begin {align*} 3 \sqrt 2 = y \left ( { \frac { \pi } { 4 } } \right ) & = - \frac { 1 } { 2 } \cos \left ( { \frac { \pi } { 4 } } \right ) \cos \left ( { \frac { \pi } { 2 } } \right) - \sin \left ( { \frac { \pi } { 4 } } \right ) + c \cos \left ( { \frac { \pi } { 4 } } \right ) \\ 3 \sqrt 2 & = - \frac { { \sqrt 2 } } { 2 } + c \frac { { \sqrt 2 } } { 2 } \\ c & = 7 \end {align*} 3 2 = y ( 4 π ) 3 2 c = − 2 1 cos ( 4 π ) cos ( 2 π ) − sin ( 4 π ) + c cos ( 4 π ) = − 2 2 + c 2 2 = 7
جواب نهایی معادله اینگونه است:
y ( x ) = − 1 2 cos ( x ) cos ( 2 x ) − sin ( x ) + 7 cos ( x ) y \left ( x \right ) = - \frac { 1 } { 2 } \cos \left ( x \right ) \cos \left ( { 2 x } \right ) - \sin \left ( x \right) + 7 \cos \left ( x \right ) y ( x ) = − 2 1 cos ( x ) cos ( 2 x ) − sin ( x ) + 7 cos ( x )
نمودار جواب در شکل زیر نشان داده شده است.
نمونه سوال معادلات دیفرانسیل ۵
معادله دیفرانسیل ( 1 + y 2 ) d x + x y d y = 0 \left( {1 + {y^2}} \right)dx +xydy = 0 ( 1 + y 2 ) d x + x y d y = 0
حل سوال ۵: ابتدا کامل بودن معادله دیفرانسیل را آزمایش میکنیم:
∂ Q ∂ x = ∂ ∂ x ( x y ) = y , ∂ P ∂ y = ∂ ∂ y ( 1 + y 2 ) = 2 y . { { \frac { { \partial Q } } { { \partial x } } } = { \frac { \partial } { { \partial x } } \left( { x y } \right) } = { y,\;\;}}\kern0pt { { \frac { { \partial P } } { { \partial y } } } = { \frac { \partial } { { \partial y } } \left( { 1 + { y ^ 2 } } \right) }={ 2 y . } } ∂ x ∂ Q = ∂ x ∂ ( x y ) = y , ∂ y ∂ P = ∂ y ∂ ( 1 + y 2 ) = 2 y .
همانطور که میبینیم، این معادله کامل نیست. بنابراین، عامل انتگرالساز را برای کامل شدن آن پیدا میکنیم.
عبارت زیر را محاسبه میکنیم:
∂ P ∂ y – ∂ Q ∂ x = 2 y – y = y . { \frac { { \partial P } } { { \partial y } } – \frac { { \partial Q } } { { \partial x } } } = { 2 y – y = y . } ∂ y ∂ P – ∂ x ∂ Q = 2 y – y = y .
معادله زیر فقط به متغیر x x x
1 Q ( ∂ P ∂ y – ∂ Q ∂ x ) = 1 x y ⋅ y = 1 x { \frac { 1 } { Q }\left( {\frac { { \partial P } } { { \partial y } } – \frac { { \partial Q } } { { \partial x } } } \right) } = { \frac { 1 } { { x y } } \cdot y } = { \frac{1}{x}} Q 1 ( ∂ y ∂ P – ∂ x ∂ Q ) = x y 1 ⋅ y = x 1
بنابراین، عامل انتگرالساز نیز فقط بر حسب x x x μ = μ ( x ) \mu = \mu \left( x \right) μ = μ ( x )
1 μ d μ d x = 1 x . \frac { 1 } { \mu } \frac { { d \mu } } { { d x } } = \frac { 1 } { x }. μ 1 d x d μ = x 1 .
با جداسازی متغیرها و انتگرالگیری داریم:
∫ d μ μ = ∫ d x x , ⇒ ln ∣ μ ∣ = ln ∣ x ∣ , ⇒ μ = ± x . { \int { \frac { { d \mu } } { \mu } } = \int { \frac { { d x } } { x } } ,\;\;}\Rightarrow {\ln \left| \mu \right| = \ln \left| x \right|,\;\;}\Rightarrow { \mu = \pm x.} ∫ μ d μ = ∫ x d x , ⇒ ln ∣ μ ∣ = ln ∣ x ∣ , ⇒ μ = ± x .
تساوی μ = x \mu = x μ = x μ = x \mu = x μ = x
( x + x y 2 ) d x + x 2 y d y = 0. \left( {x + x { y ^ 2 } } \right) d x + { x ^ 2 } y d y = 0. ( x + x y 2 ) d x + x 2 y d y = 0.
در واقع، اکنون داریم:
∂ Q ∂ x = ∂ ∂ x ( x 2 y ) = 2 x y = ∂ P ∂ y = ∂ ∂ y ( x + x y 2 ) = 2 x y . { \frac { { \partial Q } } { { \partial x } } = \frac { \partial } { { \partial x } } \left( { { x ^ 2 } y } \right) } = { 2 x y } = { \frac { { \partial P } } { { \partial y } } } = { \frac { \partial } { { \partial y } } \left( { x + x { y ^ 2 } } \right) }={ 2 x y . } ∂ x ∂ Q = ∂ x ∂ ( x 2 y ) = 2 x y = ∂ y ∂ P = ∂ y ∂ ( x + x y 2 ) = 2 x y .
معادله حاصل را حل میکنیم. تابع u ( x , y ) u\left( {x,y} \right) u ( x , y )
{ ∂ u ∂ x = x + x y 2 ∂ u ∂ y = x 2 y . \left\{ \begin{array}{l} \frac{{\partial u}}{{\partial x}} = x + x{y^2}\\ \frac{{\partial u}}{{\partial y}} = {x^2}y \end{array} \right.. { ∂ x ∂ u = x + x y 2 ∂ y ∂ u = x 2 y .
از معادله اول میتوان نوشت:
u ( x , y ) = ∫ ( x + x y 2 ) d x = x 2 2 + x 2 y 2 2 + φ ( y ) . {u\left( {x,y} \right) = \int {\left( {x + x{y^2}} \right)dx} }={ \frac{{{x^2}}}{2} + \frac{{{x^2}{y^2}}}{2} + \varphi \left( y \right).} u ( x , y ) = ∫ ( x + x y 2 ) d x = 2 x 2 + 2 x 2 y 2 + φ ( y ) .
با جایگذاری این معادله در معادله دوم، میتوانیم φ ( y ) \varphi \left( y \right) φ ( y )
∂ u ∂ y = ∂ ∂ y [ x 2 2 + x 2 y 2 2 + φ ( y ) ] = x 2 y , ⇒ x 2 y + φ ’ ( y ) = x 2 y , ⇒ φ ’ ( y ) = 0. {{\frac{{\partial u}}{{\partial y}} }={ \frac{\partial }{{\partial y}}\left[ {\frac{{{x^2}}}{2} + \frac{{{x^2}{y^2}}}{2} + \varphi \left( y \right)} \right] }={ {x^2}y,\;\;}} \\ \Rightarrow { {x^2}y + \varphi’\left( y \right) = {x^2}y,\;\;}\Rightarrow { \varphi’\left( y \right) = 0.} ∂ y ∂ u = ∂ y ∂ [ 2 x 2 + 2 x 2 y 2 + φ ( y ) ] = x 2 y , ⇒ x 2 y + φ ’ ( y ) = x 2 y , ⇒ φ ’ ( y ) = 0.
از معادله بالا φ ( y ) = C \varphi \left( y \right) = C φ ( y ) = C C C C
بنابراین، جواب عمومی معادله دیفرانسیل اصلی برابر است با:
x 2 2 + x 2 y 2 2 + C = 0. {\frac{{{x^2}}}{2} + \frac{{{x^2}{y^2}}}{2} }+{ C }={ 0.} 2 x 2 + 2 x 2 y 2 + C = 0.
نمونه سوال معادلات دیفرانسیل ۶
جواب معادله دیفرانسیل زیر را بیابید.
t y ′ − 2 y = t 5 sin ( 2 t ) − t 3 + 4 t 4 y ( π ) = 3 2 π 4 t \, y' - 2 y = { t ^ 5 } \sin \left ( { 2 t } \right ) - { t ^ 3 } + 4 { t ^ 4 } \hspace {0.25in} y \left ( \pi \right ) = \frac { 3 } { 2 } { \pi ^ 4 } t y ′ − 2 y = t 5 sin ( 2 t ) − t 3 + 4 t 4 y ( π ) = 2 3 π 4
حل سوال ۶: ابتدا دو طرف معادله را بر t t t
y ′ − 2 t y = t 4 sin ( 2 t ) − t 2 + 4 t 3 y' - \frac { 2 } { t } y = { t ^ 4 } \sin \left ( { 2 t } \right ) - { t ^ 2 } + 4 { t ^ 3 } y ′ − t 2 y = t 4 sin ( 2 t ) − t 2 + 4 t 3
اکنون میتوانیم عامل انتگرالساز را محاسبه کنیم:
μ ( t ) = e ∫ − 2 t d t = e − 2 ln ∣ t ∣ \mu \left ( t \right ) = { { \bf { e } } ^ { \int { { - \frac { 2 } { t } d t } } } } = { { \bf { e } } ^ { - 2 \ln \left | { \, t } \right | } } μ ( t ) = e ∫ − t 2 d t = e − 2 l n ∣ t ∣
μ ( t ) = e − 2 ln ∣ t ∣ = e ln ∣ t ∣ − 2 = ∣ t ∣ − 2 = t − 2 \mu \left ( t \right ) = { { \bf { e } } ^ { - 2 \ln \left | { \, t } \right | } } = { { \bf { e } } ^ { \ln { { \left | { \, t } \right | } ^ { \, - \, 2 } } } } = { \left | t \right | ^ { - 2 } } = { t ^ { - 2 } } μ ( t ) = e − 2 l n ∣ t ∣ = e l n ∣ t ∣ − 2 = ∣ t ∣ − 2 = t − 2
اکنون، عامل انتگرالساز را در معادله بازنویسیشده ضرب میکنیم:
( t − 2 y ) ′ = t 2 sin ( 2 t ) − 1 + 4 t { \left ( { { t ^ { - 2 } } y } \right ) ^ \prime } = { t ^ 2 } \sin \left ( { 2 t } \right ) - 1 + 4 t ( t − 2 y ) ′ = t 2 sin ( 2 t ) − 1 + 4 t
برای بهدست آوردن جواب، از دو طرف معادله انتگرال میگیریم:
t − 2 y ( t ) = ∫ t 2 sin ( 2 t ) d t + ∫ − 1 + 4 t d t t − 2 y ( t ) = − 1 2 t 2 cos ( 2 t ) + 1 2 t sin ( 2 t ) + 1 4 cos ( 2 t ) − t + 2 t 2 + c y ( t ) = − 1 2 t 4 cos ( 2 t ) + 1 2 t 3 sin ( 2 t ) + 1 4 t 2 cos ( 2 t ) − t 3 + 2 t 4 + c t 2 \begin {align*} { t ^ { - 2 } } y \left ( t \right ) & = \int { { { t ^ 2 } \sin \left ( { 2 t } \right ) \, d t } } + \int { { - 1 + 4 t \, d t } } \\ { t ^ { - 2 } } y \left ( t \right ) & = - \frac { 1 } { 2 } { t ^ 2 } \cos \left ( { 2 t } \right ) + \frac { 1 }{ 2 } t \sin \left ( { 2 t } \right ) + \frac { 1 } { 4 } \cos \left ( { 2 t } \right ) - t + 2 { t ^ 2 } + c \\ y \left ( t \right ) & = - \frac { 1 } { 2 } { t ^ 4 } \cos \left ( { 2 t } \right ) + \frac { 1 } { 2 } { t ^ 3 } \sin \left ( { 2 t } \right ) + \frac { 1 } { 4 } { t ^ 2 } \cos \left ( { 2 t } \right ) - { t ^ 3 } + 2 { t ^ 4 } + c { t ^ 2 } \end {align*} t − 2 y ( t ) t − 2 y ( t ) y ( t ) = ∫ t 2 sin ( 2 t ) d t + ∫ − 1 + 4 t d t = − 2 1 t 2 cos ( 2 t ) + 2 1 t sin ( 2 t ) + 4 1 cos ( 2 t ) − t + 2 t 2 + c = − 2 1 t 4 cos ( 2 t ) + 2 1 t 3 sin ( 2 t ) + 4 1 t 2 cos ( 2 t ) − t 3 + 2 t 4 + c t 2
اکنون با استفاده از شرایط اولیه مقدار ثابت c c c
y ( t ) = − 1 2 t 4 cos ( 2 t ) + 1 2 t 3 sin ( 2 t ) + 1 4 t 2 cos ( 2 t ) − t 3 + 2 t 4 + ( π − 1 4 ) t 2 y \left ( t \right ) = - \frac { 1 } { 2 } { t ^ 4 } \cos \left ( { 2 t } \right ) + \frac { 1 } { 2 } { t ^ 3 } \sin \left ( { 2 t } \right ) + \frac { 1} { 4 } { t ^ 2 } \cos \left ( { 2 t } \right ) - { t ^ 3 } + 2 { t ^ 4 } + \left ( {\pi - \frac { 1 } { 4 } } \right ) { t ^ 2 } y ( t ) = − 2 1 t 4 cos ( 2 t ) + 2 1 t 3 sin ( 2 t ) + 4 1 t 2 cos ( 2 t ) − t 3 + 2 t 4 + ( π − 4 1 ) t 2
شکل زیر، نمودار جواب را نشان میدهد.
معادله دیفرانسیل y ′ ′ = 1 4 y y^{\prime\prime} = {\frac{1}{{4\sqrt y }}\normalsize} y ′′ = 4 y 1
نمونه سوال معادلات دیفرانسیل ۷
معادله دیفرانسیل زیر را با شرط اولیه y ( 1 ) = 1 y\left( 1 \right) = 1 y ( 1 ) = 1
1 y 2 – 2 x = 2 x y ’ y 3 {\frac{1}{{{y^2}}}\normalsize} – {\frac{2}{x}\normalsize} ={\frac{{2xy’}}{{{y^3}}}\normalsize} y 2 1 – x 2 = y 3 2 x y ’
حل سوال ۷: ابتدا معادله را بهفرم استاندارد مینویسیم:
1 y 2 – 2 x = 2 x y 3 d y d x , ⇒ ( 1 y 2 – 2 x ) d x = 2 x y 3 d y , ⇒ ( 1 y 2 – 2 x ) d x – 2 x y 3 d y = 0. {\frac{1}{{{y^2}}} – \frac{2}{x} = \frac{{2x}}{{{y^3}}}\frac{{dy}}{{dx}},\;\;}\\ \Rightarrow {\left( {\frac{1}{{{y^2}}} – \frac{2}{x}} \right)dx = \frac{{2x}}{{{y^3}}}dy,\;\;}\\ \Rightarrow {\left( {\frac{1}{{{y^2}}} – \frac{2}{x}} \right)dx – \frac{{2x}}{{{y^3}}}dy }={ 0.} y 2 1 – x 2 = y 3 2 x d x d y , ⇒ ( y 2 1 – x 2 ) d x = y 3 2 x d y , ⇒ ( y 2 1 – x 2 ) d x – y 3 2 x d y = 0.
مشتقات جزئی مربوط به آزمون کامل بوده، بهصورت زیر هستند:
∂ Q ∂ x = ∂ ∂ x ( – 2 x y 3 ) = – 2 y 3 , ∂ P ∂ y = ∂ ∂ y ( 1 y 2 – 2 x ) = – 2 y 3 . {{\frac{{\partial Q}}{{\partial x}} }={ \frac{\partial }{{\partial x}}\left( { – \frac{{2x}}{{{y^3}}}} \right) }={ – \frac{2}{{{y^3}}},\;\;\;}}\kern-0.3pt {{\frac{{\partial P}}{{\partial y}} }={ \frac{\partial }{{\partial y}}\left( {\frac{1}{{{y^2}}} – \frac{2}{x}} \right) }={ – \frac{2}{{{y^3}}}.}} ∂ x ∂ Q = ∂ x ∂ ( – y 3 2 x ) = – y 3 2 , ∂ y ∂ P = ∂ y ∂ ( y 2 1 – x 2 ) = – y 3 2 .
در نتیجه، معادله کامل است. اکنون دستگاه معادلات زیر را برای یافتن تابع u ( x , y ) u\left( {x,y} \right) u ( x , y )
{ ∂ u ∂ x = 1 y 2 – 2 x ∂ u ∂ y = – 2 x y 3 . \left\{ \begin{array}{l} \frac{{\partial u}}{{\partial x}} = \frac{1}{{{y^2}}} – \frac{2}{x}\\ \frac{{\partial u}}{{\partial y}} = – \frac{{2x}}{{{y^3}}} \end{array} \right.. { ∂ x ∂ u = y 2 1 – x 2 ∂ y ∂ u = – y 3 2 x .
در ادامه، با انتگرالگیری از معادله دوم نسبت y y y
u ( x , y ) = ∫ ( – 2 x y 3 ) d y = x y 2 + ψ ( x ) . {u\left( {x,y} \right) }={ \int {\left( { – \frac{{2x}}{{{y^3}}}} \right)dy} } = {\frac{x}{{{y^2}}} + \psi \left( x \right).} u ( x , y ) = ∫ ( – y 3 2 x ) d y = y 2 x + ψ ( x ) .
با مشتقگیری از معادله اخیر نسبت به متغیر x x x
$$\require {cancel} {{\frac{{\partial u}}{{\partial x}} }={ \frac{\partial }{{\partial x}}\left[ {\frac{x}{{{y^2}}} + \psi \left( x \right)} \right] }={ \frac{1}{{{y^2}}} – \frac{2}{x},\;\;}}\\ \Rightarrow<br />
{{\cancel{\frac{1}{{{y^2}}}} + \psi’\left( x \right) }={ \cancel{\frac{1}{{{y^2}}}} – \frac{2}{x},\;\;}}\\ \Rightarrow<br />
{\psi’\left( x \right) = – \frac{2}{x},\;\;}\Rightarrow<br />
{{\psi \left( x \right) = – 2\ln \left| x \right| }={ \ln \frac{1}{{{x^2}}}.}}$$
در نهایت، جواب عمومی معادله دیفرانسیل، بهفرم ضمنی زیر بهدست میآید:
x y 2 + ln 1 x 2 = C . \frac{x}{{{y^2}}} + \ln \frac{1}{{{x^2}}} = C. y 2 x + ln x 2 1 = C .
جواب خصوصی را نیز میتوان با استفاده از شرط اولیه y ( 1 ) = 1 y\left( 1 \right) = 1 y ( 1 ) = 1 C C C
1 1 2 + ln 1 1 2 = C , ⇒ 1 + 0 = C , ⇒ C = 1. {\frac{1}{{{1^2}}} + \ln \frac{1}{{{1^2}}} = C,\;\;}\Rightarrow {1 + 0 = C,\;\;}\Rightarrow {C = 1.} 1 2 1 + ln 1 2 1 = C , ⇒ 1 + 0 = C , ⇒ C = 1.
بنابراین، جواب نهایی با در نظر گرفتن شرایط اولیه، بهصورت زیر است:
1 y 2 + ln 1 x 2 = 1. \frac{1}{{{y^2}}} + \ln \frac{1}{{{x^2}}} = 1. y 2 1 + ln x 2 1 = 1.
نمونه سوال معادلات دیفرانسیل ۸
معادله دیفرانسیل زیر را حل کنید:
e y d x + ( 2 y + x e y ) d y = 0 {e^y}dx +\left( {2y + x{e^y}} \right)dy=0 e y d x + ( 2 y + x e y ) d y = 0
حل سوال ۸: ابتدا کامل بودن معادله را بررسی میکنیم:
∂ Q ∂ x = ∂ ∂ x ( 2 y + x e y ) = e y , ∂ P ∂ y = ∂ ∂ y ( e y ) = e y . {{\frac{{\partial Q}}{{\partial x}} }={ \frac{\partial }{{\partial x}}\left( {2y + x{e^y}} \right) }={ {e^y},\;\;}}\kern-0.3pt {{\frac{{\partial P}}{{\partial y}} }={ \frac{\partial }{{\partial y}}\left( {{e^y}} \right) }={ {e^y}.}} ∂ x ∂ Q = ∂ x ∂ ( 2 y + x e y ) = e y , ∂ y ∂ P = ∂ y ∂ ( e y ) = e y .
میبینیم که تساوی ∂ Q ∂ x = ∂ P ∂ y {\frac{{\partial Q}}{{\partial x}}\normalsize} = {\frac{{\partial P}}{{\partial y}}\normalsize} ∂ x ∂ Q = ∂ y ∂ P u ( x , y ) u\left( {x,y} \right) u ( x , y )
{ ∂ u ∂ x = e y ∂ u ∂ y = 2 y + x e y . \left\{ \begin{array}{l} \frac{{\partial u}}{{\partial x}} = {e^y}\\ \frac{{\partial u}}{{\partial y}} = 2y + x{e^y} \end{array} \right.. { ∂ x ∂ u = e y ∂ y ∂ u = 2 y + x e y .
در نتیجه، داریم:
u ( x , y ) = ∫ P ( x , y ) d x = ∫ e y d x = x e y + φ ( y ) . {u\left( {x,y} \right) = \int {P\left( {x,y} \right)dx} } = {\int {{e^y}dx} }={ x{e^y} + \varphi \left( y \right).} u ( x , y ) = ∫ P ( x , y ) d x = ∫ e y d x = x e y + φ ( y ) .
اکنون، با مشتقگیری از u u u y y y φ ’ ( y ) \varphi’\left( y \right) φ ’ ( y )
$$\require {cancel}{{\frac{{\partial u}}{{\partial y}} }={ \frac{\partial }{{\partial y}}\left[ {x{e^y} + \varphi \left( y \right)} \right] }={ 2y + x{e^y},\;\;}}\\<br />
\Rightarrow<br />
{{\cancel{x{e^y}} + \varphi’\left( y \right) }={ 2y + \cancel{x{e^y}},\;\;}}\\ \Rightarrow<br />
{\varphi’\left( y \right) = 2y.}$$
در نتیجه، تابع φ ( y ) {\varphi \left( y \right)} φ ( y )
φ ( y ) = ∫ 2 y d y = y 2 , ⇒ u ( x , y ) = x e y + φ ( y ) = x e y + y 2 . {\varphi \left( y \right) = \int {2ydy} = {y^2},\;\;}\Rightarrow {u\left( {x,y} \right) = x{e^y} + \varphi \left( y \right) } = {x{e^y} + {y^2}.} φ ( y ) = ∫ 2 y d y = y 2 , ⇒ u ( x , y ) = x e y + φ ( y ) = x e y + y 2 .
در نهایت، پاسخ معادله دیفرانسیل بهصورت زیر است:
x e y + y 2 = C . x{e^y} + {y^2} = C. x e y + y 2 = C .
نمونه سوال معادلات دیفرانسیل ۹
معادله دیفرانسیل زیر را حل کنید.
2 x y 2 + 4 = 2 ( 3 − x 2 y ) y ′ y ( − 1 ) = 8 2x{y^2} + 4 = 2\left( {3 - {x^2}y} \right)y'\hspace{0.25in}y\left( { - 1} \right) = 8 2 x y 2 + 4 = 2 ( 3 − x 2 y ) y ′ y ( − 1 ) = 8
حل سوال ۹: ابتدا باید معادله دیفرانسیل را در شکل مناسب قرار دهیم. به یاد داشته باشید که یک طرف معادله باید برابر با 0 0 0
2 x y 2 + 4 − 2 ( 3 − x 2 y ) y ′ = 0 2 x y 2 + 4 + 2 ( x 2 y − 3 ) y ′ = 0 \begin{align*} 2 x { y ^ 2 } + 4 - 2\left ( { 3 - { x ^ 2 } y } \right ) y' & = 0 \\ 2 x { y ^ 2 } + 4 + 2 \left ( { { x ^ 2 } y - 3 } \right ) y' & = 0 \end {align*} 2 x y 2 + 4 − 2 ( 3 − x 2 y ) y ′ 2 x y 2 + 4 + 2 ( x 2 y − 3 ) y ′ = 0 = 0
اکنون، خواهیم داشت:
M = 2 x y 2 + 4 M y = 4 x y N = 2 x 2 y − 6 N x = 4 x y \begin {align*} M & = 2 x { y ^ 2 } + 4 \hspace{0.25in} { M _ y } = 4 x y \\ N & = 2 { x ^ 2 } y - 6 \hspace{0.25in} { N _ x } = 4 x y \end {align*} M N = 2 x y 2 + 4 M y = 4 x y = 2 x 2 y − 6 N x = 4 x y
و بنابراین معادله دیفرانسیل کامل است. میتوانیم از M M M x x x N N N y y y N N N
Ψ ( x , y ) = ∫ 2 x 2 y − 6 d y = x 2 y 2 − 6 y + h ( x ) \Psi \left ( { x , y } \right ) = \int { { 2 { x ^ 2 } y - 6 \, d y } } = { x ^ 2 } { y ^ 2 } - 6 y + h \left ( x \right ) Ψ ( x , y ) = ∫ 2 x 2 y − 6 d y = x 2 y 2 − 6 y + h ( x )
دقت کنید که ثابت انتگرالگیری تابعی از x x x y y y x x x M M M
Ψ x = 2 x y 2 + h ′ ( x ) = 2 x y 2 + 4 = M { \Psi _ x } = 2 x { y ^ 2 } + h' \left ( x \right ) = 2 x { y ^ 2 } + 4 = M Ψ x = 2 x y 2 + h ′ ( x ) = 2 x y 2 + 4 = M
در نتیجه، خواهیم داشت:
h ′ ( x ) = 4 ⇒ h ( x ) = 4 x h' \left ( x \right ) = 4 \hspace {0.25in} \Rightarrow \hspace{0.25in}\,\,\,h\left( x \right ) = 4 x h ′ ( x ) = 4 ⇒ h ( x ) = 4 x
بنابراین، Ψ ( x , y ) \Psi\left(x,y\right) Ψ ( x , y )
Ψ ( x , y ) = x 2 y 2 − 6 y + 4 x \Psi \left( {x,y} \right) = {x^2}{y^2} - 6y + 4x Ψ ( x , y ) = x 2 y 2 − 6 y + 4 x
در نتیجه، جواب ضمنی معادله دیفرانسیل بهشکل زیر خواهد بود:
x 2 y 2 − 6 y + 4 x = c {x^2}{y^2} - 6y + 4x = c x 2 y 2 − 6 y + 4 x = c
با اعمال شرایط اولیه، مقدار ثابت c c c
64 − 48 − 4 = c , c = 12 64 - 48 - 4 = c,\hspace{0.25in}c = 12 64 − 48 − 4 = c , c = 12
و جواب بهصورت زیر است:
x 2 y 2 − 6 y + 4 x − 12 = 0 {x^2}{y^2} - 6y + 4x - 12 = 0 x 2 y 2 − 6 y + 4 x − 12 = 0
از رابطه بالا، y ( x ) y (x ) y ( x )
y ( x ) = 6 ± 36 − 4 x 2 ( 4 x − 12 ) 2 x 2 = 6 ± 36 + 48 x 2 − 16 x 3 2 x 2 = 6 ± 2 9 + 12 x 2 − 4 x 3 2 x 2 = 3 ± 9 + 12 x 2 − 4 x 3 x 2 \begin {align*} y \left ( x \right ) & = \frac { { 6 \pm \sqrt { 3 6 - 4 { x ^ 2 } \left ( { 4 x - 1 2 } \right ) } } } { { 2 { x ^ 2 } } } \\ & = \frac { { 6 \pm \sqrt { 3 6 + 4 8 { x ^ 2 } - 1 6 { x ^ 3 } } } } { { 2 { x ^ 2 } } } \\ & = \frac { { 6 \pm 2 \sqrt { 9 + 1 2 { x ^ 2 } - 4 { x ^ 3 } } } } { { 2 { x ^ 2 } } } \\ & = \frac { { 3 \pm \sqrt { 9 + 1 2 { x ^ 2 } - 4 { x ^ 3 } } } } { { { x ^ 2 } } } \end {align*} y ( x ) = 2 x 2 6 ± 36 − 4 x 2 ( 4 x − 12 ) = 2 x 2 6 ± 36 + 48 x 2 − 16 x 3 = 2 x 2 6 ± 2 9 + 12 x 2 − 4 x 3 = x 2 3 ± 9 + 12 x 2 − 4 x 3
با اعمال دوباره شرایط اولیه، میبینیم که رادیکال مثبت قابل قبول است و جواب صریح معادله بهشکل نهایی زیر خواهد بود:
y ( x ) = 3 + 9 + 12 x 2 − 4 x 3 x 2 y \left ( x \right ) = \frac { { 3 + \sqrt { 9 + 1 2 { x ^ 2 } - 4 { x ^ 3 } } } } { { { x ^ 2 } } } y ( x ) = x 2 3 + 9 + 12 x 2 − 4 x 3
اکنون باید دامنه اعتبار جواب را پیدا کنیم. این دامنه شامل x x x − 4 x 3 + 12 x 2 + 9 > 0 - 4{x^3} + 12{x^2} + 9>0 − 4 x 3 + 12 x 2 + 9 > 0
− ∞ < x < 0 - \infty < x < 0 − ∞ < x < 0
نمودار جواب بهشکل زیر است.
نمونه سوال معادلات دیفرانسیل ۱۰
معادله دیفرانسیل زیر را حل کنید.
y ′ + y x = y 2 y' + \frac { y } { x } = { y ^ 2 } y ′ + x y = y 2
حل سوال ۱۰: این معادله یک معادله برنولی است و از تغییر متغیر زیر برای حل آن استفاده میکنیم:
z = y 1 − m = 1 y z = {y^{1 - m}} = \frac{1}{y} z = y 1 − m = y 1
با مشتقگیری از معادله بالا، داریم:
z ′ = ( 1 y ) ′ = − y ′ y 2 z' = { \left ( { \frac { 1 } { y } } \right ) ^ \prime } = - \frac { { y' } } { {{ y^ 2 } } } z ′ = ( y 1 ) ′ = − y 2 y ′
اکنون، معادله اصلی را بر y 2 y^ 2 y 2
y ′ y 2 + 1 y x = 1 \frac { { y' } } { { { y ^ 2 } } } + \frac { 1 } { { y x } } = 1 y 2 y ′ + y x 1 = 1
با این کار، جواب y = 0 y = 0 y = 0
اکنون معادله را برحسب z z z
z ′ − z x = − 1 z' - \frac { z } { x } = - 1 z ′ − x z = − 1
اکنون یک معادله خطی برای تابع z ( x ) z ( x ) z ( x )
u ( x ) = e ∫ ( − 1 x ) d x = e − ∫ d x x = e − ln ∣ x ∣ = e ln 1 ∣ x ∣ = 1 ∣ x ∣ u \left ( x \right ) = { e ^ { \int { \left ( { - \frac { 1 } { x } } \right ) d x } } } = e ^ { - \int { \frac { { d x } } { x } } } = { e ^ { - \ln \left | x \right | } } = { e ^ { \ln \frac { 1 } { { \left | x \right | } } } } = \frac { 1 } { { \left | x \right | } } u ( x ) = e ∫ ( − x 1 ) d x = e − ∫ x d x = e − l n ∣ x ∣ = e l n ∣ x ∣ 1 = ∣ x ∣ 1
بنابراین، 1 x \frac 1 x x 1
z ′ ⋅ 1 x − z x ⋅ 1 x = z ′ ⋅ 1 x − z x 2 = ( z ⋅ 1 x ) ′ z' \cdot \frac { 1 } { x } - \frac { z } { x } \cdot \frac { 1 } { x } = z' \cdot \frac { 1 } { x } - \frac { z } { { { x ^ 2 } } } = { \left ( {z \cdot \frac { 1 } { x } } \right ) ^ \prime } z ′ ⋅ x 1 − x z ⋅ x 1 = z ′ ⋅ x 1 − x 2 z = ( z ⋅ x 1 ) ′
میبینیم که بعد از ضرب 1 x \frac 1 x x 1 z ( x ) u ( x ) z ( x ) u ( x ) z ( x ) u ( x )
در نتیجه، جواب عمومی معادله خطی برای بهصورت زیر خواهد بود:
z = ∫ u ( x ) f ( x ) d x + C u ( x ) = ∫ 1 x ⋅ ( − 1 ) d x + C 1 x = − ln ∣ x ∣ + C 1 x = x ( C − ln ∣ x ∣ ) z = \frac { { \int { u \left ( x \right ) f \left ( x \right ) d x } + C } } { { u \left ( x \right ) } } = \frac { { \int { \frac { 1 } { x } \cdot \left ( { - 1 } \right ) d x } + C } } { { \frac { 1 } { x } } } = \frac { { - \ln \left | x \right | + C } } { { \frac { 1 } { x } } } = x \left ( { C - \ln \left | x \right | } \right ) z = u ( x ) ∫ u ( x ) f ( x ) d x + C = x 1 ∫ x 1 ⋅ ( − 1 ) d x + C = x 1 − ln ∣ x ∣ + C = x ( C − ln ∣ x ∣ )
با قرار دادن y = 1 z y = \frac{1}{z} y = z 1
y = 1 x ( C − ln ∣ x ∣ ) y = \frac { 1 } { { x \left ( { C - \ln \left | x \right | } \right ) } } y = x ( C − ln ∣ x ∣ ) 1
یا بهفرم ضمنی، جواب بهصورت زیر است:
y x ( C − ln ∣ x ∣ ) = 1 yx\left( {C - \ln \left| x \right|} \right) = 1 y x ( C − ln ∣ x ∣ ) = 1
در نهایت، جواب معادله دیفرانسیل را با در نظر گرفتن جواب ازدسترفته y = 0 y = 0 y = 0
y x ( C − ln ∣ x ∣ ) = 1 , y = 0 y x \left ( { C - \ln \left | x \right | } \right ) = 1,\;\; y = 0 y x ( C − ln ∣ x ∣ ) = 1 , y = 0
نمونه سوال معادلات دیفرانسیل ۱۱
معادله دیفرانسیل زیر را حل کنید.
4 x y y ′ = y 2 + x 2 , y ( 1 ) = 1 4xyy' = {y^2} + {x^2} , \;\;\; y\left( 1 \right) = 1 4 x y y ′ = y 2 + x 2 , y ( 1 ) = 1
حل سوال ۱۱: ابتدا معادله را بهشکل زیر بازنویسی میکنیم:
4 x y y ′ = y 2 + x 2 , ⇒ 4 x y y ′ 4 x y − y 2 4 x y = x 2 4 x y , ⇒ y ′ − y 4 x = x 4 y 4 x y y' = { y ^ 2 } + { x ^ 2 } , \; \; \Rightarrow \frac { { 4 x y y' } } { { 4 x y } } - \frac { { { y ^ 2 } } } { { 4 x y } } = \frac { { { x ^ 2 } } } { { 4 x y } } , \; \; \Rightarrow y' - \frac { y } { { 4 x } } = \frac { x } { { 4 y } } 4 x y y ′ = y 2 + x 2 , ⇒ 4 x y 4 x y y ′ − 4 x y y 2 = 4 x y x 2 , ⇒ y ′ − 4 x y = 4 y x
این معادله یک معادله برنولی است و برای حل آن، میتوانیم از تغییر متغیر z = y 1 − ( − 1 ) = y 2 z = y ^ {1-(-1)} = y ^ 2 z = y 1 − ( − 1 ) = y 2 z ′ = 2 y y ′ z' = 2 y y' z ′ = 2 y y ′ 2 y 2 y 2 y
2 y y ′ − 2 y 2 4 x = 2 x y 4 y , ⇒ 2 y y ′ − y 2 2 x = x 2 2 y y' - \frac { { 2{ y ^2 } } } { { 4 x } } = \frac { { 2 x y } }{ { 4 y } } , \;\; \Rightarrow 2 y y' - \frac { { { y ^ 2 } } }{ { 2 x } } = \frac { x } { 2 } 2 y y ′ − 4 x 2 y 2 = 4 y 2 x y , ⇒ 2 y y ′ − 2 x y 2 = 2 x
با قرار دادن z z z y y y
z ′ − z 2 x = x 2 z' - \frac { z } { { 2 x } } = \frac { x } { 2 } z ′ − 2 x z = 2 x
اکنون عامل انتگرالساز را محاسبه میکنیم:
u ( x ) = e ∫ ( − 1 2 x ) d x = e − 1 2 ∫ d x x = e − 1 2 ln ∣ x ∣ = e ln 1 ∣ x ∣ = 1 ∣ x ∣ u \left ( x \right ) = { e ^ { \int { \left ( { - \frac { 1 } { { 2 x } } } \right ) d x } } } = { e ^ { - \frac { 1 } { 2 } \int { \frac { { d x } } { x } } } } = { e ^ { - \frac { 1 } { 2 } \ln \left | x \right | } } = { e ^ { \ln \frac { 1 } { { \sqrt { \left | x \right | } } } } } = \frac { 1 } { { \sqrt { \left | x \right | } } } u ( x ) = e ∫ ( − 2 x 1 ) d x = e − 2 1 ∫ x d x = e − 2 1 l n ∣ x ∣ = e l n ∣ x ∣ 1 = ∣ x ∣ 1
تابع u ( x ) = 1 x u\left( x \right) = \frac{1}{{\sqrt x }} u ( x ) = x 1 u ( x ) u ( x ) u ( x ) z ( x ) u ( x ) z\left( x \right)u\left( x \right) z ( x ) u ( x )
( z ′ − z 2 x ) u ( x ) = z ′ ⋅ 1 x − z 2 x ⋅ 1 x = z ′ ⋅ 1 x − z ⋅ 1 2 x 3 2 = z ′ ⋅ 1 x − z ⋅ x − 3 2 2 = z ′ ⋅ 1 x + z ⋅ ( x − 1 2 ) ′ = z ′ ⋅ 1 x + z ⋅ ( 1 x ) ′ = ( z ⋅ 1 x ) ′ \begin {align} \left( {z^\prime - \frac{z}{{2x}}} \right)u\left( x \right) & = z^\prime \cdot \frac{1}{{\sqrt x }} - \frac{z}{{2x}} \cdot \frac{1}{{\sqrt x }} = z^\prime \cdot \frac{1}{{\sqrt x }} - z \cdot \frac{1}{{2{x^{\frac{3}{2}}}}} \\ &= z^\prime \cdot \frac{1}{{\sqrt x }} - z \cdot \frac{{{x^{ - \frac{3}{2}}}}}{2} = z^\prime \cdot \frac{1}{{\sqrt x }} + z \cdot \left( {{x^{ - \frac{1}{2}}}} \right)^\prime \\ &= z^\prime \cdot \frac{1}{{\sqrt x }} + z \cdot \left( {\frac{1}{{\sqrt x }}} \right)^\prime = \left( {z \cdot \frac{1}{{\sqrt x }}} \right)^\prime \end{align} ( z ′ − 2 x z ) u ( x ) = z ′ ⋅ x 1 − 2 x z ⋅ x 1 = z ′ ⋅ x 1 − z ⋅ 2 x 2 3 1 = z ′ ⋅ x 1 − z ⋅ 2 x − 2 3 = z ′ ⋅ x 1 + z ⋅ ( x − 2 1 ) ′ = z ′ ⋅ x 1 + z ⋅ ( x 1 ) ′ = ( z ⋅ x 1 ) ′
جواب عمومی معادله خطی بهصورت زیر است:
z = ∫ u ( x ) f ( x ) d x + C u ( x ) = ∫ 1 x ⋅ x 2 d x + C 1 x = 1 2 ∫ x d x + C 1 x = x [ 1 2 ⋅ 2 x 3 2 3 + C ] = x 2 3 + C x \begin {align} z & = \frac { { \int { u \left ( x \right ) f \left ( x \right ) d x } + C } } { { u \left ( x \right ) } } = \frac { { \int { \frac { 1 } { { \sqrt x } } \cdot \frac { x } { 2 } d x } + C } } { { \frac { 1 } { { \sqrt x } } } } \\ & = \frac { { \frac { 1 } { 2 } \int { \sqrt x d x } + C } } { { \frac { 1 } { { \sqrt x } } } } = \sqrt x \left [ { \frac { 1 } { 2 } \cdot \frac { { 2 { x ^ { \frac { 3 }{ 2 } } } }} { 3 } + C } \right ] = \frac { { { x ^ 2 } } } { 3 } + C \sqrt x \end {align} z = u ( x ) ∫ u ( x ) f ( x ) d x + C = x 1 ∫ x 1 ⋅ 2 x d x + C = x 1 2 1 ∫ x d x + C = x [ 2 1 ⋅ 3 2 x 2 3 + C ] = 3 x 2 + C x
با در نظر گرفتن z = y 2 z = {y^2} z = y 2
y = ± x 2 3 + C x y = \pm \sqrt { \frac { { { x ^ 2 } } } { 3 } + C \sqrt x } y = ± 3 x 2 + C x
اکنون میتوانیم C C C
y = 1 2 3 + C 1 = 1 3 + C = 1 y = \sqrt { \frac { { { 1 ^ 2 } } } { 3 } + C \sqrt 1 } = \sqrt { \frac { 1} { 3 } + C } = 1 y = 3 1 2 + C 1 = 3 1 + C = 1
که در نتیجه، C = 2 3 C = \frac { 2 } { 3 } C = 3 2
y = x 2 3 + 2 x 3 y = \sqrt { \frac { { { x ^ 2 } } } { 3 } + \frac { { 2 \sqrt x } } { 3 } } y = 3 x 2 + 3 2 x
نمونه سوال معادلات دیفرانسیل ۱۲
جواب معادله دیفرانسیل زیر را بهدست آورید و دامنه اعتبار جواب را مشخص کنید.
y ′ = 5 y + e − 2 x y − 2 y ( 0 ) = 2 y' = 5 y + { { \bf { e } } ^ { - 2 \, x } } { y ^ { - 2 } } \hspace{0.25in}y\left( 0 \right) = 2 y ′ = 5 y + e − 2 x y − 2 y ( 0 ) = 2
حل سوال ۱۲: ابتدا باید دو طرف معادله را در y 2 y ^ 2 y 2
y 2 y ′ − 5 y 3 = e − 2 x {y^2}\,y' - 5{y^3} = {{\bf{e}}^{ - 2\,x}} y 2 y ′ − 5 y 3 = e − 2 x
از تغییر متغیر زیر استفاده میکنیم:
v = y 3 v ′ = 3 y 2 y ′ v = {y^3}\hspace{0.25in}v' = 3{y^2}y' v = y 3 v ′ = 3 y 2 y ′
با قرار دادن متغیر جدید و مشتق آن در معادله، عامل انتگرالساز بهدست میآید:
1 3 v ′ − 5 v = e − 2 x ⇒ v ′ − 15 v = 3 e − 2 x μ ( x ) = e − 15 , x \frac{1}{3}v' - 5v = {{\bf{e}}^{ - 2\,x}}\hspace{0.25in} \Rightarrow \hspace{0.25in}v' - 15v = 3{{\bf{e}}^{ - 2\,x}}\hspace {0.25in}\mu \left ( x \right ) = { { \bf { e } } ^ { - 1 5 \ , x } } 3 1 v ′ − 5 v = e − 2 x ⇒ v ′ − 15 v = 3 e − 2 x μ ( x ) = e − 15 , x
در نتیجه، خواهیم داشت:
v ( x ) = c e 15 x − 3 17 e − 2 x v\left( x \right) = c{{\bf{e}}^{15\,x}} - \frac{3}{{17}}{{\bf{e}}^{ - 2\,x}} v ( x ) = c e 15 x − 17 3 e − 2 x
اکنون جواب را برای y y y
y 3 = c e 15 x − 3 17 e − 2 x {y^3} = c{{\bf{e}}^{15\,x}} - \frac{3}{{17}}{{\bf{e}}^{ - 2\,x}} y 3 = c e 15 x − 17 3 e − 2 x
با اعمال شرایط اولیه، مقدار ثابت c c c
8 = c − 3 17 ⇒ c = 139 17 8 = c - \frac{3}{{17}}\hspace{0.25in} \Rightarrow \hspace{0.25in}c = \frac{{139}}{{17}} 8 = c − 17 3 ⇒ c = 17 139
با قرار دادن c c c
y ( x ) = ( 139 e 15 x − 3 e − 2 x 17 ) 1 3 y \left ( x \right) = { \left ( { \frac { { 1 3 9 { { \bf { e } } ^ { 1 5 \, x } } - 3 { { \bf { e } } ^{ - 2 \, x } } } } { { 1 7 } } } \right ) ^ { \frac { 1 } { 3 } } } y ( x ) = ( 17 139 e 15 x − 3 e − 2 x ) 3 1
این جواب برای همه مقادیر x x x
نمونه سوال معادلات دیفرانسیل ۱۳
معادله دیفرانسیل y ′ = y + y 2 + 1 y ^ { \prime } = y + { y ^ 2 } + 1 y ′ = y + y 2 + 1
حل سوال ۱۳: همانطور که میبینیم، ضرایب این معادله ثابت هستند و پس از جداسازی متغیرهای x x x y y y
d y d x = y + y 2 + 1 , ⇒ ∫ d y y + y 2 + 1 = ∫ d x , { {\frac{{dy}}{{dx}} = y + {y^2} + 1,\;\;}\Rightarrow {\int {\frac{{dy}}{{y + {y^2} + 1}}} = \int {dx} ,\;\;}} d x d y = y + y 2 + 1 , ⇒ ∫ y + y 2 + 1 d y = ∫ d x ,
با انتگرالگیری از طرفین رابطه اخیر، خواهیم داشت:
1 3 2 arctan y + 1 2 3 2 = x + C , ⇒ 2 3 arctan 2 y + 1 3 = x + C { {{\frac{1}{{\frac{{\sqrt 3 }}{2}}}\arctan \frac{{y + \frac{1}{2}}}{{\frac{{\sqrt 3 }}{2}}} }={ x + C,\;\;}}\Rightarrow {{\frac{2}{{\sqrt 3 }}\arctan \frac{{2y + 1}}{{\sqrt 3 }} }={ x + C}}} 2 3 1 arctan 2 3 y + 2 1 = x + C , ⇒ 3 2 arctan 3 2 y + 1 = x + C
نمونه سوال معادلات دیفرانسیل ۱۴
معادله دیفرانسیل زیر را با در نظر گرفتن جواب خصوصی y 1 = 2 y _ 1 = 2 y 1 = 2
d y d x = − 2 − y + y 2 \frac {d y}{d x}=-2-y+y^{2} d x d y = − 2 − y + y 2
حل سوال ۱۴: این معادله یک معادله ریکاتی است. پیش از هر چیز، باید مطمئن شویم y 1 = 2 y_1 = 2 y 1 = 2
z = 1 y − 2 z=\frac{1}{y-2} z = y − 2 1
در نتیجه، داریم:
y = 2 + 1 z y=2+\frac{1}{z} y = 2 + z 1
که مشتق آن بهصورت زیر است:
y ′ = − z ′ z 2 y^{\prime}=-\frac{z^{\prime}}{z^{2}} y ′ = − z 2 z ′
در نتیجه، معادله بهصورت زیر درمیآید:
− z ′ z 2 = − 2 − ( 2 + 1 z ) + ( 2 + 1 z ) 2 -\frac{z^{\prime}}{z^{2}}=-2-\left(2+\frac{1}{z}\right)+\left(2+\frac{1}{z}\right)^{2} − z 2 z ′ = − 2 − ( 2 + z 1 ) + ( 2 + z 1 ) 2
با کمی عملیات جبری، خواهیم داشت:
− z ′ z 2 = 3 z + 1 z 2 -\frac{z^{\prime}}{z^{2}}=\frac{3}{z}+\frac{1}{z^{2}} − z 2 z ′ = z 3 + z 2 1
بنابراین، داریم:
z ′ = − 3 z − 1 z'=-3z-1 z ′ = − 3 z − 1
این معادله یک معادله خطی است که جواب عمومی آن بهصورت زیر است:
z = − 1 / 3 e 3 x + C e 3 x = − 1 3 + C e − 3 x z=\frac{-1 / 3 e^{3 x}+C}{e^{3 x}}=-\frac{1}{3}+C e^{-3 x} z = e 3 x − 1/3 e 3 x + C = − 3 1 + C e − 3 x
بنابراین، خواهیم داشت:
y = 2 + 1 − 1 3 + C e − 3 x y=2+\frac{1}{-\frac{1}{3}+C e^{-3 x}} y = 2 + − 3 1 + C e − 3 x 1
نمونه سوال معادلات دیفرانسیل ۱۵
معادله دیفرانسیل زیر را با در نظر گرفتن شرایط اولیه y ( 0 ) = − 1 y (0)=-1 y ( 0 ) = − 1 y 1 = sin ( x ) y_1=\sin (x) y 1 = sin ( x )
d y d x = − 2 − y + y 2 \frac {d y}{d x}=-2-y+y^{2} d x d y = − 2 − y + y 2
حل سوال ۱۵: ابتدا بررسی میکنیم که y 1 = sin ( x ) y _ 1 = \sin (x ) y 1 = sin ( x )
d y d x = 2 cos 2 ( x ) − sin 2 ( x ) + y 2 2 cos ( x ) \frac{d y}{d x}=\frac{2 \cos ^{2}(x)-\sin ^{2}(x)+y^{2}}{2 \cos (x)} d x d y = 2 cos ( x ) 2 cos 2 ( x ) − sin 2 ( x ) + y 2
با جایگذاری، میبینیم که این جواب صحیح است و یک معادله ریکاتی داریم. تغییر متغیر زیر را در نظر میگیریم:
z = 1 y − sin ( x ) z=\frac{1}{y-\sin (x)} z = y − sin ( x ) 1
که در نتیجه آن، داریم:
y = sin ( x ) + 1 z y=\sin (x)+\frac{1}{z} y = sin ( x ) + z 1
و مشتق زیر حاصل خواهد شد:
y ′ = cos ( x ) − z ′ z 2 y ^ {\prime}=\cos (x)-\frac{z^{\prime}}{z^{2}} y ′ = cos ( x ) − z 2 z ′
با جایگذاری در معادله، خواهیم داشت:
cos ( x ) − z ′ z 2 = 2 cos 2 ( x ) − sin 2 ( x ) + ( sin ( x ) + 1 z ) 2 2 cos ( x ) \cos (x)-\frac{z^{\prime}}{z^{2}}=\frac{2 \cos ^{2}(x)-\sin ^{2}(x)+\left(\sin (x)+\frac{1}{z}\right)^{2}}{2 \cos (x)} cos ( x ) − z 2 z ′ = 2 cos ( x ) 2 cos 2 ( x ) − sin 2 ( x ) + ( sin ( x ) + z 1 ) 2
با کمی عملیات جبری، به رابطه زیر میرسیم:
− z ′ z 2 = ( 2 sin ( x ) 1 z + 1 z 2 ) 2 cos ( x ) = sin ( x ) cos ( x ) 1 z + 1 2 cos ( x ) 1 z 2 - \frac{ z ^ { \prime } } { z ^ { 2 } } = \frac { \left ( 2 \sin ( x ) \frac { 1 } { z } + \frac { 1 } { z ^ { 2 } } \right ) } { 2 \cos ( x ) } = \frac { \sin ( x ) } { \cos ( x ) } \frac { 1 } { z } + \frac { 1 } { 2 \cos ( x ) } \frac { 1 } { z ^ { 2 } } − z 2 z ′ = 2 cos ( x ) ( 2 sin ( x ) z 1 + z 2 1 ) = cos ( x ) sin ( x ) z 1 + 2 cos ( x ) 1 z 2 1
در نتیجه، میتوانیم بنویسیم:
z ′ = − sin ( x ) cos ( x ) z − 1 2 cos ( x ) z ^ { \prime } = - \frac { \sin ( x ) } { \cos (x)} z-\frac{1}{2 \cos ( x ) } z ′ = − cos ( x ) sin ( x ) z − 2 cos ( x ) 1
اکنون یک معادله خطی داریم که برای حل آن از عامل انتگرالساز کمک میگیریم:
u ( x ) = e ∫ sin ( x ) cos ( x ) = e − ln ( cos ( x ) ) = 1 cos ( x ) = sec ( x ) u ( x ) = e ^ { \int \frac { \sin ( x ) } { \cos ( x ) } } = e ^ { - \ln ( \cos ( x ) ) } = \frac { 1 } { \cos ( x ) } = \sec ( x ) u ( x ) = e ∫ c o s ( x ) s i n ( x ) = e − l n ( c o s ( x )) = cos ( x ) 1 = sec ( x )
جواب عمومی بهصورت زیر است:
z = − 1 / 2 ∫ sec 2 ( x ) d x + C u ( x ) = cos ( x ) ( − 1 2 tan ( x ) + C ) = − 1 2 sin ( x ) + C cos ( x ) \begin {align} z & = \frac { - 1 / 2 \int \sec ^ { 2 } (x ) d x + C } { u ( x ) } \\& = \cos ( x ) \left ( - \frac { 1 } { 2 } \tan ( x ) + C \right ) \\ &= - \frac { 1 } { 2 } \sin ( x ) + C \cos ( x ) \end {align} z = u ( x ) − 1/2 ∫ sec 2 ( x ) d x + C = cos ( x ) ( − 2 1 tan ( x ) + C ) = − 2 1 sin ( x ) + C cos ( x )
اکنون جواب را برای y y y
y = sin ( x ) + 1 − 1 2 sin ( x ) + C cos ( x ) y = \sin ( x ) + \frac { 1 } { - \frac { 1 } { 2 } \sin ( x ) + C \cos ( x ) } y = sin ( x ) + − 2 1 sin ( x ) + C cos ( x ) 1
با در نظر گرفتن شرایط اولیه y ( 0 ) = − 1 y ( 0 ) = - 1 y ( 0 ) = − 1 C = − 1 C = - 1 C = − 1
y = sin ( x ) + 1 − 1 2 sin ( x ) − cos ( x ) y = \sin ( x ) + \frac { 1 } { - \frac { 1 } { 2 } \sin ( x ) - \cos ( x ) } y = sin ( x ) + − 2 1 sin ( x ) − cos ( x ) 1
نمونه سوال معادلات دیفرانسیل ۱۶
جوابهای عمومی و تکین معادله دیفرانسیل y = x y ’ + ( y ’ ) 2 y = x y ’ + { \left ( { y ’ } \right ) ^ 2 } y = x y ’ + ( y ’ ) 2
حل سوال ۱۶: این معادله یک معادله کلرو است. با قرار دادن y ’ = p y’ = p y ’ = p
y = x p + p 2 y = x p + { p ^ 2 } y = x p + p 2
با دیفرانسیلگیری، داریم:
d y = x d p + p d x + 2 p d p { d y = x d p + p d x } + { 2 p d p } d y = x d p + p d x + 2 p d p
اکنون مقدار p d x pdx p d x d y dy d y
$$ \require {cancel}<br />
{ { \cancel { p d x } = x d p + \cancel { p d x } } + { 2 p d p , \; \; } } \Rightarrow<br />
{ d p \left( { x + 2 p } \right ) = 0 } $$
با صفر قرار دادن عامل اول، داریم:
d p = 0 , ⇒ p = C d p = 0 , \; \; \Rightarrow p = C d p = 0 , ⇒ p = C
اکنون معادله بالا را در معادله دیفرانسیل قرار میدهیم:
y = C x + C 2 y = C x + { C ^ 2 } y = C x + C 2
بنابراین، جواب عمومی معادله کلرو، دستهای تکپارامتری از خطوط راست است.
حال عامل دوم را برابر با صفر قرار میدهیم:
x + 2 p = 0 , ⇒ x = – 2 p { x + 2 p = 0 , \; \; } \Rightarrow { x = – 2 p } x + 2 p = 0 , ⇒ x = –2 p
بنابراین، شکل پارامتری جواب تکین معادله دیفرانسیل بهصورت زیر خواهد بود:
{ x = – 2 p y = x p + p 2 \left\{ \begin {array} {l} x = – 2 p \\ y = x p + { p ^ 2 } \end {array} \right . { x = –2 p y = x p + p 2
با حذف p p p
p = – x 2 , ⇒ y = x ( – x 2 ) + ( – x 2 ) 2 = – x 2 2 + x 2 4 = – x 2 4 { p = – \frac { x } { 2 } , \; \; } \Rightarrow { y = x \left ( { – \frac { x } { 2 } } \right ) + { \left ( { – \frac { x } { 2 } } \right ) ^ 2 } } = { – \frac { { { x ^ 2 } } } { 2 } + \frac { { { x ^ 2 } } } { 4 } } = { – \frac { { { x ^ 2 } } } { 4 } } p = – 2 x , ⇒ y = x ( – 2 x ) + ( – 2 x ) 2 = – 2 x 2 + 4 x 2 = – 4 x 2
نمونه سوال معادلات دیفرانسیل ۱۷
جوابهای عمومی و تکین معادله دیفرانسیل y = 2 x y ’– 3 ( y ’ ) 2 y = 2 x y ’ – 3 { \left ( { y ’ } \right ) ^ 2 } y = 2 x y ’–3 ( y ’ ) 2
حل سوال ۱۷: یک معادله لاگرانژ داریم و باید آن را با کمک دیفرانسیلگیری حل کنیم. بدین منظور، تساوی y ’ = p y’ = p y ’ = p
y = 2 x p – 3 p 2 y = 2 x p – 3 { p ^ 2 } y = 2 x p –3 p 2
با دیفرانسیلگیری از دو سمت معادله بالا، داریم:
d y = 2 x d p + 2 p d x − 6 p d p . { d y = 2 x d p + 2 p d x } - { 6 p d p . } d y = 2 x d p + 2 p d x − 6 p d p .
میتوانیم d y dy d y p d x pdx p d x
p d x = 2 x d p + 2 p d x – 6 p d p , ⇒ – p d x = 2 x d p – 6 p d p . { { p d x = 2 x d p } + { 2 p d x – 6 p d p , \; \; } } \Rightarrow { – p d x = 2 x d p – 6 p d p . } p d x = 2 x d p + 2 p d x –6 p d p , ⇒ – p d x = 2 x d p –6 p d p .
با تقسیم تساوی بالا بر p p p p = 0 p=0 p = 0
− d x = 2 x p d p – 6 d p , ⇒ d x d p + 2 p x – 6 = 0. { - d x = \frac { { 2 x } } { p } d p – 6 d p , \; \; } \Rightarrow { \frac { { d x } } { { d p } } + \frac { 2 } { p } x – 6 = 0 . } − d x = p 2 x d p –6 d p , ⇒ d p d x + p 2 x –6 = 0.
همانطور که میبینیم، یک معادله خطی برای x ( p ) x(p) x ( p )
u ( p ) = exp ( ∫ 2 p d p ) = exp ( 2 ln ∣ p ∣ ) = exp ( ln ∣ p ∣ 2 ) = ∣ p ∣ 2 = p 2 . { u \left ( p \right ) = \exp \left ( { \int { \frac { 2 }{ p } d p } } \right ) } = { \exp \left ( { 2 \ln \left | p \right | } \right ) } = { \exp \left ( { \ln { { \left | p \right | } ^ 2 } } \right ) } = { { \left | p \right | ^ 2 } } = { { p ^ 2 } . } u ( p ) = exp ( ∫ p 2 d p ) = exp ( 2 ln ∣ p ∣ ) = exp ( ln ∣ p ∣ 2 ) = ∣ p ∣ 2 = p 2 .
جواب عمومی معادله خطی برابر است با:
x ( p ) = ∫ p 2 ⋅ 6 d p + C p 2 = 6 p 3 3 + C p 2 = 2 p + C p 2 . { x \left ( p \right ) } = { \frac { { \int { { p ^ 2 } \cdot 6 d p } + C } } { { { p ^ 2 } } } } = { \frac { { \frac { { 6 { p ^ 3 } } } { 3 } + C } } { { { p ^ 2 } } } } = { 2 p + \frac { C } { { { p ^ 2 } } } . } x ( p ) = p 2 ∫ p 2 ⋅ 6 d p + C = p 2 3 6 p 3 + C = 2 p + p 2 C .
با قرار دادن عبارت بالا به جای x x x
y = 2 ( 2 p + C p 2 ) p – 3 p 2 = 4 p 2 + 2 C p – 3 p 2 = p 2 + 2 C p . { y } = { 2 \left ( { 2 p + \frac { C } { { { p ^ 2 } } } } \right ) p – 3 { p ^ 2 } } \\ = { 4 { p ^ 2 } + \frac { { 2 C } } { p } – 3 { p ^ 2 } } = { { p ^ 2 } + \frac { { 2 C } } { p } . } y = 2 ( 2 p + p 2 C ) p –3 p 2 = 4 p 2 + p 2 C –3 p 2 = p 2 + p 2 C .
بنابراین، جواب عمومی پارامتری، با دستگاه معادلات زیر تعریف میشود:
{ x ( p ) = 2 p + C p 2 y ( p ) = p 2 + 2 C p . \left \{ \begin {array} {l} x \left ( p \right ) = 2 p + \frac { C } { { { p ^ 2 } } } \\ y \left ( p \right ) = { p ^ 2 } + \frac { { 2 C } } { p } \end {array} \right . . { x ( p ) = 2 p + p 2 C y ( p ) = p 2 + p 2 C .
معادله لاگرانژ ممکن است یک جواب تکین نیز داشته باشد. با حل معادله φ ( p ) – p = 0 \varphi \left ( p \right ) – p = 0 φ ( p ) – p = 0
2 p – p = 0 , ⇒ p = 0 { 2 p – p = 0 , \; \; } \Rightarrow { p = 0 } 2 p – p = 0 , ⇒ p = 0
در نتیجه، جواب تکین با تابع خطی زیر بیان میشود:
y = φ ( 0 ) x + ψ ( 0 ) = 0 ⋅ x + 0 = 0 { y = \varphi \left ( 0 \right ) x + \psi \left ( 0 \right ) } = { 0 \cdot x + 0 } = { 0 } y = φ ( 0 ) x + ψ ( 0 ) = 0 ⋅ x + 0 = 0
نمونه سوال معادلات دیفرانسیل ۱۸
معادله زیر را حل کنید.
y ′ = x + y y ( 0 ) = 1 \begin {aligned}y ^ { \prime } & = x +y \\ y ( 0 ) & = 1 \end {aligned} y ′ y ( 0 ) = x + y = 1
حل سوال ۱۸: در این سوال، از سریها استفاده میکنیم. بدین صورت که عبارت کلی سری را در معادله جایگذاری میکنیم:
∑ n = 1 ∞ n c n x n − 1 = x + ∑ n = 0 x c n x n \sum _ { n = 1 } ^ { \infty } n c _{ n } x ^ { n - 1} = x + \sum _ { n = 0 } ^ { x } c _ { n } x ^ { n } n = 1 ∑ ∞ n c n x n − 1 = x + n = 0 ∑ x c n x n
اکنون ضرایب را در سمت چپ مرتب میکنیم:
∑ n = 1 ∞ n c n x n − 1 − x − ∑ n = 1 ∞ c n x n = 0 \sum _ { n = 1 } ^ { \infty } n c _ { n } x ^ { n - 1 } - x -\sum _ { n = 1 } ^ { \infty } c _ { n } x ^ { n } = 0 n = 1 ∑ ∞ n c n x n − 1 − x − n = 1 ∑ ∞ c n x n = 0
همانطور که مشخص است، چند جمله اول سری بهصورت زیر هستند:
( c 1 + 2 c 2 x + 3 c 3 x 2 + 4 c 4 x 3 + ⋯ ) − x − ( c 0 + c 1 x + c 2 x 2 + c 3 x 3 + ⋯ ) = 0 \begin {aligned} \left ( c _ { 1 } +2 c _ { 2 } x + 3 c _ { 3 } x ^ { 2 } + 4 c _ { 4 } x ^ { 3 } \right. & + \cdots ) \\ & - x - \left ( c _ { 0 } + c _ { 1 } x + c _ { 2 } x ^ { 2 } + c _ { 3 } x ^ { 3 } + \cdots \right ) = 0 \end {aligned} ( c 1 + 2 c 2 x + 3 c 3 x 2 + 4 c 4 x 3 + ⋯ ) − x − ( c 0 + c 1 x + c 2 x 2 + c 3 x 3 + ⋯ ) = 0
جملات را بر اساس درجه متغیرشان مرتب میکنیم و بهصورت زیر مینویسیم:
( c 1 − c 0 ) + ( 2 c 2 − 1 − c 1 ) x + ( 3 c 3 − c 2 ) x 2 + ( 4 c 4 − c 3 ) x 3 + ⋯ = 0 \left ( c _{ 1 } - c _{ 0 } \right ) + \left ( 2 c _ { 2 } - 1 -c _ { 1 } \right ) x + \left ( 3 c _ { 3 } - c _ { 2 } \right ) x ^ { 2 } + \left ( 4 c _ { 4 } - c _ { 3 } \right ) x ^ { 3 } + \cdots = 0 ( c 1 − c 0 ) + ( 2 c 2 − 1 − c 1 ) x + ( 3 c 3 − c 2 ) x 2 + ( 4 c 4 − c 3 ) x 3 + ⋯ = 0
اگر دو جمله اول را در نظر نگیریم، سایر جملات از الگوی زیر پیروی میکنند:
( c 1 − c 0 ) + ( 2 c 2 − 1 − c 1 ) x + ∑ n = 3 x ( n c n − c n − 1 ) x n − 1 = 0 \left ( c _ { 1 } - c _ { 0 } \right ) + \left ( 2 c _ { 2 } - 1 -c _ { 1 } \right ) x + \sum _ { n = 3 } ^ { x } \left ( n c _ { n } -c _ { n - 1 } \right ) x ^ { n - 1 } = 0 ( c 1 − c 0 ) + ( 2 c 2 − 1 − c 1 ) x + n = 3 ∑ x ( n c n − c n − 1 ) x n − 1 = 0
برای آنکه این معادله بهازای هر x x x
c 1 − c 0 = 0 , 2 c 2 − 1 − c 1 = 0 , n c n − c n − 1 = 0 , n ≥ 3 c _ {1 } - c _ { 0 } = 0 , \quad 2 c _ { 2 }- 1 - c _ { 1 } = 0 , \;\;\;\; n c_{n}-c_{n-1}=0 , \;\;\;\;n \geq 3 c 1 − c 0 = 0 , 2 c 2 − 1 − c 1 = 0 , n c n − c n − 1 = 0 , n ≥ 3
جمله آخر، یک تصاعد حسابی است که میتوان آن را بهشکل زیر بیان کرد:
c n = c n − 1 n , n ≥ 3 c _ { n } = \frac { c _ { n - 1 } } { n } \text {, }\;\;\; n \geq 3 c n = n c n − 1 , n ≥ 3
از معادله (*) این نتیجه گرفته میشود که c 1 c _ 1 c 1 c 0 c _ 0 c 0 c 2 = 1 2 ( 1 + c 1 ) c _ 2 = \frac 12 (1+c_1) c 2 = 2 1 ( 1 + c 1 ) تصاعد حسابی بهصورت زیر بهدست میآید:
c 3 = c 2 3 = 1 2 ( 1 + c 0 ) 3 = 1 + c 0 2 ⋅ 3 c 4 = c 3 4 = 1 + c 0 2 ⋅ 3 ⋅ 4 \begin{aligned} & c _ { 3 } = \frac { c _ { 2 } } { 3 } = \frac { \frac { 1 }{ 2 } \left ( 1 + c _ { 0 } \right ) } { 3} = \frac { 1 + c _{ 0 } } { 2 \cdot 3 } \\ & c _ { 4 } = \frac {c _ { 3} }{ 4} = \frac { 1 + c _ { 0 } } { 2 \cdot 3 \cdot 4 } \end {aligned} c 3 = 3 c 2 = 3 2 1 ( 1 + c 0 ) = 2 ⋅ 3 1 + c 0 c 4 = 4 c 3 = 2 ⋅ 3 ⋅ 4 1 + c 0
رابطه بالا به همین شکل، برای بقیه ضرایب نیز ادامه دارد. با جمع کردن تمامی این عبارات، سری توانی مد نظر بهصورت زیر قابل بیان است.
y = c 0 + c 1 x + c 2 x 2 + c 3 x 3 + c 4 x 4 + ⋯ = c 0 + c 0 x + 1 + c 0 2 x 2 + 1 + c 0 2 ⋅ 3 x 3 + 1 + c 0 2 ⋅ 3 ⋅ 4 x 4 + ⋯ = c 0 + c 0 x + ( 1 + c 0 ) ( 1 2 x 2 + 1 2 ⋅ 3 x 3 + 1 2 ⋅ 3 ⋅ 4 x 4 + ⋯ ) = c 0 + c 0 x + ( 1 + c 0 ) ∑ n = 2 ∞ 1 n ! x n \begin {aligned} y & = c _ { 0 } + c _ { 1 } x + c _ { 2 } x ^ { 2 } +c _ { 3} x ^ { 3 } + c _{ 4 } x ^ { 4 } + \cdots \\ & = c _ { 0 } + c _ { 0 } x + \frac { 1 + c _ { 0 } } { 2 } x ^ { 2 } + \frac { 1 +c _ { 0 } } { 2 \cdot 3 } x ^ { 3 } + \frac { 1 + c _ { 0 } } { 2 \cdot 3 \cdot 4 } x ^ { 4 } + \cdots \\ & = c _ { 0 } + c _ { 0 } x + \left ( 1 + c _ { 0 } \right ) \left ( \frac { 1 } { 2 } x ^ { 2 } + \frac { 1 } { 2 \cdot 3 } x ^ { 3 } + \frac { 1 } { 2 \cdot 3 \cdot 4 } x ^ { 4 } + \cdots \right ) \\ & = c _ { 0 } + c _ { 0 } x + \left(1+c_{0}\right) \sum_{n=2}^{\infty} \frac{1}{n !} x^{n} \end{aligned} y = c 0 + c 1 x + c 2 x 2 + c 3 x 3 + c 4 x 4 + ⋯ = c 0 + c 0 x + 2 1 + c 0 x 2 + 2 ⋅ 3 1 + c 0 x 3 + 2 ⋅ 3 ⋅ 4 1 + c 0 x 4 + ⋯ = c 0 + c 0 x + ( 1 + c 0 ) ( 2 1 x 2 + 2 ⋅ 3 1 x 3 + 2 ⋅ 3 ⋅ 4 1 x 4 + ⋯ ) = c 0 + c 0 x + ( 1 + c 0 ) n = 2 ∑ ∞ n ! 1 x n
توجه داشته باشید که برای محاسبه c 0 c_0 c 0
y ( 0 ) = 1 ⇒ [ c 0 + c 0 x + ( 1 + c 0 ) ∑ n = 2 ∞ 1 n ! x n ] x = 0 = 1 ⇒ c 0 = 1 y ( 0) = 1 \Rightarrow\left[ c _{ 0 } + c _ { 0 } x + \left ( 1+ c _ { 0 } \right ) \sum _ {n = 2 } ^ {\infty} \frac{1}{n !} x^{n}\right]_{x=0}=1 \Rightarrow c_{0}=1 y ( 0 ) = 1 ⇒ [ c 0 + c 0 x + ( 1 + c 0 ) n = 2 ∑ ∞ n ! 1 x n ] x = 0 = 1 ⇒ c 0 = 1
نهایتاً پاسخ معادله مقدار اولیه مفروض، بهصورت زیر بدست میآید:
y = 1 + x + ∑ n = 2 ∞ 2 n ! x n ( ∗ ∗ ) y=1+x + \sum _ {n = 2 } ^ { \infty } \frac { 2} { n ! } x ^ { n } \quad(* *) y = 1 + x + n = 2 ∑ ∞ n ! 2 x n ( ∗ ∗ )
با توجه به بسط تیلور e x e ^x e x ∑ n = 2 ∞ 1 n ! x n = e x − x − 1 \sum _{n=2}^{\infty} \frac {1 } { n !} x ^ n =e ^ x - x -1 n = 2 ∑ ∞ n ! 1 x n = e x − x − 1
y = 1 + x + 2 ( e x − x − 1 ) = − 1 − x + 2 e x y = 1 + x + 2(e ^ x - x - 1 ) = -1-x +2e ^ x y = 1 + x + 2 ( e x − x − 1 ) = − 1 − x + 2 e x
نمونه سوال معادلات دیفرانسیل ۱۹
جوابهای تکین معادله دیفرانسیل ( y ’ ) 2 ( 1 – y ) 2 = 2 – y {\left( {y’} \right)^2}{\left( {1 – y} \right)^2}= 2 – y ( y ’ ) 2 ( 1– y ) 2 = 2– y
حل سوال ۱۹: ابتدا مبین p p p x x x
2 y ’ ( 1 – y ) 2 = 0. 2 y ’ { \left( { 1 – y } \right) ^ 2 } = 0 . 2 y ’ ( 1– y ) 2 = 0.
عبارت y ’ y’ y ’
{ ( y ’ ) 2 ( 1 – y ) 2 = 2 – y y ’ ( 1 – y ) 2 = 0 . \left\{ \begin {array} {l} { \left( { y ’ } \right) ^ 2 } { \left( { 1 – y } \right) ^ 2 } = 2 – y \\ y ’ { \left( { 1 – y } \right) ^ 2 } = 0 \end {array} \right . . { ( y ’ ) 2 ( 1– y ) 2 = 2– y y ’ ( 1– y ) 2 = 0 .
بنابراین، داریم:
( y ’ ) 2 = 2 – y ( 1 – y ) 2 , ⇒ 2 – y ( 1 – y ) 2 ⋅ ( 1 – y ) 4 = 0 , ⇒ ( 1 – y ) 2 ( 2 – y ) = 0. {{\left( {y’} \right)^2} = \frac{{2 – y}}{{{{\left( {1 – y} \right)}^2}}},\;\;}\Rightarrow {\frac{{2 – y}}{{{{\left( {1 – y} \right)}^2}}} \cdot {\left( {1 – y} \right)^4} = 0,\;\;}\Rightarrow {{\left( {1 – y} \right)^2}\left( {2 – y} \right) = 0.} ( y ’ ) 2 = ( 1– y ) 2 2– y , ⇒ ( 1– y ) 2 2– y ⋅ ( 1– y ) 4 = 0 , ⇒ ( 1– y ) 2 ( 2– y ) = 0.
اکنون مبین C C C
( d y d x ) 2 = 2 – y ( 1 – y ) 2 , ⇒ d y d x = ± 2 – y 1 – y , ⇒ ( 1 – y ) d y 2 – y = ± d x . {{\left( {\frac{{dy}}{{dx}}} \right)^2} = \frac{{2 – y}}{{{{\left( {1 – y} \right)}^2}}},\;\;}\Rightarrow {\frac{{dy}}{{dx}} = \pm \frac{{\sqrt {2 – y} }}{{1 – y}},\;\;}\\ \Rightarrow {\frac{{\left( {1 – y} \right)dy}}{{\sqrt {2 – y} }} = \pm dx.} ( d x d y ) 2 = ( 1– y ) 2 2– y , ⇒ d x d y = ± 1– y 2– y , ⇒ 2– y ( 1– y ) d y = ± d x .
با انتگرالگیری از طرفین، داریم:
∫ ( 1 – y ) d y 2 – y = ± ∫ d x + C . {\int {\frac{{\left( {1 – y} \right)dy}}{{\sqrt {2 – y} }}} }={ \pm \int {dx} + C.} ∫ 2– y ( 1– y ) d y = ± ∫ d x + C .
برای حل انتگرال سمت چپ از تغییر متغیر استفاده میکنیم:
2 – y = t , ⇒ d y = – d t , ⇒ 1 – y = t – 1. {2 – y = t,\;\; }\Rightarrow {dy = – dt,\;\;}\Rightarrow {1 – y = t – 1.} 2– y = t , ⇒ d y = – d t , ⇒ 1– y = t –1.
خواهیم داشت:
∫ ( t – 1 ) ( – d t ) t = ± x + C , ⇒ ∫ ( t – 1 t ) d t = ∓ x – C , ⇒ t 3 2 3 2 – t 1 2 1 2 = ∓ x – C , ⇒ 2 3 t 3 2 – 2 t 1 2 = ∓ x – C , ⇒ 2 3 ( 2 – y ) 3 2 − 2 ( 2 – y ) 1 2 = ∓ x – C , ⇒ 2 3 2 – y ( 2 – y – 3 ) = ∓ x – C , ⇒ 4 9 ( 2 – y ) ( y + 1 ) 2 = ( x + C ) 2 , ⇒ 4 ( 2 – y ) ( y + 1 ) 2 = 9 ( x + C ) 2 . {{\int {\frac{{\left( {t – 1} \right)\left( { – dt} \right)}}{{\sqrt t }}} }={ \pm x + C,\;\;}}\Rightarrow {{\int {\left( {\sqrt t – \frac{1}{{\sqrt t }}} \right)dt} }={ \mp x – C,\;\;}}\\ \Rightarrow {{\frac{{{t^{ \frac{3}{2}\normalsize}}}}{{\frac{3}{2}}} – \frac{{{t^{ \frac{1}{2}\normalsize}}}}{{\frac{1}{2}}} }={ \mp x – C,\;\;}}\Rightarrow {{\frac{2}{3}{t^{ \frac{3}{2}\normalsize}} – 2{t^{ \frac{1}{2}\normalsize}} }={ \mp x – C,\;\;}} \\ \Rightarrow {{\frac{2}{3}{\left( {2 – y} \right)^{ \frac{3}{2}\normalsize}} }-{ 2{\left( {2 – y} \right)^{ \frac{1}{2}\normalsize}} }={ \mp x – C,\;\;}}\Rightarrow {{\frac{2}{3}\sqrt {2 – y} \left( {2 – y – 3} \right) }={ \mp x – C,\;\;}} \\ \Rightarrow {{\frac{4}{9}\left( {2 – y} \right){\left( {y + 1} \right)^2} }={ {\left( {x + C} \right)^2},\;\;}}\Rightarrow {{4\left( {2 – y} \right){\left( {y + 1} \right)^2} }={ 9{\left( {x + C} \right)^2}.}} ∫ t ( t –1 ) ( – d t ) = ± x + C , ⇒ ∫ ( t – t 1 ) d t = ∓ x – C , ⇒ 2 3 t 2 3 – 2 1 t 2 1 = ∓ x – C , ⇒ 3 2 t 2 3 –2 t 2 1 = ∓ x – C , ⇒ 3 2 ( 2– y ) 2 3 − 2 ( 2– y ) 2 1 = ∓ x – C , ⇒ 3 2 2– y ( 2– y –3 ) = ∓ x – C , ⇒ 9 4 ( 2– y ) ( y + 1 ) 2 = ( x + C ) 2 , ⇒ 4 ( 2– y ) ( y + 1 ) 2 = 9 ( x + C ) 2 .
از جواب عمومی نسبت به C C C
0 = 18 ( x + C ) . 0 = 18\left( {x + C} \right). 0 = 18 ( x + C ) .
با قرار دادن x + C = 0 x + C = 0 x + C = 0 C C C
( y + 1 ) 2 ( 2 – y ) = 0. {\left( {y + 1} \right)^2}\left( {2 – y} \right) = 0. ( y + 1 ) 2 ( 2– y ) = 0.
اکنون میتوانیم معادلات مبین p p p C C C
ψ p ( y ) = ( 1 – y ) 2 ( 2 – y ) = 0 , ψ C ( y ) = ( y + 1 ) 2 ( 2 – y ) = 0. {{\psi _p}\left( y \right) }={ {\left( {1 – y} \right)^2}\left( {2 – y} \right) }={ 0,} \\ {{\psi _C}\left( y \right) }={ {\left( {y + 1} \right)^2}\left( {2 – y} \right) }={ 0.} ψ p ( y ) = ( 1– y ) 2 ( 2– y ) = 0 , ψ C ( y ) = ( y + 1 ) 2 ( 2– y ) = 0.
از ساختار این معادلات نتیجه گرفته میشود که معادله 2 − y = 0 2-y=0 2 − y = 0 p p p
( 1 – y ) 2 = 0 , ⇒ y = 1. {{\left( {1 – y} \right)^2} = 0,\;\; }\Rightarrow {y = 1.} ( 1– y ) 2 = 0 , ⇒ y = 1.
و به طور مشابه، از معادله مبین C C C
( y + 1 ) 2 = 0 , ⇒ y = – 1. {{\left( {y + 1} \right)^2} = 0,\;\; }\Rightarrow {y = – 1.} ( y + 1 ) 2 = 0 , ⇒ y = –1.
در این مثال، فقط پوش y = 2 y=2 y = 2
نمونه سوال معادلات دیفرانسیل ۲۰
معادله دیفرانسیل زیر را حل کنید.
3 y ′ ′ + 2 y ′ − 8 y = 0 y ( 0 ) = − 6 y ′ ( 0 ) = − 18 3y'' + 2y' - 8y = 0\hspace{0.25in}y\left( 0 \right) = - 6\hspace{0.25in}y'\left( 0 \right) = - 18 3 y ′′ + 2 y ′ − 8 y = 0 y ( 0 ) = − 6 y ′ ( 0 ) = − 18
حل سوال ۲۰: معادله مشخصه بهصورت زیر است:
3 r 2 + 2 r − 8 = 0 ( 3 r − 4 ) ( r + 2 ) = 0 \begin{align*}3{r^2} + 2r - 8 & = 0\\ \left( {3r - 4} \right)\left( {r + 2} \right) & = 0\end{align*} 3 r 2 + 2 r − 8 ( 3 r − 4 ) ( r + 2 ) = 0 = 0
ریشههای این معادله r 1 = 4 3 r_{1} = \frac{4}{3} r 1 = 3 4 r 2 = − 2 r_{2} = -2 r 2 = − 2
y ( t ) = c 1 e 4 t 3 + c 2 e − 2 t y ′ ( t ) = 4 3 c 1 e 4 t 3 − 2 c 2 e − 2 t \begin{align*} y \left( t \right) & = {c_1}{{\bf{e}}^{\frac{{ 4 \,t}}{3}}} + {c_2}{{\bf{e}}^{ - 2t}}\\ y'\left( t \right) & = \frac{4}{3}{c_1}{{\bf{e}}^{\frac{{4t}}{3}}} - 2{c_2}{{\bf{e}}^{ - 2t}}\end{align*} y ( t ) y ′ ( t ) = c 1 e 3 4 t + c 2 e − 2 t = 3 4 c 1 e 3 4 t − 2 c 2 e − 2 t
اکنون شرایط اولیه را در معادلههای اخیر قرار میدهیم تا ثابتها را محاسبه کنیم:
− 6 = y ( 0 ) = c 1 + c 2 − 18 = y ′ ( 0 ) = 4 3 c 1 − 2 c 2 \begin{align*} - 6 = y \left ( 0 \right ) & = { c _ 1 } + { c _ 2 } \\ - 1 8 = y' \left ( 0 \right ) & = \frac { 4 } { 3 } { c _ 1 } - 2 { c _ 2 } \end {align*} − 6 = y ( 0 ) − 18 = y ′ ( 0 ) = c 1 + c 2 = 3 4 c 1 − 2 c 2
با حل این دستگاه معادلات به جوابهای c 1 = − 9 c_{1} = -9 c 1 = − 9 c 2 = 3 c_{2} = 3 c 2 = 3
y ( t ) = − 9 e 4 t 3 + 3 e − 2 t y\left( t \right) = - 9{{\bf{e}}^{\frac{{4t}}{3}}} + 3{{\bf{e}}^{ - 2t}} y ( t ) = − 9 e 3 4 t + 3 e − 2 t
نمونه سوال معادلات دیفرانسیل ۲۱
معادله دیفرانسیل زیر را حل کنید.
4 y ′ ′ + 24 y ′ + 37 y = 0 y ( π ) = 1 y ′ ( π ) = 0 4y'' + 24y' + 37y = 0\hspace{0.25in}y\left( \pi \right) = 1\hspace{0.25in}y'\left( \pi \right) = 0 4 y ′′ + 24 y ′ + 37 y = 0 y ( π ) = 1 y ′ ( π ) = 0
حل سوال ۲۱: معادله مشخصه بهصورت زیر است:
4 r 2 + 24 r + 37 = 0 4{r^2} + 24r + 37 = 0 4 r 2 + 24 r + 37 = 0
ریشههای این معادله r 1 , 2 = − 3 ± 1 2 i {r_{1,2}} = - 3 \pm \frac{1}{2}\,i r 1 , 2 = − 3 ± 2 1 i
y ( t ) = c 1 e − 3 t cos ( t 2 ) + c 2 e − 3 t sin ( t 2 ) y ′ ( t ) = − 3 c 1 e − 3 t cos ( t 2 ) − c 1 2 e − 3 t sin ( t 2 ) − 3 c 2 e − 3 t sin ( t 2 ) + c 2 2 e − 3 t cos ( t 2 ) \begin {align*}y\left( t \right) & = {c_1}{{\bf{e}}^{ - 3t}}\cos \left( { \frac { t } { 2 } } \right ) + { c _ 2 } { { \bf { e } } ^ { - 3 t } } \sin \left ( { \frac { t } {2 } } \right)\\ y'\left ( t \right) & = - 3 { c _ 1 } { { \bf { e } } ^ { - 3 t } } \cos \left( { \frac { t } { 2 } } \right) - \frac{{{c_1}}}{2}{{\bf{e } } ^ { - 3 t } } \sin \left ( { \frac {t } { 2 } } \right ) - 3 { c _ 2 } { { \bf { e } } ^ { - 3 t } } \sin \left( {\frac{t}{2}} \right) + \frac{{{c_2}}}{2}{{\bf{e}}^{ - 3t}}\cos \left( {\frac{t}{2}} \right)\end{align*} y ( t ) y ′ ( t ) = c 1 e − 3 t cos ( 2 t ) + c 2 e − 3 t sin ( 2 t ) = − 3 c 1 e − 3 t cos ( 2 t ) − 2 c 1 e − 3 t sin ( 2 t ) − 3 c 2 e − 3 t sin ( 2 t ) + 2 c 2 e − 3 t cos ( 2 t )
با قرار دادن شرایط اولیه، مقدار ثابتهای c 1 c _ 1 c 1 c 2 c _ 2 c 2
1 = y ( π ) = c 1 e − 3 π cos ( π 2 ) + c 2 e − 3 π sin ( π 2 ) = c 2 e − 3 π 0 = y ′ ( π ) = − c 1 2 e − 3 π − 3 c 2 e − 3 π \begin {align*} 1 & = y \left ( \pi \right ) = { c _ 1 } { { \bf { e } } ^ { - 3 \pi } } \cos \left ( {\frac { \pi } { 2 } } \right ) + { c _ 2 } { { \bf { e } } ^ { - 3 \pi } } \sin \left( {\frac{\pi }{2}} \right) = {c_2}{{\bf{e}}^{ - 3\pi }}\\ 0 & = y'\left( \pi \right) = - \frac{{{c_1}}}{2}{{\bf{e}}^{ - 3\pi }} - 3{c_2}{{\bf{e}}^{ - 3\pi }}\end{align*} 1 0 = y ( π ) = c 1 e − 3 π cos ( 2 π ) + c 2 e − 3 π sin ( 2 π ) = c 2 e − 3 π = y ′ ( π ) = − 2 c 1 e − 3 π − 3 c 2 e − 3 π
که برابر خواهند بود با
c 1 = − 6 e 3 π c 2 = e 3 π {c_1} = - 6{{\bf{e}}^{3\pi }}\hspace{0.25in}{c_2} = {{\bf{e}}^{3\pi }} c 1 = − 6 e 3 π c 2 = e 3 π
در نتیجه، جواب معادله بهصورت زیر است:
y ( t ) = − 6 e 3 π e − 3 t cos ( t 2 ) + e 3 π e − 3 t sin ( t 2 ) y ( t ) = − 6 e − 3 ( t − π ) cos ( t 2 ) + e − 3 ( t − π ) sin ( t 2 ) \begin {align*} y \left ( t \right ) & = - 6 { { \bf { e } } ^ { 3 \pi } } { { \bf { e } } ^ { - 3 t } } \cos \left ( { \frac { t } { 2 } } \right ) + { { \bf { e } } ^ { 3 \pi } } { { \bf { e } } ^ { - 3 t } } \sin \left ( { \frac { t } { 2 } } \right ) \\ y \left ( t \right ) & = - 6 { { \bf { e } } ^ { - 3 \left ( { t - \pi } \right ) } } \cos \left ( { \frac { t } { 2 } } \right ) + { { \bf { e } } ^ { - 3 \left ( { t - \pi } \right ) } } \sin \left ( { \frac { t } { 2 } } \right ) \end {align*} y ( t ) y ( t ) = − 6 e 3 π e − 3 t cos ( 2 t ) + e 3 π e − 3 t sin ( 2 t ) = − 6 e − 3 ( t − π ) cos ( 2 t ) + e − 3 ( t − π ) sin ( 2 t )
نمونه سوال معادلات دیفرانسیل ۲۲
معادله دیفرانسیل زیر را حل کنید.
y ′ ′ + 14 y ′ + 49 y = 0 y ( − 4 ) = − 1 y ′ ( − 4 ) = 5 y'' + 14y' + 49y = 0\hspace{0.25in}y\left( { - 4} \right) = - 1\hspace{0.25in}y'\left( { - 4} \right) = 5 y ′′ + 14 y ′ + 49 y = 0 y ( − 4 ) = − 1 y ′ ( − 4 ) = 5
حل سوال ۲۲: ابتدا معادله مشخصه را تعیین میکنیم:
r 2 + 14 r + 49 = ( r + 7 ) 2 = 0 r 1 , 2 = − 7 {r^2} + 14r + 49 = {\left( {r + 7} \right)^2} = 0\hspace{0.25in}{r_{1,2}} = - 7 r 2 + 14 r + 49 = ( r + 7 ) 2 = 0 r 1 , 2 = − 7
جواب عمومی بهصورت زیر است:
y ( t ) = c 1 e − 7 t + c 2 t e − 7 t y ′ ( t ) = − 7 c 1 e − 7 t + c 2 e − 7 t − 7 c 2 t e − 7 t \begin{align*}y\left( t \right) & = {c_1}{{\bf{e}}^{ - 7t}} + {c_2}t{{\bf{e}}^{ - 7t}}\\ y'\left( t \right) & = - 7{c_1}{{\bf{e}}^{ - 7t}} + {c_2}{{\bf{e}}^{ - 7t}} - 7{c_2}t{{\bf{e}}^{ - 7t}}\end{align*} y ( t ) y ′ ( t ) = c 1 e − 7 t + c 2 t e − 7 t = − 7 c 1 e − 7 t + c 2 e − 7 t − 7 c 2 t e − 7 t
شرایط اولیه را در معادلات بالا قرار میدهیم:
− 1 = y ( − 4 ) = c 1 e 28 − 4 c 2 e 28 5 = y ′ ( − 4 ) = − 7 c 1 e 28 + c 2 e 28 + 28 c 2 e 28 = − 7 c 1 e 28 + 29 c 2 e 28 \begin {align*} - 1 & = y\left( { - 4} \right) = {c_1}{{\bf{e}}^{28}} - 4{c_2}{{\bf{e}}^{28}}\\ 5 & = y'\left( { - 4} \right) = - 7 { c _ 1 } { { \bf { e} } ^ { 2 8 }} + { c _ 2 }{{\bf{e}}^{28}} + 28{c_2}{{\bf{e}}^{28}} = - 7{c_1} { { \bf { e } } ^ { 2 8 } } + 2 9 { c _ 2 } { { \bf { e } } ^ { 2 8 } } \end {align*} − 1 5 = y ( − 4 ) = c 1 e 28 − 4 c 2 e 28 = y ′ ( − 4 ) = − 7 c 1 e 28 + c 2 e 28 + 28 c 2 e 28 = − 7 c 1 e 28 + 29 c 2 e 28
که نتیجه آن اینگونه است:
c 1 = − 9 e − 28 c 2 = − 2 e − 28 {c_1} = - 9{{\bf{e}}^{ - 28}}\hspace{0.25in}{c_2} = - 2{{\bf{e}}^{ - 28}} c 1 = − 9 e − 28 c 2 = − 2 e − 28
در نهایت، جواب معادله بهصورت زیر خواهد بود:
y ( t ) = − 9 e − 28 e − 7 t − 2 t e − 28 e − 7 t y ( t ) = − 9 e − 7 ( t + 4 ) − 2 t e − 7 ( t + 4 ) \begin{align*}y\left( t \right) & = - 9{{\bf{e}}^{ - 28}}{{\bf{e}}^{ - 7t}} - 2t{{\bf{e}}^{ - 28}}{{\bf{e}}^{ - 7t}}\\ y\left( t \right) & = - 9{{\bf{e}}^{ - 7\left( {t + 4} \right)}} - 2t{{\bf{e}}^{ - 7\left( {t + 4} \right)}}\end{align*} y ( t ) y ( t ) = − 9 e − 28 e − 7 t − 2 t e − 28 e − 7 t = − 9 e − 7 ( t + 4 ) − 2 t e − 7 ( t + 4 )
نمونه سوال معادلات دیفرانسیل ۲۳
معادله دیفرانسیل زیر را حل کنید:
x y ′ ′ = ( y ’ ) 2 \sqrt x y^{\prime\prime} = {\left( {y’} \right)^2} x y ′′ = ( y ’ ) 2
حل سوال ۲۳: این معادله صریحاً شامل متغیر y y y y ’ = p ( x ) y’ = p\left( x \right) y ’ = p ( x )
x p ’ = p 2 \sqrt x p’ = {p^2} x p ’ = p 2
این معادله را میتوان با جداسازی متغیرها حل کرد:
x d p d x = p 2 , ⇒ d p p 2 = d x x , ⇒ ∫ d p p 2 = ∫ d x x , ⇒ – 1 p = 2 x + C 1 , ⇒ p = y ’ = – 1 2 x + C 1 . {\sqrt x \frac{{dp}}{{dx}} = {p^2},\;\;}\Rightarrow {\frac{{dp}}{{{p^2}}} = \frac{{dx}}{{\sqrt x }},\;\;}\\ \Rightarrow {\int {\frac{{dp}}{{{p^2}}}} = \int {\frac{{dx}}{{\sqrt x }}} ,\;\;}\Rightarrow { – \frac{1}{p} = 2\sqrt x + {C_1},\;\;}\\ \Rightarrow {p = y’ = \frac{{ – 1}}{{2\sqrt x + {C_1}}}.} x d x d p = p 2 , ⇒ p 2 d p = x d x , ⇒ ∫ p 2 d p = ∫ x d x , ⇒ – p 1 = 2 x + C 1 , ⇒ p = y ’ = 2 x + C 1 –1 .
با انتگرالگیری از معادله اخیر، میتوان تابع y ( x ) y(x) y ( x )
d y d x = – 1 2 x + C 1 , ⇒ d y = – d x 2 x + C 1 , ⇒ y = – ∫ d x 2 x + C 1 . {\frac{{dy}}{{dx}} = \frac{{ – 1}}{{2\sqrt x + {C_1}}},\;\;}\Rightarrow {dy = – \frac{{dx}}{{2\sqrt x + {C_1}}},\;\;}\\ \Rightarrow {y = – \int {\frac{{dx}}{{2\sqrt x + {C_1}}}} .} d x d y = 2 x + C 1 –1 , ⇒ d y = – 2 x + C 1 d x , ⇒ y = – ∫ 2 x + C 1 d x .
برای محاسبه انتگرال، از تغییر متغیر x = t 2 x = {t^2} x = t 2 d x = 2 t d t dx = 2tdt d x = 2 t d t
y = – ∫ d x 2 x + C 1 = – ∫ 2 t d t 2 t + C 1 = – ∫ 2 t + C 1 – C 1 2 t + C 1 d t = – ∫ ( 1 – C 1 2 t + C 1 ) d t = – t + C 1 ∫ d t 2 t + C 1 = – t + C 1 2 ∫ d ( 2 t + C 1 ) 2 t + C 1 = – t + C 1 2 ln ∣ 2 t + C 1 ∣ + C 2 . {y = – \int {\frac{{dx}}{{2\sqrt x + {C_1}}}} } = { – \int {\frac{{2tdt}}{{2t + {C_1}}}} } \\ = { – \int {\frac{{2t + {C_1} – {C_1}}}{{2t + {C_1}}}dt} } = { – \int {\left( {1 – \frac{{{C_1}}}{{2t + {C_1}}}} \right)dt} } \\ = { – t + {C_1}\int {\frac{{dt}}{{2t + {C_1}}}} } = { – t + \frac{{{C_1}}}{2}\int {\frac{{d\left( {2t + {C_1}} \right)}}{{2t + {C_1}}}} } \\ = { – t + \frac{{{C_1}}}{2}\ln \left| {2t + {C_1}} \right| }+{ {C_2}.} y = – ∫ 2 x + C 1 d x = – ∫ 2 t + C 1 2 t d t = – ∫ 2 t + C 1 2 t + C 1 – C 1 d t = – ∫ ( 1– 2 t + C 1 C 1 ) d t = – t + C 1 ∫ 2 t + C 1 d t = – t + 2 C 1 ∫ 2 t + C 1 d ( 2 t + C 1 ) = – t + 2 C 1 ln ∣ 2 t + C 1 ∣ + C 2 .
نوشتن این معادله برای متغیر x x x
y = – x + C 1 2 ln ∣ 2 x + C 1 ∣ + C 2 . {y = – \sqrt x }+{ \frac{{{C_1}}}{2}\ln \left| {2\sqrt x + {C_1}} \right| }+{ {C_2}.} y = – x + 2 C 1 ln 2 x + C 1 + C 2 .
نمونه سوال معادلات دیفرانسیل ۲۴
جواب عمومی دستگاه معادلات خطی زیر را به دست آورید:
d x d t = x – y , d y d t = x + 3 y . { \frac { { d x } } { { d t } } = x – y , \; \; }\kern-0.3pt { \frac { { d y } } { { d t} } = x + 3 y . } d t d x = x – y , d t d y = x + 3 y .
حل سوال ۲۴: ابتدا مقادیر ویژه λ i \lambda _ i λ i A A A
$$ \begin {align*} { { \det \left ( { A – \lambda I } \right ) } = { \left | { \begin {array} { * { 2 0 } { c } }<br />
{ 1 – \lambda } & { – 1 } \\<br />
1 & { 3 – \lambda }<br />
\end {array} } \right | = 0 , \; \; } } \Rightarrow<br />
{ \left ( { 1 – \lambda } \right ) \left ( { 3 – \lambda } \right ) + 1 = 0 , \; \; } \\ \Rightarrow<br />
{ { 3 – 3 \lambda – \lambda } + { { \lambda ^ 2 } + 1 = 0 , \; \; } } \Rightarrow<br />
{ { \lambda ^ 2 } – 4 \lambda + 4 = 0 , \; \; } \Rightarrow<br />
{ { \left ( { \lambda – 2 } \right ) ^ 2 } = 0 . } \end {align*} $$
بنابراین، مقادیر ویژه A A A λ i = 2 \lambda _ i = 2 λ i = 2 k 1 = 2 k _ 1 = 2 k 1 = 2 A – λ 1 I A – {\lambda _1}I A – λ 1 I λ 1 = 2 {\lambda _1} = 2 λ 1 = 2
$$ { \left [ { \begin {array} { * { 2 0 } { c } }<br />
{ 1 – 2 } & { – 1 } \\<br />
1 & { 3 – 2 }<br />
\end {array} } \right ] } \sim { \left [ { \begin {array} { * { 2 0 } { c } }<br />
{ – 1 } & { – 1 } \\<br />
1 & 1<br />
\end {array} } \right ] }<br />
\sim { \left . { \left [ { \begin {array} { * { 2 0 } { c } }<br />
1 & 1 \\<br />
{ – 1 } & { – 1 }<br />
\end {array} } \right ] } \right | \left . { \begin {array} { * { 20 } { c } }<br />
{ } \\<br />
\small { { R _ 2 } + { R _ 1 } } \normalsize<br />
\end {array} } \right . } \\<br />
\sim {\left[ {\begin{array}{*{20}{c}}<br />
1&1\\<br />
0&0<br />
\end{array}} \right] }<br />
\sim {\left( {\begin{array}{*{20}{c}}<br />
1&1<br />
\end{array}} \right).} $$
بنابراین، رتبه ماتریس A – λ 1 I A – {\lambda _1}I A – λ 1 I 1 1 1 s 1 = 1 {s_1} = 1 s 1 = 1 λ 1 = 2 {\lambda _1} = 2 λ 1 = 2
s 1 = n –rank ( A – λ 1 I ) = 2 – 1 = 1. { { s _ 1 } } = { n – \text {rank} \left ( { A – { \lambda _ 1 } I } \right ) } = { 2 – 1 } = { 1 . } s 1 = n – rank ( A – λ 1 I ) = 2–1 = 1.
جواب برداری عمومی به صورت زیر است:
$$ { \mathbf { X } \left ( t \right ) } = { \left [ { \begin {array} { * { 2 0 } { c } }<br />
x \\<br />
y<br />
\end {array} } \right ] + { \mathbf { P } _ { { k _ i } – { s _ i } } } \left ( t \right ) { e ^ { { \lambda _ i } t } } }<br />
= { { \mathbf { P } _ 1 } \left ( t \right ) { e ^ { { \lambda _ i } t } } }<br />
= { \left ( { { \mathbf { A } _ 0 } + { \mathbf { A } _ 1 } t } \right ) { e ^ { 2 t } } . } $$
اکنون از روش ضرایب نامعین استفاده میکنیم. عبارات زیر را در نظر بگیرید:
x = ( a 0 + a 1 t ) e 2 t , y = ( b 0 + b 1 t ) e 2 t . { x = \left ( { { a _ 0 } + { a _ 1 } t } \right ){ e ^ { 2 t } } , \; \; } \kern-0.3pt { y = \left ( { { b _ 0 } + { b _ 1} t } \right ){ e ^ { 2 t } } . } x = ( a 0 + a 1 t ) e 2 t , y = ( b 0 + b 1 t ) e 2 t .
مشتقات برابرند با
d x d t = a 1 e 2 t + 2 ( a 0 + a 1 t ) e 2 t = ( 2 a 0 + a 1 + 2 a 1 t ) e 2 t , { \frac { { d x } } { { d t } } } = { { a _ 1 } { e^ { 2 t } } + 2 \left ( { { a _ 0 } + { a _ 1 } t } \right ) { e ^ { 2 t } } } = { \left ( { 2 { a _ 0 } + { a _ 1 } + 2 { a _ 1 } t } \right ) { e ^ { 2 t } } , } d t d x = a 1 e 2 t + 2 ( a 0 + a 1 t ) e 2 t = ( 2 a 0 + a 1 + 2 a 1 t ) e 2 t ,
d y d t = b 1 e 2 t + 2 ( b 0 + b 1 t ) e 2 t = ( 2 b 0 + b 1 + 2 b 1 t ) e 2 t . { \frac { { d y } }{ { d t } } } = { { b _ 1 } { e ^ { 2 t } } + 2 \left ( { { b _ 0 } + { b _ 1 } t } \right ) { e ^ { 2 t } } } = { \left ( { 2 { b _ 0 } + { b _ 1 } + 2 { b _ 1 } t } \right ) { e ^ { 2 t } } . } d t d y = b 1 e 2 t + 2 ( b 0 + b 1 t ) e 2 t = ( 2 b 0 + b 1 + 2 b 1 t ) e 2 t .
با جایگذاری توابع x x x y y y
{ ( 2 a 0 + a 1 + 2 a 1 t ) e 2 t = ( a 0 + a 1 t ) e 2 t − ( b 0 + b 1 t ) e 2 t ( 2 b 0 + b 1 + 2 b 1 t ) e 2 t = ( a 0 + a 1 t ) e 2 t + 3 ( b 0 + b 1 t ) e 2 t \left \{ \begin {array} { l } { \left ( { 2 { a _ 0 } + { a _ 1 } + 2 { a _ 1 } t } \right ){ e ^ { 2 t } } } = { \left ( { { a _ 0 } + { a _ 1 } t } \right ){ e ^ { 2 t } } } - { \left ( { { b _ 0 } + { b _ 1 } t } \right ){ e ^ { 2 t } } } \\ { \left ( { 2 { b _ 0 } + { b _ 1 } + 2 { b _ 1 } t } \right ){ e ^ { 2 t } } } = { \left ( { { a _ 0 } + { a _ 1 } t } \right ){ e ^ { 2 t } } } + { 3 \left ( { { b _ 0 } + { b _ 1 } t } \right ){ e ^ { 2 t } } } \end {array} \right . { ( 2 a 0 + a 1 + 2 a 1 t ) e 2 t = ( a 0 + a 1 t ) e 2 t − ( b 0 + b 1 t ) e 2 t ( 2 b 0 + b 1 + 2 b 1 t ) e 2 t = ( a 0 + a 1 t ) e 2 t + 3 ( b 0 + b 1 t ) e 2 t
اکنون با تقسیم دو طرف تساوی بر e 2 t e ^ { 2 t } e 2 t
$$ { \left \{ \begin {array} { l }<br />
2 { a _ 0 } + { a _ 1 } = { a _ 0 } – { b _ 0 } \\<br />
2 { a _ 1 } = { a _ 1 } – { b _ 1 } \\<br />
2 { b _ 0 } + { b _ 1 } = { a _ 0 } + 3 { b _ 0 } \\<br />
2 { b _ 1 } = { a _ 1 } + 3 { b _ 1 }<br />
\end {array} \right . , \; \; } \Rightarrow<br />
{ \left \{ { \begin {array} { * { 2 0 } { l } }<br />
{ { a _ 0 } + { a _ 1 } + { b _ 0 } = 0 } \\<br />
{ { a _ 1 } + { b _ 1 } = 0 } \\<br />
{ { a _ 0 } + { b _ 0 } – { b _ 1 } = 0 } \\<br />
{ { a _ 1 } + { b _ 1 } = 0 }<br />
\end {array} } \right . . } $$
در این دستگاه، فقط دو معادله مستقل وجود دارد. ضرایب مستقل a 0 = C 1 a_ 0 = C _ 1 a 0 = C 1 a 1 = C 2 a _ 1 = C _ 2 a 1 = C 2 b 0 b _ 0 b 0 b 1 b_ 1 b 1 C 1 C_ 1 C 1 C 2 C_ 2 C 2
C 1 + C 2 + b 0 = 0 , ⇒ b 0 = – C 1 – C 2 , C 2 + b 1 = 0 , ⇒ b 1 = – C 2 . { { C _ 1 } + { C _ 2 } + { b _ 0 } = 0 , \; \; } \Rightarrow { { b _ 0 } = – { C _ 1 } – { C _ 2 } , } \\ { { C _ 2 } + { b _ 1 } = 0 , \; \; } \Rightarrow { { b _ 1 } = – { C _ 2 } . } C 1 + C 2 + b 0 = 0 , ⇒ b 0 = – C 1 – C 2 , C 2 + b 1 = 0 , ⇒ b 1 = – C 2 .
بنابراین، جواب عمومی به فرم زیر خواهد بود:
$$ { \mathbf { X } \left ( t \right ) = \left [ { \begin {array} { * { 2 0 } { c } }<br />
x \\<br />
y<br />
\end {array} } \right ] } = { { e ^ { 2 t } } \left [ { \begin {array} { * { 2 0 } { c } }<br />
{ { a _ 0 } + { a _ 1 } t } \\<br />
{ { b _ 0 } + { b _ 1 } t }<br />
\end {array} } \right ] }<br />
= { { e ^ { 2 t } } \left [ { \begin {array} { * { 2 0 } { c } }<br />
{ { C _ 1 } + { C _ 2 } t } \\<br />
{ – { C _ 1 } – { C _ 2 } – { C _ 2 } t }<br />
\end {array} } \right ] . } $$
و میتوان آن را بهسادگی به فرم برداری زیر نوشت:
$$ \begin {align*} \mathbf { X } \left ( t \right ) & = \left [ { \begin {array} { * { 2 0 } { c } } x \\ y \end {array} } \right ] = { { C _ 1 } { e ^ { 2 t } } \left [ { \begin {array} { * { 2 0 } { c } } 1 \\ { – 1 } \end {array} } \right ] } + { { C _ 2 } { e ^ { 2 t } } \left [ { \begin {array} { * { 2 0 } { c } } t \\ { – 1 – t } \end {array} } \right ] } \\ & = { { C _ 1 } { e ^ { 2 t } } \left [ { \begin {array} { * { 2 0 } { c } } 1 \\ { – 1 } \end {array} } \right ] } + { { C _ 2 } { e ^ { 2 t} } \left ( { \left [ { \begin {array} { * { 2 0 } { c } } 0 \\ { – 1 } \end {array} } \right ] + t \left [ { \begin {array} { * { 2 0 } { c } } 1 \\ { – 1 } \end {array} } \right ] } \right ) . } \end {align*} $$
نمونه سوال معادلات دیفرانسیل ۲۵
پاسخ عمومی معادله x 2 y ′ ′ – 4 x y ′ + 6 y = 0 { x ^ 2 } y ^ { \prime \prime } – 4 x y ^ { \prime } + 6 y = 0 x 2 y ′′ –4 x y ′ + 6 y = 0 y 1 = x 2 { y _ 1 } = { x ^ 2 } y 1 = x 2
حل سوال ۲۵: به منظور پاسخ به این سوال در ابتدا y 1 y_1 y 1 y 2 y_2 y 2
$$ {\begin {align*} W \left( x \right) & = {W_{{y_1},{y_2}}}\left( x \right)<br />
= {\left| {\begin{array}{*{20} { c } } { { y _1 } } & { { y _2 } } \\<br />
{ { y ^ { \prime }_1}}& { { y ^ { \prime } _ 2 } } \end {array} } \right| } \\ & = { { W _ 0 } \left ( x \right)\exp \left( { – \int \limits _ {{ x _ 0 } } ^ x { \frac { { { a _1 } \left( t \right ) } } { { {a _ 0 } \left ( t \right ) } } d t } } \right ) } \end {align*}} $$
انتگرال رابطه بالا بهصورت زیر در خواهد آمد:
∫ x 0 x a 1 ( t ) a 0 ( t ) d t = ∫ x 0 x ( – 4 t t 2 ) d t = ( – 4 ln t ) ∣ x 0 x = – 4 ln x + 4 ln x 0 = – ln x 4 + ln x 0 4 = – ln x 4 x 0 4 \begin {align*} \int\limits _ { { x_0 } } ^ x { \frac { { {a _ 1 } \left( t \right)}}{{{a_0}\left( t \right ) }} d t } & = { \int \limits _ { { x _ 0 } } ^ x { \left ( { \frac { { – 4 t } } { { { t ^ 2} } } } \right)dt} } \\ & = {\left. {\left( { – 4 \ln t } \right ) } \right|_ { { x _0 } } ^ x } \\ & = { – 4\ln x + 4 \ln { x _ 0 } } \\ & = { – \ln { x ^ 4 } + \ln x_0^4 } = { – \ln \frac { { { x ^ 4 }} } { { x _0 ^ 4 } } } \end {align*} x 0 ∫ x a 0 ( t ) a 1 ( t ) d t = x 0 ∫ x ( t 2 –4 t ) d t = ( –4 ln t ) ∣ x 0 x = –4 ln x + 4 ln x 0 = – ln x 4 + ln x 0 4 = – ln x 0 4 x 4
در نتیجه، رونسکین نیز بهشکل زیر بهدست میآید:
$$ \begin {align*} {\left| {\begin{array}{*{20}{c}} { { y _ 1 } } & { { y _2 } } \\<br />
{{y ^ { \prime } _ 1 } } & { { y ^{\prime} _ 2 } } \end{array}} \right| } & = {{W_0}\left( x \right)\exp \left ( {\ln \frac { { { x ^ 4} } } {{ x _0 ^ 4 } } } \right) } \\ & = { \frac { { { W_0}\left( x \right)}}{{x_0^4}}{ x ^ 4 } } = { { C _1 } { x ^ 4 } } \end {align*} $$
با توجه به اینکه y 1 y_1 y 1 y 2 y_2 y 2
$$ \require {cancel} \begin {align*} \left. { { y ^ { \prime } _ 2 } { y_ 1 } – { y _2 } { y ^ { \prime } _ 1 } = { C _ 1 } { x ^ 4 } } \right|:y _ 1 ^ 2 \ \\~\\ \Rightarrow {\frac { { { y ^ { \prime } _2 } { y _ 1 } – { y _2 } { y ^ { \prime } _ 1} } } { { y _ 1 ^ 2} } = \frac { { {C _ 1 } { x ^4 } } } { {y _ 1 ^ 2 } } } \\~\\ \Rightarrow { { \left( {\frac { { { y _ 2 } } } { { { y_ 1 } } } } \right ) ^ \prime } } = {\frac { {{ C _ 1 } { x^ 4 } } } { { y _ 1 ^ 2 } } } = { \frac { { { C _ 1 } \cancel { x ^ 4}} } { { \cancel { x ^ 4 }} } } = { { C _ 1 } } \end {align*} $$
در نتیجه تابع y 2 y_2 y 2
y 2 y 1 = C 1 x + C 2 ⇒ y 2 = y 1 ( C 1 x + C 2 ) x 2 ( C 1 x + C 2 ) = C 1 x 3 + C 2 x 2 \begin {align*} \frac { { { y_ 2 } } } { { { y _ 1 } } } & = {C_1}x + {C_2} \;\; \Rightarrow { y _ 2 } \\ & = { y _ 1 } \left ( { { C _1 } x + { C _ 2 } } \right ) { { x ^ 2 } \left ( { { C_ 1 } x + { C _ 2 } } \right ) } \\ & = { { C_ 1 } { x ^ 3 } + { C _ 2 }{ x ^2 } } \end {align*} y 1 y 2 = C 1 x + C 2 ⇒ y 2 = y 1 ( C 1 x + C 2 ) x 2 ( C 1 x + C 2 ) = C 1 x 3 + C 2 x 2
همانطور که میبینیم، تابع y 2 y_2 y 2 y 1 y_1 y 1 y 2 y_2 y 2
نمونه سوال معادلات دیفرانسیل ۲۶
پاسخ معادله دیفرانسیل زیر را در بازه x > 0 x > 0 x > 0
x 2 y ′ ′ + 3 x y ′ + 4 y = 0 { x ^ 2 } y ^ { \prime\prime } + 3 x y ^ { \prime } + 4 y = 0 x 2 y ′′ + 3 x y ′ + 4 y = 0
حل سوال ۲۶: معادله مشخصه برای این معادله دیفرانسیل اویلر بهصورت زیر است:
r ( r − 1 ) + 3 r + 4 = 0 r 2 + 2 r + 4 = 0 ⇒ r 1 , 2 = − 1 ± 3 i \begin {align*} r \left ( { r - 1 } \right ) + 3 r + 4 & = 0 \\ { r ^ 2 } + 2 r + 4 & = 0 \hspace {0.25in} \Rightarrow \hspace {0.25in} { r _ { 1 , 2 } } = - 1 \pm \sqrt 3 \, i \end {align*} r ( r − 1 ) + 3 r + 4 r 2 + 2 r + 4 = 0 = 0 ⇒ r 1 , 2 = − 1 ± 3 i
جوابهای این معادله مختلط هستند. بنابراین، جواب عمومی معادله بهصورت زیر است:
y ( x ) = c 1 x − 1 cos ( 3 ln x ) + c 2 x − 1 sin ( 3 ln x ) y \left ( x \right ) = { c _ 1 } { x ^ { - 1 } } \cos \left ( { \sqrt 3 \ln x } \right ) + { c _ 2 } { x ^ { - 1 } } \sin \left ( { \sqrt 3 \ln x } \right ) y ( x ) = c 1 x − 1 cos ( 3 ln x ) + c 2 x − 1 sin ( 3 ln x )
معادله در همه بازهها پاسخ دارد. در واقع، x x x ∣ x ∣ |x| ∣ x ∣ x x x
نمونه سوال معادلات دیفرانسیل ۲۷
معادله x 2 y ′ ′ – 2 x y ’ + 2 y = 6 x 2 + 4 ln x { x ^ 2 } y ^ { \prime \prime } – 2 x y’ + 2 y = 6 { x ^ 2 } + 4 \ln x x 2 y ′′ –2 x y ’ + 2 y = 6 x 2 + 4 ln x x > 0 x > 0 x > 0
حل سوال ۲۷: این معادله یک معادله اویلر ناهمگن است. برای حل آن، ابتدا معادله همگن را حل میکنیم:
x 2 y ′ ′ – 2 x y ’ + 2 y = 0 { { x ^ 2 } y ^ { \prime \prime } – 2 x y’ + 2 y } = { 0 } x 2 y ′′ –2 x y ’ + 2 y = 0
با قرار دادن x = e t x = e ^ t x = e t
d 2 y d t 2 – 3 d y d t + 2 y = 0 { \frac { { { d ^ 2 } y } } { { d { t ^ 2 } } } – 3 \frac { { d y } } { { d t } } } + { 2 y } = { 0 } d t 2 d 2 y –3 d t d y + 2 y = 0
اکنون معادله مشخصه و ریشههای آن را تعیین میکنیم:
k 2 – 3 k + 2 = 0 , ⇒ D = 9 – 4 ⋅ 2 = 1 , ⇒ k 1 , 2 = 3 ± 1 2 = 2 , 1. { { k ^ 2 } – 3 k + 2 = 0 , \; \; } \Rightarrow { D = 9 – 4 \cdot 2 = 1 , \; \; } \Rightarrow { { k _ { 1 , 2 } } = \frac { { 3 \pm 1 } } { 2 } = 2 , 1 . } k 2 –3 k + 2 = 0 , ⇒ D = 9–4 ⋅ 2 = 1 , ⇒ k 1 , 2 = 2 3 ± 1 = 2 , 1.
همچنین، جواب عمومی y 0 ( t ) y _ 0 ( t) y 0 ( t )
y 0 ( t ) = C 1 e 2 t + C 2 e t . { { y _ 0 } \left ( t \right ) } = { { C _ 1 } { e ^ { 2 t } } + { C _ 2 } { e ^ t } . } y 0 ( t ) = C 1 e 2 t + C 2 e t .
اکنون میتوانیم معادله ناهمگن را برحسب t t t
d 2 y d t 2 – 3 d y d t + 2 y = 6 e 2 t + 4 ln ( e t ) , ⇒ d 2 y d t 2 – 3 d y d t + 2 y = 6 e 2 t + 4 t { { \frac { { { d ^ 2 } y } } { { d { t ^ 2 } } } – 3 \frac { { d y } } { { d t } } + 2 y } = { 6 { e ^ { 2 t } } + 4 \ln \left ( { { e ^ t } } \right ) , \; \; } } \\ \Rightarrow { { \frac { { { d ^ 2 } y } }{ { d { t ^ 2 } } } – 3 \frac { { d y } } { { d t } } + 2 y } = { 6 { e ^ { 2 t } } + 4 t } } d t 2 d 2 y –3 d t d y + 2 y = 6 e 2 t + 4 ln ( e t ) , ⇒ d t 2 d 2 y –3 d t d y + 2 y = 6 e 2 t + 4 t
ضریب توان t t t
y 1 ( t ) = a t e 2 t + b t + c , { y _ 1 } \left ( t \right ) = a t { e ^ { 2 t } } + b t + c , y 1 ( t ) = a t e 2 t + b t + c ,
که در آن، a a a b b b c c c
مشتقات این تابع به صورت زیر هستند:
d y 1 d t = a e 2 t + 2 a t e 2 t + b , { \frac { { d { y _ 1 } } } { { d t } } } = { a {e ^ { 2 t } } + 2 a t { e ^ { 2 t } } + b , } d t d y 1 = a e 2 t + 2 a t e 2 t + b ,
d 2 y 1 d t 2 = 2 a e 2 t + 2 a e 2 t + 4 a t e 2 t = 4 a e 2 t + 4 a t e 2 t . { \frac { { { d ^ 2 } { y _ 1 } } } { { d { t ^ 2 } } } } = { 2 a { e ^ { 2 t } } + 2 a { e ^ { 2 t } } + 4 a t { e ^ { 2 t } } } = { 4 a { e ^ { 2 t } } + 4 a t { e ^ { 2 t } } . } d t 2 d 2 y 1 = 2 a e 2 t + 2 a e 2 t + 4 a t e 2 t = 4 a e 2 t + 4 a t e 2 t .
با قرار دادن این مشتقات در معادله ناهمگن، خواهیم داشت:
$$ \require {cancel} { 4 a { e ^ { 2 t } } + 4 a t { e ^ { 2 t } } }<br />
– { 3 \left ( { a { e ^ { 2 t } } + 2 a t { e ^ { 2 t } } + b } \right ) }<br />
+ { 2 \left ( { a t { e ^ { 2 t } } + b t + c } \right ) }<br />
= { 6 { e ^ { 2 t } } + 4 t , } \\ { \Rightarrow 4 a { e ^ { 2 t } } + \cancel { 4 a t { e ^ { 2 t } } } – 3a { e ^ { 2 t } } }<br />
– { \cancel { 6 a t { e ^ { 2 t } } } – 3 b }<br />
+ { \cancel { 2 a t { e ^ { 2 t } } } + 2 b t + 2 c }<br />
= { 6 { e ^ { 2 t } } + 4 t , } $$
رابطه آخر تحلیلی است، یعنی برای همه مقادیر t t t
{ a = 6 2 b = 4 – 3 b + 2 c = 0 , ⇒ { a = 6 b = 2 c = 3 . { \left \{ \begin {array} { l } a = 6 \\ 2 b = 4 \\ – 3 b + 2 c = 0 \end {array} \right . , \; \; } \Rightarrow { \left \{ \begin {array} { l } a = 6 \\ b = 2 \\ c = 3 \end {array} \right . . } ⎩ ⎨ ⎧ a = 6 2 b = 4 –3 b + 2 c = 0 , ⇒ ⎩ ⎨ ⎧ a = 6 b = 2 c = 3 .
بنابراین، یک جواب خصوصی معادله ناهمگن به صورت زیر است:
y 1 ( t ) = 6 t e 2 t + 2 t + 3. { { y _ 1 } \left ( t \right ) } = { 6 t { e ^ { 2 t } } + 2 t + 3 . } y 1 ( t ) = 6 t e 2 t + 2 t + 3.
اکنون میتوانیم جواب عمومی معادله اویلر ناهمگن را بنویسیم:
y ( t ) = y 0 ( t ) + y 1 ( t ) = C 1 e 2 t + C 2 e t + 6 t e 2 t + 2 t + 3. { y \left ( t \right ) = { y _ 0 } \left ( t \right ) + { y _ 1 } \left ( t \right ) } = { { C _ 1 } { e ^ { 2 t } } + { C _ 2 }{ e ^ t } } + { 6 t { e ^ { 2 t } } } + { 2 t + 3 . } y ( t ) = y 0 ( t ) + y 1 ( t ) = C 1 e 2 t + C 2 e t + 6 t e 2 t + 2 t + 3.
از آنجا که t = ln x t = \ln x t = ln x
y ( x ) = C 1 x 2 + C 2 x + 6 x 2 ln x + 2 ln x + 3 , { y \left ( x \right ) } = { { C _ 1 } { x^ 2 } + { C _ 2 } x } + { 6 { x ^ 2 } \ln x } + { 2 \ln x + 3 , } y ( x ) = C 1 x 2 + C 2 x + 6 x 2 ln x + 2 ln x + 3 ,
که در آن، C 1 C _ 1 C 1 C 2 C _ 2 C 2
نمونه سوال معادلات دیفرانسیل ۲۸
مسئله مقدار اولیه زیر را حل کنید.
y ′ ′ ′ − 4 y ′ ′ = 4 t + 3 u 6 ( t ) e 30 − 5 t , y ( 0 ) = − 3 y ′ ( 0 ) = 1 y ′ ′ ( 0 ) = 4 y''' - 4y'' = 4t + 3{u_6}\left( t \right){{\bf{e}}^{30 - 5t}},\hspace{0.25in}y\left( 0 \right) = - 3\,\,\,y'\left( 0 \right) = 1\,\,\,\,\,y''\left( 0 \right) = 4 y ′′′ − 4 y ′′ = 4 t + 3 u 6 ( t ) e 30 − 5 t , y ( 0 ) = − 3 y ′ ( 0 ) = 1 y ′′ ( 0 ) = 4
حل سوال ۲۸: ابتدا باید بررسی کنیم جابهجایی زمانی تابع پله u ( t ) u(t) u ( t )
y ′ ′ ′ − 4 y ′ ′ = 4 t + 3 u 6 ( t ) e − 5 ( t − 6 ) y''' - 4y'' = 4t + 3{u_6}\left( t \right){{\bf{e}}^{ - 5\left( {t - 6} \right)}} y ′′′ − 4 y ′′ = 4 t + 3 u 6 ( t ) e − 5 ( t − 6 )
میبینیم که جابهجایی e − 5 t {{\bf{e}}^{ - 5t}} e − 5 t
L { y ′ ′ ′ } = s 3 Y ( s ) − s 2 y ( 0 ) − s y ′ ( 0 ) − y ′ ′ ( 0 ) \mathcal{L}\left\{ {y'''} \right\} = {s^3}Y\left( s \right) - {s^2}y\left( 0 \right) - sy'\left( 0 \right) - y''\left( 0 \right) L { y ′′′ } = s 3 Y ( s ) − s 2 y ( 0 ) − s y ′ ( 0 ) − y ′′ ( 0 )
بنابراین، داریم:
s 3 Y ( s ) − s 2 y ( 0 ) − s y ′ ( 0 ) − y ′ ′ ( 0 ) − 4 ( s 2 Y ( s ) − s y ( 0 ) − y ′ ( 0 ) ) = 4 s 2 + 3 e − 6 s s + 5 ( s 3 − 4 s 2 ) Y ( s ) + 3 s 2 − 13 s = 4 s 2 + 3 e − 6 s s + 5 ( s 3 − 4 s 2 ) Y ( s ) = 4 s 2 − 3 s 2 + 13 s + 3 e − 6 s s + 5 ( s 3 − 4 s 2 ) Y ( s ) = 4 − 3 s 4 + 13 s 3 s 2 + 3 e − 6 s s + 5 Y ( s ) = 4 − 3 s 4 + 13 s 3 s 4 ( s − 4 ) + 3 e − 6 s s 2 ( s − 4 ) ( s + 5 ) Y ( s ) = F ( s ) + 3 e − 6 s G ( s ) \begin{align*}{s^3}Y\left( s \right) - {s^2}y\left( 0 \right) - sy'\left( 0 \right) - y''\left( 0 \right) - 4\left( {{s^2}Y\left( s \right) - sy\left( 0 \right) - y'\left( 0 \right)} \right) & = \frac{4}{{{s^2}}} + \frac{{3{{\bf{e}}^{ - 6s}}}}{{s + 5}}\\ \hspace{0.25in}\hspace{0.25in}\left( {{s^3} - 4{s^2}} \right)Y\left( s \right) + 3{s^2} - 13s & = \frac{4}{{{s^2}}} + \frac{{3{{\bf{e}}^{ - 6s}}}}{{s + 5}}\\ \hspace{0.25in}\hspace{0.25in}\left( {{s^3} - 4{s^2}} \right)Y\left( s \right) & = \frac{4}{{{s^2}}} - 3{s^2} + 13s + \frac{{3{{\bf{e}}^{ - 6s}}}}{{s + 5}}\\ \hspace{0.25in}\hspace{0.25in}\left( {{s^3} - 4{s^2}} \right)Y\left( s \right) & = \frac{{4 - 3{s^4} + 13{s^3}}}{{{s^2}}} + \frac{{3{{\bf{e}}^{ - 6s}}}}{{s + 5}}\\ \hspace{0.25in}\hspace{0.25in}\hspace{0.25in}\hspace{0.25in}\,\,\,\,\,\,\,\,Y\left( s \right) & = \frac{{4 - 3{s^4} + 13{s^3}}}{{{s^4}\left( {s - 4} \right)}} + \frac{{3{{\bf{e}}^{ - 6s}}}}{{{s^2}\left( {s - 4} \right)\left( {s + 5} \right)}}\\ \hspace{0.25in}\hspace{0.25in}\,\,\,\,\,\,\,\,\,\,\,Y\left( s \right) & = F\left( s \right) + 3{{\bf{e}}^{ - 6s}}G\left( s \right)\end{align*} s 3 Y ( s ) − s 2 y ( 0 ) − s y ′ ( 0 ) − y ′′ ( 0 ) − 4 ( s 2 Y ( s ) − sy ( 0 ) − y ′ ( 0 ) ) ( s 3 − 4 s 2 ) Y ( s ) + 3 s 2 − 13 s ( s 3 − 4 s 2 ) Y ( s ) ( s 3 − 4 s 2 ) Y ( s ) Y ( s ) Y ( s ) = s 2 4 + s + 5 3 e − 6 s = s 2 4 + s + 5 3 e − 6 s = s 2 4 − 3 s 2 + 13 s + s + 5 3 e − 6 s = s 2 4 − 3 s 4 + 13 s 3 + s + 5 3 e − 6 s = s 4 ( s − 4 ) 4 − 3 s 4 + 13 s 3 + s 2 ( s − 4 ) ( s + 5 ) 3 e − 6 s = F ( s ) + 3 e − 6 s G ( s )
اکنون تبدیل لاپلاس جواب مورد نظر را در اختیار داریم. برای بهدست آوردن جواب، باید F ( s ) F(s) F ( s ) G ( s ) G(s) G ( s )
F ( s ) = 4 − 3 s 4 + 13 s 3 s 4 ( s − 4 ) = 17 64 s − 4 − 209 64 s − 1 16 s 2 − 1 4 ( 2 ! 2 ! ) s 3 − 1 ( 3 ! 3 ! ) s 4 f ( t ) = 17 64 e 4 t − 209 64 − 1 16 t − 1 8 t 2 − 1 6 t 3 \begin{align*}F\left( s \right) & = \frac{{4 - 3{s^4} + 13{s^3}}}{{{s^4}\left( {s - 4} \right)}} = \frac{{\frac{{17}}{{64}}}}{{s - 4}} - \frac{{\frac{{209}}{{64}}}}{s} - \frac{{\frac{1}{{16}}}}{{{s^2}}} - \frac{{\frac{1}{4}\left( {\frac{{2!}}{{2!}}} \right)}}{{{s^3}}} - \frac{{1\left( {\frac{{3!}}{{3!}}} \right)}}{{{s^4}}}\\ f\left( t \right) & = \frac{{17}}{{64}}{{\bf{e}}^{4t}} - \frac{{209}}{{64}} - \frac{1}{{16}}t - \frac{1}{8}{t^2} - \frac{1}{6}{t^3}\end{align*} F ( s ) f ( t ) = s 4 ( s − 4 ) 4 − 3 s 4 + 13 s 3 = s − 4 64 17 − s 64 209 − s 2 16 1 − s 3 4 1 ( 2 ! 2 ! ) − s 4 1 ( 3 ! 3 ! ) = 64 17 e 4 t − 64 209 − 16 1 t − 8 1 t 2 − 6 1 t 3
G ( s ) = 1 s 2 ( s − 4 ) ( s + 5 ) = 1 144 s − 4 − 1 225 s + 5 − 1 400 s − 1 20 s 2 g ( t ) = 1 144 e 4 t − 1 225 e − 5 t − 1 400 − 1 20 t \begin{align*}G\left( s \right) & = \frac{1}{{{s^2}\left( {s - 4} \right)\left( {s + 5} \right)}} = \frac{{\frac{1}{{144}}}}{{s - 4}} - \frac{{\frac{1}{{225}}}}{{s + 5}} - \frac{{\frac{1}{{400}}}}{s} - \frac{{\frac{1}{{20}}}}{{{s^2}}}\\ g\left( t \right) & = \frac{1}{{144}}{{\bf{e}}^{4t}} - \frac{1}{{225}}{{\bf{e}}^{ - 5t}} - \frac{1}{{400}} - \frac{1}{{20}}t\end{align*} G ( s ) g ( t ) = s 2 ( s − 4 ) ( s + 5 ) 1 = s − 4 144 1 − s + 5 225 1 − s 400 1 − s 2 20 1 = 144 1 e 4 t − 225 1 e − 5 t − 400 1 − 20 1 t
اکنون میتوانیم جواب معادله دیفرانسیل را بهصورت زیر بنویسیم که در آن، f ( t ) f(t) f ( t ) g ( t ) g(t) g ( t )
Y ( s ) = F ( s ) + 3 e − 6 s G ( s ) ⇒ y ( t ) = f ( t ) + 3 u 6 ( t ) g ( t − 6 ) Y\left( s \right) = F\left( s \right) + 3{{\bf{e}}^{ - 6s}}G\left( s \right)\hspace{0.25in}\hspace{0.25in} \Rightarrow \hspace{0.25in}\hspace{0.25in}y\left( t \right) = f\left( t \right) + 3{u_6}\left( t \right)g\left( {t - 6} \right) Y ( s ) = F ( s ) + 3 e − 6 s G ( s ) ⇒ y ( t ) = f ( t ) + 3 u 6 ( t ) g ( t − 6 )
نمونه سوال معادلات دیفرانسیل ۲۹
جواب معادله دیفرانسیل ( x 2 + 4 ) y ’ = 2 x y \left( {{x^2} + 4} \right)y’ = 2xy ( x 2 + 4 ) y ’ = 2 x y
حل سوال ۲۹: معادله را بهفرم زیر مینویسیم:
( x 2 + 4 ) d y = 2 x y d x . \left ( { { x ^ 2 } + 4 } \right ) d y = 2 x y d x . ( x 2 + 4 ) d y = 2 x y d x .
هردو سمت معادله را بر ( x 2 + 4 ) y \left( {{x^2} + 4} \right)y ( x 2 + 4 ) y
d y y = 2 x d x ( x 2 + 4 ) . \frac { { d y } } { y } = \frac { { 2 x d x } } { { \left ( { { x ^ 2 } + 4 } \right ) } } . y d y = ( x 2 + 4 ) 2 x d x .
مشخص است که برای همه x x x x 2 + 4 ≠ 0 {{x^2} + 4} \ne 0 x 2 + 4 = 0 y = 0 y = 0 y = 0 y = 0 y=0 y = 0 d y = 0 dy=0 d y = 0 y = 0 y=0 y = 0
اکنون از معادله انتگرال میگیریم:
∫ d y y = ∫ 2 x d x ( x 2 + 4 ) + C , ⇒ ln ∣ y ∣ = ∫ d ( x 2 ) x 2 + 4 + C . { { \int { \frac { { d y } } { y } } } = { \int { \frac { { 2 x d x } } { { \left( { { x ^ 2 } + 4 } \right ) } } } } + { C , \;\; } } \Rightarrow { { \ln \left | y \right | } = { \int { \frac { { d \left ( { { x ^ 2 } } \right ) } } { { { x ^ 2 } + 4 } } } } + { C . } } ∫ y d y = ∫ ( x 2 + 4 ) 2 x d x + C , ⇒ ln ∣ y ∣ = ∫ x 2 + 4 d ( x 2 ) + C .
میدانیم که d ( x 2 ) d\left( {{x^2}} \right) d ( x 2 )
ln ∣ y ∣ = ∫ d ( x 2 + 4 ) x 2 + 4 + C , ⇒ ln ∣ y ∣ = ln ( x 2 + 4 ) + C . { \ln \left | y \right | = \int { \frac { { d \left ( { { x ^ 2 } + 4 } \right ) } } { { { x ^ 2 } + 4 } } } + C , \;\; } \Rightarrow { \ln \left | y \right | = \ln \left ( { { x ^ 2 } + 4 } \right ) + C . } ln ∣ y ∣ = ∫ x 2 + 4 d ( x 2 + 4 ) + C , ⇒ ln ∣ y ∣ = ln ( x 2 + 4 ) + C .
ثابت C C C ln C 1 \ln {C_1} ln C 1 C 1 > 0 {C_1} \gt 0 C 1 > 0
ln ∣ y ∣ = ln ( x 2 + 4 ) + ln C 1 , ⇒ ln ∣ y ∣ = ln ( C 1 ( x 2 + 4 ) ) , ⇒ ∣ y ∣ = C 1 ( x 2 + 4 ) , ⇒ y = ± C 1 ( x 2 + 4 ) . { \ln \left | y \right | = \ln \left ( { { x ^ 2 } + 4 } \right ) + \ln { C _ 1 } ,\;\; }\Rightarrow { \ln \left | y \right | = \ln \left ( { { C _ 1 } \left ( { { x ^ 2 } + 4 } \right ) } \right ) , \;\; }\\ \Rightarrow { \left | y \right | = { C _ 1 } \left ( { { x ^ 2 } + 4 } \right ) , \;\; } \Rightarrow { y = \pm { C _ 1 } \left ( { { x ^ 2 } + 4 } \right ) . } ln ∣ y ∣ = ln ( x 2 + 4 ) + ln C 1 , ⇒ ln ∣ y ∣ = ln ( C 1 ( x 2 + 4 ) ) , ⇒ ∣ y ∣ = C 1 ( x 2 + 4 ) , ⇒ y = ± C 1 ( x 2 + 4 ) .
بنابراین، جواب معادله دیفرانسیل بهصورت زیر خواهد بود:
y = ± C 1 ( x 2 + 4 ) , y = 0 , , C 1 > 0. { y = \pm { C _ 1 } \left ( { { x ^ 2 } + 4 } \right ) , \;\;}\kern-0.3pt { y = 0 , \;\;}\kern-0.3pt { \text{,}\;\;}\kern-0.3pt { { C _ 1 } \gt 0.} y = ± C 1 ( x 2 + 4 ) , y = 0 , , C 1 > 0.
این جواب را میتوان سادهتر کرد. درواقع، اگر از ثابت دلخواه C C C − ∞ -\infty − ∞ ∞ \infty ∞
y = C ( x 2 + 4 ) . y = C \left ( { { x ^ 2 } + 4 } \right ) . y = C ( x 2 + 4 ) .
اگر C = 0 C = 0 C = 0 y = 0 y=0 y = 0
حل: معادله مربوط به این مثال، شبیه حالت ۲ است که سمت راست آن فقط به متغیر y y y p = y ’ p = y’ p = y ’
d p d y p = 1 4 y , ⇒ 2 p d p = d y 2 y , ⇒ ∫ 2 p d p = ∫ d y 2 y , ⇒ p 2 = y + C 1 , {\frac{{dp}}{{dy}}p = \frac{1}{{4\sqrt y }},\;\;}\Rightarrow {2pdp = \frac{{dy}}{{2\sqrt y }},\;\;}\\\Rightarrow {\int {2pdp} = \int {\frac{{dy}}{{2\sqrt y }}} ,\;\;}\Rightarrow {{p^2} = \sqrt y + {C_1},} d y d p p = 4 y 1 , ⇒ 2 p d p = 2 y d y , ⇒ ∫ 2 p d p = ∫ 2 y d y , ⇒ p 2 = y + C 1 ,
که در آن، C 1 C_1 C 1
با جذر گرفتن از دو سمت معادله، تابع p ( y ) p(y) p ( y )
p = ± y + C 1 . p = \pm \sqrt {\sqrt y + {C_1}} . p = ± y + C 1 .
اکنون با دانستن y ’ = p y’ = p y ’ = p
y ’ = ± y + C 1 , ⇒ d y d x = ± y + C 1 . {y’ = \pm \sqrt {\sqrt y + {C_1}} ,\;\;}\Rightarrow {\frac{{dy}}{{dx}} = \pm \sqrt {\sqrt y + {C_1}} .} y ’ = ± y + C 1 , ⇒ d x d y = ± y + C 1 .
با جداسازی متغیرها و انتگرالگیری، داریم:
d y y + C 1 = ± d x , ⇒ ∫ d y y + C 1 = ± ∫ d x . {\frac{{dy}}{{\sqrt {\sqrt y + {C_1}} }} = \pm dx,\;\;}\Rightarrow {\int {\frac{{dy}}{{\sqrt {\sqrt y + {C_1}} }}} = \pm \int {dx} .} y + C 1 d y = ± d x , ⇒ ∫ y + C 1 d y = ± ∫ d x .
برای محاسبه انتگرال سمت چپ، از تغییر متغیر زیر استفاده میکنیم:
y + C 1 = z , ⇒ d z = d y 2 y , ⇒ d y = 2 y d z = 2 ( z – C 1 ) d z . {\sqrt y + {C_1} = z,\;\;}\Rightarrow {dz = \frac{{dy}}{{2\sqrt y }},\;\;}\\\Rightarrow {dy = 2\sqrt y dz }={ 2\left( {z – {C_1}} \right)dz.} y + C 1 = z , ⇒ d z = 2 y d y , ⇒ d y = 2 y d z = 2 ( z – C 1 ) d z .
در نتیجه، انتگرال سمت چپ برابر است با:
∫ d y y + C 1 = ∫ 2 ( z – C 1 ) d z z = 2 ∫ ( z z – C 1 z ) d z = 2 ∫ ( z 1 2 – C 1 z – 1 2 ) d z = 2 ( z 3 2 3 2 – C 1 z 1 2 1 2 ) = 4 3 z 3 2 – 4 C 1 z 1 2 = 4 3 ( y + C 1 ) 3 − 4 C 1 y + C 1 . {\int {\frac{{dy}}{{\sqrt {\sqrt y + {C_1}} }}} } = {\int {\frac{{2\left( {z – {C_1}} \right)dz}}{{\sqrt z }}} } = {2\int {\left( {\frac{z}{{\sqrt z }} – \frac{{{C_1}}}{{\sqrt z }}} \right)dz} } \\ = {2\int {\left( {{z^{ \frac{1}{2}\normalsize}} – {C_1}{z^{ – \frac{1}{2}\normalsize}}} \right)dz} } = {2\left( {\frac{{{z^{ \frac{3}{2}\normalsize}}}}{{\frac{3}{2}}} – {C_1}\frac{{{z^{ \frac{1}{2}\normalsize}}}}{{\frac{1}{2}}}} \right) } \\ = {\frac{4}{3}{z^{ \frac{3}{2}\normalsize}} – 4{C_1}{z^{ \frac{1}{2}\normalsize}} } = {\frac{4}{3}\sqrt {{{\left( {\sqrt y + {C_1}} \right)}^3}} }-{ 4{C_1}\sqrt {\sqrt y + {C_1}} .} ∫ y + C 1 d y = ∫ z 2 ( z – C 1 ) d z = 2 ∫ ( z z – z C 1 ) d z = 2 ∫ ( z 2 1 – C 1 z – 2 1 ) d z = 2 ( 2 3 z 2 3 – C 1 2 1 z 2 1 ) = 3 4 z 2 3 –4 C 1 z 2 1 = 3 4 ( y + C 1 ) 3 − 4 C 1 y + C 1 .
در نهایت، معادله جبری زیر بهدست میآید:
4 3 ( y + C 1 ) 3 − 4 C 1 y + C 1 = C 2 ± x , {\frac{4}{3}\sqrt {{{\left( {\sqrt y + {C_1}} \right)}^3}} }-{ 4{C_1}\sqrt {\sqrt y + {C_1}} }={ {C_2} \pm x,} 3 4 ( y + C 1 ) 3 − 4 C 1 y + C 1 = C 2 ± x ,
معادله اخیر، جواب عمومی معادله دیفرانسیل است که در آن، C 1 C_1 C 1 C 2 C_2 C 2
نمونه سوال معادلات دیفرانسیل ۳۰
مسئله مقدار اولیه زیر را حل کنید.
y ′ ′ ′ − 4 y ′ ′ = 4 t + 3 u 6 ( t ) e 30 − 5 t , y ( 0 ) = − 3 y ′ ( 0 ) = 1 y ′ ′ ( 0 ) = 4 y''' - 4y'' = 4t + 3{u_6}\left( t \right){{\bf{e}}^{30 - 5t}},\hspace{0.25in}y\left( 0 \right) = - 3\,\,\,y'\left( 0 \right) = 1\,\,\,\,\,y''\left( 0 \right) = 4 y ′′′ − 4 y ′′ = 4 t + 3 u 6 ( t ) e 30 − 5 t , y ( 0 ) = − 3 y ′ ( 0 ) = 1 y ′′ ( 0 ) = 4
حل سوال ۳۰: ابتدا باید بررسی کنیم جابهجایی زمانی تابع پله u ( t ) u(t) u ( t )
y ′ ′ ′ − 4 y ′ ′ = 4 t + 3 u 6 ( t ) e − 5 ( t − 6 ) y''' - 4y'' = 4t + 3{u_6}\left( t \right){{\bf{e}}^{ - 5\left( {t - 6} \right)}} y ′′′ − 4 y ′′ = 4 t + 3 u 6 ( t ) e − 5 ( t − 6 )
میبینیم که جابهجایی e − 5 t {{\bf{e}}^{ - 5t}} e − 5 t
L { y ′ ′ ′ } = s 3 Y ( s ) − s 2 y ( 0 ) − s y ′ ( 0 ) − y ′ ′ ( 0 ) \mathcal{L}\left\{ {y'''} \right\} = {s^3}Y\left( s \right) - {s^2}y\left( 0 \right) - sy'\left( 0 \right) - y''\left( 0 \right) L { y ′′′ } = s 3 Y ( s ) − s 2 y ( 0 ) − s y ′ ( 0 ) − y ′′ ( 0 )
بنابراین، داریم:
s 3 Y ( s ) − s 2 y ( 0 ) − s y ′ ( 0 ) − y ′ ′ ( 0 ) − 4 ( s 2 Y ( s ) − s y ( 0 ) − y ′ ( 0 ) ) = 4 s 2 + 3 e − 6 s s + 5 ( s 3 − 4 s 2 ) Y ( s ) + 3 s 2 − 13 s = 4 s 2 + 3 e − 6 s s + 5 ( s 3 − 4 s 2 ) Y ( s ) = 4 s 2 − 3 s 2 + 13 s + 3 e − 6 s s + 5 ( s 3 − 4 s 2 ) Y ( s ) = 4 − 3 s 4 + 13 s 3 s 2 + 3 e − 6 s s + 5 Y ( s ) = 4 − 3 s 4 + 13 s 3 s 4 ( s − 4 ) + 3 e − 6 s s 2 ( s − 4 ) ( s + 5 ) Y ( s ) = F ( s ) + 3 e − 6 s G ( s ) \begin{align*}{s^3}Y\left( s \right) - {s^2}y\left( 0 \right) - sy'\left( 0 \right) - y''\left( 0 \right) - 4\left( {{s^2}Y\left( s \right) - sy\left( 0 \right) - y'\left( 0 \right)} \right) & = \frac{4}{{{s^2}}} + \frac{{3{{\bf{e}}^{ - 6s}}}}{{s + 5}}\\ \hspace{0.25in}\hspace{0.25in}\left( {{s^3} - 4{s^2}} \right)Y\left( s \right) + 3{s^2} - 13s & = \frac{4}{{{s^2}}} + \frac{{3{{\bf{e}}^{ - 6s}}}}{{s + 5}}\\ \hspace{0.25in}\hspace{0.25in}\left( {{s^3} - 4{s^2}} \right)Y\left( s \right) & = \frac{4}{{{s^2}}} - 3{s^2} + 13s + \frac{{3{{\bf{e}}^{ - 6s}}}}{{s + 5}}\\ \hspace{0.25in}\hspace{0.25in}\left( {{s^3} - 4{s^2}} \right)Y\left( s \right) & = \frac{{4 - 3{s^4} + 13{s^3}}}{{{s^2}}} + \frac{{3{{\bf{e}}^{ - 6s}}}}{{s + 5}}\\ \hspace{0.25in}\hspace{0.25in}\hspace{0.25in}\hspace{0.25in}\,\,\,\,\,\,\,\,Y\left( s \right) & = \frac{{4 - 3{s^4} + 13{s^3}}}{{{s^4}\left( {s - 4} \right)}} + \frac{{3{{\bf{e}}^{ - 6s}}}}{{{s^2}\left( {s - 4} \right)\left( {s + 5} \right)}}\\ \hspace{0.25in}\hspace{0.25in}\,\,\,\,\,\,\,\,\,\,\,Y\left( s \right) & = F\left( s \right) + 3{{\bf{e}}^{ - 6s}}G\left( s \right)\end{align*} s 3 Y ( s ) − s 2 y ( 0 ) − s y ′ ( 0 ) − y ′′ ( 0 ) − 4 ( s 2 Y ( s ) − sy ( 0 ) − y ′ ( 0 ) ) ( s 3 − 4 s 2 ) Y ( s ) + 3 s 2 − 13 s ( s 3 − 4 s 2 ) Y ( s ) ( s 3 − 4 s 2 ) Y ( s ) Y ( s ) Y ( s ) = s 2 4 + s + 5 3 e − 6 s = s 2 4 + s + 5 3 e − 6 s = s 2 4 − 3 s 2 + 13 s + s + 5 3 e − 6 s = s 2 4 − 3 s 4 + 13 s 3 + s + 5 3 e − 6 s = s 4 ( s − 4 ) 4 − 3 s 4 + 13 s 3 + s 2 ( s − 4 ) ( s + 5 ) 3 e − 6 s = F ( s ) + 3 e − 6 s G ( s )
اکنون تبدیل لاپلاس جواب مورد نظر را در اختیار داریم. برای بهدست آوردن جواب، باید F ( s ) F(s) F ( s ) G ( s ) G(s) G ( s )
F ( s ) = 4 − 3 s 4 + 13 s 3 s 4 ( s − 4 ) = 17 64 s − 4 − 209 64 s − 1 16 s 2 − 1 4 ( 2 ! 2 ! ) s 3 − 1 ( 3 ! 3 ! ) s 4 f ( t ) = 17 64 e 4 t − 209 64 − 1 16 t − 1 8 t 2 − 1 6 t 3 \begin{align*}F\left( s \right) & = \frac{{4 - 3{s^4} + 13{s^3}}}{{{s^4}\left( {s - 4} \right)}} = \frac{{\frac{{17}}{{64}}}}{{s - 4}} - \frac{{\frac{{209}}{{64}}}}{s} - \frac{{\frac{1}{{16}}}}{{{s^2}}} - \frac{{\frac{1}{4}\left( {\frac{{2!}}{{2!}}} \right)}}{{{s^3}}} - \frac{{1\left( {\frac{{3!}}{{3!}}} \right)}}{{{s^4}}}\\ f\left( t \right) & = \frac{{17}}{{64}}{{\bf{e}}^{4t}} - \frac{{209}}{{64}} - \frac{1}{{16}}t - \frac{1}{8}{t^2} - \frac{1}{6}{t^3}\end{align*} F ( s ) f ( t ) = s 4 ( s − 4 ) 4 − 3 s 4 + 13 s 3 = s − 4 64 17 − s 64 209 − s 2 16 1 − s 3 4 1 ( 2 ! 2 ! ) − s 4 1 ( 3 ! 3 ! ) = 64 17 e 4 t − 64 209 − 16 1 t − 8 1 t 2 − 6 1 t 3
G ( s ) = 1 s 2 ( s − 4 ) ( s + 5 ) = 1 144 s − 4 − 1 225 s + 5 − 1 400 s − 1 20 s 2 g ( t ) = 1 144 e 4 t − 1 225 e − 5 t − 1 400 − 1 20 t \begin{align*}G\left( s \right) & = \frac{1}{{{s^2}\left( {s - 4} \right)\left( {s + 5} \right)}} = \frac{{\frac{1}{{144}}}}{{s - 4}} - \frac{{\frac{1}{{225}}}}{{s + 5}} - \frac{{\frac{1}{{400}}}}{s} - \frac{{\frac{1}{{20}}}}{{{s^2}}}\\ g\left( t \right) & = \frac{1}{{144}}{{\bf{e}}^{4t}} - \frac{1}{{225}}{{\bf{e}}^{ - 5t}} - \frac{1}{{400}} - \frac{1}{{20}}t\end{align*} G ( s ) g ( t ) = s 2 ( s − 4 ) ( s + 5 ) 1 = s − 4 144 1 − s + 5 225 1 − s 400 1 − s 2 20 1 = 144 1 e 4 t − 225 1 e − 5 t − 400 1 − 20 1 t
اکنون میتوانیم جواب معادله دیفرانسیل را بهصورت زیر بنویسیم که در آن، f ( t ) f(t) f ( t ) g ( t ) g(t) g ( t )
Y ( s ) = F ( s ) + 3 e − 6 s G ( s ) ⇒ y ( t ) = f ( t ) + 3 u 6 ( t ) g ( t − 6 ) Y\left( s \right) = F\left( s \right) + 3{{\bf{e}}^{ - 6s}}G\left( s \right)\hspace{0.25in}\hspace{0.25in} \Rightarrow \hspace{0.25in}\hspace{0.25in}y\left( t \right) = f\left( t \right) + 3{u_6}\left( t \right)g\left( {t - 6} \right) Y ( s ) = F ( s ) + 3 e − 6 s G ( s ) ⇒ y ( t ) = f ( t ) + 3 u 6 ( t ) g ( t − 6 )
نمونه سوال معادلات دیفرانسیل ۳۱
معادله دیفرانسیل y y ′ ′ + ( y ’ ) 2 = 2 x + 1 yy^{\prime\prime} + {\left( {y’} \right)^2} =2x + 1 y y ′′ + ( y ’ ) 2 = 2 x + 1
حل سوال ۳۱: با در نظر گرفتن z = y y ’ z = yy’ z = yy ’
( y y ’ ) ′ = 2 x + 1 , ⇒ z ’ = 2 x + 1. {{\left( {yy’} \right)^\prime } = 2x + 1,\;\; }\Rightarrow{ z’ = 2x + 1.} ( yy ’ ) ′ = 2 x + 1 , ⇒ z ’ = 2 x + 1.
معادله اخیر را میتوان بهسادگی و با استفاده از جداسازی متغیرها حل کرد:
d z d x = 2 x + 1 , ⇒ d z = ( 2 x + 1 ) d x , ⇒ ∫ d z = ∫ ( 2 x + 1 ) d x , ⇒ z = x 2 + x + C 1 . {\frac{{dz}}{{dx}} = 2x + 1,\;\;}\Rightarrow {dz = \left( {2x + 1} \right)dx,\;\;}\\ \Rightarrow {\int {dz} = \int {\left( {2x + 1} \right)dx} ,\;\;}\Rightarrow {z = {x^2} + x + {C_1}.} d x d z = 2 x + 1 , ⇒ d z = ( 2 x + 1 ) d x , ⇒ ∫ d z = ∫ ( 2 x + 1 ) d x , ⇒ z = x 2 + x + C 1 .
با یادآوری تغییر متغیری که در نظر گرفتیم، تابع y ( x ) y(x) y ( x )
y y ’ = x 2 + x + C 1 , ⇒ ∫ y d y = ∫ ( x 2 + x + C 1 ) d x , ⇒ y 2 2 = x 3 3 + x 2 2 + C 1 x + C 2 , ⇒ 3 y 2 = 2 x 3 + 3 x 2 + C 1 x + C 2 , {yy’ = {x^2} + x + {C_1},\;\;}\\ \Rightarrow {{\int {ydy} }={ \int {\left( {{x^2} + x + {C_1}} \right)dx} ,\;\;}}\\\Rightarrow {{\frac{{{y^2}}}{2} = \frac{{{x^3}}}{3} + \frac{{{x^2}}}{2} }+{ {C_1}x + {C_2},\;\;}}\\ \Rightarrow {{3{y^2} = 2{x^3} + 3{x^2} }+{ {C_1}x + {C_2},}} yy ’ = x 2 + x + C 1 , ⇒ ∫ y d y = ∫ ( x 2 + x + C 1 ) d x , ⇒ 2 y 2 = 3 x 3 + 2 x 2 + C 1 x + C 2 , ⇒ 3 y 2 = 2 x 3 + 3 x 2 + C 1 x + C 2 ,
که در آن، C 1 C_1 C 1 C 2 C_2 C 2
نمونه سوال معادلات دیفرانسیل ۳۲
دستگاه معادلات دیفرانسیل زیر را حل کنید.
x ’ 1 = 2 x 1 + 3 x 2 , x ’ 2 = 4 x 1 – 2 x 2 . {{x’_1} = 2{x_1} + 3{x_2},\;\;\;}\kern-0.3pt{{x’_2} = 4{x_1} – 2{x_2}.} x ’ 1 = 2 x 1 + 3 x 2 , x ’ 2 = 4 x 1 –2 x 2 .
حل سوال ۳۲: ابتدا، از معادله نخست مشتق میگیریم، سپس x ’ 2 {x’_2} x ’ 2
x 1 ′ ′ = 2 x ’ 1 + 3 x ’ 2 , ⇒ x 1 ′ ′ = 2 x ’ 1 + 3 ( 4 x 1 – 2 x 2 ) , ⇒ x 1 ′ ′ = 2 x ’ 1 + 12 x 1 – 6 x 2 . {{x^{\prime\prime}_1} = 2{x’_1} + 3{x’_2},\;\;}\Rightarrow {{x^{\prime\prime}_1} = 2{x’_1} + 3\left( {4{x_1} – 2{x_2}} \right),\;\;}\\ \Rightarrow {{x^{\prime\prime}_1} = 2{x’_1} + 12{x_1} – 6{x_2}.} x 1 ′′ = 2 x ’ 1 + 3 x ’ 2 , ⇒ x 1 ′′ = 2 x ’ 1 + 3 ( 4 x 1 –2 x 2 ) , ⇒ x 1 ′′ = 2 x ’ 1 + 12 x 1 –6 x 2 .
مقدار 3 x 2 3{x_2} 3 x 2
3 x 2 = x ’ 1 – 2 x 1 . 3{x_2} = {x’_1} – 2{x_1}. 3 x 2 = x ’ 1 –2 x 1 .
بنابراین، داریم:
$$\require{cancel}<br />
{{{x^{\prime\prime}_1} = 2{x’_1} + 12{x_1} }-{ 2\left( {{x’_1} – 2{x_1}} \right),\;\;}}\\<br />
\Rightarrow<br />
{{{x^{\prime\prime}_1} = \cancel{2{x’_1}} + 12{x_1} }-{ \cancel{2{x’_1}} + 4{x_1},\;\;}}\\<br />
\Rightarrow<br />
{{x^{\prime\prime}_1} – 16{x_1} = 0.}$$
ریشههای معادله مشخصه بهصورت زیر محاسبه میشوند:
λ 2 – 16 = 0 , ⇒ λ 1 , 2 = ± 4. {{\lambda ^2} – 16 = 0,\;\; }\Rightarrow{ {\lambda _{1,2}} = \pm 4.} λ 2 –16 = 0 , ⇒ λ 1 , 2 = ± 4.
در نتیجه، حل معادله مرتبه دوم متغیر x 1 x_1 x 1
x 1 ( t ) = C 1 e 4 t + C 2 e – 4 t , {{x_1}\left( t \right) }={ {C_1}{e^{4t}} + {C_2}{e^{ – 4t}},} x 1 ( t ) = C 1 e 4 t + C 2 e –4 t ,
که در آن، C 1 C_1 C 1 C 2 C_2 C 2
اکنون باید x ’ 1 {x’_1} x ’ 1 x 2 x_2 x 2
x ’ 1 ( t ) = 4 C 1 e 4 t – 4 C 2 e – 4 t , ⇒ 4 C 1 e 4 t – 4 C 2 e – 4 t = 2 C 1 e 4 t + 2 C 2 e – 4 t + 3 x 2 , ⇒ 3 x 2 = 2 C 1 e 4 t – 6 C 2 e – 4 t , ⇒ x 2 = 2 3 C 1 e 4 t – 2 C 2 e – 4 t . {{x’_1}\left( t \right) = 4{C_1}{e^{4t}} – 4{C_2}{e^{ – 4t}},\;\;}\\ \Rightarrow {4{C_1}{e^{4t}} – 4{C_2}{e^{ – 4t}} }={ 2{C_1}{e^{4t}} + 2{C_2}{e^{ – 4t}} + 3{x_2},\;\;}\\ \Rightarrow {3{x_2} = 2{C_1}{e^{4t}} – 6{C_2}{e^{ – 4t}},\;\;}\\ \Rightarrow {{x_2} = \frac{2}{3}{C_1}{e^{4t}} – 2{C_2}{e^{ – 4t}}.} x ’ 1 ( t ) = 4 C 1 e 4 t –4 C 2 e –4 t , ⇒ 4 C 1 e 4 t –4 C 2 e –4 t = 2 C 1 e 4 t + 2 C 2 e –4 t + 3 x 2 , ⇒ 3 x 2 = 2 C 1 e 4 t –6 C 2 e –4 t , ⇒ x 2 = 3 2 C 1 e 4 t –2 C 2 e –4 t .
برای آنکه ضرایب را از حالت کسری در بیاوریم، بهجای C 1 C_1 C 1 3 C 1 3C_1 3 C 1
{ x 1 ( t ) = 3 C 1 e 4 t + C 2 e – 4 t x 2 ( t ) = 2 C 1 e 4 t – 2 C 2 e – 4 t . \left\{ \begin{array}{l} {x_1}\left( t \right) = 3{C_1}{e^{4t}} + {C_2}{e^{ – 4t}}\\ {x_2}\left( t \right) = 2{C_1}{e^{4t}} – 2{C_2}{e^{ – 4t}} \end{array} \right.. { x 1 ( t ) = 3 C 1 e 4 t + C 2 e –4 t x 2 ( t ) = 2 C 1 e 4 t –2 C 2 e –4 t .
نمونه سوال معادلات دیفرانسیل ۳۳
جواب دستگاه معادلات زیر را با روش تغییر ثوابت بهدست آورید.
d x d t = 2 x – y + e 2 t , d y d t = 6 x – 3 y + e t + 1. {\frac{{dx}}{{dt}} = 2x – y + {e^{2t}},\;\;}\kern-0.3pt {{\frac{{dy}}{{dt}} = 6x – 3y }+{ {e^t} + 1.}} d t d x = 2 x – y + e 2 t , d t d y = 6 x –3 y + e t + 1.
حل: این دستگاه معادلات ناهمگن است. قبل از هر چیز، جواب عمومی دستگاه همگن را محاسبه میکنیم. مقادیر ویژه ماتریس A A A
$$ {\det \left( {A – \lambda I} \right) = \left| {\begin{array}{*{20}{c}}<br />
2&{ – 1}\\<br />
6&{ – 3}<br />
\end{array}} \right| = 0,\;\;}\Rightarrow<br />
{\left( {2 – \lambda } \right)\left( { – 3 – \lambda } \right) + 6 = 0,\;\;} \\ \Rightarrow<br />
{\left( {\lambda – 2} \right)\left( {\lambda + 3} \right) + 6 = 0,\;\;}\Rightarrow<br />
{{\lambda ^2} – 2\lambda + 3\lambda – \cancel{6} + \cancel{6} = 0,\;\;} \\ \Rightarrow<br />
{{\lambda ^2} + \lambda = 0,\;\;} \Rightarrow<br />
{\lambda \left( {\lambda + 1} \right) = 0,\;\;}\Rightarrow<br />
{{\lambda _1} = 0,\;{\lambda _2} = – 1.} $$
بردار ویژه V 1 = ( V 11 , V 21 ) T {\mathbf{V}_1} = {\left( {{V_{11}},{V_{21}}} \right)^T} V 1 = ( V 11 , V 21 ) T λ 1 = 0 {\lambda _1} = 0 λ 1 = 0
$$ {\left( {A – {\lambda _1}I} \right){\mathbf{V}_1} = \mathbf{0},\;\;}\Rightarrow<br />
{\left[ {\begin{array}{*{20}{c}}<br />
2&{ – 1}\\<br />
6&{ – 3}<br />
\end{array}} \right]\left[ {\begin{array}{*{20}{c}}<br />
{{V_{11}}}\\<br />
{{V_{21}}}<br />
\end{array}} \right] = \mathbf{0},\;\;} \\ \Rightarrow<br />
{2{V_{11}} – {V_{21}} = 0,\;\;}\Rightarrow<br />
{{V_{11}} = t,}\;\;<br />
{{V_{21}} = 2{V_{11}} = 2t,\;\;} \\ \Rightarrow<br />
{{\mathbf{V}_1} = \left[ {\begin{array}{*{20}{c}}<br />
{{V_{11}}}\\<br />
{{V_{21}}}<br />
\end{array}} \right] }<br />
= {\left[ {\begin{array}{*{20}{c}}<br />
t\\<br />
{2t}<br />
\end{array}} \right] }<br />
= {t\left[ {\begin{array}{*{20}{c}}<br />
1\\<br />
2<br />
\end{array}} \right] }<br />
\sim {\left[ {\begin{array}{*{20}{c}}<br />
1\\<br />
2<br />
\end{array}} \right].} $$
به طور مشابه، بردار ویژه V 2 = ( V 12 , V 22 ) T {\mathbf{V}_2} = {\left( {{V_{12}},{V_{22}}} \right)^T} V 2 = ( V 12 , V 22 ) T λ 2 = − 1 {\lambda _2} = -1 λ 2 = − 1
$$ {\left( {A – {\lambda _2}I} \right){\mathbf{V}_2} = \mathbf{0},\;\;}\Rightarrow<br />
{\left[ {\begin{array}{*{20}{c}}<br />
3&{ – 1}\\<br />
6&{ – 2}<br />
\end{array}} \right]\left[ {\begin{array}{*{20}{c}}<br />
{{V_{12}}}\\<br />
{{V_{22}}}<br />
\end{array}} \right] = \mathbf{0},\;\;} \\ \Rightarrow<br />
{3{V_{12}} – {V_{22}} = 0,\;\;}\Rightarrow<br />
{{V_{12}} = t,}\;\;<br />
{{V_{22}} = 3{V_{12}} = 3t,\;\;} \\ \Rightarrow<br />
{{\mathbf{V}_2} = \left[ {\begin{array}{*{20}{c}}<br />
{{V_{12}}}\\<br />
{{V_{22}}}<br />
\end{array}} \right] }<br />
= {\left[ {\begin{array}{*{20}{c}}<br />
t\\<br />
{3t}<br />
\end{array}} \right] }<br />
= {t\left[ {\begin{array}{*{20}{c}}<br />
1\\<br />
3<br />
\end{array}} \right] }<br />
\sim {\left[ {\begin{array}{*{20}{c}}<br />
1\\<br />
3<br />
\end{array}} \right].} $$
بنابراین، جواب عمومی دستگاه معادلات همگن برابر است با
$$ {{\mathbf{X}_0}\left( t \right) }={ \left[ {\begin{array}{*{20}{c}}<br />
{{x_0}\left( t \right)}\\<br />
{{y_0}\left( t \right)}<br />
\end{array}} \right] }<br />
= {{C_1}\left[ {\begin{array}{*{20}{c}}<br />
1\\<br />
2<br />
\end{array}} \right] + {C_2}{e^{ – t}}\left[ {\begin{array}{*{20}{c}}<br />
1\\<br />
3<br />
\end{array}} \right]} $$
که در آن، C 1 C_1 C 1 C 2 C_2 C 2
اکنون دستگاه ناهمگن اصلی را در نظر گرفته و جواب آن را با استفاده از تغییر پارامترها به دست میآوریم. بدین منظور C 1 C_1 C 1 C 2 C_2 C 2 C 1 ( t ) C_1(t) C 1 ( t ) C 2 ( t ) C_2(t) C 2 ( t )
$$ {\mathbf{X}\left( t \right) }={ {C_1}\left( t \right)\left[ {\begin{array}{*{20}{c}}<br />
1\\<br />
2<br />
\end{array}} \right] }+{ {C_2}\left( t \right){e^{ – t}}\left[ {\begin{array}{*{20}{c}}<br />
1\\<br />
3<br />
\end{array}} \right]} $$
یا
{ x ( t ) = C 1 ( t ) + C 2 ( t ) e – t y ( t ) = 2 C 1 ( t ) + 3 C 2 ( t ) e – t . \left\{ \begin{array}{l} x\left( t \right) = {C_1}\left( t \right) + {C_2}\left( t \right){e^{ – t}}\\ y\left( t \right) = 2{C_1}\left( t \right) + 3{C_2}\left( t \right){e^{ – t}} \end{array} \right.. { x ( t ) = C 1 ( t ) + C 2 ( t ) e – t y ( t ) = 2 C 1 ( t ) + 3 C 2 ( t ) e – t .
مشتق این توابع برابر است با:
{ x ’ ( t ) = C ’ 1 + C ’ 2 e – t – C 2 e – t y ’ ( t ) = 2 C ’ 1 + 3 C ’ 2 e – t – 3 C 2 e – t . \left\{ \begin{array}{l} {x’\left( t \right) }={ {C’_1} + {C’_2}{e^{ – t}} – {C_2}{e^{ – t}} }\\ {y’\left( t \right) }={ 2{C’_1} + 3{C’_2}{e^{ – t}} – 3{C_2}{e^{ – t}} } \end{array} \right.. { x ’ ( t ) = C ’ 1 + C ’ 2 e – t – C 2 e – t y ’ ( t ) = 2 C ’ 1 + 3 C ’ 2 e – t –3 C 2 e – t .
در ادامه، عبارات بالا را در دستگاه ناهمگن قرار میدهیم:
$$ {\left\{ \begin{array}{l}<br />
{{C’_1} + {C’_2}{e^{ – t}} – \cancel{{C_2}{e^{ – t}}} }={ \cancel{2{C_1}} + \cancel{2{C_2}{e^{ – t}}} }-{ \cancel{2{C_1}} – \cancel{3{C_2}{e^{ – t}}} }+{ {e^{2t}} }\\<br />
{2{C’_1} + 3{C’_2}{e^{ – t}} – \cancel{3{C_2}{e^{ – t}}} }={ \cancel{6{C_1}} + \cancel{6{C_2}{e^{ – t}}} }-{ \cancel{6{C_1}} – \cancel{9{C_2}{e^{ – t}}} }+{ {e^t} + 1}<br />
\end{array} \right.,\;\;} \\ \Rightarrow<br />
{\left\{ {\begin{array}{*{20}{l}}<br />
{{C’_1} + {C’_2}{e^{ – t}} = {e^{2t}}}\\<br />
{2{C’_1} + 3{C’_2}{e^{ – t}} = {e^t} + 1}<br />
\end{array}} \right.} $$
اکنون دو معادله جبری برای C ’ 1 {C’_1} C ’ 1 C ’ 2 {C’_2} C ’ 2 C 1 ( t ) C_1(t) C 1 ( t ) C 2 ( t ) C_2(t) C 2 ( t )
$$ {\Delta = \left| {\begin{array}{*{20}{c}}<br />
1&{{e^{ – t}}}\\<br />
2&{3{e^{ – 2t}}}<br />
\end{array}} \right| }<br />
= {3{e^{ – t}} – 2{e^{ – t}} = {e^{ – t}},} $$
$$ {{\Delta _1} = \left| {\begin{array}{*{20}{c}}<br />
{{e^{2t}}}&{{e^{ – t}}}\\<br />
{{e^t} + 1}&{3{e^{ – 2t}}}<br />
\end{array}} \right| }<br />
= {3{e^{2t}}{e^{ – t}} – {e^{ – t}}\left( {{e^t} + 1} \right) }<br />
= {3{e^t} – {e^{ – t}} – 1,} $$
$$ {{\Delta _2} = \left| {\begin{array}{*{20}{c}}<br />
1&{{e^{2t}}}\\<br />
2&{{e^t} + 1}<br />
\end{array}} \right| }<br />
= {{e^t} – 2{e^{2t}} + 1,} $$
⇒ C ’ 1 = Δ 1 Δ = 3 e t – e – t – 1 e – t = 3 e 2 t + e t – 1 , \Rightarrow{ {C’_1} = \frac{{{\Delta _1}}}{\Delta } }={ \frac{{3{e^t} – {e^{ – t}} – 1}}{{{e^{ – t}}}} } = {3{e^{2t}} + {e^t} – 1,} ⇒ C ’ 1 = Δ Δ 1 = e – t 3 e t – e – t –1 = 3 e 2 t + e t –1 ,
⇒ C ’ 2 = Δ 2 Δ = e t – 2 e 2 t + 1 e – t = e 2 t – 2 e 3 t + e t . \Rightarrow{ {C’_2} = \frac{{{\Delta _2}}}{\Delta } }={ \frac{{{e^t} – 2{e^{2t}} + 1}}{{{e^{ – t}}}} } = {{e^{2t}} – 2{e^{3t}} + {e^t}.} ⇒ C ’ 2 = Δ Δ 2 = e – t e t –2 e 2 t + 1 = e 2 t –2 e 3 t + e t .
با انتگرالگیری، عبارات مورد نظر محاسبه میشود:
C 1 ( t ) = ∫ ( 3 e 2 t + e t – 1 ) d t = 3 2 e 2 t + e t – t + A 1 , {{C_1}\left( t \right) }={ \int {\left( {3{e^{2t}} + {e^t} – 1} \right)dt} } = {\frac{3}{2}{e^{2t}} + {e^t} – t + {A_1},} C 1 ( t ) = ∫ ( 3 e 2 t + e t –1 ) d t = 2 3 e 2 t + e t – t + A 1 ,
C 2 ( t ) = ∫ ( e 2 t – 2 e 3 t + e t ) d t = 1 2 e 2 t – 2 3 e 3 t + e t + A 2 . {{C_2}\left( t \right) }={ \int {\left( {{e^{2t}} – 2{e^{3t}} + {e^t}} \right)dt} } = {\frac{1}{2}{e^{2t}} – \frac{2}{3}{e^{3t}} + {e^t} + {A_2}.} C 2 ( t ) = ∫ ( e 2 t –2 e 3 t + e t ) d t = 2 1 e 2 t – 3 2 e 3 t + e t + A 2 .
در نتیجه، توابع x ( t ) x(t) x ( t ) y ( t ) y(t) y ( t )
x ( t ) = C 1 ( t ) + C 2 ( t ) e – t = ( 3 2 e 2 t + e t – t + A 1 ) + ( 1 2 e 2 t – 2 3 e 3 t + e t + A 2 ) e – t = A 1 + A 2 e – t + 5 9 e 2 t + 3 2 e t – t + 1 {x\left( t \right) = {C_1}\left( t \right) + {C_2}\left( t \right){e^{ – t}} } \\ = {{\left( {\frac{3}{2}{e^{2t}} + {e^t} – t + {A_1}} \right) } + {\left( {\frac{1}{2}{e^{2t}} – \frac{2}{3}{e^{3t}} }\right.}+{\left.{ {e^t} + {A_2}} \right){e^{ – t}} }} \\ = {{A_1} + {A_2}{e^{ – t}} + \frac{5}{9}{e^{2t}} } + {\frac{3}{2}{e^t} – t + 1} x ( t ) = C 1 ( t ) + C 2 ( t ) e – t = ( 2 3 e 2 t + e t – t + A 1 ) + ( 2 1 e 2 t – 3 2 e 3 t + e t + A 2 ) e – t = A 1 + A 2 e – t + 9 5 e 2 t + 2 3 e t – t + 1
و
y ( t ) = 2 C 1 ( t ) + 3 C 2 ( t ) e – t = 2 ( 3 2 e 2 t + e t – t + A 1 ) + 3 ( 1 2 e 2 t – 2 3 e 3 t + e t + A 2 ) e – t = 2 A 1 + 3 A 2 e – t + e 2 t + 7 2 e t – 2 t + 3. {y\left( t \right) = 2{C_1}\left( t \right) + 3{C_2}\left( t \right){e^{ – t}} } \\ = {{2\left( {\frac{3}{2}{e^{2t}} + {e^t} – t + {A_1}} \right) } + {3\left( {\frac{1}{2}{e^{2t}} – \frac{2}{3}{e^{3t}} }\right.}+{\left.{ {e^t} + {A_2}} \right){e^{ – t}} }} \\ = {2{A_1} + 3{A_2}{e^{ – t}} + {e^{2t}} } + {\frac{7}{2}{e^t} – 2t + 3.} y ( t ) = 2 C 1 ( t ) + 3 C 2 ( t ) e – t = 2 ( 2 3 e 2 t + e t – t + A 1 ) + 3 ( 2 1 e 2 t – 3 2 e 3 t + e t + A 2 ) e – t = 2 A 1 + 3 A 2 e – t + e 2 t + 2 7 e t –2 t + 3.
جواب نهایی را میتوان به صورت زیر نوشت:
$$ {\mathbf{X}\left( t \right) = \left[ {\begin{array}{*{20}{c}}<br />
{x\left( t \right)}\\<br />
{y\left( t \right)}<br />
\end{array}} \right] }<br />
= {{A_1}\left[ {\begin{array}{*{20}{c}}<br />
1\\<br />
2<br />
\end{array}} \right] }+{ {A_2}{e^{ – t}}\left[ {\begin{array}{*{20}{c}}<br />
1\\<br />
3<br />
\end{array}} \right] }<br />
+ {\left[ {\begin{array}{*{20}{c}}<br />
{\frac{5}{9}{e^{2t}} + \frac{3}{2}{e^t} – t + 1}\\<br />
{{e^{2t}} + \frac{7}{2}{e^t} – 2t + 3}<br />
\end{array}} \right].} $$
نمونه سوال معادلات دیفرانسیل ۳۴
جواب معادله زیر را بهدست آورید.
y ′ ′ ′ − 4 y ′ ′ = 4 t + 3 u 6 ( t ) e 30 − 5 t , y ( 0 ) = − 3 y ′ ( 0 ) = 1 y ′ ′ ( 0 ) = 4 y''' - 4y'' = 4t + 3{u_6}\left( t \right){{\bf{e}}^{30 - 5t}},\hspace{0.25in}y\left( 0 \right) = - 3\,\,\,y'\left( 0 \right) = 1\,\,\,\,\,y''\left( 0 \right) = 4 y ′′′ − 4 y ′′ = 4 t + 3 u 6 ( t ) e 30 − 5 t , y ( 0 ) = − 3 y ′ ( 0 ) = 1 y ′′ ( 0 ) = 4
حل سوال ۳۴: ابتدا باید بررسی کنیم جابهجایی زمانی تابع پله u ( t ) u(t) u ( t )
y ′ ′ ′ − 4 y ′ ′ = 4 t + 3 u 6 ( t ) e − 5 ( t − 6 ) y''' - 4y'' = 4t + 3{u_6}\left( t \right){{\bf{e}}^{ - 5\left( {t - 6} \right)}} y ′′′ − 4 y ′′ = 4 t + 3 u 6 ( t ) e − 5 ( t − 6 )
میبینیم که جابهجایی e − 5 t {{\bf{e}}^{ - 5t}} e − 5 t
L { y ′ ′ ′ } = s 3 Y ( s ) − s 2 y ( 0 ) − s y ′ ( 0 ) − y ′ ′ ( 0 ) \mathcal{L}\left\{ {y'''} \right\} = {s^3}Y\left( s \right) - {s^2}y\left( 0 \right) - sy'\left( 0 \right) - y''\left( 0 \right) L { y ′′′ } = s 3 Y ( s ) − s 2 y ( 0 ) − s y ′ ( 0 ) − y ′′ ( 0 )
بنابراین، داریم:
s 3 Y ( s ) − s 2 y ( 0 ) − s y ′ ( 0 ) − y ′ ′ ( 0 ) − 4 ( s 2 Y ( s ) − s y ( 0 ) − y ′ ( 0 ) ) = 4 s 2 + 3 e − 6 s s + 5 ( s 3 − 4 s 2 ) Y ( s ) + 3 s 2 − 13 s = 4 s 2 + 3 e − 6 s s + 5 ( s 3 − 4 s 2 ) Y ( s ) = 4 s 2 − 3 s 2 + 13 s + 3 e − 6 s s + 5 ( s 3 − 4 s 2 ) Y ( s ) = 4 − 3 s 4 + 13 s 3 s 2 + 3 e − 6 s s + 5 Y ( s ) = 4 − 3 s 4 + 13 s 3 s 4 ( s − 4 ) + 3 e − 6 s s 2 ( s − 4 ) ( s + 5 ) Y ( s ) = F ( s ) + 3 e − 6 s G ( s ) \begin{align*}{s^3}Y\left( s \right) - {s^2}y\left( 0 \right) - sy'\left( 0 \right) - y''\left( 0 \right) - 4\left( {{s^2}Y\left( s \right) - sy\left( 0 \right) - y'\left( 0 \right)} \right) & = \frac{4}{{{s^2}}} + \frac{{3{{\bf{e}}^{ - 6s}}}}{{s + 5}}\\ \hspace{0.25in}\hspace{0.25in}\left( {{s^3} - 4{s^2}} \right)Y\left( s \right) + 3{s^2} - 13s & = \frac{4}{{{s^2}}} + \frac{{3{{\bf{e}}^{ - 6s}}}}{{s + 5}}\\ \hspace{0.25in}\hspace{0.25in}\left( {{s^3} - 4{s^2}} \right)Y\left( s \right) & = \frac{4}{{{s^2}}} - 3{s^2} + 13s + \frac{{3{{\bf{e}}^{ - 6s}}}}{{s + 5}}\\ \hspace{0.25in}\hspace{0.25in}\left( {{s^3} - 4{s^2}} \right)Y\left( s \right) & = \frac{{4 - 3{s^4} + 13{s^3}}}{{{s^2}}} + \frac{{3{{\bf{e}}^{ - 6s}}}}{{s + 5}}\\ \hspace{0.25in}\hspace{0.25in}\hspace{0.25in}\hspace{0.25in}\,\,\,\,\,\,\,\,Y\left( s \right) & = \frac{{4 - 3{s^4} + 13{s^3}}}{{{s^4}\left( {s - 4} \right)}} + \frac{{3{{\bf{e}}^{ - 6s}}}}{{{s^2}\left( {s - 4} \right)\left( {s + 5} \right)}}\\ \hspace{0.25in}\hspace{0.25in}\,\,\,\,\,\,\,\,\,\,\,Y\left( s \right) & = F\left( s \right) + 3{{\bf{e}}^{ - 6s}}G\left( s \right)\end{align*} s 3 Y ( s ) − s 2 y ( 0 ) − s y ′ ( 0 ) − y ′′ ( 0 ) − 4 ( s 2 Y ( s ) − sy ( 0 ) − y ′ ( 0 ) ) ( s 3 − 4 s 2 ) Y ( s ) + 3 s 2 − 13 s ( s 3 − 4 s 2 ) Y ( s ) ( s 3 − 4 s 2 ) Y ( s ) Y ( s ) Y ( s ) = s 2 4 + s + 5 3 e − 6 s = s 2 4 + s + 5 3 e − 6 s = s 2 4 − 3 s 2 + 13 s + s + 5 3 e − 6 s = s 2 4 − 3 s 4 + 13 s 3 + s + 5 3 e − 6 s = s 4 ( s − 4 ) 4 − 3 s 4 + 13 s 3 + s 2 ( s − 4 ) ( s + 5 ) 3 e − 6 s = F ( s ) + 3 e − 6 s G ( s )
اکنون تبدیل لاپلاس جواب مورد نظر را در اختیار داریم. برای بهدست آوردن جواب، باید F ( s ) F(s) F ( s ) G ( s ) G(s) G ( s )
F ( s ) = 4 − 3 s 4 + 13 s 3 s 4 ( s − 4 ) = 17 64 s − 4 − 209 64 s − 1 16 s 2 − 1 4 ( 2 ! 2 ! ) s 3 − 1 ( 3 ! 3 ! ) s 4 f ( t ) = 17 64 e 4 t − 209 64 − 1 16 t − 1 8 t 2 − 1 6 t 3 \begin{align*}F\left( s \right) & = \frac{{4 - 3{s^4} + 13{s^3}}}{{{s^4}\left( {s - 4} \right)}} = \frac{{\frac{{17}}{{64}}}}{{s - 4}} - \frac{{\frac{{209}}{{64}}}}{s} - \frac{{\frac{1}{{16}}}}{{{s^2}}} - \frac{{\frac{1}{4}\left( {\frac{{2!}}{{2!}}} \right)}}{{{s^3}}} - \frac{{1\left( {\frac{{3!}}{{3!}}} \right)}}{{{s^4}}}\\ f\left( t \right) & = \frac{{17}}{{64}}{{\bf{e}}^{4t}} - \frac{{209}}{{64}} - \frac{1}{{16}}t - \frac{1}{8}{t^2} - \frac{1}{6}{t^3}\end{align*} F ( s ) f ( t ) = s 4 ( s − 4 ) 4 − 3 s 4 + 13 s 3 = s − 4 64 17 − s 64 209 − s 2 16 1 − s 3 4 1 ( 2 ! 2 ! ) − s 4 1 ( 3 ! 3 ! ) = 64 17 e 4 t − 64 209 − 16 1 t − 8 1 t 2 − 6 1 t 3
G ( s ) = 1 s 2 ( s − 4 ) ( s + 5 ) = 1 144 s − 4 − 1 225 s + 5 − 1 400 s − 1 20 s 2 g ( t ) = 1 144 e 4 t − 1 225 e − 5 t − 1 400 − 1 20 t \begin{align*}G\left( s \right) & = \frac{1}{{{s^2}\left( {s - 4} \right)\left( {s + 5} \right)}} = \frac{{\frac{1}{{144}}}}{{s - 4}} - \frac{{\frac{1}{{225}}}}{{s + 5}} - \frac{{\frac{1}{{400}}}}{s} - \frac{{\frac{1}{{20}}}}{{{s^2}}}\\ g\left( t \right) & = \frac{1}{{144}}{{\bf{e}}^{4t}} - \frac{1}{{225}}{{\bf{e}}^{ - 5t}} - \frac{1}{{400}} - \frac{1}{{20}}t\end{align*} G ( s ) g ( t ) = s 2 ( s − 4 ) ( s + 5 ) 1 = s − 4 144 1 − s + 5 225 1 − s 400 1 − s 2 20 1 = 144 1 e 4 t − 225 1 e − 5 t − 400 1 − 20 1 t
اکنون میتوانیم جواب معادله دیفرانسیل را بهصورت زیر بنویسیم که در آن، f ( t ) f(t) f ( t ) g ( t ) g(t) g ( t )
Y ( s ) = F ( s ) + 3 e − 6 s G ( s ) ⇒ y ( t ) = f ( t ) + 3 u 6 ( t ) g ( t − 6 ) Y\left( s \right) = F\left( s \right) + 3{{\bf{e}}^{ - 6s}}G\left( s \right)\hspace{0.25in}\hspace{0.25in} \Rightarrow \hspace{0.25in}\hspace{0.25in}y\left( t \right) = f\left( t \right) + 3{u_6}\left( t \right)g\left( {t - 6} \right) Y ( s ) = F ( s ) + 3 e − 6 s G ( s ) ⇒ y ( t ) = f ( t ) + 3 u 6 ( t ) g ( t − 6 )
نمونه سوال معادلات دیفرانسیل ۳۵
جواب عمومی معادله بسل زیر را محاسبه کنید.
x 2 y ′ ′ + 2 x y ’ + ( x 2 – 1 ) y = 0. {x^2}y^{\prime\prime} + 2xy’+ \left( {{x^2} – 1} \right)y= 0. x 2 y ′′ + 2 x y ’ + ( x 2 –1 ) y = 0.
حل سوال ۳۵: از تغییر متغیر استفاده میکنیم:
y = x 1 – 2 2 z = x – 1 2 z , ⇒ y ’ = – 1 2 x – 3 2 z + x – 1 2 z ’ , ⇒ y ′ ′ = 3 4 x – 5 2 z – 1 2 x – 3 2 z ’– 1 2 x – 3 2 z ’ + x – 1 2 z ′ ′ = 3 4 x – 5 2 z – x – 3 2 z ’ + x – 1 2 z ′ ′ . {y = {x^{ \frac{{1 – 2}}{2}\normalsize}}z = {x^{ – \frac{1}{2}\normalsize}}z,\;\;}\\ \Rightarrow { y’ = – \frac{1}{2}{x^{ – \frac{3}{2}\normalsize}}z + {x^{ – \frac{1}{2}\normalsize}}z’,\;\;}\\ \Rightarrow {y^{\prime\prime} = \frac{3}{4}{x^{ – \frac{5}{2}\normalsize}}z – \frac{1}{2}{x^{ – \frac{3}{2}\normalsize}}z’ – \frac{1}{2}{x^{ – \frac{3}{2}\normalsize}}z’ }+{ {x^{ – \frac{1}{2}\normalsize}}z^{\prime\prime} } \\ = {\frac{3}{4}{x^{ – \frac{5}{2}\normalsize}}z – {x^{ – \frac{3}{2}\normalsize}}z’ }+{ {x^{ – \frac{1}{2}\normalsize}}z^{\prime\prime}.} y = x 2 1–2 z = x – 2 1 z , ⇒ y ’ = – 2 1 x – 2 3 z + x – 2 1 z ’ , ⇒ y ′′ = 4 3 x – 2 5 z – 2 1 x – 2 3 z ’– 2 1 x – 2 3 z ’ + x – 2 1 z ′′ = 4 3 x – 2 5 z – x – 2 3 z ’ + x – 2 1 z ′′ .
با قرار دادن عبارت بالا در معادله، خواهیم داشت:
x 2 y ′ ′ + 2 x y ’ + ( x 2 – 1 ) y = 0 , ⇒ x 2 ( 3 4 x – 5 2 z – x – 3 2 z ’ + x – 1 2 z ′ ′ ) + 2 x ( – 1 2 x – 3 2 z + x – 1 2 z ’ ) + ( x 2 – 1 ) x – 1 2 z = 0 , ⇒ 3 4 x – 1 2 z – x – 1 2 z ’ + x 3 2 z ′ ′ – x – 1 2 z + 2 x 1 2 z ’ + x 3 2 z – x – 1 2 z = 0 , ⇒ x 3 2 z ′ ′ + x – 1 2 z ’ + ( – 5 4 x – 1 2 + x 3 2 ) z = 0 , ⇒ x 2 z ′ ′ + x z ’ + ( x 2 – 5 4 ) z = 0. {x^2}y^{\prime\prime} + 2xy’ + \left( {{x^2} – 1} \right)y = 0,\;\Rightarrow \\ {{x^2}\left( {\frac{3}{4}{x^{ – \frac{5}{2}\normalsize}}z – {x^{ – \frac{3}{2}\normalsize}}z’ }+{ {x^{ – \frac{1}{2}\normalsize}}z^{\prime\prime}} \right) } + {2x\left( { – \frac{1}{2}{x^{ – \frac{3}{2}\normalsize}}z }+{ {x^{ – \frac{1}{2}\normalsize}}z’} \right) } + {\left( {{x^2} – 1} \right){x^{ – \frac{1}{2}\normalsize}}z = 0,} \\ {\Rightarrow \color{blue}{\frac{3}{4}{x^{ – \frac{1}{2}\normalsize}}z} } – {\color{red}{{x^{ – \frac{1}{2}\normalsize}}z’} + {x^{ \frac{3}{2}\normalsize}}z^{\prime\prime} } – {\color{blue}{{x^{ – \frac{1}{2}\normalsize}}z} + \color{red}{2{x^{ \frac{1}{2}\normalsize}}z’} } + {\color{blue}{{x^{ \frac{3}{2}\normalsize}}z} – \color{blue}{{x^{ – \frac{1}{2}\normalsize}}z} = 0,} \\ \Rightarrow {{x^{ \frac{3}{2}\normalsize}}z^{\prime\prime} + \color{red}{{x^{ – \frac{1}{2}\normalsize}}z’} }+{\color{blue}{\left( { – \frac{5}{4}{x^{ – \frac{1}{2}\normalsize}} + {x^{ \frac{3}{2}\normalsize}}} \right)z} }={ 0}, \\ \Rightarrow {{x^2}z^{\prime\prime} + xz’ }+{ \left( {{x^2} – \frac{5}{4}} \right)z }={ 0.} x 2 y ′′ + 2 x y ’ + ( x 2 –1 ) y = 0 , ⇒ x 2 ( 4 3 x – 2 5 z – x – 2 3 z ’ + x – 2 1 z ′′ ) + 2 x ( – 2 1 x – 2 3 z + x – 2 1 z ’ ) + ( x 2 –1 ) x – 2 1 z = 0 , ⇒ 4 3 x – 2 1 z – x – 2 1 z ’ + x 2 3 z ′′ – x – 2 1 z + 2 x 2 1 z ’ + x 2 3 z – x – 2 1 z = 0 , ⇒ x 2 3 z ′′ + x – 2 1 z ’ + ( – 4 5 x – 2 1 + x 2 3 ) z = 0 , ⇒ x 2 z ′′ + x z ’ + ( x 2 – 4 5 ) z = 0.
در نتیجه، داریم:
n 2 = v 2 + 1 4 ( a – 1 ) 2 = 1 + 1 4 ( 2 – 1 ) 2 = 1 + 1 4 = 5 4 . {{n^2} = {v^2} + \frac{1}{4}{\left( {a – 1} \right)^2} } = {1 + \frac{1}{4}{\left( {2 – 1} \right)^2} } = {1 + \frac{1}{4} } = {\frac{5}{4}.} n 2 = v 2 + 4 1 ( a –1 ) 2 = 1 + 4 1 ( 2–1 ) 2 = 1 + 4 1 = 4 5 .
بنابراین، جواب عمومی تابع z ( x ) z\left( x \right) z ( x )
y ( x ) = x – 1 2 z ( x ) = 1 x [ C 1 J 5 2 ( x ) + C 2 Y 5 2 ( x ) ] , {y\left( x \right) = {x^{ – \frac{1}{2}\normalsize}}z\left( x \right) } = {\frac{1}{{\sqrt x }}\left[ {{C_1}{J_{ \frac{{\sqrt 5 }}{2}\normalsize}}\left( x \right) }\right.}+{\left.{ {C_2}{Y_{ \frac{{\sqrt 5 }}{2}\normalsize}}\left( x \right)} \right],} y ( x ) = x – 2 1 z ( x ) = x 1 [ C 1 J 2 5 ( x ) + C 2 Y 2 5 ( x ) ] ,
که در آن، C 1 C_1 C 1 C 2 C_2 C 2
نمونه سوال معادلات دیفرانسیل ۳۶
جواب عمومی معادله دیفرانسیل زیر را برای ∣ x ∣ < 1 \left| x \right| \lt 1 ∣ x ∣ < 1
( 1 – x 2 ) y ′ ′ – x y ’ + 4 y = 0 \left( {1 – {x^2}} \right)y^{\prime\prime} – xy’ + 4y=0 ( 1– x 2 ) y ′′ – x y ’ + 4 y = 0
حل سوال ۳۶: این معادله یک معادله چبیشف و پارامتر چبیشف آن، n = 2 n = 2 n = 2
y ( x ) = C 1 cos ( 2 arccos x ) + C 2 sin ( 2 arccos x ) {y\left( x \right) }={ {C_1}\cos \left( {2\arccos x} \right) }+{ {C_2}\sin\left( {2\arccos x} \right)} y ( x ) = C 1 cos ( 2 arccos x ) + C 2 sin ( 2 arccos x )
که در آن، C 1 C_1 C 1 C 2 C_2 C 2
جواب را با چندجملهای چبیشف نوع اول قابل بیان است. از آنجا که:
cos ( 2 arccos x ) = T 2 ( x ) = 2 x 2 – 1 {\cos \left( {2\arccos x} \right) = {T_2}\left( x \right) }={ 2{x^2} – 1} cos ( 2 arccos x ) = T 2 ( x ) = 2 x 2 –1
جواب نهایی بهشکل زیر خواهد بود:
y ( x ) = C 1 cos ( 2 arccos x ) + C 2 1 – cos 2 ( 2 arccos x ) = C 1 T 2 ( x ) + C 2 1 – T 2 2 ( x ) = C 1 ( 2 x 2 – 1 ) + C 2 1 – ( 2 x 2 – 1 ) 2 = C 1 ( 2 x 2 – 1 ) + 2 C 2 x 1 – x 2 . {y\left( x \right) }={ {C_1}\cos \left( {2\arccos x} \right) }+{ {C_2}\sqrt {1 – {\cos^2}\left( {2\arccos x} \right)} } \\ = {{C_1}{T_2}\left( x \right) + {C_2}\sqrt {1 – T_2^2\left( x \right)} } \\ = {{{C_1}\left( {2{x^2} – 1} \right) }+{ {C_2}\sqrt {1 – {{\left( {2{x^2} – 1} \right)}^2}} }} \\ = {{{C_1}\left( {2{x^2} – 1} \right) }+{ 2{C_2}x\sqrt {1 – {x^2}} .}} y ( x ) = C 1 cos ( 2 arccos x ) + C 2 1– cos 2 ( 2 arccos x ) = C 1 T 2 ( x ) + C 2 1– T 2 2 ( x ) = C 1 ( 2 x 2 –1 ) + C 2 1– ( 2 x 2 –1 ) 2 = C 1 ( 2 x 2 –1 ) + 2 C 2 x 1– x 2 .
جمعبندی نمونه سوال معادلات دیفرانسیل
در این آموزش، با تعدادی نمونه سوال معادلات دیفرانسیل آشنا شدیم. برای تسلط بیشتر بر حل نمونه سوال معادلات دیفرانسیل ، میتوانید مجموعه آموزشهای فرادرس را تهیه کنید که در آنها، نمونه سوال معادلات دیفرانسیل کنکور کارشناسی ارشد نیز حل شده است.



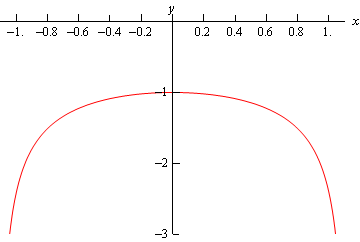

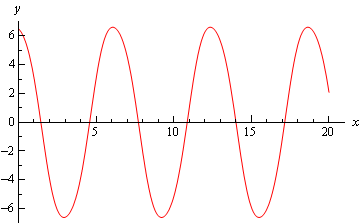

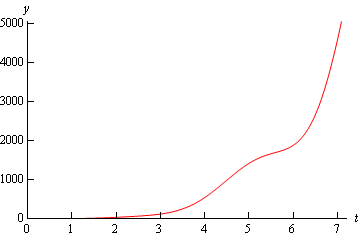

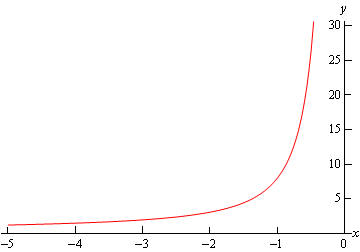

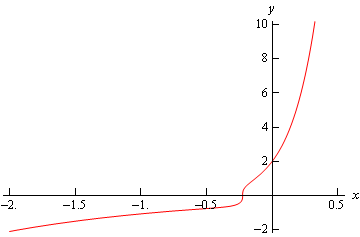



















با سلام
احتراماً به استحضار میرساند که طی مطالعه معادلات دیفرانسل و تمارین مربوطه متاسفانه در سیستم تمام فرمول های مربوطه و صورت سوال دارای خطا Math Processing Error نمایش می دهد. لطفا جهت مطالعه متن، راهنمایی لازم جهت رفع خطا Error را بازگو نمایید.
با تشکر از پیگیری و راهنمایی شما
با سلام؛
این مورد پیگیری و اصلاح شد.
با تشکر از همراهی شما با مجله فرادرس