نمودار هسه و مجموعه مرتب جزئی | مفاهیم و نحوه رسم

یکی از روش‌های نمایش «مجموعه‌های مرتب جزئی متناهی» (Finite Partially Orders Set) در ریاضیات، رسم «نمودار هسه» (Hasse Diagram) است که به صورت بالارونده (Upward Orientation) ترسیم می‌شود. به علت اینکه این بیان تصویری در بسیاری از الگوریتم‌های جستجو و مرتب‌سازی نیز مورد استفاده است، این نوشتار از مجله فرادرس را حول محور نمودار هسه به پیش خواهیم برد.

برای آشنایی بیشتر با مباحث مربوط به نظریه مجموعه‌ها و ترتیب‌ها بهتر است مطالب رابطه و تابع از نگاه مجموعه‌ ها — به زبان ساده و نظریه مجموعه در ریاضیات | مفاهیم اولیه و کاربردها را مطالعه کنید. همچنین خواندن نوشتارهای نمایش ماتریسی گراف — به زبان ساده و معکوس تابع و تابع معکوس — به زبان ساده نیز خالی از لطف نیست.

نمودار هسه و مجموعه مرتب جزئی

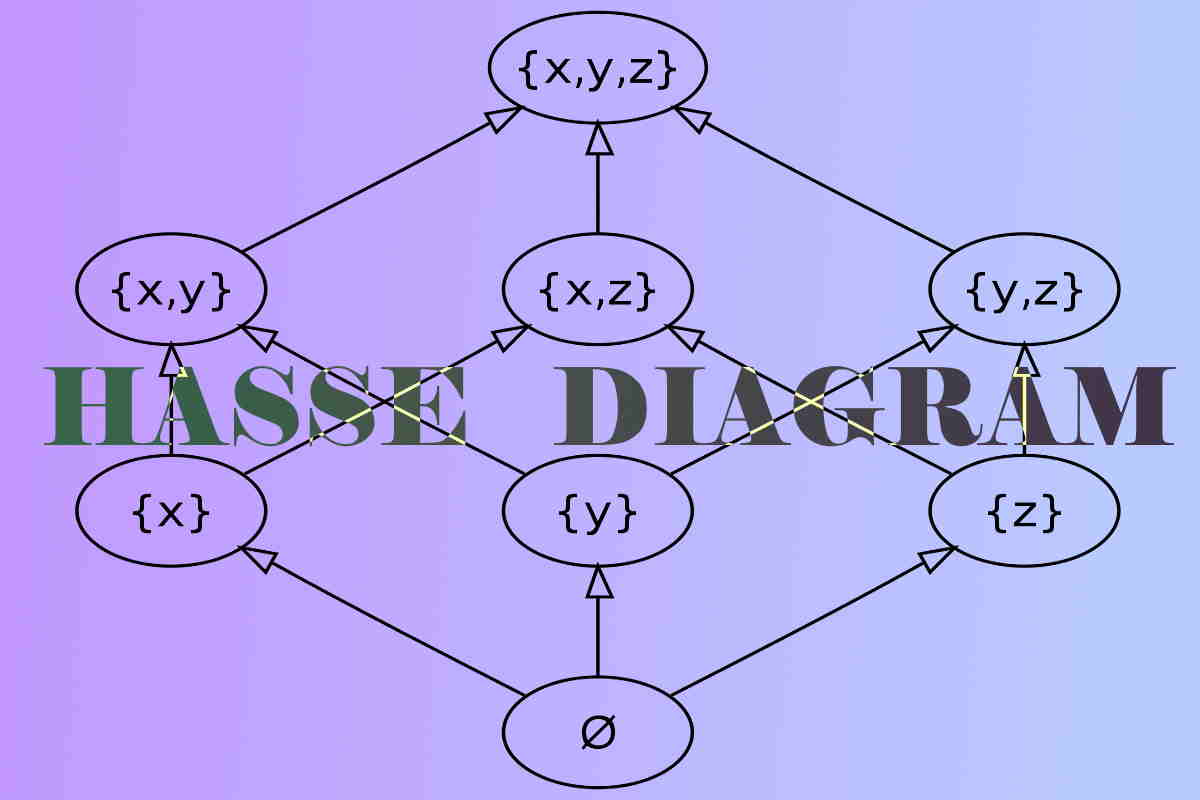
مجموعه‌ای مانند $$S$$ و یک «رابطه ترتیب جزئی» (Partial Order) را در نظر بگیرد. هر مولفه یا عضو از مجموعه $$S$$، یک «راس» (Vertex) یا گره در نمودار هسه محسوب شده و خطوط ترسیمی بین راس‌ها یا گره‌ها، نشانگر وجود رابطه ترتیبی بین این اعضا هستند. در تصویر ۱، نمونه‌هایی از نمودار هسه را در «جبر بول» (Boolean Algebra) مشاهده می‌کنید. در قسمت پایینی این تصویر، رابطه‌ها دارای جهت نیستند. ولی در قسمت بالایی تصویر ۱، برای هر بردار در گراف ترسیم شده، جهت در نظر گرفته شده است.

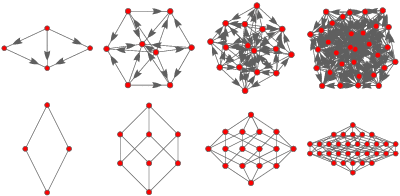
البته در ادامه خواهید خواند که رابطه ترتیب جزئی به علت داشتن خاصیت پادتقارنی، نمی‌تواند دارای جهت دو طرفه باشد. ولی از آنجایی که نمودار هسه ذاتا یک نمودار جهت دار (از پایین به بالا) است، اغلب در ترسیم این نمودار از مشخص کردن جهت‌ها، خودداری می‌کنند.

فیلم آموزش ساختمان گسسته – مرور و حل تست های کنکور کارشناسی ارشد در فرادرس

کلیک کنید

این نمودار اولین بار توسط «هلمون هسه» (Helmut Hasse)، ریاضیدان آلمانی، برای نمایش مجموعه‌های مرتب جزئی در نیمه دوم قرن بیستم معرفی شد. قبل از هر چیز، برای آنکه بهتر رابطه نمایش داده شده در نمودار هسه را درک کنیم، در مورد اصطلاح «مجموعه مرتب جزئی» (Partially Ordered Set) توضیحاتی ارائه خواهیم کرد.

ترتیب جزئی و مجموعه مرتب جزئی

یک مجموعه مرتب جزئی یا به طور خلاصه Poset (مخفف سه عبارت Partially Ordered Set)، به صورت یک مجموعه مثل $$S$$ و یک رابطه ترتیب جزئی، مثلا با نماد $$\leq$$ مشخص می‌شود. اعضای چنین مجموعه‌ای در رابطه‌های زیر صدق می‌کنند.

• رابطه بازتابی یا انعکاسی (Reflexive Relation): در یک Poset، هر عضوی با خودش دارای رابطه ترتیب جزئی $$\leq$$ است. در نتیجه می‌توان نوشت:

$$ \large {\displaystyle \forall x \in S,\;\;\;\; x \leq x } $$

• رابطه پادتقارنی (Antisymmetric Relation): دو عضو $$x,y$$‌ از یک مجموعه مرتب جزئی، در رابطه زیر صدق می‌کنند. در این حالت رابطه‌ $$\leq$$ را پادتقانی می‌نامند.

$$ \large {\displaystyle \forall x, y \in S,\;\;\;\; (x \leq y) \text{ AND } (y \leq x) \longleftrightarrow x = y } $$

• رابطه ترایا (Transitive Relation):  این بار سه عضو از مجموعه مرتب جزئی مثل $$x,y,z$$ را در نظر بگیرید. رابطه زیر بین آن‌ها در یک Poset برقرار است.

$$ \large {\displaystyle \forall x , y, z \in S, \;\;\; x \leq y , \;\;\; y \leq  z \longrightarrow x \leq z } $$

نکته: هر رابطه‌ای ترتیب جزئی مثل $$R$$ که روی مجموعه $$S$$، هر سه نوع ویژگی بالا را داشته باشد، یک رابطه ترتیبی روی آن مجموعه ایجاد خواهد کرد و فضای $$(S , R)$$ را یک مجموعه مرتب جزئی می‌نامند. اغلب برای نمایش چنین مجموعه‌ای از نمودار هسه استفاده می‌کنند. حال، با توجه به این موضوعات، به بررسی نحوه ترسیم نمودار هسه خواهیم پرداخت.

رسم نمودار هسه

همانطور که در تصویر ۱، مشاهده کردید، نمودار هسه یک نمودار از «پایین به بالا» (Upward Orientation) است. به این معنی که نقطه‌ها یا گره‌ها باید از پایین به بالا، مورد جستجو قرار گیرند. با توجه به قواعدی که در ادامه گفته خواهد شد، نمودار هسه برای نمایش ارتباط بین اعضای یک Poset یا یک مجموعه مرتب جزئی، ترسیم می‌شود.

• برای دو عنصر مثل $$x , y$$ از Poset، اگر $$x < y$$ باشد، نقطه یا گره مربوط به $$x$$، پایین‌تر از نقطه $$y$$ نمایش یا ترسیم می‌شود.
• در نمودار هسه، دو نقطه $$x$$ و $$y$$ از مجموعه مرتب جزئی، در صورتی به یکدیگر مرتبط هستند که بین آن‌ها رابطه ترتیبی $$\leq$$ برقرار باشد و برعکس. به این ترتیب اگر خطی بین دو نقطه یا گره در نمودار هسه، ترسیم شده باشد، نشانگر وجود رابطه ترتیبی بین آن‌ها است.

این بار به کمک توضیحات ارائه شده، در قالب چند مثال، به رسم نمودار هسه برای یک مجموعه مرتب جزئی می‌پردازیم. البته توجه داشته باشید که هر یک از رابطه‌های معرفی شده در مثال‌های زیر، یک رابطه ترتیب جزئی بوده و خصوصیات بازتابی، پادتقارنی و ترایا را دارند. بررسی این ویژگی‌ها البته ساده هستند ولی انجام محاسبات و نمایش این خصوصیات را به عهده خواننده می‌گذاریم.

مثال ۱

مجموعه مرتب جزئی زیر را در نظر بگیرید.

$$ \large {\displaystyle (\{3 , 4 , 12 , 24 , 48 , 72\} , / ) } $$

فیلم آموزش ریاضیات گسسته در فرادرس

کلیک کنید

فرض کنید که رابطه $$\prec$$ تحت عملگر $$/$$ که همان رابطه تقسیم‌پذیری یا عاد کردن است، ایجاد یک ترکیب کند. در این صورت می‌توان اعضای Poset را به صورت زیر در نظر گرفت.

$$ {\displaystyle \begin{align} A =& \{(3 \prec 12), (3 \prec 24), (3 \prec 48), (3 \prec 72), (4 \prec 12), (4 \prec 24), (4 \prec 48), (4 \prec 72) \\ &, (12 \prec 24), (12 \prec 48), (12 \prec 72), (24 \prec 48), (24 \prec 72)\} \end{align} }$$

واضح است که ۳ با همه اعضای این مجموعه به جز ۴، در رابطه تقسیم‌پذیری صدق می‌کند. تعداد عناصری که بر هر یک از اعضا، بخش‌پذیر باشد، ترتیب را مشخص کرده و نحوه قرارگیری عناصر را در نمودار هسه مشخص می‌کند.

در واقع، ۳ فقط به خودش بخش پذیر است. از طرفی ۴ نیز فقط بر ۴ بخش‌پذیر بوده در نتیجه تعداد عناصری از این مجموعه که بر این دو مقدار بخش‌پذیر هستند، برابر با یک بوده و این دو مقدار در پایین‌ترین سطح نمودار ظاهر می‌شوند.

نکته: هر عضوی از مجموعه، با خودش در ارتباط بخش‌پذیری است. در نتیجه خاصیت بازتابی برقرار است. از طرفی مشخص است که خاصیت بخش‌پذیری روی این مجموعه، دارای ویژگی پادتقارنی است. یعنی در صورتی که $$x$$ بر $$y$$‌ بخش پذیر بوده و $$y$$ نیز بر $$x$$ بخش‌پذیر باشد، آنگاه باید $$x=y$$ باشد. همچنین طبق قضیه‌های هم‌نهشتی می‌توان نشان داد که اگر $$x$$، عدد $$y$$ را عاد کند و $$y$$ نیز بر $$z$$ بخش‌پذیر باشد، آنگاه $$x$$ نیز $$z$$ را عاد می‌کند. پس رابطه تقسیم‌پذیری یک رابطه ترتیبی است.

به این ترتیب نمودار هسه برای چنین مجموعه‌ای به صورت زیر خواهد بود.

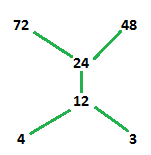
از این جهت گره یا نقطه ۳ و ۴ را در یک سطح قرار داده‌ایم، تا نشان دهیم که تعداد عناصر بخش‌پذیر بر آن‌ها یکسان است. از طرفی هیچ یک با هم رابطه نیز ندارند. در حقیقت می‌توان آن‌ها را نسبت به یکدیگر اول یا متباین (Coprime) در نظر گرفت.

از طرفی تعداد مقسوم‌های عدد ۱۲ برابر با ۲ است. همچنین با توجه به تقسیم‌پذیری ۱۲ بر ۳ و ۴، هر دو گره را به ۱۲ متصل کرده‌ایم، زیرا هر دو با ۱۲ در ارتباط بخش‌پذیری هستند. برای گره یا عضو ۲۴، واضح است که تعداد مقسوم‌های آن سه عضو یا عنصر از مجموعه Poset است. در نتیجه بالاتر از ۱۲ قرار گرفته و از طریق ۱۲ به دو گره ۳ و ۴ نیز متصل است.

در انتها، چون ۴۸ و ۷۲، هر دو دارای چهار مقسوم علیه هستند در یک سطح و بالاتر از ۲۴ دیده می‌شوند. همچنین چون هیچ یک، مقسوم علیه دیگری نیز نیست، نمی‌توان آن‌ها را به هم وصل کرد.

مثال ۲

مجموعه مرتب جزئی به صورت $$(D_{12},/)$$ را در نظر بگیرد. منظور از $$D_{12}$$، مجموعه همه مقسوم‌علیه‌های عدد ۱۲ است. در این حالت چنین مجموعه‌ای را به صورت زیر نمایش می‌دهیم.

$$ \large {\displaystyle D_{12} = \{1, 2, 3, 4, 6, 12 \} } $$

به این ترتیب مجموعه مرتب جزئی به شکل زیر خواهد بود.

$${\displaystyle \begin{align} A = & \{(1 \prec 2), (1 \prec 3), (1 \prec 4), (1 \prec 6), (1 \prec 12), (2 \prec 4), (2 \prec 6), (2 \prec 12), (3 \prec 6)\\ , & (3 \prec 12), (4 \prec 12), (6 \prec 12) \} \end{align} }$$

فیلم آموزش ریاضیات گسسته – حل تست کنکور کارشناسی ارشد در فرادرس

کلیک کنید

باز هم برای نمایش رابطه تعداد مقسوم‌علیه‌های و مقایسه آن‌ها برای اعضای مجموعه از $$\prec$$ استفاده کرده‌ایم. با توجه به مثال قبل، نمودار هسه برای چنین مجموعه مرتب جزئی به صورت زیر در خواهد آمد.

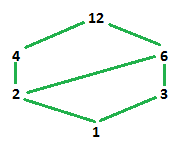
از آنجایی که عدد ۱، با همه عناصر دیگر در رابطه تقسیم صدق کرده و از همه نیز کوچکتر است، در پایین نمودار قرار گرفته است. واضح است که مقسوم‌علیه‌های ۲ و ۴ در یک طرف و مقسوم‌علیه‌های ۶ و ۳ نیز در طرف دیگر نمودار ظاهر خواهند شد. زیرا ۴ با ۶ در رابطه نیست. خط ارتباطی بین ۲ و ۶ به این علت ترسیم شده که ۲ مقسوم علیه ۶ بوده و با آن در ارتباط است. ترتیب قرارگیری این مقسوم‌علیه‌ها هم از کوچک به بزرگ تنظیم شده است.

پس این نمودار دارای یک راس ابتدایی (با مقدار ۱) و یک راس انتهایی (با مقدار ۱۲) خواهد بود.

ویژگی‌های اصلی یک نمودار هسه

هر نمودار هسه عادی، دارای خواصی است که در ادامه فهرست می‌شوند. مشخص است که نمودارهای ترسیم شده برای مثال ۱ و ۲ نیز این گزاره‌ها را مورد تایید قرار می‌دهند.

• عناصر ماکزیمال: هر نمودار هسه دارای یک یا چند «عنصر ماکزیمال» (Maximal Elements) است. عنصری که در بالاترین سطح قرار گرفته و هیچ عنصری بعد از آن در نمودار دیده نشود، عنصر ماکزیمال نامیده می‌شود. در مثال ۱، عناصر ماکزیمال، ۴۸ و ۷۲ بودند. همچنین در مثال ۲ نیز، ۱۲ عنصر ماکزیمال است.
• عناصر مینیمال: عناصری از نمودار هسه که هیچ عنصری پیش از آن‌ها وجود نداشته باشد، «عنصر مینمال» (Minimal Elements) گفته می‌شود. در مثال اول، عناصر ۳ و ۴، عناصر مینیمال بودند. همچنین در مثال ۲ نیز مقدار ۱ عنصر مینیمال نامیده می‌شود.
• بیشترین عنصر: در صورت وجود فقط یک عنصر به عنوان راس نمودار، آن را «بیشترین عنصر» (Greatest Element) می‌نامیم. واضح است که همه عناصر دیگر پایین‌تر از بیشترین عنصر در نمودار هسه قرار می‌گیرند. البته ممکن است چنین عنصری وجود نداشته باشد. در مثال ۱ بیشترین عنصر وجود ندارد در حالیکه در مثال ۲، ۱۲ بیشترین عنصر محسوب می‌شود.
• کمترین عنصر: کمترین مقدار یا پایین‌ترین گره در نمودار هسه را «کمترین عنصر» (Least Element) می‌گوییم. در حقیقت همه عناصر دیگر در بالای کمترین عنصر در نمودار هسه ظاهر می‌شوند. در مثال ۱ کمترین عنصر وجود نداشته ولی در مثال ۲، عدد یا گره ۱ کمترین عنصر است.

نکته: توجه داشته باشید که کمترین عنصر یا بزرگترین عنصر در صورت وجود، یکتا هستند.

باید توجه داشت که رسم نمودار هسه به صورت یکتا میسر نیست و می‌توان برای یک مجموعه مرتب جزئی، نمودار هسه را به اشکال مختلف ترسیم کرد. در مثال ۳ به این موضوع اشاره خواهیم داشت.

مثال ۳

یک مجموعه مثل $$A$$ با ۴ عنصر را در نظر بگیرید. «مجموعه توانی» (Power Set) حاصل از $$A$$ را به صورت $$P(A)$$ نشان می‌دهیم. مجموعه توانی با رابطه ترتیب جزئی زیرمجموعه (Subset) با نماد $$\subseteq$$ تشکیل یک مجموعه مرتب جزئی می‌دهند.

توجه داشته باشید که رابطه «زیرمجموعه»، یک رابطه ترتیب جزئی است، زیرا روابط زیر برایش برقرار است.

بازتابی است، یعنی داریم:

$$\large \forall X \in P(A) , \;\;\; X \subseteq X $$

دارای خاصیت پادتقارنی نیز هست، چون:

$$\large \forall X, Y  \in P(A) , \;\;\; (X \subseteq Y) \text{  AND  } (Y \subseteq X) \; \rightarrow \;  X = Y $$

از طرفی خاصیت ترایایی نیز دارد.

$$\large \forall X, Y,Z  \in P(A) , \;\;\; (X \subseteq Y) \text{  AND  } (Y \subseteq Z) \; \rightarrow \;  X \subseteq Z $$

فرض کنید مقدار ۰ نشانگر آن باشد که یک عنصر در زیر مجموعه حضور ندارد و همچنین مقدار ۱ نیز حضور آن را در زیرمجموعه نشان دهد. در این صورت طبق رابطه ترتیب جزئی برای مجموعه $$P(A)$$، نمودار هسه به صورت زیر در خواهد آمد.

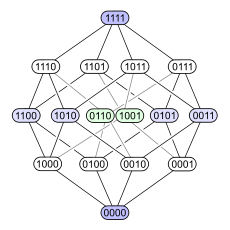
هر گره، نشانگر یک زیر مجموعه است که رابطه زیر مجموعه بودن و ترتیب قرارگیری آن‌ها را نشان می‌دهد. پایین‌ترین گره، همان مجموعه تهی است که برای همه عناصر، مقدار صفر را دارد.

فیلم آموزش ساختمان گسسته با رویکرد حل مساله در فرادرس

کلیک کنید

همچنین در بالاترین سطح نیز خود مجموعه اصلی قرار گرفته که همه عنصرها در آن دیده می‌شوند، زیرا دارای ۴ مقدار ۱ متناظر با چهار عنصر مجموعه $$A$$ است. در بین این دو گره، زیرمجموعه‌های تک عضوی، دو عضوی و سه عضوی قابل مشاهده هستند.

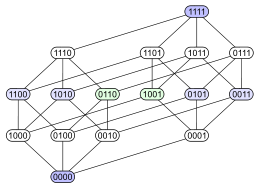
این مجموعه مرتب جزئی را به صورت یک نمودار هسه دیگر که در تصویر ۵ ترسیم شده نیز می‌توان نشان داد. همانطور که می‌بینید، این امکان وجود دارد که یک مجموعه مرتب جزئی را به چندین شیوه متفاوت توسط نمودار هسه نمایش داد که البته همگی معادل یا هم‌ارز هستند.

خلاصه و جمع‌بندی

در این نوشتار به مجموعه مرتب جزئی و همچنین نحوه ترسیم ارتباط یا رابطه‌ها بین اجزای آن توسط نمودار هسه پرداختیم. همچنین در قسمتی از متن، خصوصیات یک نمودار هسه مناسب را بازگو کردیم. هر چند نمودار هسه برای نمایش مجموعه‌های مرتب جزئی مناسب است ولی مشکل آن است که نحوه ترسیم آن به شیوه‌ها و شکل‌های گوناگون امکان‌پذیر خواهد بود. شاید این امر نحوه مقایسه و تشخیص برابری آن‌ها را دشوار کند.