نمایش ناهنجاری و الگوریتم جنگل ایزوله با پایتون | راهنمای کاربردی
صعود و فرودهای ناگهانی برای یک اندازه یا متغیر نشانگر ناهنجاری یا رفتار نامتعارف برای یک پدیده است. نقاط فرورفتگی و هم برجستگیها نیز در نمودار مربوط به تغییرات یک پدیده در زمان، نشانگر وجود نقاط پرت یا دورافتاده است. اگر ما قبل از مدلسازی اطلاعاتی در مورد رفتار غیرعادی یک متغیر داشته باشیم، میتوان با اجرای «الگوریتمهای یادگیری نظارتی» (Supervised Learning Algorithms) مشکل وجود ناهنجاری را حل کرد، اما متاسفانه در ابتدا امر و زمانی که با دادهها مواجه هستیم، تشخیص آنها کار دشواری است. این مشکل ممکن است به نارسایی در مدل بیانجامد. به همین دلیل نمایش و شناسایی ناهنجاری قبل از مدل سازی روی دادهها امری ضروری است. در ادامه به کمک محاسبات و ترسیم نمودارهایی، قصد داریم از زبان پایتون و کتابخانههای آن برای نمایش ناهنجاری با الگوریتم جنگل ایزوله استفاده کنیم.

یکی از الگوریتمهای محبوب و البته کارا در زمینه شناسایی نقاط ناهنجار، «الگوریتم جنگل ایزوله» (Isolation Forest Algorithm) است. به منظور آشنایی با این الگوریتم بهتر است ابتدا نوشتارهای دیگر مجله فرادرس مانند الگوریتم جنگل ایزوله — راهنمای کاربردی و تشخیص ناهنجاری (Anomaly Detection) — به زبان ساده را مطالعه کنید. همچنین خواندن نوشتارهای الگوریتم جنگل ایزوله در پایتون — راهنمای کاربردی و مشاهده ناهنجار و شناسایی آن در SPSS — راهنمای کاربردی نیز خالی از لطف نیست.
نمایش ناهنجاری و الگوریتم جنگل ایزوله
همانطور که گفته شد، الگوریتمهای یادگیری نظارت شده به سختی قادر به نمایش ناهنجاری یا نقاط نامتعارف در دادهها هستند، زیرا نقاط از ابتدا به دو گروه هنجار و ناهنجار تفکیک یا افراز نشدهاند. در نتیجه «الگوریتمهای یادگیری غیرنظارتی» (Unsupervised Learning Algorithm) بخصوص روشهایی مانند «جنگل ایزوله» (Isolation Forest) که به اختصار IF نامیده شده همچنین تکنیک «ماشین بردار پشتیبان» (Support Vector Machine) که به اختصار SVM گفته میشوند، کارایی مناسبی دارند.
در ادامه به کمک ترسیم نمودارها و استفاده از الگوریتم IF سعی در شناسایی نقطههای ناهنجار در یک مجموعه داده خواهیم کرد. به این ترتیب یک محقق میتواند ناهنجاریها را در یک مجموعه داده تصادفی، تشخیص داده و با تحلیل نمودارها، چنین مشاهداتی را به طور مجزا و جداگانه مورد بررسی قرار میدهد. از طرفی او باید برای مدل سازی از مجموعه دادههای آموزشی بدون این نقطهها بهره ببرد.
بدون کمک بازخورد (Feedback)، تشخیص این گونه نقاط، کاری دشوار است. بنابراین ما با استفاده از الگوریتمهایی مانند Isolation Forest ، One class SVM و LSTM این مسئله را به عنوان یک مدل «غیرنظارتی» (Unsupervised Model) در نظر میگیریم. البته در ادامه این متن با استفاده از الگوریتم جنگل ایزوله یا IF، عمل خواهیم کرد.
اطلاعات مربوطه در اینجا برای هر مشاهده با ۱۲ متغیر (به عنوان مثال درآمد، ترافیک و غیره) مشخص میشوند. ابتدا باید تشخیص دهیم که آیا یک ناهنجاری در سطوح مختلف مشاهدات وجود دارد یا خیر. سپس برای عملکرد بهتر، به معیارها و ویژگیهای خاص مشاهدات به صورت جداگانه میپردازیم و ناهنجاریهای موجود در هر یک از متغیرها را شناسایی میکنیم.
کد زیر به منظور بارگذاری فایل داده و نصب کتابخانههای مورد نیاز در زبان برنامهنویسی پایتون نوشته شده است. توجه داشته باشید که دادههای به طور تصادفی ایجاد شده و در فایلی به نام metric_data.csv ذخیره شدهاند. شما نیز میتوانید چنین فایلی را به کمک توابع تصادفی در پایتون ایجاد کنید. البته توزیع تولید این دادهها به شکلی است که نقاط پرت تولید میشوند. در حقیقت بهتر است چنین دادههایی را از توزیعهای پایدار (Stable Distribution) با تولید کنید.
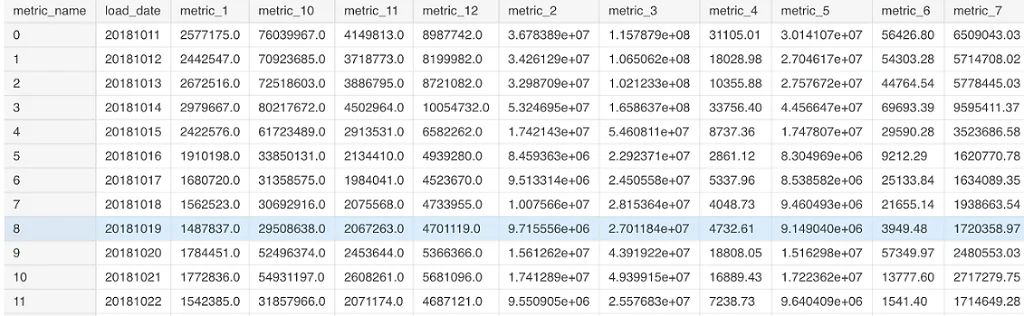
تصویر 1، نشانگر تعدادی از متغیرهای مربوطه برای مشاهدات اولیه این مجموعه داده (Dataframe) است.
حالا یک تغییر محوری روی چارچوب داده، اجرا کرده و متغیرها را در سطوح مختلف مقادیر تاریخی ایجاد میکنیم. کد زیر به این منظور نوشته شده است.
نتیجه اجرای این کد، تولید یک چارچوب داده جدید به اسم metrics_df است که در تصویر ۲، قسمتی از دادههای آن را مشاهده میکنید.
الگوریتم جنگل ایزوله سعی دارد نقاط ناهنجار را از این مجموعه داده استخراج کند. اگر هر متغیر (metric_i) را برحسب زمان ترسیم کنیم، یک نمودار خطی حاصل میشود که مطابق با آن رفتار و تغییرات متغیرها قابل مشاهده است. به این ترتیب نقطههایی که رفتار متفاوت با بقیه نقاط دارند شناسایی میشوند. در حقیقت این نقاط در قلهها یا فرورفتگیهای عمیق منحنی قرار خواهند گرفت. در مقابل نقاط هنجار در کنار یکدیگر بوده و روند کلی منحنی را نمایش میدهند. در ادامه به کدهایی اشاره خواهیم کرد که با استفاده از الگوریتم جنگل ایزوله، در کتابخانه sklearn نمایش ناهنجاری را به شکل جداگانه روی یک نمودار دو بعدی نمایش خواهد داد.
نکته: در اینجا برای هر متغیر به شکل مجزا، از الگوریتم جنگل ایزوله استفاده میکنیم. ولی الگوریتم بهینه شده h2o که برگرفته از IF است، قادر به محاسبات روی دادههای حجیم و با ابعاد بالا است که در نوشتارهای دیگر مجله فرادرس به آن نیز خواهیم پرداخت.
در تصویر زیر تعداد نقاط ناهنجار که با کد ۱- مشخص شدهاند، نمایش داده شده است.

کاهش ابعاد با تکنیک PCA
همانطور که میدانید، ۱۲ متغیر در چارچوب داده (DataFrame) وجود دارد. بنابراین باید بر حسب هر یک از آنها نقاط ناهنجار را مشخص کنیم. البته این کار با توجه به ابعاد مسئله و وجود همبستگی (Correlation) بین بعضی از متغیرها، ممکن است مشکلساز شود.
برای کاهش تعداد ابعاد، متغیرها را با تکنیک تحلیل مولفههای اصلی (PCA) تبدیل کرده و به مولفههایی با کمترین همبستگی و البته با بیشترین اطلاعات خواهیم رسید. در انتها نیز براساس سه مولفه اصلی که بیشترین توضیح برای دادهها خواهند بود، نموداری برای شناسایی نقاط ناهنجار معرفی شده توسط الگوریتم IF، ترسیم خواهیم کرد.
کدهایی مربوط به استخراج مولفههای PCA و رسم نمودار سه بعُدی در ادامه دیده میشود.
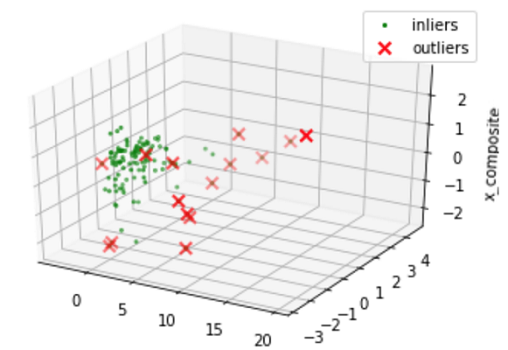
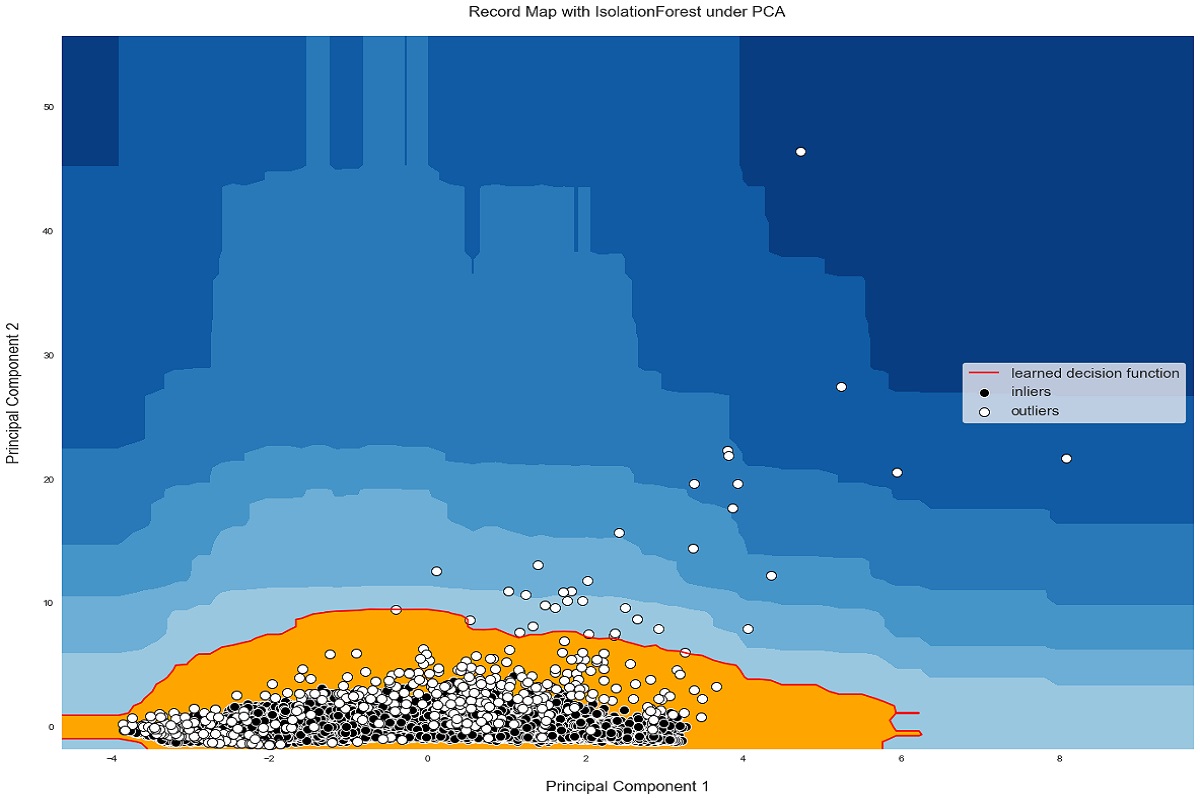
حالا همانطور که در نمودار مربوط به تصویر ۴، مشاهده میکنیم، نقاط ناهنجار با نقاط هنجار، که به صورت یک خوشه متمرکز در نمودار دیده میشوند، فاصله زیادی دارند. از طرفی نمودار دو بُعدی نیز به ما کمک میکند که نمایش ناهنجاری را بهتر کرده و دقیقتر قضاوت کنیم. اجازه دهید نمودار را برای حالت دو بُعدی برای دو مولفه دوم ترسیم کنیم.
کدی که در ادامه مشاهده میکنید به این منظور نوشته شده. همانطور که مشاهده میکنید، تعداد مولفهها را برابر با دو در نظر گرفته و به صورت (PCA(2 مشخص شده است.
نتیجه اجرای این کد، رسم نموداری است که در تصویر 5، قابل مشاهده است.
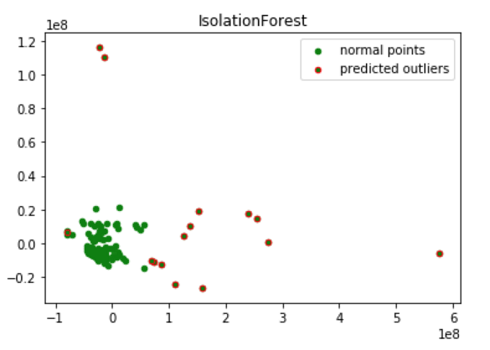
بنابراین یک نقشه 2D تصویر روشنی را به ما میدهد که الگوریتم نقاط ناهنجاری موجود را به درستی طبقهبندی کرده است. نمایش ناهنجاری به صورت نقاط قرمز رنگ در نمودار، برجسته شده و نقاط عادی با دایرههای سبز رنگ در این نمودار نمایان گردیده است.
نمایش ناهنجاری دو بعدی
اکنون ما رفتار نقاط ناهنجار را در هر یک از مولفهها شناختهایم و این راهکاری برای پیدا کردن مشاهدات ناهنجار است. نقاط ناهنجاری مشخص شده توسط الگوریتم، باید هنگام رسم نمودار دو بعُدی براساس متغیرها (Metrics) به صورت نقاط قلهها یا درهها دیده شوند که بیانگر پرش یا افت ناگهانی متغیرها است.
به منظور ترسیم نمودارهایی که این رفتارها را نشان دهند، کدهای زیر را تهیه کردهایم. در این جا هر یک از نقاط ناهنجار به همراه دیگر مشاهدات روی یک نمودار دو بُعدی ترسیم شده که محور افقی، زمان و محور عمودی، مقدار متغیر (Metric) است.
البته از آنجایی که دادهها چند بعُدی هستند، نمیتوان تنها به این نمودارها اکتفا کنیم. همانطور که در ابتدای متن خواندید، برای کاهش ابعاد از روش PCA استفاده کرده و براساس آنها نقاط ناهنجار را شناسایی کردیم. نمودارهای دو بعُدی ترسیم شده، نقش راهنما و یا تایید نتایج حاصل از اجرای الگوریتم IF را برای نمایش ناهنجاری دارند.
کد زیر به منظور دستهبندی متغیرها و نقش آنها در تعیین نقطه ناهنجار نوشته شده است. همچنین نقطهها براساس میزان ناهنجاری به سه دسته ۰- بدون ناهنجاری، ۱- ناهنجاری کم و ۲-ناهنجاری زیاد، طبقهبندی میشوند.
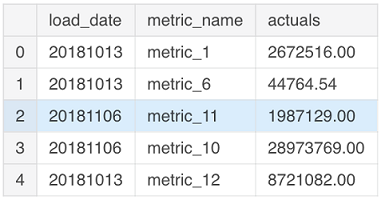
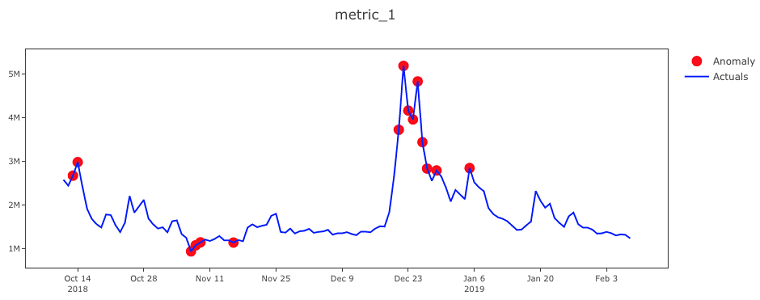
همانطور که در تصویر ۶، مشخص است محور X - تاریخ و محور Y - مقادیر واقعی و نقاط قرمز نیز ناهنجاری را مشخص کردهاند. مقادیر واقعی با خطوط آبی و نقاط ناهنجار با دایرههای قرمز رنگ در نمودار نسبت به دیگر نقاط، متمایز شدهاند.
در تصویر شماره ۷، نمایش ناهنجاری را به کمک متغیر 10_metric مشخص کردهایم. از آنجایی که هر دو این متغیرها در راستای یکدیگر تغییر میکنند، نقاط ناهنجار یکسانی را معرفی میکنند.
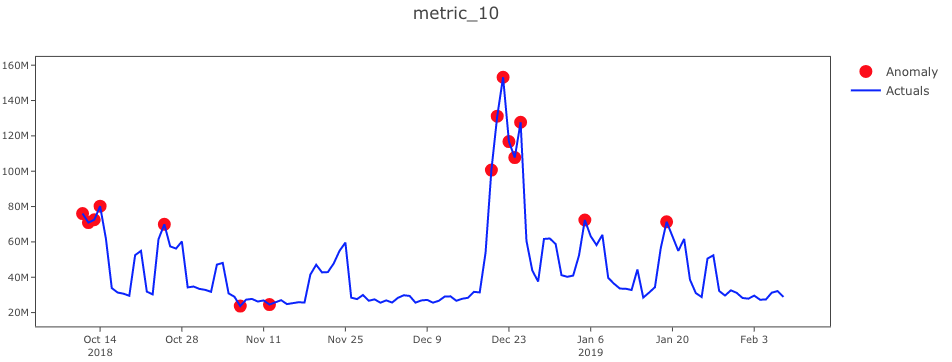
همانطور که دیده میشود، به کمک نمودارهای ترسیم شده، قلهها و فرورفتگیهای ناگهانی در هر یک از شاخصها، معرف نقاط ناهنجار خواهند بود. خوشبختانه، الگوریتم جنگل ایزوله نیز این نقاط را به درستی شناسایی کرده است.
خلاصه و جمعبندی
جنگل ایزوله یا جنگل جداسازی یک الگوریتم یا تکنیک تشخیص فاصله است که به جای مشاهدات عادی، بر ناهنجاریها تکیه دارد. الگوریتم جنگل ایزوله درست به مانند روشی که در جستجوی درخت باینری عمل میشود، وظیفه شناسایی نقاط یا نمایش ناهنجاری ها را انجام میدهد. در این نوشتار الگوریتم جنگل ایزوله در پایتون پیادهسازی شد و کارایی و قابلیتهای آن نیز به کمک مثالی با دادههای تصادفی مورد بررسی قرار گرفت. به منظور درک بهتر الگوریتم و نحوه جداسازی نقاط ناهنجار، از نمودارهایی در این زمینه استفاده کردیم.
در بیشتر الگوریتمها موجود در این زمینه، ویژگیهای دادههای متعارف و هنجار مشخص شده، سپس با توجه به تابع فاصله در نظر گرفته شده، نقاط ناهنجار و دورافتاده نسبت به آنها شناسایی میشوند. در حالیکه مطابق با الگوی به کار رفته در الگوریتم جنگل ایزوله، از همان ابتدا، هدف جداسازی و نمایش ناهنجاری است. به همین علت، دقت و البته سرعت اجرای الگوریتم جداسازی یا ایزوله کردن نقاط ناهنجار بسیار بیشتر است. همین امر نقطه قوت این الگوریتم در شناسایی نقطهها یا مشاهدات ناهنجار یا دورافتاده محسوب میشود.