الگوریتم جنگل ایزوله در پایتون — راهنمای کاربردی

شناسایی نقاط ناهنجار و نامتعارف در بین دادهها، کاری سخت و مشکل است. این امر زمانی که ابعاد دادهها نیز افزایش یابد، براساس الگوریتمها و روشها معمول، به دشواری صورت میگیرد. تکنیکهای جدید و روزآمد، مانند «الگوریتم جنگل ایزوله» (Isolation Forest Algorithm) بر این دشواریها چیره شده و با دقت و سرعت بیشتر قادر به انجام این کار هستند. به همین دلیل این نوشتار را به شناسایی داده ناهنجار با الگوریتم جنگل ایزوله در پایتون اختصاص دادهایم تا علاوه بر به کارگیری این الگوریتم، نحوه پیادهسازی آن را در پایتون نیز بیاموزیم. شایان ذکر است که در قسمت دوم از این نوشتار، الگوریتم جنگل ایزوله توسعه یافته (Extended Isolation Forest Algorithm) مورد بررسی قرار خواهد گرفت.
در این بین برای آشنایی بیشتر با چگونگی عملکرد الگوریتم جنگل ایزوله بهتر است نوشتارهای الگوریتم جنگل ایزوله — راهنمای کاربردی و تشخیص ناهنجاری (Anomaly Detection) — به زبان ساده را مطالعه کنید. همچنین خواندن مطالب مشاهده ناهنجار و شناسایی آن در SPSS — راهنمای کاربردی و رسم نمودار در پایتون با Matplotlib — راهنمای کاربردی نیز خالی از لطف نیست.
الگوریتم جنگل ایزوله در پایتون
بسیاری از الگوریتمهای یادگیری ماشین از نظر عملکرد با مشکل مواجه هستند زیرا مجموعه دادههای آموزشی (Training set) ممکن است شامل مشاهدات هنجار و ناهنجار باشند. به کارگیری نقاط ناهنجار، برآورد پارامترهای مدل را ممکن است دچار مشکل کرده و نتایج مناسب از مدل روی دادههای آزمایشی (Test Set)، صورت نگیرد.
به همین علت در عمل باید به بررسی دادههای هنجار پرداخته و نقطههایی که رفتار آنها با نقاط عادی یا هنجار مطابقت ندارند را به عنوان مشاهده ناهنجار شناسایی کرده و از دادههای آموزشی خارج کنیم.
از طرفی الگوریتمهای موجود در شناسایی مشاهدات ناهنجار با دو مشکل مواجه هستند. در ابتدای امر، زمانی را برای شناخت الگوی دادههای هنجار مصرف میکنند و سپس با به کارگیری توابع فاصله سعی در اندازهگیری فاصله همه نقاط از یکدیگر کرده و اگر این فاصله از مقدار آستانهای که براساس نقاط هنجار تعیین شده بیشتر باشد، آن مشاهدات را به عنوان نقاط ناهنجار معرفی میکنند.
در این بین به کارگیری تابع فاصله میتواند در تشخیص ناهنجاری مهم باشد. همانطور که میدانید «توابع فاصله» (Distance Functions)، تنوع زیادی دارند و انتخاب تابع فاصله مناسب از بین آنها میتواند در نتیجه تشخیص ناهنجاریها نقش زیادی داشته باشد.
الگوریتم جنگل ایزوله (ّIsolation Forest Algorithm) یا جنگل جداسازی (حتی به جنگل انزوایی نیز مشهور است) به خوبی از عهده این کار بر میآید. در این نوشتار میخواهیم، روشی که در اصل شبیه جنگل تصادفی (Random Forest) که روشی مشهور و محبوب است را به کار ببریم و به واسطه آن، نقاط نامتعارف را از مشاهدات عادی جدا کنیم.
اصول اولیه و نحوه عملکرد الگوریتم جنگل ایزوله
ایده اصلی در الگوریتم جنگل ایزوله، که متفاوت از سایر روشهای تشخیص ناهنجاریها است، در نحوه برخورد با دادههای آموزشی است. در این روش به جای بررسی و ایجاد پروفایل نقاط عادی و متعارف، صریحاً مشاهدات ناهنجار مشخص میشوند. جنگل ایزوله، مانند هر روش ساختار درختی (Tree Structure) دیگر، بر اساس درخت تصمیمگیری (Decision Tree) ساخته شده است. در این درختان، ابتدا تقسیمبندیهایی با انتخاب تصادفی یک ویژگی و سپس تعیین مقدار تقسیم تصادفی بین حداقل و حداکثر مقدار آن ویژگی انتخاب شده، صورت میگیرد.
در اصل، نقاط ناهنجار یا دورافتاده (Outlier) از لحاظ تعداد، کمتر از مشاهدات منظم و متعارف در مجموعه داده آموزشی هستند و از نظر مقادیر با آنها تفاوت زیادی دارند. به این معنی که چنین نقاطی از مشاهدات متعارف در فضای ویژگی فاصله میگیرند. به همین دلیل میتوان با استفاده از ایجاد تقسیمبندی تصادفی کمتر نسبت به شناسایی نقاط هنجار، آنها را به ریشه درخت نزدیکتر کرد. تقسیمهای لازم کشف ایده شناسایی مشاهدات ناهنجار در مقابل روشهای معمول شناسایی براساس نقاط هنجار در تصویر 1 مشخص شده است.
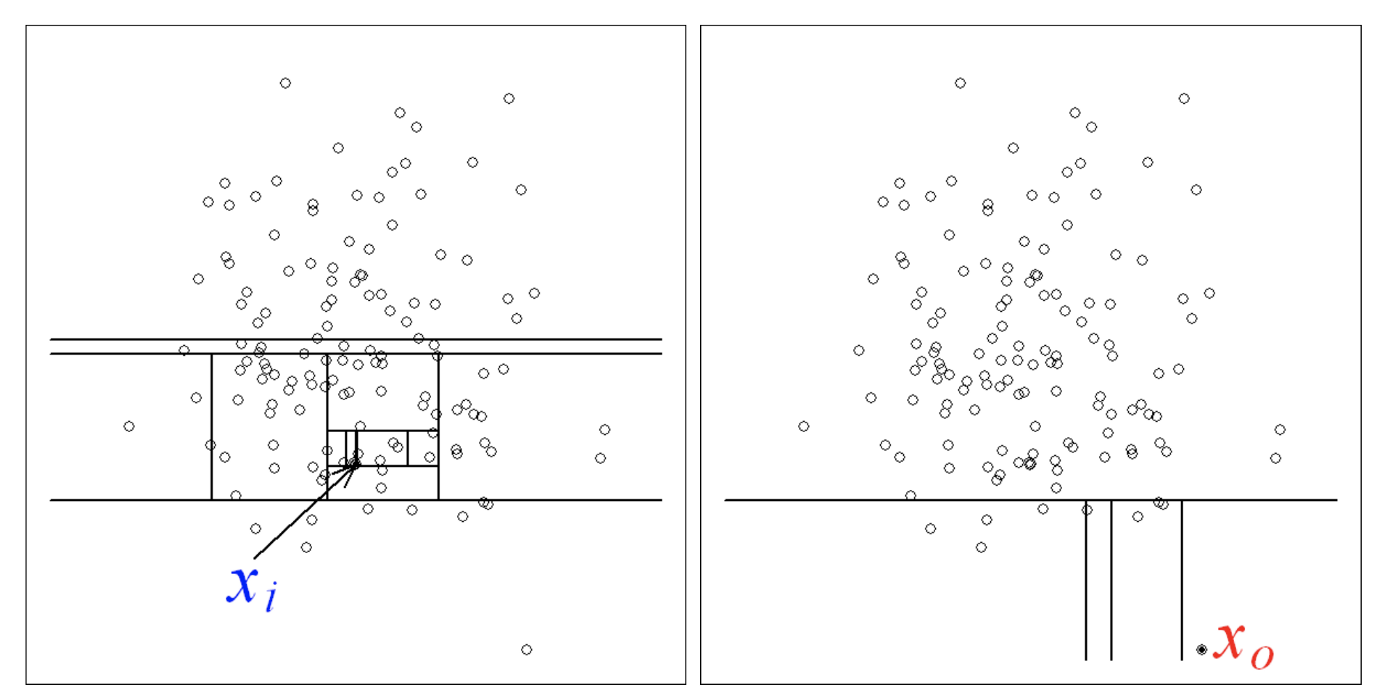
همانطور که در تصویر ۱ مشاهده میکنید، یک نقطه عادی (در سمت چپ) نیاز به شناسایی با تقسیمهای بیشتر دارد در حالیکه یک نقطه ناهنجار (سمت راست) با سرعت بیشتر و تقسیمات کمتر شناسایی میشود.
مانند سایر روشهایی که بر مبنایی تشخیص فاصله عمل میکنند، برای تصمیمگیری در مورد هر یک از نقاط، لازم است که یک امتیاز ناهنجاری محاسبه شود تا براساس آن چنین نقاطی تشخیص داده شوند. این شاخص در مورد جنگل ایزوله، اینگونه تعریف شده است:
توجه داشته باشید که طول مسیر در ساختار درختی برای مشاهده است و هم متوسط طول مسیر ناموفق در درخت جستجوی باینری (Binary Search) برای گره خارجی (External Node) است. برای مشاهده نحوه دقیق و شیوه محاسبه امتیاز ناهنجاری بهتر است نوشتار الگوریتم جنگل ایزوله — راهنمای کاربردی را مطالعه کنید.
به هر مشاهده نمره یا امتیاز ناهنجاری نسبت داده میشود و قاعده تصمیمگیری را میتوان بر اساس آن به شکل زیر اتخاذ کرد:
- نمره یا امتیاز ناهنجاری نزدیک به 1 نشان دهنده ناهنجاریها است.
- نمرات یا امتیاز ناهنجاری بسیار کوچکتر از 0.5 نشان دهنده مشاهدات عادی است.
- اگر تمام نمرات یا امتیازهای ناهنجاری نزدیک به 0.5 باشد، به نظر نمیرسد که کل دادههای آموزشی ناهنجاری داشته باشند.
پیاده سازی الگوریتم جنگل ایزوله در پایتون
حال زمان آن رسیده که به کمک یک مثال عملی و با دادههای شبیه سازی شده، الگوریتم جنگل ایزوله در پایتون را به کمک کدهایی پیادهسازی کنیم. خوشبختانه در پایتون کتابخانهای برای اجرای این الگوریتم در نظر گرفته شده است.
در این بین از دادههای تصادفی استفاده کرده و دو دسته از مقادیر یکی به عنوان مجموعه دادههای آموزشی (Training Set) و یکی به عنوان مجموعه دادههای آزمایشی (Test Set) ایجاد میکنیم.
همانطور که در کد زیر مشاهده میکنید، کتابخانههای numpy و pandas را برای انجام محاسبات فراخوانی کرده و از matplotlib نیز برای رسم نمودارها کمک گرفتهایم. همچنین برای راهاندازی الگوریتم جنگل ایزوله در پایتون از کتابخانه scikit-learn استفاده خواهیم کرد.
1# importing libaries ----
2import numpy as np
3import pandas as pd
4import matplotlib.pyplot as plt
5from pylab import savefig
6from sklearn.ensemble import IsolationForest
7# Generating data ----
8
9rng = np.random.RandomState(42)
10
11# Generating training data
12X_train = 0.2 * rng.randn(1000, 2)
13X_train = np.r_[X_train + 3, X_train]
14X_train = pd.DataFrame(X_train, columns = ['x1', 'x2'])
15
16# Generating new, 'normal' observation
17X_test = 0.2 * rng.randn(200, 2)
18X_test = np.r_[X_test + 3, X_test]
19X_test = pd.DataFrame(X_test, columns = ['x1', 'x2'])
20
21# Generating outliers
22X_outliers = rng.uniform(low=-1, high=5, size=(50, 2))
23X_outliers = pd.DataFrame(X_outliers, columns = ['x1', 'x2'])همانطور که مشاهده میکنید دادههای آموزشی و آزمایشی دو بعدی بوده و اولی شامل ۱۰۰۰ و دومی شامل ۲۰۰ مشاهده هستند. همچنین برای تولید نقاط ناهنجار نیز از توزیع یکنواخت در بازه ۱- تا ۵ استفاده شده است.

اکنون باید کار آموزش الگوریتم جنگل ایزوله در پایتون را انجام دهیم. در اینجا از تنظیمات پیش فرض کتابخانه scikit-learn به این منظور استفاده میکنیم. نکته قابل ذکر این است که پارامتر آلودگی، که درصد مشاهدات نامتعارف را نشان میدهد باید به الگوریتم معرفی کنیم (0.1 مقدار پیش فرض در کتابخانه scikit-learn است).
1# Isolation Forest ----
2
3# training the model
4clf = IsolationForest(max_samples=100, random_state=rng)
5clf.fit(X_train)
6
7# predictions
8y_pred_train = clf.predict(X_train)
9y_pred_test = clf.predict(X_test)
10y_pred_outliers = clf.predict(X_outliers)در گام بعدی میخواهیم به کمک کدهای زیر، دقت و کارایی الگوریتم را اندازهگیری کنیم. در قسمتی از کد بالا مشاهده کردید که برای دادههای آزمایشی و آموزشی، مقدار پیشبینی شده (Prediction) محاسبه شده است.
میدانیم که مجموعه دادههای آزمایشی فقط شامل مشاهدات مربوط به توزیع نرمال و مشاهدات عادی است. بنابراین، تمام مشاهدات مجموعه آزمایشی باید توسط الگوریتم نیز به عنوان مشاهدات هنجار شناسایی شوند. همچنین در بخش دادههای ناهنجار (با رنگ قرمز) که به مشاهدات آزمایشی اضافه شدهاند، باید دقت را محاسبه کنیم. واضح است که تعداد این مشاهدات از قبل مشخص شده است و میدانیم که تعدادشان ۵۰ مورد است.
با استفاده از کد زیر میزان دقت (نسبت تعداد مشاهدات هنجار نسبت به نقاط پیشبینی شده) برای دو حالت (بدون مشاهدات ناهنجار و با مشاهدات ناهنجار) محاسبه شده است.
1# new, 'normal' observations ----
2print("Accuracy:", list(y_pred_test).count(1)/y_pred_test.shape[0])
3# Accuracy: 0.93
4# outliers ----
5print("Accuracy:", list(y_pred_outliers).count(-1)/y_pred_outliers.shape[0])
6# Accuracy: 0.96همانطور که مشخص است در حالتی که هیچ مشاهده ناهنجاری در مجموعه دادههای آزمایشی وجود ندارد، دقت عملکرد الگوریتم ۹۳ درصد (0٫93) است. زمانی که دادههای ناهنجار به الگوریتم معرفی شدهاند، با دقت ۹6 درصد (۰٫۹6) به درستی آنها را تشخیص داده است.
در ابتدا، این نتایج به خصوص با توجه به تنظیمات پیش فرض بسیار خوب به نظر میرسد، با این حال، یک مسئله هنوز هم باید مورد توجه قرار گیرد. از آنجا که دادههای ناهنجار به طور تصادفی تولید میشوند، برخی از مناطق مربوط به مشاهدات نامتعارف در واقع در بین مشاهدات عادی قرار دارند. برای بازرسی دقیقتر، مجموعه دادههای مشاهده نامتعارف را با یک برچسب مشخص و جداگانه، نمایش خواهیم داد. به این ترتیب میتوانیم ببینیم که برخی از نقاط ناهنجار در داخل مجموعههای نقاط متعارف قرار گرفته و توسط الگوریتم جنگل ایزوله در پایتون به صورت نقاط هنجار شناسایی شدهاند.
کاری که میتوانیم انجام دهیم این است که مشخصات پارامترهای مختلف (میزان تداخل، تعداد برآوردگرها، تعداد نمونه برای ترسیم برآوردگرهای اصلی و غیره) را ترسیم یا تغییر دهیم تا مشخص شود که باز هم چنین نقاطی به صورت عادلی و هنجار تلقی میشوند یا خیر. ولی به هر حال نتایج حاصل تا اینجا رضایت بخش بوده است.
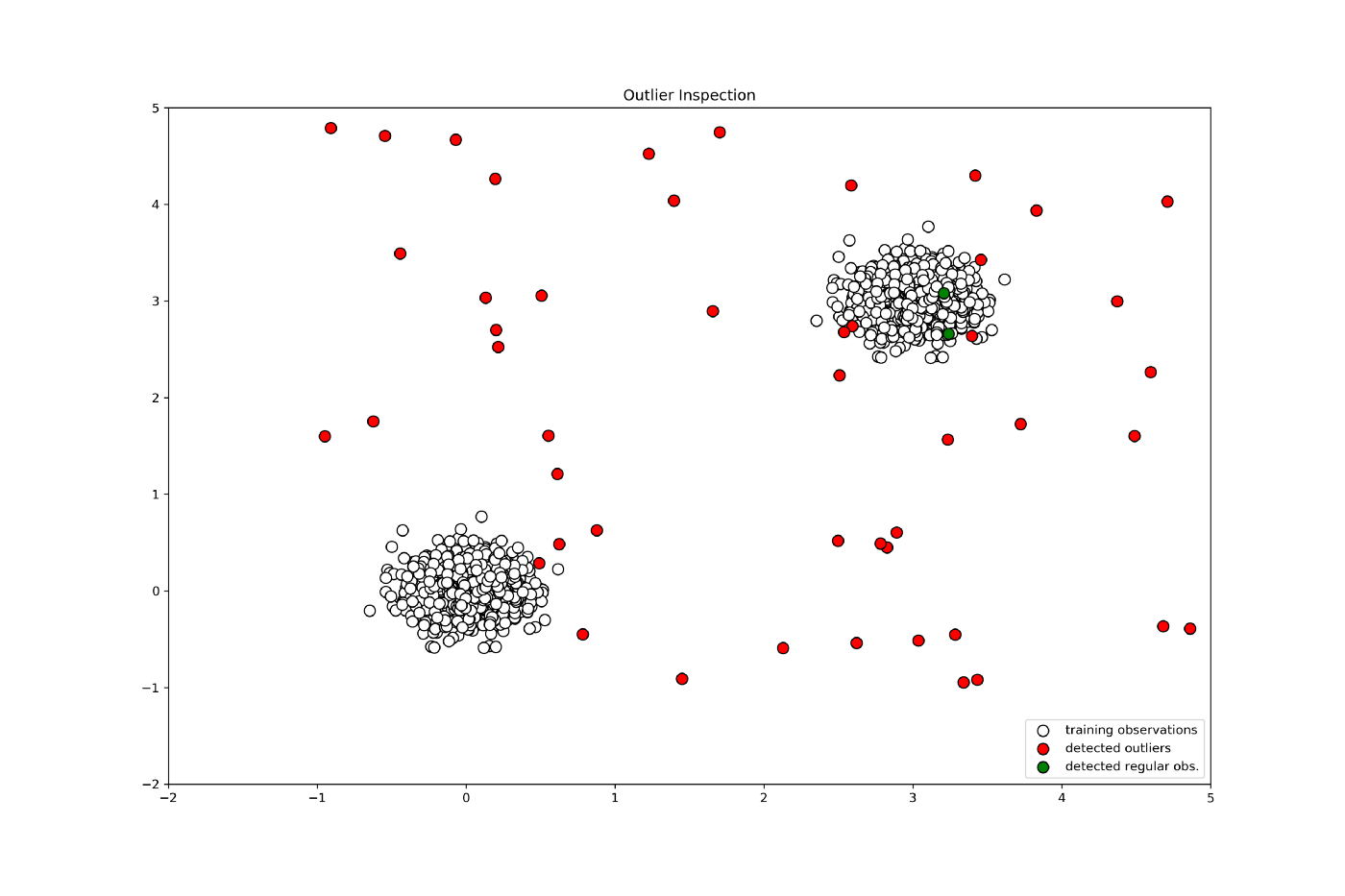
همانطور که در تصویر ۳، مشاهده میکنید، نقطههای سبز رنگ نشانگر مشاهدات ناهنجاری هستند که به صورت متعارف شناسایی شدهاند. همچنین نقطههای سفید رنگ، مشاهدات آزمایشی و نقطههای قرمز رنگ، ناهنجاریهای شناسایی شده هستند.
خلاصه و جمعبندی
جنگل ایزوله یا جنگل جداسازی یک الگوریتم یا تکنیک تشخیص فاصله است که به جای مشاهدات عادی بر ناهنجاریها تکیه دارد که درست به مانند روشی که در جستجوی درخت باینری عمل میشود، وظیفه شناسایی نقاط یا مشاهدات ناهنجار را انجام میدهد.
در این نوشتار الگوریتم جنگل ایزوله در پایتون پیاده سازی شده و کارایی و قابلیتهای آن نیز به کمک مثالهایی معرفی و مشخص شد. در بیشتر الگوریتمها موجود در این زمینه، ویژگیهای دادههای متعارف مشخص شده، سپس مقادیر ناهنجار براساس دوری از نقاط متعارف تعیین میشوند در حالیکه مطابق با الگوی الگوریتم جنگل ایزوله، از همان ابتدا، نقاط ناهنجار بدون استفاده از توابع فاصله، مشخص و از مجموعه دادههای اصلی جدا میشوند. همین امر نقطه قوت این الگوریتم در شناسایی نقطهها یا مشاهدات ناهنجار یا دورافتاده محسوب میشود.












