نامساوی کانتلی و باتاچاریا — به زبان ساده

در نوشتارهای دیگر مجله فرادرس با نامساوی‌های احتمال نظیر نامساوی مارکف (Markov Inequality) و نامساوی چبیشف (Chebyshev Inequality) آشنا شدید. در این نوشتار به بررسی نامساوی کانتلی و باتاچاریا خواهیم پرداخت که با توجه به مقدار پارامتر آن، یک کران بالا یا پایین برای احتمال تجمعی یا تابع بقا متغیر تصادفی ایجاد می‌کند.

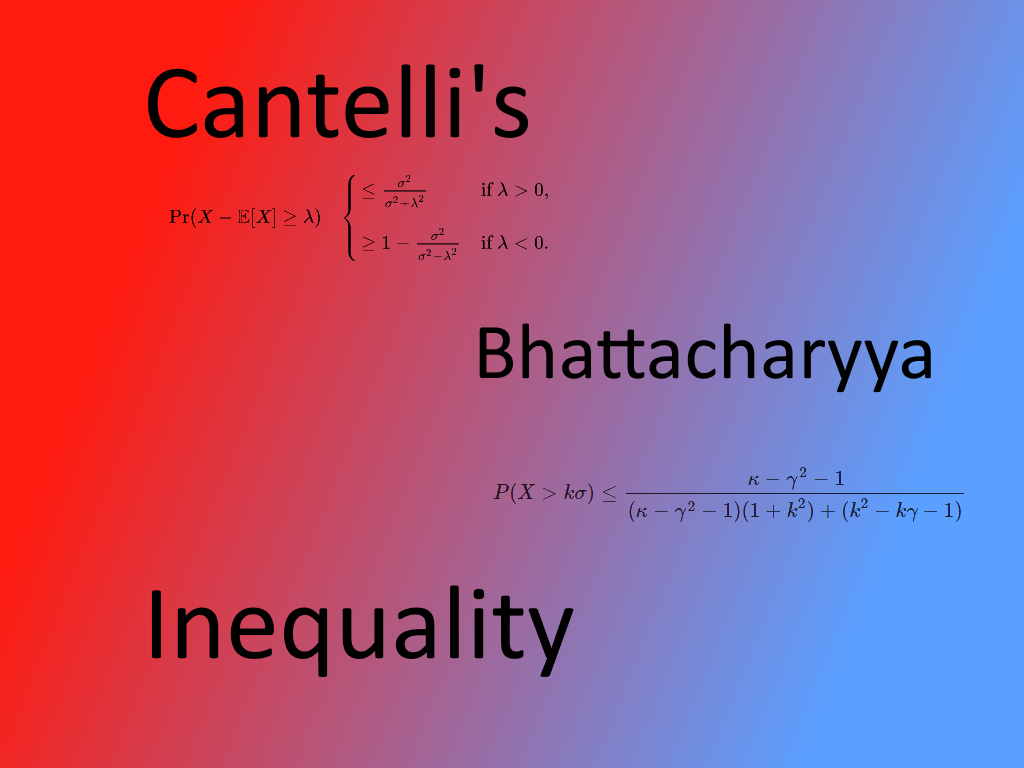
برای درک و آشنایی با اصطلاحات به کار رفته در این نوشتار بهتر است مطالب متغیر تصادفی، تابع احتمال و تابع توزیع احتمال و امید ریاضی (Mathematical Expectation) — مفاهیم و کاربردها را مطالعه کنید. همچنین خواندن نوشتار توزیع تجمعی — به زبان ساده نیز خالی از لطف نیست.

نامساوی کانتلی و باتاچاریا

فرض کنید متغیر تصادفی $$X$$ با تابع احتمال $$\Pr$$ مشخص شده است. امید ریاضی و واریانس این متغیر تصادفی نیز متناهی و مشخص بوده و به ترتیب با نمادهای $$\operatorname{E}(X)$$ و $$\sigma^2$$ نشان داده می‌شود. نامساوی مارکف و چبیشف به منظور پیدا کردن کران بالا برای تابع احتمال (تابع بقاء) متغیر تصادفی به کار می‌روند. البته نامساوی کانتلی و باتاچاریا نسبت به دو نامساوی قبلی بهتر عمل کرده و برای کران بالای احتمال، مقادیر تیزتری دارند.

فیلم آموزش تئوری احتمالات در فرادرس

کلیک کنید

نامساوی کانتلی (Cantelli's Inequality)، حالت عمومی‌تری برای نامساوی چبیشف را ارائه می‌کند. به همین علت برای یادآوری ابتدا نامساوی چبیشف را در نظر می‌گیریم.

نامساوی چبیشف: متغیر تصادفی $$X$$ با شرایط بالا را در نظر بگیرید. در این صورت برای هر $$k>0$$ خواهیم داشت:

$$ \large \Pr(|X-\mu | \geq k \sigma ) \leq { \frac {1}{k^{2}}} $$

همانطور که مشاهده می‌کنید این نامساوی برای قدر مطلق فاصله متغیر تصادفی از میانگین و همچنین مقادیر مثبت $$k$$ نوشته شده است. ولی در نامساوی کانتلی این محدودیت‌ها برداشته شده است.

این نامساوی به افتخار «فرانچسکو کانتلی» (Francesco Paolo Cantelli) که در سال ۱۹۲۸ این نامساوی را معرفی کرد، نام‌گذاری شده است. او ایده و محاسبات خود را براساس نامساوی چبیشف بنا نهاد.

نامساوی چبیشف بیان می‌کند که احتمال فاصله متغیر تصادفی از میانگین آن (قدر مطلق فاصله) چه رابطه‌ای با مضارب واریانس آن متغیر تصادفی دارد. در حالیکه در نامساوی کانتلی (که گاهی آن را نامساوی چبیشف-کانتلی هم می‌نامند) احتمال بزرگتر یا کوچکتر بودن متغیر تصادفی از میانگینش محاسبه می‌شود.

نامساوی کانتلی و اثبات آن

صورت نامساوی کانتلی به شکل زیر است:

$$ \large {\displaystyle \Pr(X-\mathbb {E} [X]\geq \lambda )\quad {\begin{cases}\leq {\frac {\sigma ^{2}}{\sigma ^{2} + \lambda^{2}}}&{\text{if }}\lambda >0 ,\\[8pt] \geq 1-{\frac {\sigma ^{2}}{\sigma ^{2} + \lambda ^{2}}} & {\text{if }}\lambda  < 0 \end{cases}}} $$

رابطه ۱

که در آن $$X$$ متغیر تصادفی با اندازه احتمال $$ \Pr $$ و امید ریاضی $$ \operatorname{E} [X] $$ و واریانس $$ \sigma^2 $$ است.

البته می‌توان با ترکیب دو حالت $$\lambda>0$$ با $$\lambda<0$$ از رابطه ۱ به رابطه زیر رسید.

$$ \large {\displaystyle \Pr( |X-\mathbb {E} [X] | \geq \delta ) \leq { \frac { 2 \sigma ^{2}}{ \sigma^{2} + \delta^{2}}}} $$

رابطه ۲

نکته: فرض بر این است که واریانس متغیر تصادفی $$X$$ از صفر بزرگتر است. یعنی داریم $$\sigma^2 \neq 0$$.

اثبات

دو حالت $$\lambda>0$$ و $$\lambda<0$$ را بطور جداگانه در نظر می‌گیریم. در نتیجه اثبات را به دو بخش تقسیم می‌کنیم. ابتدا متغیر تصادفی $$Y=X-\operatorname{E}[X]$$ را در نظر بگیرید. واضح است که در این حالت داریم:

$$ \large {\displaystyle \mathbb {E} [Y] = 0}, \; \; {\displaystyle \operatorname {Var} (Y) = \sigma ^{2}}$$

حالت $$\lambda>0$$

برای هر $$u\geq 0$$ می‌توان نوشت:

$$\large { \displaystyle \Pr(X - \mathbb {E} [X] \geq \lambda ) = \Pr(Y \geq \lambda ) = \Pr(Y + u \geq \lambda + u ) \leq \Pr((Y + u)^{2}}$$

بوسیله نامساوی مارکف رابطه بالا را به صورت نامساوی می‌نویسیم.

$$ \large {\Pr(Y + u \geq \lambda + u) \leq \Pr((Y + u)^{2} \geq (\lambda + u)^{2})\leq {\frac {\mathbb {E} [(Y + u)^{2}]}{(\lambda + u)^{2}}} = {\frac {\sigma ^{2} + u^{2}}{(\lambda + u)^{2}}}} $$

رابطه ۳

از آنجایی که نامساوی بالا به ازاء همه مقادیر $$u\geq 0$$ برقرار است، مقداری از $$u$$ را پیدا می‌کنیم که طرف راست نامساوی را کمینه کند.

با مشتق‌گیری از طرف راست نامساوی برحسب $$u$$ داریم:

$$ \large \dfrac{ \partial \left( \frac{ \sigma ^{2} + u^{2}}{(\lambda + u)^{2}}\right)}{ \partial u} = 0 $$

پس

$$ \large \dfrac{ 2 u (\lambda + u)^2 - 2(\lambda + u)( \sigma^2 + u^2)}{(\lambda + u)^4} = \dfrac{2u( \lambda + u) - 2( \sigma^2 + u^2)}{(\lambda + u)^ 3} = 0 $$

که با صفر قرار دادن صورت خواهیم داشت:

$$ \large u ( \lambda + u) - ( \sigma^2 + u^2) = u \lambda + u^2 - \sigma^2 - u^2 = u \lambda - \sigma^2 = 0 \rightarrow u_{ \ast } = \frac{ \sigma^2}{ \lambda} $$

پس $$u_{\ast }$$ مقداری است که رابطه ۱ را کمینه می‌سازد پس $$u_{\ast }$$ را در آن قرار می‌دهیم.

$$ \large {\displaystyle \Pr( X- \mathbb {E} [X] \geq \lambda ) \leq { \frac { \sigma ^{2} + u_{ \ast }^{2}}{( \lambda + u_{ \ast })^{2}}}={ \frac { \sigma ^{2}}{\lambda ^{2}+ \sigma ^{2}}}} $$

رابطه ۴

به این ترتیب حکم یعنی نامساوی کانتلی ثابت می‌شود.

حالت $$\lambda<0$$

در این حالت $$ \alpha\; =\; - \;\lambda > 0 $$ در نظر گرفته شده و برای $$ u \geq 0 $$ می‌نویسیم:

$$ \large {\displaystyle \Pr(X- \mathbb {E} [X] < \lambda )= \Pr(-Y>\alpha ) \leq { \frac { \sigma ^{2}}{ \alpha ^{2}+\sigma ^{2}}}={ \frac { \sigma ^{2}}{ \lambda ^{2}+ \sigma ^{2}}}} $$

رابطه ۵

مشخص است که با در نظر گرفتن $$\alpha>0$$ به کمک نامساوی مربوط به رابطه ۴، نامساوی رابطه ۵ نوشته شده است. با در نظر گرفتن متمم پیشامد $$ X-\operatorname{E}[X] < \lambda $$ (طرف چپ نامساوی رابطه ۵) می‌توان نوشت:

$$ \large { \displaystyle \Pr (X- \mathbb {E} [X] \geq \lambda ) \geq { \frac { \lambda ^{2}}{ \lambda ^{2}+ \sigma ^{2}}}} $$

به این ترتیب نامساوی کانتلی برای هر دو حالت، اثبات شد.

کاربرد نامساوی کانتلی

یکی از نکات جالبی که از نامساوی کانتلی می‌توان نتیجه گرفت فاصله بین میانگین و میانه یک توزیع است. نامساوی کانتلی نشان می‌دهد که فاصله بین میانگین و میانه در هر توزیع، هرگز از یک انحراف معیار بزرگتر نخواهد بود.

برای روشن‌تر شدن موضوع متغیر تصادفی $$X$$ با میانگین $$\mu$$ و میانه $$\nu$$ و انحراف معیار $$\sigma$$ را در نظر بگیرید. باید نشان دهیم که رابطه زیر برای این سه پارامتر برای هر متغیر تصادفی، برقرار است.

$$ \large | \mu - \nu | \leq \sigma $$

برای اثبات این قضیه، فرض می‌کنیم که در نامساوی کانتلی $$ \lambda = \sigma $$ باشد.

نکته: اگر $$\sigma$$ نامتناهی باشد که قضیه به راحتی اثبات می‌شود. پس فرض می‌کنیم که انحراف معیار متناهی است.

برای شروع، نامساوی کانتلی را به صورت زیر بازنویسی می‌کنیم.

$$ \large \Pr(X- \mu \geq \sigma ) \leq { \frac {1}{2}} \implies \Pr (X \geq \mu + \sigma ) \leq { \frac {1}{2}} $$

حال، علامت متغیر تصادفی $$X$$ را تغییر می‌دهیم. واضح است که میانگین آن هم تغییر علامت خواهد داد، زیرا $$ \operatorname{E} [aX]=a \operatorname{E}(X)$$. پس خواهیم داشت:

$$\large \Pr(X \leq \mu - \sigma )\leq { \frac {1}{2}} $$

از طرفی با توجه به مفهوم میانه متغیر تصادفی، می‌توانیم نامساوی‌های زیر را برای $$ \nu $$ بنویسیم:

$$ \large {\displaystyle \operatorname {P} (X\leq \nu) \geq { \frac {1}{2}}} $$

$$ \large \operatorname {P} (X \geq \nu) \geq { \frac {1}{2}} $$

پس نتیجه خواهیم گرفت، تعداد نقاطی که یک انحراف معیار از میانگین فاصله دارند از تعداد نقطه‌هایی که از میانه کوچکترند، کمتر هستند. در نتیجه:

$$ \large  | \mu  -\sigma | \leq  \nu \; \rightarrow \; -\nu \leq \mu - \sigma \leq \nu  \; \; \rightarrow  \; \; |\mu - \nu | \leq \sigma$$

در نوشتارهای قبلی در مورد نامساوی‌های آماری، مقایسه‌ای بین مقدار واقعی احتمال و کران بالای آن با استفاده از زبان برنامه‌نویسی برای توزیع‌های دوجمله‌ای و نرمال ارائه کردیم. این کار را هم برای نامساوی کانتلی در ادامه تکرار خواهیم کرد.

مقایسه نامساوی کانتلی برای توزیع دو جمله‌ای

فرض کنید متغیر تصادفی دو جمله‌ای (Binomial Distribution) با پارامترهای n=15 و p=۰٫5 داریم. به ازاء مقادیر مختلف $$\lambda$$ نمودار مربوط به احتمال و کران‌های بالای نامساوی‌های کانتلی را رسم می‌کنیم. کد زیر به این منظور نوشته شده است.

1n=15
2lambda =seq(0,n,1)
3p=0.5
4mu=n*p
5sigma2=mu*(1-p)
6px=pbinom(lambda+mu,n,p,lower.tail=TRUE)
7cantellibound=sigma2/(sigma2+lambda^2)
8
9plot(lambda,px,xlab="lambda",ylab="Pr",ylim=c(0,15),col="red",lty=1,type="l")
10lines(lambda,cantellibound,col="blue",lty=2)
11legend(8,15,legend=c("P(X-mu>lambda)","Cantelli"),col=c("red","blue"),lty=1:2,cex=1)

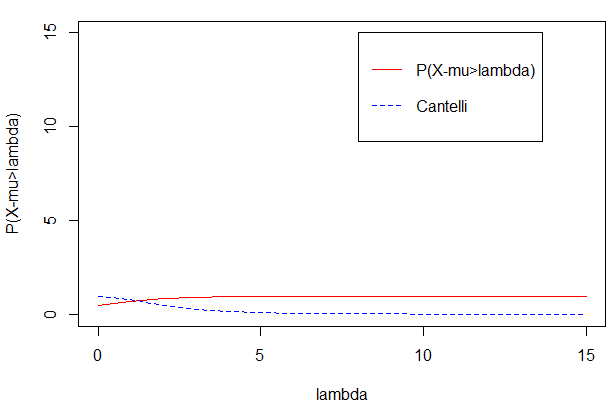
حاصل اجرای این برنامه، نموداری است که در تصویر زیر دیده می‌شود. همانطور که مشخص است نامساوی کانتلی بسیار به مقدار واقعی احتمال نزدیک است.

مقایسه نامساوی کانتلی برای توزیع نرمال

متغیر تصادفی با توزیع نرمال با پارامترهای میانگین $$\mu = 0$$ و واریانس $$s\sigma^2=1$$ را در نظر بگیرید. به ازاء مقادیر مختلف $$\lambda$$ به کمک برنامه و کدهای زیر، نمودار مربوط به احتمال و کران‌های بالای نامساوی‌های کانتلی را رسم می‌کنیم.

1mu=0
2sigma2 =1
3lambda=seq(0,10,0.01)
4px=1-pnorm(lambda*sigma+mu,mu,sigma)
5cantellibound=sigma2/(sigma2+lambda^2)
6
7plot(lambda,px,xlab="lambda",ylab="P(X-mu>lambda)",ylim=c(0,10),col="red",lty=1,type="l")
8lines(lambda,cantellibound,col="blue",lty=2)
9legend(6,10,legend=c("P(X-mu>lambda)","Cantelli"),col=c("red","blue"),lty=1:2,cex=1)

نتیجه اجرای این برنامه توسط یک نمودار مطابق با تصویر زیر دیده می‌شود. باز هم مشخص است که طرف راست نامساوی کانتلی به مقدار واقعی احتمال بسیار نزدیک است.

نامساوی باتاچاریا (Bhattacharyya Inequality)

یک نامساوی دیگر که به صورت تعمیم یافته نامساوی کانتلی است، نامساوی باتاچاریا (Bhattacharyya Inequality) نام دارد که در سال ۱۹۸۷ طی مقاله‌ای برای تعمیم نامساوی چبیشف و کانتلی توسط دانشمند هندی «برید باران باتاچاریا» (Barid Baran Bhattacharya) معرفی شد.

فیلم آموزش تحلیل داده ها با نرم افزار مینی تب Minitab – مقدماتی در فرادرس

کلیک کنید

در این نامساوی از گشتاورهای مرتبه سوم و چهارم متغیر تصادفی $$X$$ استفاده می‌شود.

فرض کنید که $$\text{E}[X]=0$$ و واریانس $$\sigma^2$$ هم مثبت باشد. در این صورت اگر $$ \gamma = \frac{\text{E}[X^3]} { \sigma^3} $$ و $$ \kappa = \frac{\text{E}[X^4]}{ \sigma^4} $$ باشد، آنگاه برای تابع احتمال متغیر تصادفی $$X$$ خواهیم داشت:

$$ \large P(X>k \sigma ) \leq { \frac { \kappa - \gamma ^{2}-1}{( \kappa - \gamma ^{2}-1)(1+k^{2})+(k^{2}-k \gamma -1)}} $$

به شرطی که $$\kappa^2-\kappa\gamma-1>0$$ باشد. البته اگر مقدار $$\kappa$$ به حد کافی بزرگ باشد، رابطه قبل محقق خواهد شد.

نکته: گشتاور سوم و چهارم در اینجا به مانند میزان چولگی (Skewness) و کشیدگی (Kurtosis) توزیع متغیر تصادفی $$X$$ عمل می‌کنند. در نتیجه زمانی نامساوی باتاچاریا موثر است که میزان کشیدگی متغیر تصادفی زیاد باشد.

خلاصه و جمع‌بندی

در این نوشتار به بررسی و مقایسه نامساوی‌ها کانتلی و باتاچاریا پرداختیم. همچنین اثبات نامساوی کانتلی را در دو حالت مرور کردیم. هر چند این نامساوی‌ها نسبت به نامساوی چبیشف و مارکف، تیز تر هستند ولی به علت سهولت، نامساوی مارکف و چبیشف بیشتر به کار می‌روند.

در صورت علاقه‌مندی به مباحث مرتبط در زمینه ریاضی و آمار، آموزش‌های زیر نیز به شما پیشنهاد می‌شوند:

• مجموعه آموزش‌های آمار و احتمالات
• آموزش آمار و احتمال مهندسی
• مجموعه آموزش‌های ریاضیات
• توزیع‌های آماری — مجموعه مقالات جامع وبلاگ فرادرس
• متغیر تصادفی و توزیع برنولی — به زبان ساده
• توزیع نرمال یک و چند متغیره — مفاهیم و کاربردها

^^