نامساوی چبیشف و اثبات آن — از صفر تا صد

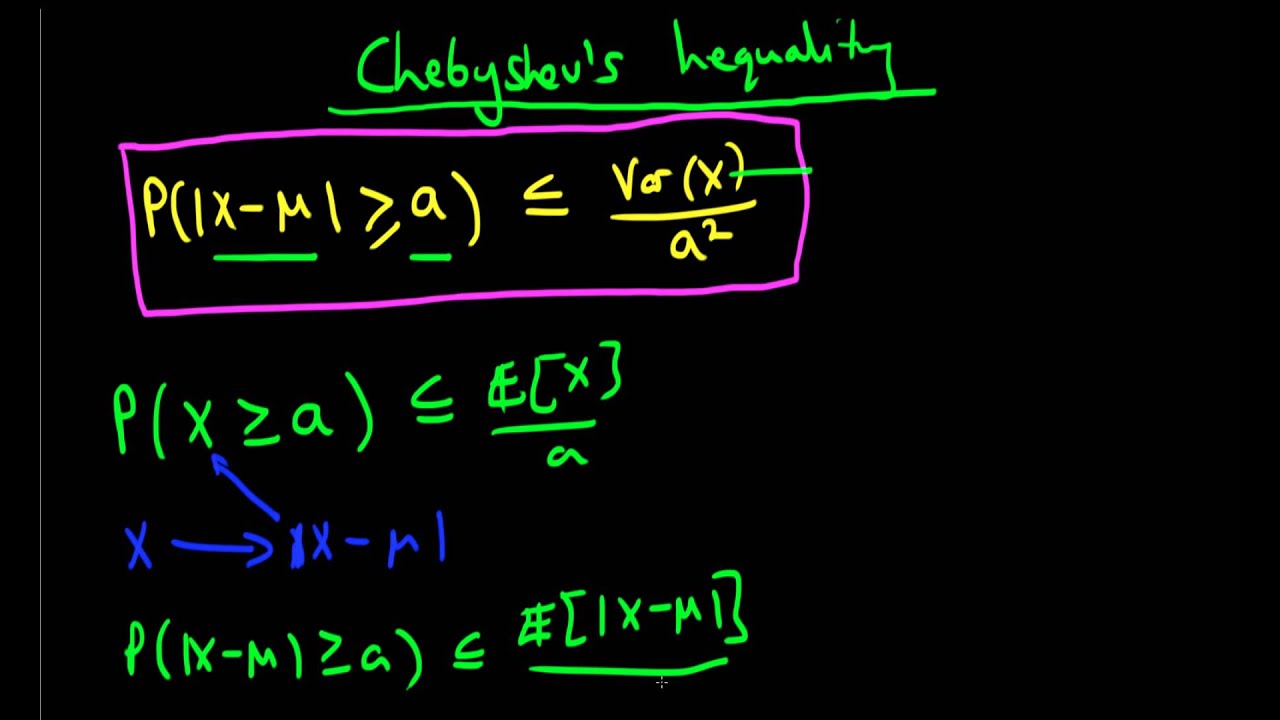
در نظریه احتمال، از نامساوی‌هایی زیادی برای نشان دادن رابطه بین احتمالات و تعیین کران‌های آن‌ها استفاده می‌شود. در این بین نامساوی چبیشف (Chebeshev Inequality) نقش مهمی در تعیین کران بالا برای احتمال یا تابع توزیع احتمال تجمعی یک متغیر تصادفی ایفا می‌کند.

در نامساوی چبیشف، کران بالا بوسیله میانگین و واریانس متغیر تصادفی تعیین می‌شود. دیگر نامساوی‌های احتمالاتی مانند نامساوی مارکف (Markov inequality) و نامساوی هولدر (Holder Inequality) نیز برای محاسبه کران‌های تابع توزیع تجمعی یا امید ریاضی به کار می‌روند. در این نوشتار به نامساوی چبیشف و اثبات آن خواهیم پرداخت و با ذکر مثال‌هایی اهمیت استفاده از آن را مرور خواهیم کرد.

برای آشنایی با اصطلاحات به کار رفته در این نوشتار بهتر است مطالب امید ریاضی (Mathematical Expectation) — مفاهیم و کاربردها و متغیر تصادفی، تابع احتمال و تابع توزیع احتمال را بخوانید. همچنین خواندن نامساوی چبیشف – کاربرد در توزیع‌های غیرنرمال (+) نیز خالی از لطف نیست.

نامساوی چبیشف و اثبات آن

نامساوی چبیشف براساس نام ابداع کننده آن یعنی «پافنوتی لوویچ چبیشف» (Pafnuty Lvovich Chebyshev) اسم گذاری شده است. این ریاضی‌دان روس، در سال 1867 نامساوی دوست و همکارش «ژول بینایمه» (Jules Bienayme) را که در سال 1853 معرفی شده بود، اثبات کرد.

فیلم آموزش تئوری احتمالات در فرادرس

کلیک کنید

البته بعدها، این نامساوی توسط مارکف که از شاگردان چبیشف بود، به شکل دیگری اثبات شد.

معمولا قضیه چبیشف به دو صورت یا شیوه بیان می‌شود، یک روش به صورت احتمالاتی (Probabilistic Statement) است و روش دیگر به کمک نظریه اندازه (Measure Theory) نامساوی چبیشف را مشخص می‌کند. در ادامه هر دو شیوه، ارائه شده و اثبات آن‌ها نیز مطرح می‌شود. منظور از شیوه نظریه اندازه در نامساوی چبیشف آن است که اگر فضای احتمال را به فضای اندازه‌پذیر (Measurable Space) گسترش دهیم، باز هم قضیه چبیشف صادق خواهد بود.

قضیه نامساوی چبیشف با بیان احتمالاتی

فرض کنید متغیر تصادفی $$X$$ دارای امید ریاضی ($$\mu$$) و واریانس متناهی ($$\sigma^2\neq0$$) باشد. در این صورت برای هر $$k>0$$ خواهیم داشت:

$$\large \Pr(|X-\mu |\geq k\sigma )\leq {\frac {1}{k^{2}}}$$

رابطه ۱

برای مثال فرض کنید که $$k = \sqrt{2}$$ در نتیجه می‌توان طبق نامساوی چبیشف گفت که احتمال اینکه مقداری از متغیر تصادفی خارج از بازه $$(\mu-\sqrt{2}\sigma , \mu+\sqrt{2}\sigma)$$ قرار گیرد از ۰٫۵ کمتر است.

نکته: در این قضیه مقدارهایی از $$k$$ مورد نظر است که از ۱ بزرگتر باشند زیرا برای مقدارهای $$k\leq 1$$ این نامساوی امری بدیهی در احتمال محسوب می‌شود. زیرا مقدار احتمال برای هر پیشامد (یا متغیر تصادفی) کوچکتر یا مساوی با ۱ است. واضح است که برای مقادیر $$k<1$$ نسبت $$\frac{1}{k^2}$$‌ از یک بزرگتر خواهد بود.

جدول زیر براساس مقادیر مختلف $$k$$ شکل گرفته است که احتمال قرارگیری فاصله مقداری از میانگین را برحسب ضرایبی از $$\sigma$$ نشان می‌دهد.

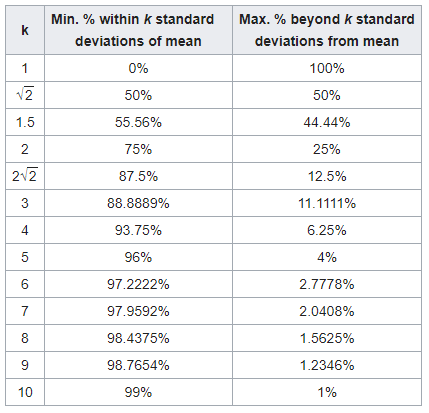
مقدار کران بالا (نامساوی چبیشف) و کران پایین (عکس نامساوی چبیشف) نیز دیده می‌شود. به این ترتیب ستون اول شامل مقادیر مختلف $$k$$ است و ستون دوم نیز $$\Pr(|X-\mu|\leq k\sigma)$$ (عکس نامساوی چبیشف) و ستون سوم نیز احتمال $$\Pr(|X-\mu|\geq k\sigma)$$ (نامساوی چبیشف) را نشان می‌دهد.

همانطور که مشاهده می‌کنید، احتمال اینکه مشاهده‌ای دارای فاصله‌ای بزرگتر از 5 انحراف معیار از میانگین باشد، حداکثر ۴٪ است و تقریبا در اکثر موارد، فاصله متغیر تصادفی از میانگین آن، کمتر از ۱۰ برابر انحراف‌معیار است. در جدول این احتمال با مقدار 99٪ مشخص شده است.

مثال

فرض کنید مقاله‌ای علمی را در یک مجله‌ به تصادف انتخاب کرده‌ایم. همچنین در نظر بگیرید که به طور متوسط در هر مقاله از این مجله علمی، ۱۰۰۰ کلمه و با واریانس ۲۰۰ کلمه وجود دارد. به این ترتیب می‌توان احتمال اینکه مقاله انتخابی کمتر از ۶۰۰ یا بیش از ۱۴۰۰ کلمه باشد را کمتر از ۰٫25 در نظر گرفت. مشخص است که در نامساوی چبیشف $$k=2$$ بوده و در نتیجه $$\frac{1}{k^2}=\frac{1}{4}$$ محسوب شده است.

ولی توجه داشته باشید که اگر بدانیم توزیع کلمه‌ها، از توزیع نرمال با میانگین ۱۰۰۰ و واریانس ۴۰،۰۰۰ باشد، آنگاه مقدار این احتمال برابر است با:

$$\large \Pr(|X-1000 |\geq 2 \times 200)=1- \Pr(-400\leq X-1000\leq 400)=\\ \large 1-\Pr(600\leq X\leq 1400) =1-0.95=0.05 $$

با مقایسه با کران حاصل از نامساوی چبیشف، مشخص است که این نامساوی، کران دقیقی ارائه نمی‌کند و بخصوص در زمانی که اطلاعاتی در مورد توزیع متغیر تصادفی داریم، فاصله زیادی بین کران بالا چبیشف و مقدار واقعی احتمال وجود دارد. البته همیشه مقدار این احتمال از کران چبیشف کوچکتر است. در ادامه به نمودارهایی خواهیم پرداخت که این امر را به خوبی نشان می‌دهند.

قضیه نامساوی چبیشف با نظریه اندازه

فضای اندازه $$(X,\Sigma, \mu)$$ را در نظر بگیرید.‌ فرض کنید تابع $$f$$ تابعی با مقادیر حقیقی توسعه یافته (شامل بی‌نهایت منفی و مثبت) باشد که روی $$X$$ اندازه‌پذیر $$\mu$$ است. آنگاه برای $$t>0$$ و $$0<p<\infty$$ خواهیم داشت:

$$\large {\displaystyle \mu (\{x\in X\,:\,\,|f(x)|\geq t\})\leq {1 \over t^{p}}\int _{|f|\geq t}|f|^{p}\,d\mu} $$

رابطه ۲

حتی به طور کلی می‌توان رابطه بالا را برای تابع یکنوای صعودی و نامنفی $$g$$ روی برد (Range) تابع $$f$$ نیز نوشت:

$$\large \mu (\{x\in X\,:\,\,f(x)\geq t\})\leq {1 \over g(t)}\int _{X}g\circ f\,d\mu . $$

رابطه ۳

توجه داشته باشید که اگر در رابطه ۳ تابع به صورت $$g(x)=|x|^p$$ باشد همان رابطه ۲ بدست می‌آید، به شرطی که $$x\geq t$$ باشد.

نکته: در اینجا منظور از $$g \circ f$$ ترکیب دو تابع $$f$$ و $$g$$ است.

اثبات نامساوی چبیشف با بیان احتمالاتی

برای نامساوی چبیشف با بیان احتمالاتی، اثبات‌های مختلفی وجود دارد. برای مثال می‌توان از نامساوی مارکف برای اثبات نامساوی چبیشف استفاده کرد. همچنین با در نظر گرفتن متغیر نشانگر نیز این نامساوی را می‌توان اثبات کرد. حتی یک روش اثبات براساس متغیر تصادفی پیوسته نیز وجود دارد. در ادامه اثبات این نامساوی را به هر سه روش توضیح خواهیم داد.

فیلم آموزش آمار و احتمال مهندسی در فرادرس

کلیک کنید

اثبات بر اساس نامساوی مارکف

نامساوی مارکف برای متغیر تصادفی نامنفی $$Y$$ به صورت زیر نوشته می‌شود.

$$\large {\displaystyle \operatorname {P} (Y\geq a)\leq {\frac {\operatorname {E} (Y)}{a}},\;\;a>0} $$

حال متغیر تصادفی $$X$$ را به صورت زیر در نظر بگیرید.

$$\large X=(Y-\mu)^2$$

به این ترتیب اگر $$a=(k\sigma)^2$$ باشد، نامساوی چبیشف به کمک نامساوی مارکف، برای متغیر تصادفی $$X$$، اثبات می‌شود زیرا مشخص است که احتمالات زیر معادل هستند.

$$\large \Pr \left( (X-\mu)^2<c^2\right)=\Pr(|X-\mu|<c)$$

نکته: توجه دارید که در اینجا $$\mu$$ و $$\sigma$$ امید ریاضی و انحراف استاندار متغیر تصادفی $$X$$ هستند.

اثبات بر اساس متغیر نشانگر

پیشامد $$A$$ را در نظر بگیرید. متغیر تصادفی نشانگر $$I_A$$ را به صورت زیر تعریف می‌کنیم.

$$\large I_A=\begin{cases}1 & A\;\; \text{occurs}\\0 & A\;\; \text{not occurs}\end{cases}$$

به این معنی که اگر پیشامد $$A$$ رخ‌ دهد مقدار آن برابر با ۱ و در غیر اینصورت مقدار تابع نشانگر برابر با صفر خواهد بود. به این ترتیب طرف چپ نامساوی چبیشف را باز‌نویسی می‌کنیم.

$$\large {\displaystyle {\begin{aligned}\Pr(|X-\mu |\geq k\sigma )&=\operatorname {E} \left(I_{|X-\mu |\geq k\sigma }\right)\\ \large &=\operatorname {E} \left(I_{\left({\frac {X-\mu }{k\sigma }}\right)^{2}\geq 1}\right)\\\large &\leq \operatorname {E} \left(\left({X-\mu \over k\sigma }\right)^{2}\right)\\\large &={1 \over k^{2}}{\operatorname {E} ((X-\mu )^{2}) \over \sigma ^{2}}\\ \large &={1 \over k^{2}}\end{aligned}}}$$

همانطور که مشاهده می‌کنید، نامساوی به کار رفته در اثبات (سطر سوم) دارای دو ضعف عمده است که این امر باعث می‌شود کران نامساوی چبیشف از مقدار واقعی احتمال دور باشد و به اصطلاح، کران‌ تیزی (Sharp) ایجاد نکند. این دو ضعف در ادامه بررسی می‌شوند.

1. همانطور که در اثبات بالا مشاهده کردید اگر $${\displaystyle 0\leq \left({\frac {X-\mu }{k\sigma }}\right)^{2}<1}$$ باشد، در نامساوی به جای به کار بردن مقدار ۰ برای تابع نشانگر از مقدار $$ \left({\frac {X-\mu }{k\sigma }}\right)^{2}$$ استفاده شده است که مقداری مثبت است و باعث افزایش مقدار امید ریاضی می‌شود.
2. از طرفی اگر $$ {\displaystyle \left({\frac {X-\mu }{k\sigma }}\right)^{2}\geq 1}$$، باز هم به جای استفاده از مقدار ۱ برای تابع نشانگر، مقدار $$ {\displaystyle \left({\frac {X-\mu }{k\sigma }}\right)^{2}}$$ به کار رفته که بزرگتر یا مساوی با ۱ است.

به همین علت، کران ایجاد شده توسط نامساوی چبیشف بسیار بزرگ است.

اثبات برای متغیر تصادفی پیوسته

در این قسمت فرض می‌کنیم که متغیر تصادفی $$X$$، پیوسته و دارای تابع چگالی احتمال $$f(x)$$ و واریانس $$Var(X)$$ است. به این ترتیب مقدار احتمال آنکه متغیر تصادفی $$X$$ در بازه $$a$$ تا $$b$$ قرار گیرد به صورت زیر بدست می‌آید.

$$\large {\displaystyle {\begin{aligned}\Pr(a\leq X\leq b)=\int _{a}^{b}f_{X}(x)\,dx\end{aligned}}}$$

همینطور، واریانس این متغیر تصادفی نیز به شکل زیر قابل محاسبه است.

$$\large {\displaystyle {\begin{aligned}\operatorname {Var} (X)=\sigma ^{2}&=\int _{\mathbb {R} }(x-\mu )^{2}f(x)\,dx,\end{aligned}}}$$

به این ترتیب از سمت چپ نامساوی چبیشف، اثبات را آغاز می‌کنیم.

$$\large {\displaystyle {\begin{aligned}\Pr(|X-\mu |\geq k\sigma )&=\int _{|x-\mu |\geq k\sigma }f(x)\,dx\\ \large &\leq \int _{|x-\mu |\geq k\sigma }{\frac {|x-\mu |}{k\sigma }}f(x)\,dx\\ \large &\leq \int _{|x-\mu |\geq k\sigma }{\frac {(x-\mu )^{2}}{k^{2}\sigma ^{2}}}f(x)\,dx\\ \large &=\int _{|x-\mu |\geq k\sigma }{\frac {1}{k^{2}\sigma ^{2}}}(x-\mu )^{2}f(x)\,dx\\ \large &={\frac {1}{k^{2}\sigma ^{2}}}\int _{|x-\mu |\geq k\sigma }(x-\mu )^{2}f(x)\,dx\\&\leq {\frac {1}{k^{2}\sigma ^{2}}}\int _{-\infty }^{\infty }(x-\mu )^{2}f(x)\,dx\\&={\frac {1}{k^{2}\sigma ^{2}}}\sigma ^{2}\\ \large&={\frac {1}{k^{2}}}.\end{aligned}}}$$

به این ترتیب اثبات نامساوی چبیشف برای متغیر تصادفی پیوسته $$X$$ انجام می‌شود.

نکته: اگر در نامساوی چبیشف، $$k\sigma$$ را با $$\epsilon$$ جایگزین کنیم، رابطه زیر به دست خواهد آمد.

$$\large{\displaystyle {\begin{aligned}\Pr(|X-\mu |\geq \epsilon )\leq {\frac {\sigma ^{2}}{\epsilon ^{2}}}\end{aligned}}} $$

که بطور معادل به صورت زیر در می‌آید.

$$\large{\displaystyle {\begin{aligned}\Pr(|X-\mu |<\epsilon )>1-{\frac {\sigma ^{2}}{\epsilon ^{2}}}\end{aligned}}} $$

واضح است که بر این اساس، مقدار $$\epsilon$$ مثبت و حقیقی خواهد بود.

اثبات نامساوی چبیشف در نظریه اندازه

در مجموعه $$A_t$$ که به صورت $$ {\displaystyle A_{t}=\{x\in X\mid f(x)\geq t\}} $$ تعریف شده است، $$t$$ را ثابت در نظر بگیرید. همچنین تابع نشانگر $$1_{A_t}$$ را روی مجموعه $$A_t$$ تعریف می‌کنیم. واضح است که برای هر تابع غیرنزولی و مثبت روی برد $$f$$ مانند $$g(t)$$ رابطه زیر برقرار است.

$$\large 0\leq g(t)1_{A_{t}}\leq g(f(x))\,1_{A_{t}},\;\;\forall x$$

در نتیجه طبق آنالیز ریاضی و مفهوم انتگرال ریمان استیلتیس (Riemann Stieltjes) خواهیم داشت:

$$\large{\begin{aligned}g(t)\mu (A_{t})&=\int _{X}g(t)1_{A_{t}}\,d\mu \\ \large&\leq \int _{A_{t}}g\circ f\,d\mu \\\large &\leq \int _{X}g\circ f\,d\mu .\end{aligned}}$$

حال دو طرف این نامساوی را به تابع $$g(t)$$ که تابعی مثبت است، تقسیم می‌کنیم. در نتیجه جهت نامساوی تغییر نخواهد کرد.

$$\large\mu (\{x\in X\,:\,\,f(x)\geq t\})\leq {1 \over g(t)}\int _{X}g\circ f\,d\mu $$

نامساوی‌های دیگر بر مبنای نامساوی چبیشف

همانطور که دیدید، نامساوی چبیشف برمبنای احتمال دو طرفه و متقارن برحسب $$k$$ نوشته شده است. یعنی می‌توان آن را به صورت زیر درآورد.

$$\large\Pr(-k<\dfrac{X-\mu}{\sigma}<k)\geq 1-{\dfrac {1}{k^{2}}} $$

اگر بخواهیم نامساوی چبیشف را برای حالتی در نظر بگیریم که دو طرف نامساوی احتمال، قرینه نباشند باید به روش زیر محاسبات را انجام بدهیم.

فرض کنید تابع توزیع متغیر تصادفی $$X$$، نامعلوم بوده ولی مشخص باشد که متقارن است. برای مثال توزیع نرمال (Normal Distribution) یا توزیع کوشی (Cauchy Distribution) این وضعیت را دارند. به این معنی که $$f_X(x)=f_X(-x)$$. در این صورت می‌توانیم نامساوی دیگری بر مبنای نامساوی چبیشف ایجاد کنیم.

برای هر دو عدد $$k_1$$ و $$k_2$$ که بینشان رابطه $$k_1+k_2=0$$ برقرار باشد، داریم:

$$\large\Pr(k_{1}<X<k_{2})\geq 1-{\frac {4\sigma ^{2}}{(k_{2}-k_{1})^{2}}} $$

اگر توزیع احتمال نامتقارن یا نامعلوم باشد، برای $$k_1+k_2=2\mu$$ خواهیم داشت:

$$\large\Pr(k_{1}<X<k_{2})\geq {\frac {4[(\mu -k_{1})(k_{2}-\mu )-\sigma ^{2}]}{(k_{2}-k_{1})^{2}}} $$

واضح است که $$\mu$$‌ امید ریاضی و $$\sigma$$ نیز انحراف معیار متغیر تصادفی $$X$$ هستند.

تحقیق نامساوی چبیشف برای توزیع دو جمله‌ای و نرمال

در ادامه به بررسی نامساوی چبیشف برای توزیع گسسته دو جمله‌ای (Binomial Distribution) و پیوسته نرمال می‌پردازیم. همانطور که می‌دانید، باید برای هر دو حالت، ابتدا مقدار تابع بقا $$P(|X-\mu|>k\sigma)$$ را محاسبه کنیم. همچنین با توجه به مقدار $$k$$ طرف راست نامساوی یعنی $$\frac{1}{k^2}$$ را بدست آوریم. در انتها نیز این دو مقدار را بوسیله یک نمودار با یکدیگر مقایسه می‌کنیم. البته واضح است که نمودار ترسیم شده از منحنی تابع بقا همیشه در پایین نمودار حاصل از طرف راست نامساوی چبیشف قرار خواهد گرفت.

کد زیر که به زبان محاسباتی R نوشته شده است، به بررسی این نامساوی برای توزیع دو جمله‌ای با پارامترهای$$n=15$$ و $$p=0.5$$ پرداخته است. واضح است که مقدار $$k$$ از ۱ تا ۱۵ خواهد بود.

1n=15
2k =seq(1,n,1)
3p=0.5
4mu=n*p
5sigma=mu*(1-p)
6px=1-(pbinom(k*sigma+mu,n,p)-pbinom(mu-k*sigma,n,p))
7cb=1/(k^2)
8plot(k,px,xlab="k",ylab="P(|X-mu|>k*sigma)",ylim=c(0,6),col="red",lty=1,type="l")
9lines(k,cb,col="blue",lty=2)
10legend(10,6,legend=c("P(|X-mu|>k*sigma)","1/k^2"),col=c("red","blue"),lty=1:2,cex=1)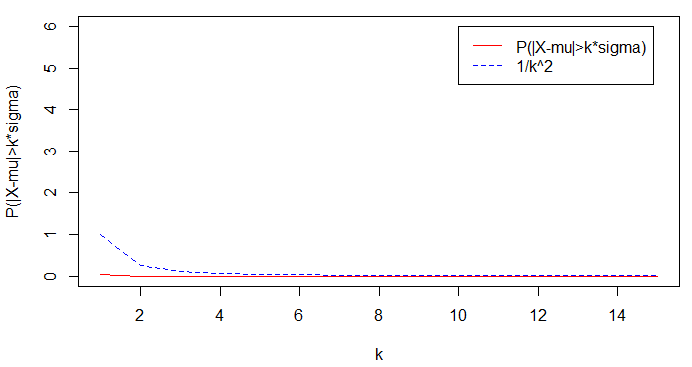

نکته: امید ریاضی و واریانس برای متغیر تصادفی دو جمله‌ای به ترتیب برابر با $$np$$ و $$np(1-p)$$‌ است.

این بار براساس توزیع نرمال این نمودار را ترسیم می‌کنیم. البته توجه داریم که میانگین توزیع از مقادیر $$X$$‌ کسر شده‌اند. کد زیر به این منظور نوشته شده است.

1mu=0
2sigma =1
3k=seq(0,5,0.01)
4px=1-pnorm(k*sigma+mu,mu,sigma)
5cb=1/(k^2)
6plot(k,px,xlab="k",ylab="P(|X-mu|>k*sigma)",ylim=c(0,10),col="red",lty=1,type="l")
7lines(k,cb,col="blue",lty=2)
8legend(3,10,legend=c("P(|X-mu|>k*sigma)","1/k^2"),col=c("red","blue"),lty=1:2,cex=1)

نتیجه اجرای این برنامه، به صورت نموداری مطابق تصویر زیر خواهد بود.

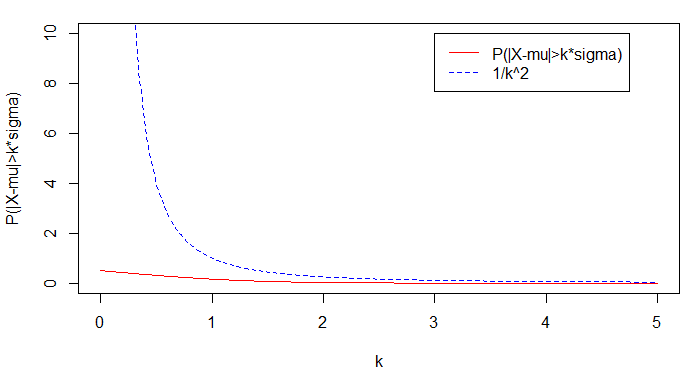
همانطور که گفتیم، نامساوی چبیشف برای مقادیر $$k>1$$ اهمیت پیدا می‌کند. در نمودارهای ترسیم شده نیز دیده می‌شود که برای مقادیر کوچکتر از ۱، نامساوی چبیشف منحنی مناسبی ارائه نمی‌کند زیرا مقداری بزرگتر از ۱ داشته و دارای فاصله بسیار زیادی از مقدار واقعی احتمال است. به همین دلیل اغلب مقادیر بزرگتر از ۱ را برای $$k$$ در نظر می‌گیرند.

کاربردهای نامساوی چبیشف

برای نشان دادن کاربرد نامساوی چبیشف به دو مثال می‌پردازیم تا قدرت آن را در زمانی که از توزیع احتمال مقادیر یا جامعه آماری اطلاع نداریم، نشان دهیم.

فیلم مجموعه آموزش آمار و احتمالات – از دروس دانشگاهی تا کاربردی در فرادرس

کلیک کنید

مثال ۱

در نظر بگیرید که در حوزه سرمایه‌گذاری در بازار بورس نزدک (NASDAQ) و داوجونز (Dow Jones)، شاخص بازگشت سرمایه (ROI) را اندازه‌گیری کرده‌ایم. اطلاعات مربوط به این دو شاخص به صورت زیر هستند.

$$Dow\; Jones\;:\;Average = 8.77\%, \;\;\;Standard\; Deviation= 14.43\%$$

$$NASDAQ\;:\;Average = 13.40\%, \;\;\;Standard\; Deviation= 24.80\%$$

با استفاده از نامساوی چبیشف با توجه به اینکه توزیع احتمالی این داده‌ها را نمی‌دانیم، می‌توانیم میزان شباهت نمونه (مقدار احتمال) با میانگین را برحسب ضرایب مختلف انحراف معیار (به عنوان فاصله با میانگین) بدست آوریم.

برای مثال، طبق نامساوی چبیشف متوجه می‌شویم که حداکثر ۷۵ درصد از مشاهدات بیشتر از ۲ انحراف معیار از میانگین فاصله دارند. به این ترتیب این ناحیه براساس هر دو شاخص به صورت زیر در خواهد آمد.

$$Dow\; Jones\;:\;-19.66\% --- 37.64\%$$

$$NASDAQ\;:\; = 35.42\% --- 62.85\%$$

با توجه به اینکه در بازار داو جونز این بازه کوچکتر است، در نتیجه شاخص بازگشت سرمایه در آن کم رونق‌تر است در عوض بازار نزدک از کارایی خوبی برخوردار است زیرا در اکثر مواقع نرخ بازگشت سرمایه مقدار بزرگتری از داو جونز دارد.

مثال ۲

همانطور که در توزیع نرمال می‌توان دید، روابط زیر برقرار است:

$$\large P(|X-\mu|<\sigma)=0.68$$

و

$$\large P(|X-\mu|<2\times \sigma)=0.95$$

همچنین

$$\large P(|X-\mu|<3\times \sigma)=0.99.7$$

ولی برطبق نامساوی چبیشف مقدار حداقل احتمال برحسب ضریب $$k$$ به شکل زیر خواهد بود.

$$\large \Pr(|X-\mu|<k \times \sigma)  >1-\dfrac{1}{k^2}$$

در نتیجه برای یک، دو و سه انحراف استاندارد فاصله از میانگین خواهیم داشت:

$$\large \Pr(|X-\mu|<\sigma)>1-1=0$$

که امری بدیهی است و در ادامه

$$\large \Pr(|X-\mu|<2\times \sigma)>1-\dfrac{1}{2^2}=1-\dfrac{1}{4}=0.75$$

$$\large \Pr(|X-\mu|<3\times \sigma)>1-\dfrac{1}{3^2}=1-\dfrac{1}{9}=0.1-0.11=0.89$$

همانطور که می‌بینید این مقادیر با نتایج حاصل از توزیع نرمال تفاوت زیادی دارند. این امر نشانگر آن است که کران‌های حاصل از نامساوی چبیشف تیز نبوده و با مقدار واقعی فاصله دارند.

خلاصه و جمع‌بندی

در این نوشتار به بررسی نامساوی چبیشف و اثبات آن پرداختیم. در این بین کاربردهایی نیز از این نامساوی معرفی کردیم. هر چند زمانی که توزیع احتمالی برای متغیر تصادفی مشخص باشد، استفاده از نامساوی چبیشف، کران تیزی ارائه نمی‌کند ولی به عنوان یک روش در استنباط ناپارامتری، معیار مناسبی خواهد بود. البته نامساویی‌هایی دیگری نیز وجود دارند که نسبت به نامساوی چبیشف کران‌های بهتر و تیزتری را ارائه می‌دهند که در مطالب دیگر مجله فرادرس به آن‌ها نیز خواهیم پرداخت.

در صورت علاقه‌مندی به مباحث مرتبط در زمینه ریاضی و آمار، آموزش‌های زیر نیز به شما پیشنهاد می‌شوند:

• مجموعه آموزش‌های آمار و احتمالات
• آموزش آمار و احتمال مهندسی
• مجموعه آموزش‌های ریاضی
• توزیع‌های آماری — مجموعه مقالات جامع وبلاگ فرادرس
• متغیر تصادفی و توزیع برنولی — به زبان ساده
• توزیع نرمال یک و چند متغیره — مفاهیم و کاربردها

^^