مول چیست؟ – به زبان ساده + تبدیلات، فرمول ها و مثال

مول یکی از واحدهای SI برای شمارش تعداد مشخصی از ذرات بسیار کوچک مانند اتم‌ها، مولکول‌ها، یون‌ها و الکترون‌ها است. واحد شمارش مول برابر با کمیت ثابت و مشخصی از یک ماده (معمولا گرم) است. یک مول برابر با تعداد عدد آووگادرو ذره است که مقداری برابر با $$6.02214076\times10^{23}$$ دارد. در این مطلب از مجله فرادرس می‌آموزیم مول چیست، چگونه به کار می‌رود و در چه محاسباتی استفاده می‌شود.

در ابتدای این مطلب می‌آموزیم مول چیست و چه ارتباطی با عدد آووگادرو دارد. سپس روش بیان واحد مول را آموخته و با مفاهیم و محاسبات مول آشنا می‌شویم. پس از آن با مول عناصر در ترکیبات و مفهوم جرم مولی آشنا می‌شویم. در ادامه، رابطه مول و جرم اتمی را درک کرده و روش‌های تبدیل مول به سایر واحدها را می‌آموزیم. در نهایت با کاربرد و تاریخچه مول آشنا می‌شویم. با مطالعه این مطلب تا انتها می‌توانید به شکلی کامل بیاموزید مول چیست.

مول چیست؟

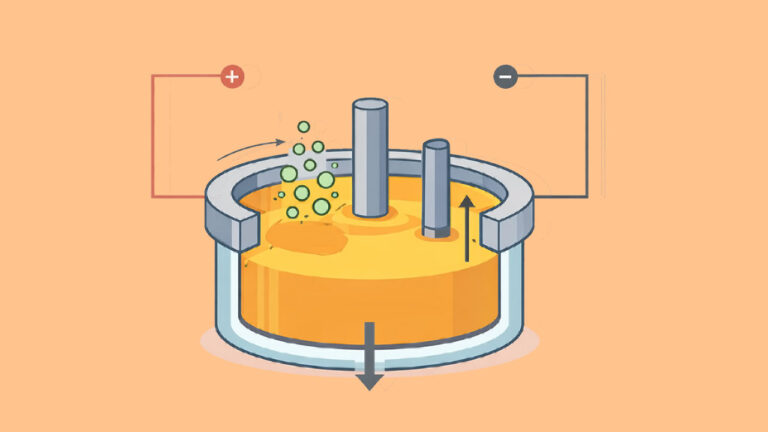
مول یکی از واحدهای اندازه‌گیری سیستم SI برای اندازه‌گیری تعداد ذرات بسیار ریز است. برای درک مفهوم مول باید در نظر بگیریم که یک مول از یک ذره برابر با تعداد عدد آووگادرو ($$6.022\times10^{23}$$) عدد از آن ذره است. ذرات سازنده مواد معمولا اتم، یون یا مولکول‌ها هستند. بنابر تعریف و شیوه اندازه‌گیری عدد آووگادرو، یک مول، مقدار مشخصی از یک ماده است که تعداد ذرات آن با تعداد ذرات ۱۲ گرم کربن خالص ۱۲ برابر است.

مفهوم مول با عبارت لاتین «Mole» شناخته می‌شود که یکی از معانی این کلمه، جرم زیاد یا توده است که با کاربرد این واژه به عنوان یکای اندازه‌گیری نیز همخوانی دارد. مفهوم مول مانند مفهوم جین که برابر با ۱۲ عدد است، یک واحد شمارش است و می‌تواند برای هر ذره ریزی به کار رود.

عدد آووگادرو چیست؟

مبدا مفهوم مول به شیمی - فیزیکدان ایتالیایی، «آمدئو آووگادرو» نسبت داده می‌شود. او در مقاله مهمی، در توضیح رفتار گازها پیشنهاد کرد که حجم‌های برابر از همه گازها در دمای یکسان و فشار برابر، تعداد یکسانی مولکول دارند. این فرضیه به نام فرضیه آووگادرو شناخته می‌شود و امروزه عدد ۶.۰۲۲۱۴۱۵ ضربدر ده به توان ۲۳ که نشان‌دهنده تعداد ذرات در یک مول است، به نام عدد آووگادرو شناخته می‌شود.

واحد مول چگونه بیان می شود؟

در قسمت قبل آموختیم مول چیست. واحد مول معمولا بر حسب واحد گرم بیان می‌شود. بنابر تعریف عبارت مول که تعداد عدد آووگادرو از ذرات ماده است، یک مول از یک ماده تعداد ذرات برابری با ۱ مول از ماده دیگر دارد. اما جرم یک مول از یک ماده با جرم ۱ مول از ماده دیگر متفاوت است زیرا جرم هر عنصر با عنصر دیگر متفاوت است.

برای مثال، یک مول از عنصر کربن خالص ۱۲ جرمی برابر با ۱۲ گرم دارد و یک مول از آب خالص، جرمی برابر با ۱۸ گرم دارد. اما تعداد ذراتی که در ۱۲ گرم کربن و ۱۸ گرم آب وجود دارد (۱ مول) با هم برابر است. برای درک بهتر این مفاهیم، به نکات زیر توجه کنید.

• ۱ مول از هر ماده ( الکترون، مولکول، عنصر، کاغذ، خودکار و ...) تعداد $$6.022\times10^{23}$$ از آن ماده است.
• برای ذرات ریز مانند عناصر، مقدار مول مواد بر حسب گرم آن‌ها سنجیده می‌شود.
• تعداد ذرات موجود در ۱ مول از یک ماده با تعداد ذرات موجود در ۱ مول از ماده دیگر برابر است.
• جرم ۱ مول از یک ماده با جرم ۱ مول از ماده دیگر متفاوت است.

برای درک بهتر این موضوع که یک مول ماده چیست، به مثال‌های زیر دقت کنید.

مثال ۱

چند عدد مولکول آسپرین با فرمول شیمیایی $$C_9H_8O_4$$ در ۰٫۰۱۳۹ مول آسپیرین وجود دارد؟

پاسخ

گفتیم که هر مول از ماده برابر با $$6.022\times10^{23}$$ ذره از ماده است. پس باید محاسبه کنیم ۰٫۰۱۳۹ مول از آسپرین چند مولکول آسپرین دارد. با ضرب این مقدار در عدد آووگادرو، تعداد مولکول‌های آسپرین به دست می‌آید.

$$0.0139{mol\ C_9H_8O_4} \times \frac{6.022 \times 10^{23}\ molecules\ C_9H_8O_4}{1 {mol\ C_9H_8O_4}} = 8.37 \times 10^{21}\ molecules\ C_9H_8O_4$$

مثال ۲

چند مول از مولکول آسپرین حاوی $$9.50 \times 10^{25}$$ مولکول آسپرین است؟

پاسخ

همانطور که آموختیم، هر مول حاوی تعداد $$6.022\times10^{23}$$ ذره (مولکول) از ماده است. پس برای یافتن تعداد مول ماده کافی است تعداد مولکول‌های داده شده را بر عدد آووگادرو تقسیم کنیم.

$$9.50 \times 10^{25} {molecules\ C_9H_8O_4} \times \frac{1\ mol\ C_9H_8O_4}{6.022 \times 10^{23} {molecules\ C_9H_8O_4}} = 158\ mol\ C_9H_8O_4$$

مثال ۳

اگر فرض کنیم تعداد ستاره‌ها در حهان برابر با $$7\times 10^{22}$$ ستاره است، چند مول ستاره داریم؟

پاسخ

برای پاسخ به این سوال کافی است تعداد ستاره‌ها را بر عدد آووگادرو تقسیم کنیم تا مول آن به دست آید.

$$\text{moles stars} = \frac{7 \times 10^{22}}{6.022 \times 10^{23}} = 0.116 \, \text{mol}$$

یادگیری شیمی‌دهم با فرادرس

در قسمت‌های قبل آموختیم مفهوم مول چیست. برای درک بهتر مول و محاسبات و مفاهیم مربوط به آن نیاز است ابتدا با مفاهیمی چون جرم اتمی میانگین، ساختار اتم، موازنه واکنش‌های شیمیایی و جرم مولی آشنا شویم. پیشنهاد می‌کنیم برای درک بهتر این مسائل و مفاهیم، به مجموعه فیلم آموزش دروس پایه دهم فرادرس، بخش شیمی مراجعه کنید که با زبانی ساده ولی کاربردی به توضیح این مفاهیم می‌پردازد.

همچنین، با مراجعه به فیلم‌های آموزش فرادرس که لینک آن‌ها در ادامه آورده شده است، می‌توانید به آموزش‌های بیشتری در زمینه مول دسترسی داشته باشید.

• فیلم آموزش علوم تجربی پایه نهم بخش شیمی فرادرس
• فیلم آموزش علوم تجربی پایه هشتم بخش شیمی فرادرس
• فیلم آموزش شیمی ۳ پایه دوازدهم فرادرس

مفاهیم و محاسبات مرتبط با مول

در قسمت‌های قبل آموختیم مول چیست. برای درک بهتر این مفهوم و مسائل و مفاهیم مرتبط با آن نیاز است با مفاهیمی مانند عدد آووگادرو، جرم مولی، درصد جرمی (ترکیب درصد) و ... آشنا باشیم. این مفاهیم در جدول زیر به اختصار توضیح داده شده است و در بخش‌های بعدی توضیح داده می‌شوند.

تعداد مول های عناصر در ترکیبات شیمیایی

تا اینجا آموختیم مول چیست. تعداد مول‌های یک عنصر در یک ترکیب شیمیایی برابر با اتم‌های آن عنصر در مولکول یا فرمول واحد از ترکیب شیمیایی است. برای مثال، ۱ مول گلوکز با فرمول شیمیایی $$C_6H_{12}O_6$$ شامل ۶ مول کربن، ۱۲ مول هیدروژن و ۶ مول اکسیژن است. هر یک از این نسبت‌ها بین ۱ مول از یک ماده و مول‌های عنصر، کسری را به ما می‌دهد که می‌توانیم از آن‌ها در محاسبات مختلف و درک واکنش‌های شیمیایی استفاده کنیم.

برای درک بهتر، به مثال‌های زیر دقت کنید.

مثال ۱

چند مول از عنصر هیدروژن در ۳ مول مولکول گلوکز وجود دارد؟

پاسخ

گفتیم که فرمول شیمیایی گلوکز، $$C_6H_{12}O_6$$ است. هر یک مول گلوکز با توجه به فرمول ترکیب شیمیایی آن، شامل ۱۲ مول عنصر هیدروژن است. پس ۳ مول گلوکز حاوی ۳۶ مول عنصر هیدروژن خواهد بود.

مثال ۲

تعداد مول های عنصر اکسیژن ر در ۰٫۵ مول از ماده‌ی $${Ca(NO_3)_2}$$ را حساب کنید.

پاسخ

با توجه به فرمول شیمیایی ماده کلسیم نیترات، در هر ۱ مول از این ترکیب شیمیایی، ۶ مول اکسیژن وجود دارد. در نتیجه در نیم مول از این ماده، ۳ مول عنصر اکسیژن وجود خواهد داشت.

جرم مولی چیست؟

در قسمت‌های قبل آموختیم مول چیست و چگونه شمارش می‌شود. گفتیم که مول را معمولا بر حسب گرم بیان می‌کنند. جرم مولی یکی از کمیت‌هایی است که برای بیان جرم ۱ مول از یک ماده بکار می‌رود و واحد اندازه‌گیری آن، گرم بر مول ($$\frac{gram}{mole}$$) است. شیمی‌دان‌ها به طور همزمان روی سطح اتم‌های فردی و نمونه‌هایی با اندازه‌ای که بتوان در آزمایشگاه با آن کار کرد، فعالیت می‌کنند.

برای انتقال بین این دو مقیاس، آن‌ها باید بدانند چند اتم یا مولکول در نمونه‌ای که با آن کار می‌کنند وجود دارد. مفهومی که این دو مقیاس را به هم وصل می‌کند، جرم مولی است. جرم مولی یک عنصر یا ترکیب، مقداری است که می‌توان آن را به‌راحتی با ترازوی آزمایشگاهی اندازه‌گیری کرد، اما جرم یک اتم یا مولکول آن‌قدر کوچک است که اندازه‌گیری‌ آن دشوار است. به همین دلیل، در محاسبات استوکیومتری معمولا از مول استفاده می‌شود.

جرم مولی اتم‌ها

جرم اتمی ارائه شده در جدول تناوبی برای اتم‌های مختلف، همان جرم مولی عناصر بر حسب گرم بر مول در نظر گرفته می‌شود. برای مثال، جرم اتمی هیدروژن در جدول تناوبی ۱٫۰۰۸ گزارش شده است پس جرم مولی آن برابر با ۱٫۰۰۸ است.

جرم مولی مولکول ها

جرم مولی یک مولکول برابر با مجموع جرم اتمی (جرم مولی) اتم‌های تشکیل دهنده آن است. در محاسبه این جرم مولی، فرمول شیمیایی واحد مولکول در نظر گرفته می‌شود. برای مثال، جرم مولی آب برابر با جمع جرم مولی دو اتم هیدروژن و جرم مولی یک اتم اکسیژن است.

$$M_{H_2O}=M_{H_2} + M_O=2+16=18 \frac{g}{mol}$$

به عبارت دیگر، برای محاسبه جرم مولی یک ترکیب، باید ابتدا جرم اتمی عناصر سازنده را از جدول تناوبی پیدا کرده، سپس هر کدام را در تعداد اتم‌های آن عنصر در فرمول ترکیب ضرب کرده و در نهایت همه این مقادیر را با هم جمع کرد. این فرآیند در مثال‌های بعدی توضیح داده شده است.

مثال ۱

جرم مولی سدیم هیدروکسید با فرمول شیمیایی $$NaOH$$ چیست؟

پاسخ

ابتدا جرم اتمی اتم‌های سازنده این مولکول را با استفاده از جدول تناوبی به دست می‌آوریم. جرم مولی سدیم برابر با ۲۲٫۹۹۰ گرم بر مول، جرم مولی اکسیژن برابر با ۱۵٫۹۹۹ گرم بر مول و جرم مولی هیدروژن برابر با ۱٫۰۰۸ گرم بر مول است. سپس این مقادیر را در تعداد اتم‌ها ضرب کرده و با هم جمع می‌کنیم. در این ترکیب شیمیایی، از هر عنصر ۱ عدد وجود دارد پس جرم مولی آن به شکل زیر به دست می‌آید.

$$1 \times 22.990\ g.mol^{-1}\ Na + 1 \times 15.999\ g.mol^{-1}\ O + 1 \times 1.008\ g.mol^{-1}\ H = 39.997\ g.mol^{-1}\ NaOH$$

مثال ۲

جرم مولی مولکول نیترات کلسیم با فرمول شیمیایی $$Ca(NO_3)_2$$ چیست؟

پاسخ

ابتدا جرم اتمی عناصر سازنده این ماده را با استفاده از جدول تناوبی به دست می‌آوریم. جرم اتمی کلسیم برابر با ۴۰٫۰۷۸ گرم بر مول، نیتروژن ۱۴٫۰۰۷ گرم بر مول و اکسیژن ۱۵٫۹۹۹ گرم بر مول است. سپس این مقادیر را در تعداد عناصر ضرب می‌کنیم. دقت داشته باشید دو واحد $$NO_2$$ در ساختار این مولکول وجود دارد. این بدین معنی است که دو اتم نیتروژن و ۴ اتم اکسیژن در این مولکول وجود دارد. پس برای محاسبه جرم اتمی این مولکول به شکل زیر عمل می‌کنیم.

$$1 \times 40.078\ Ca + 2 \times 14.007\ N + 6 \times 15.999\ O = 164.008\ g.mol^{-1}\ Ca(NO_3)_2$$

پیشنهاد می‌کنیم برای درک بهتر مفهوم جرم مولی، فیلم آموزش جرم مولی شیمی‌دهم فرادرس که لینک آن در ادامه آورده شده است را مشاهده کنید.

رابطه مول و جرم اتمی

از آنجا که تعریف هر دو واحد مول و یکای جرم اتمی بر پایه ماده مرجع مشترک ایزوتوپ پایدار کربن -۱۲ انجام شده است، جرم مولی هر ماده «از نظر عددی» برابر با جرم اتمی یا جرم فرمولی آن ماده بر حسب واحد جرم اتمی است.

در قسمت قبل آموختیم مول چیست و چگونه بیان می‌شود. طبق تعریف مول، ۱۲ گرم کربن -۱۲ شامل یک مول از اتم‌های کربن -۱۲ است. یعنی جرم مولی آن ۱۲ گرم بر مول در نظر گرفته می‌شود. همچنین، بر اساس تعریف واحد جرم اتمی، جرم یک اتم کربن -۱۲ برابر با ۱۲ واحد جرم اتمی است.

به همین ترتیب می‌توان گفت که جرم مولکولی یک ترکیب شیمیایی بر حسب گرم با جرم فرمولی آن ترکیب بر حسب واحد جرم اتمی amu از نظر عددی برابر است. برای درک بهتر این مفهوم به جدول زیر دقت کنید.

تبدیل گرم به مول و بالعکس

یکی از کاربردهای مفهوم مول و محاسبه آن در مسائل استوکیومتری، تبدیل گرم به مول و تبدیل مول به گرم است. جرم مولی بر حسب گرم بر مول ($$\frac{g}{mol}$$) یک ضریب تبدیل برای تبدیل تعداد مول یک ماده به جرم آن بر حسب گرم است.

همچنین، عکس جرم مولی بر حسب مول بر گرم ($$\frac{mol}{g}$$) یک ضریب تبدیل برای تبدیل جرم ماده بر حسب گرم به تعداد مول آن است.

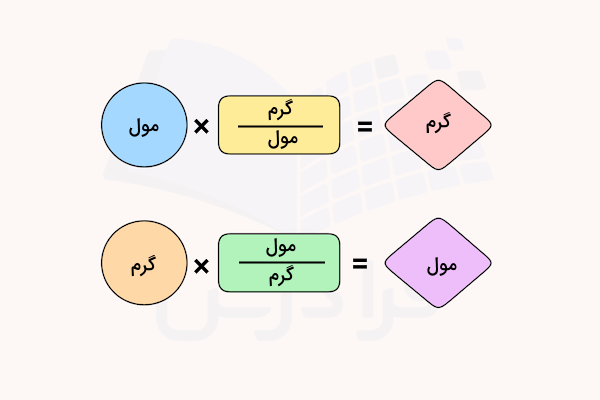
این تبدیل‌ها را در مثال‌های زیر بررسی می‌کنیم.

مثال ۱

چند گرم آب در ۲٫۵ مول آب وجود دارد؟

پاسخ

برای پاسخ به اینگونه سوالات، ابتدا جرم مولی ماده را محاسبه می‌کنیم. جرم مولی آب به شکل زیر به دست می‌آید.

$$2 \times 1.008\ g \cdot mol^{-1}\ H + 15.999\ g \cdot mol^{-1}\ O = 18.02\ g \cdot mol^{-1}\ H_2O$$

سپس برای تبدیل مول به گرم، از ضریب تبدیل جرم مولی آب استفاده می‌کنیم و آن را در تعداد مول داده شده در صورت سوال ضرب می‌کنیم. بدین ترتیب، گرم آن به دست می‌آید.

$$2.50 \cancel{mol\ H_2O} \times \frac{18.02\ g\ H_2O}{1 \cancel{mol\ H_2O}} = 45.1\ g\ H_2O$$

مثال ۲

چند مول آسپرین در ۲٫۵ گرم از این ماده وجود دارد؟ فرمول شیمیایی آسپرین $$C_9H_8O_4$$ است.

پاسخ

برای محاسبه تعداد مول آسپرین در ۲٫۵ گرم از آن، ابتدا باید جرم مولی آن را محاسبه کنیم. این محاسبات به شکل زیر انجام می‌شود.

$$9 \times 12.01\, C + 8 \times 1.008\, H + 4 \times 16.00\, O = 180.16\, g/mol$$

سپس با استفاده از ضریب تبدیل عکس جرم مولی، تعداد مول موجود در جرم داده شده از ماده را به دست می‌آوریم.

$$2.5 \cancel{~g~C_9H_8O_4} \times \frac{1~mol~C_9H_8O_4}{180 \cancel{~g~C_9H_8O_4}} = 0.0193~mol~C_9H_8O_4 \nonumber$$

مثال ۳

چند مول سدیم هیدروکسید در ۱۰ گرم از این ماده وجود دارد؟

پاسخ

مانند مثال‌های قبل، ابتدا جرم مولی سدیم هیدروکسید را محاسبه می‌کنیم.

$$22.99~g \cdot mol^{-1}~Na + 16.00~g \cdot mol^{-1}~O + 1.01~g \cdot mol^{-1}~H = 40.00~g \cdot mol^{-1}~NaOH$$

سپس با استفاده از ضریب تبدیل عکس جرم مولی، تعداد مول ماده را به دست می‌آوریم.

$$10.0 \cancel{~g~NaOH} \times \frac{1~mol~NaOH}{40.00 \cancel{~g~NaOH}} = 0.250~mol~NaOH$$

تبدیل تعداد اتم به جرم

در برخی از مسائل استوکیومتری مربوط به مول، نیاز است تا تعداد اتم داده شده را به جرم ماده تبدیل کنیم. تا اینجا آموختیم مول چیست و چگونه می‌توان واحد مول را با استفاده از عدد آووگادرو بیان کرد و تعداد اتم‌ها را به مول و بالعکس تبدیل کرد. در حل مسائلی که در آن‌ها نیاز است تعداد اتم‌ها به جرم ماده تبدیل شود، از عدد آووگادرو و جرم مولی ماده استفاده می‌کنیم.

برای درک بهتر این محاسبات، به مثال‌های زیر دقت کنید.

مثال ۱

تعداد اتم‌های مس را در یک نمونه ۴۴٫۵۲ گرمی مس محاسبه کنید.

پاسخ

با توجه به توضیحات قسمت قبل، برای تبدیل جرم به تعداد اتم باید جرم را بر جرم مولی تقسیم کرده سپس در عدد آووگادرو ضرب کنیم.

$$\frac{44.52~g~Cu}{63.55~g/mol} \times 6.022 \times 10^{23}~\text{atoms/mol} = 4.22 \times 10^{23}~\text{atoms}$$

مثال ۲

اگر تعداد $$7.47\times10^{24}$$ اتم در نمونه $$Na_2CO_3$$ وجود داشته باشد، جرم نمونه را محاسبه کنید.

پاسخ

همانطور که در قسمت قبل مشاهده کردیم، برای تبدیل تعداد اتم به جرم کافی است تعداد اتم را بر عدد آووگادرو تقسیم کرده سپس در جرم مولی ضرب کنیم. اما باید توجه داشته باشیم در این سوال، تعداد یک عنصر در یک ترکیب شیمیایی مشخص شده است پس باید نسبت مولی عنصر به ترکیب شیمیایی را نیز در نظر بگیریم. در هر مولکول سدیم کربنات، ۲ اتم سدیم وجود دارد. محاسبات این سوال به شکل زیر است.

$$\frac{7.47 \times 10^{24}Na }{2} = 3.735 \times 10^{24}{Na_2CO_3}$$

$$\frac{3.735 \times 10^{24}}{6.022 \times 10^{23}} = 6.20~\text{mol}_ \ce{Na2CO3}\times 105.99~\frac{g}{mol} = 657.14~g$$

تبدیل مول به حجم گاز و بالعکس

بر اساس قانون گاز ایده‌آل، یک مول از هر گاز ایده‌آلی در شرایط استاندارد، حجمی برابر با ۲۲٫۴ لیتر دارد. با استفاده از این رابطه، می‌توان مول و حجم بسیاری از مواد را در واکنش‌های شیمیایی مختلفی که حاوی فرآورده گازی هستند، محاسبه کرد.

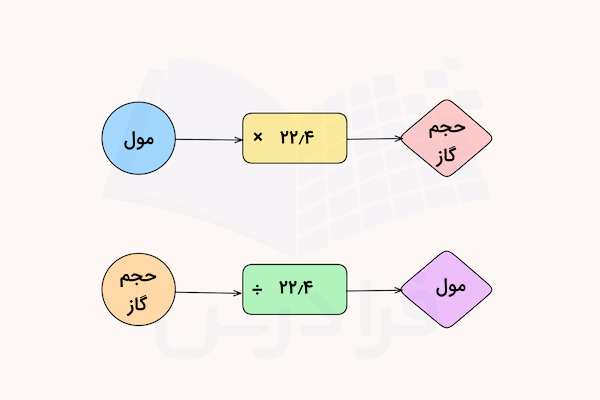
برای درک بهتر این محاسبات با استفاده از مفهوم مول، به مثال‌های زیر دقت کنید.

مثال ۱

بسیاری از فلزات با اسیدها واکنش می‌دهند و گاز هیدروژن آزاد می‌کنند. یک واکنش مشخص، حدود ۸۶٫۵ لیتر گاز هیدروژن را در شرایط استاندارد آزاد می‌کند. چند مول گاز هیدروژن طی این واکنش آزاد شده است؟

پاسخ

برای پاسخ به این سوال، به سادگی با تقسیم حجم گاز بر عدد ۲۲٫۴ تعداد مول آن به دست می‌آید.

$$86.5\ L\ H_2 \times \frac{1\ mol\ H_2}{22.4\ L\ H_2} = 3.86\ mol\ H_2$$

مثال ۲

اگر در شرایط استاندارد، مقدار ۸۶۷ لیتر گاز نیتروژن از واکنش آزاد شود، جرم آن چقدر است؟

پاسخ

برای پاسخ به این سوال، ابتدا مول گاز را با تقسیم حجم آن بر ۲۲٫۴ به دست آورده و سپس با استفاده از جرم مولی آن، جرم نیتروژن را به دست می‌آوریم.

$$867 \: \text{L} \times \frac{1 \: \text{mol}}{22.4 \: \text{L}} = 38.7 \: \text{mol}\nonumber$$

$$38.7\ mol \times \frac{28\ g}{1\ mol} = 1083.6\ g\ N_2$$

ترکیب درصد چیست؟

ترکیب درصد یک مولکول تعیین می‌کند که هر عنصر چه درصدی از جرم کلی یک ترکیب شیمیایی را تشکیل می‌دهد. برای محاسبه ترکیب درصد یک عنصر در یک ترکیب شیمیایی، کافی است جرم مولی آن عنصر را به جرم مولی کل ترکیب شیمیایی تقسیم کنیم.

برای مثال، مولکول هیدروژن کلرید (اسید کلریدریک) را در نظر بگیرید. نسبت هیدروژن در این ترکیب بر حسب جرم مولی به شکل زیر نوشته می‌شود.

$$\frac{1.008\frac{g}{mol}}{36.46\frac{g}{mol}} \nonumber$$

حال با ضرب این نسبت در عدد ۱۰۰، مقدار ترکیب درصد هیدروژن در اسید کلریدریک به دست می‌آید.

$$0.02765\times 100=2.765\% \nonumber$$

برای درک بهتر این مفهوم، به مثال‌های زیر دقت کنید.

مثال ‍۱

مقدار درصد کلسیم در ترکیب $$CaF_2$$ و جرم آن را در ۴۲۳٫۶ گرم از این ماده محاسبه کنید.

پاسخ

ترکیب درصد کلسیم در کلسیم فلوئورید با تقسیم جرم مولی کلسیم بر جرم مولی کلسیم فلوئورید ضرب در عدد ۱۰۰ به دست می‌آید.

$$\frac{40.08g\; Ca}{{78.08g\; CaF_{2}}} \times 100=51 \%$$

برای به دست آوردن مقدار گرم کلسیم در جرم داده شده از کلسیم فلوئورید، باید جرم داده شده را بر جرم کلسیم فلوئورید تقسیم کنیم تا مول کلسیم فلوئورید به دست آید. از آنجا که در هر مول کلسیم فلوئورید، ۱ مول کلسیم وجود دارد، می‌توانیم با ضرب تعداد مول کلسیم فلوئورید در جرم مولی کلسیم، تعداد مول کلسیم را به دست آوریم.

$$(423.6g\; CaF_{2})\times \left ( \frac{1mol}{78.08g\; CaF_{2}} \right )\times \left ( \frac{40.08g\; Ca}{1mol\; Ca}\right )=x\: g\; Ca=217.4\: g\; Ca \nonumber$$

مثال ۲

اسید سولفوریک با فرمول شیمیایی $$H_2SO_4$$ پرکاربردترین ماده شیمیایی در صنایع مختلف است. اگر یک نمونه از اسید سولفوریک شامل ۳٫۶۷ گرم هیدروژن باشد، چند گرم گوگرد در آن وجود خواهد داشت؟

پاسخ

برای پاسخ به این سوال، ابتدا جرم مولی اسید سولفوریک را با استفاده از جدول تناوبی عناصر به دست می‌آوریم.

$$\text{M}_{ \text{H}_2\text{SO}_4} = (2 \times 1.008) + 32.06 + (4 \times 16.00) = 98.076\ \text{g/mol}$$

سپس ترکیب درصد گوگرد و هیدروژن را در نمونه به دست می‌آوریم.

$$\%\ \text{H} = \frac{2.016}{98.076} \times 100 \approx 2.055\%$$

$$\%\ \text{S} = \frac{32.06}{98.076} \times 100 \approx 32.69\%$$

فرض می‌کنیم در نمونه داده‌شده، ۳٫۶۷ گرم هیدروژن وجود دارد. حالا می‌خواهیم بدانیم چند گرم گوگرد دارد. از نسبت درصدها در فرمول ترکیب درصد استفاده می‌کنیم:

$$\frac{3.67}{2.055} = \frac{x}{32.69}$$

$$x = \frac{3.67 \times 32.69}{2.055} \approx \boxed{58.36\ \text{g S}}$$

استفاده از مول در محلول ها

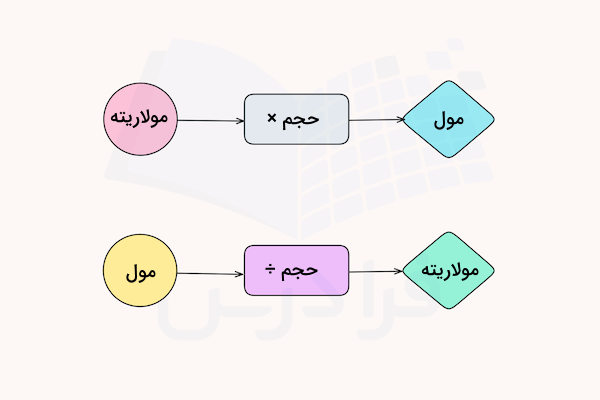
یکی از رایج ترین روش‌های بیان غلظت محلول‌های مختلف، استفاده از مفهوم مولاریته است. مولاریته یک محلول، تعداد مول های ماده حل شونده را در لیتر محلول مشخص می‌کند، با فرمول زیر محاسبه می‌شود و واحد اندازه‌گیری آن، مول بر لیتر است.

$$M=\frac{n}{V}$$

در فرمول بالا M نماد مولاریته، n تعداد مول ماده حل‌شونده و V حجم محلول است. می‌توان از تبدیل گرم به مول که در قسمت‌های قبل آموختیم استفاده کرد و مقدار مولاریته محلول‌ها را به دست آورد. برای درک بهتر این محاسبات، به مثال‌های زیر دقت کنید.

مثال ۱

چه جرمی از سدیم کلرید باید در ۲۵۰ میلی لیتر از این محلول حل شود تا محلول ۰٫۵ مولار سدیم کلرید به دست آید؟

پاسخ

برای محاسبه جرم سدیم کلرید، ابتدا از مفهوم مولاریته و حجم استفاده می‌کنیم تا تعداد مول مورد نیاز سدیم کلرید را پیدا کنیم.

$$M = 0.500~mol/L\, \quad V = 250~mL = 0.250~L$$

$$n = M \times V = 0.500 \times 0.250 = 0.125~mol$$

سپس با استفاده از جرم مولی سدیم کلرید می‌توانیم جرم آن را به دست اوریم.

$$m = n \times M_{NaCl} = 0.125 \times 58.44 = 7.305~g$$

مثال ۲

مقدار مولاریته محلولی که با استفاده از حل کردن ۱۰ گرم پتاسیم برمید در آب برای ۵۰۰ میلی‌لیتر محلول تهیه شده است را محاسبه کنید.

پاسخ

برای محاسبه مولاریته محلول ابتدا جرم مولی پتاسیم برمید را محاسبه کرده و سپس تعداد مول آن را با استفاده از تقسیم جرم بر جرم مولی به دست می‌آوریم.

$$M_{KBr} = 39.10 + 79.90 = 119.00~g/mol$$

$$n = \frac{m}{M_{KBr}} = \frac{10.0}{119.00} = 0.08403~mol$$

با تقسیم تعداد مول بر حجم محلول بر حسب لیتر، مولاریته به دست می‌آید.

$$M = \frac{n}{V} = \frac{0.08403}{0.500} = 0.1681~mol/L$$

فرمول مولکولی و فرمول تجربی

فرمول مولکولی مواد مختلف، نسبت واقعی ترکیب عناصر تشکیل دهنده آن‌ها را مشخص می‌کند. در مطالعه مواد شیمیایی می‌آموزیم فرمول شیمیایی مواد و ترکیبات شیمیایی مختلف، شکل ثابتی دارد که نسبت مولی عناصر در آن‌ها همواره ثابت است.

روش‌هایی که شیمیدان‌ها در آزمایشگاه برای تعیین ترکیب مواد شیمییایی استفاده می‌کنند، فرمول مولکولی یک ترکیب را به شکل مستقیم به دست نمی‌آورد. بلکه فقط نسبت ساده‌ی صحیح عناصر موجود در ترکیب را مشخص می‌کند. به چنین فرمولی، فرمول تجربی گفته می‌شود. پیشنهاد می‌کنیم برای درک بهتر این فرمول‌های شیمیایی، مطلب روش تعیین فرمول مولکولی و فرمول تجربی مجله فرادرس را مطالعه کنید.

رابطه فرمول مولکولی و تجربی

برای مثال، فرمول مولکولی ماده گلوکز $$C_6H_{12}O_6$$ است اما ساده‌ترین نسبت صحیح عناصر در گلوکز $$CH_{2}O$$ است. اگر تمامی زیروندهای این فرمول تجربی در عدد ۶ ضرب شوند، فرمول مولکولی گلوکز به دست می‌آید. نکته مهم این است که فرمول تجربی را تنها می‌توان با دانستن جرم مولی به فرمول مولکولی تبدیل کرد. برای این کار با تقسیم جرم مولی ترکیب شیمیایی به جرم مولی فرمول تجربی می‌توان ضریب مورد نیاز برای تبدیل فرمول تجربی به فرمول مولکولی را به دست آورد.

برای مثال، با تقسیم جرم مولی استیک اسید بر جرم مولی فرمول تجربی آن ( $$CH_{2}O$$ ) به عدد ۲ می‌رسیم. با ضرب ضریب ۲ در تعداد عناصر فرمول تجربی این ماده می‌توانیم به فرمول مولکولی آن دست یابیم.

$$n=\frac{60.05\; g/mol}{30.02\; g/mol}=2 \nonumber$$

در نتیجه، فرمول مولکولی استیک اسید، $$C_2H_4O_2$$ خواهد بود. برای درک بهتر این محاسبات، به مثال‌های زیر دقت کنید.

مثال ۱

یک ترکیب دارای جرم مولی ۵۸٫۱۲ گرم بر مول و فرمول تجربی $$C_2H_5$$ است. فرمول مولکولی این ترکیب را تعیین کنید.

پاسخ

برای پیدا کردن فرمول مولکولی کافی است تا جرم مولی را بر جرم مولی فرمول تجربی تقسیم کنیم. جرم مولی فرمول تجربی $$C_2H_5$$ با توجه به جرم اتمی عناصر برابر با ۲۹٫۰۶ گرم بر مول است.

$$n = \frac{58.12}{29.06} = 2$$

پس جرم مولکولی این ماده $$C_4H_{10}$$ است.

مثال ۲

بنزن یک ترکیب مهم است که در ساخت پلاستیک‌ها، داروها، رنگ‌ها، مواد شوینده و آفت‌کش‌ها استفاده می‌شود. فرمول تجربی بنزن CH و جرم مولی آن ۷۸٫۱۱ گرم بر مول است. فرمول مولکولی آن را مشخص کنید.

پاسخ

مانند مثال قبل عمل کرده و جرم مولی فرمول تجربی را به دست می‌آوریم و جرم مولی ماده را بر آن تقسیم می‌کنیم.

$$n = \frac{78.11}{13.018} = 6$$

پس فرمول مولکولی بنزن $$C_6H_{6}$$ است.

کاربرد مول در شیمی و زندگی

مفهوم مول و محاسبات مربوط به آن به ما این امکان را می‌دهد تا واکنش‌های شیمیایی پیچیده را به داده‌هایی ساده و کاربردی تبدیل کنیم. تبدیل‌هایی مانند تبدیل جرم مولی به جرم ماده و ... محاسبات استوکیومتری و ترمودینامیک را آسان کرده و به ما این امکان را می‌دهند تا به درک بیشتری از واکنش‌های شیمیایی برسیم.

مزیت استفاده از جرم مولی به جای وزن مولکولی در کاربرد عملی آن در محاسبات شیمیایی نهفته است. جرم مولی که بر حسب گرم بر مول (g/mol) بیان می‌شود، به شیمی‌دان‌ها این امکان را می‌دهد تا مستقیما جرم ماده‌ای که روی ترازو در آزمایشگاه اندازه‌گیری می‌شود را به تعداد مول‌ها ربط دهند که در نهایت به تعداد ذرات یا اتم‌ها، مولکول‌ها و ... مربوط می‌شود.

مفهوم مول کاربردهای عملی فراوانی در زندگی روزمره ما دارد. شرکت‌های داروسازی برای اندازه‌گیری دقیق مواد فعال در داروها از مول استفاده می‌کنند، دانشمندان محیط زیست برای اندازه‌گیری غلظت آلاینده‌ها، و مهندسان شیمی برای طراحی و بهینه‌سازی فرآیندهای صنعتی از مول بهره می‌برند.

یادگیری شیمی عمومی با فرادرس

در این مطلب آموختیم مفهوم مول چیست و چگونه محاسبه می‌شود. یادگیری مفهوم مول نیازمند آشنایی با مفاهیمی چون ایزوتوپ‌ها، رفتار گاز‌ها، گاز ایده‌آل، انواع محلول و ... است. با شناخت این مفاهیم و به کمک مفهوم مول می‌توان بسیاری از مسائل استوکیومتری در محلول‌ها و در سایر فازها را حل کرد. پیشنهاد می‌کنیم برای یادگیری بهتر این مفاهیم، به مجموعه فیلم آموزش شیمی عمومی دانشگاه مراجعه کنید که این مفاهیم را با زبانی ساده ولی کاربردی توضیح می‌دهد.

همچنین با مراجعه به فیلم‌های آموزش فرادرس که در ادامه آورده شده است می‌توانید به آموزش‌های بیشتری در زمینه مول دسترسی داشته باشید.

• فیلم آموزش شیمی عمومی ۱ و ۲ با مرور و حل مساله
• فیلم آموزش آزمایشگاه شیمی عمومی 
• فیلم آموزش شیمی عمومی ۲ 

تاریخچه مول

مفهوم مول برای بیان تعداد ذرات موجود در یک مقدار مشخص از ماده طراحی شده و ریشه در نظریه اتمی دارد. این واژه اولین بار در سال ۱۸۹۶ توسط «ویلهلم اوستوالد» (Wilhelm Ostwald) معرفی شد، اما ایده اصلی آن به کارهای دانشمندانی چون «جان دالتون» (John Dalton) و «آمدئو آووگادرو» (Amedeo Avogadro) در قرن نوزدهم برمی‌گردد. آووگادرو با قانون خود بیان کرد که حجم‌های مساوی از گازها در شرایط یکسان، تعداد برابری مولکول دارند، که این پایه‌گذار مفهوم عدد آووگادرو شد.

در سال ۱۹۷۱، مول به‌عنوان یکی از هفت واحد پایه در سیستم بین‌المللی (SI) به رسمیت شناخته شد. این واحد نقش مهمی در شیمی و علوم کاربردی ایفا می‌کند، چرا که با استفاده از آن می‌توان مقدار مواد را به صورت دقیق محاسبه و در واکنش‌های شیمیایی به کار برد. مول ارتباط بین جرم ماکروسکوپی و تعداد ذرات میکروسکوپی را فراهم می‌کند.

آزمون محاسبات مول

در این مطلب آموختیم مول چیست و چگونه محاسبه می‌شود. برای درک بهتر آنچه در این مطلب از مجله فرادرس آموختید، به سوالات زیر پاسخ دهید. پس از پاسخ به تمرین‌ها می‌توانید با کلیک بر گزینه «مشاهده نتیجه آزمون»، نمره خود را مشاهده کنید.