محلول بافر — از صفر تا صد

مخلوطی از اسید ضعیف و باز مزدوج آن را محلول بافر یا به شکل سادهتر، بافر میگویند. زمانی که مقدار کمی اسید یا باز قوی به محلولهای بافر اضافه شود، این محلولها در مقابل pH از خود مقاومت نشان میدهند. محلولی از استیک اسید با فرمول $$CH_3COOH$$ و سدیم استات با فرمول $$CH_3COONa$$، مثالی از یک محلول بافر شامل یک اسید ضعیف و نمک آن است. در مثالی دیگر نیز میتوان به محلول آمونیاک و آمونیوم کلرید اشاره کرد.
بافرها
همانطور که اشاره شد، به هنگام اضافه کردن یک اسید یا باز قوی به محلول بافر، این محلول در مقابل تغییرات pH مقاوم خواهد بود. در نتیجه، از محلولهای بافر برای جلوگیری از تغییرات در pH یک محلول، فارغ از نوع حلشونده آن میتوان استفاده کرد. از محلولهای بافر به عنوان ابزاری برای ثابت نگهداشتن مقدار pH در بسیاری از فرآیندهای شیمیایی بهره میگیرند.
لازم به ذکر است که خون، یک محلول بافر به شمار میآید. دلیل مقاوم بودن محلولهای بافر به تغییرات pH، وجود تعادل بین اسید $$HA$$ و باز مردوج آن $$A ^ -$$ است. واکنش تعادلی در محلول بافر را میتوانید در پایین ملاحظه کنید:
$$\mathrm { HA } \rightleftharpoons \mathrm { H } ^ { + } + \mathrm { A } ^ { - }$$
زمانی که مقداری اسید قوی $$H ^ + $$ به محلول تعادلی اسید ضعیف و باز مزدوج آن اضافه شود، بر اساس اصل لوشاتلیه، تعادل به طرف چپ پیشروی خواهد کرد. این مورد سبب میشود تا غلظت یون هیدروژن $$H ^ +$$ به اندازهای که انتظار میرود، افزایش پیدا نکند. به طور مشابه، اگر یک باز قوی به محلول اضافه شود، کاهش یون هیدروژن، از مقدار مورد انتظار کمتر خواهد بود. دلیل این امر، پیشروی واکنش به طرف راست، برای جبران کمبود یون هیدروژن است.
سیستم بافری چیست؟
همانطور که در ابتدای متن نیز به آن اشاره شد، سیستم بافری به سیستمی میگویند که در یک محلول، مقادیر قابل توجهی اسید ضعیف و باز مزدوج آن یا باز ضعیف و اسید مزدوج آن وجود داشته باشد.
بافر بودن خون
محلولهای بافر کاربردهای گستردهای دارند. به طور مثال، در بیولوژی، محلولهای بافر برای حفظ مقدار صحیح pH و تنظیم عملکرد پروتئینها بکار میروند. اگر میزان pH، خارج از دامنه مورد نظر در پروتئین باشد، پروتئین شکسته و عملکرد آن متوقف میشود. محلول بافر شامل کربنیک اسید و بیکربنات در پلاسمای خون، pH را بین 7/35 تا 7/45 نگه میدارد. در صنعت، از محلولهای بافر در فرآیندهای تخمیری و رنگرزی استفاده میشود.

آمادهسازی یک محلول بافر
از سه روش کلی میتوان محلولهای بافر را تولید کرد. در روش اول، ابتدا اسیدِ بافر را در آب حل کنید. مقدار آب باید ۶۰ درصد حجم نهایی بافر باشد. سپس pH را اندازهگیری کنید. برای افزایش pH به مقدار مورد نظر، از یک باز قوی همچون $$NaOH$$ استفاده کنید. اگر بافر را به کمک یک باز تهیه کردهاید، در این مرحله میتوانید از یک اسید قوی همچون $$HCl$$ استفاده کنید.
در روش دوم، میتوانید محلول را در شکلهای اسیدی و بازی خود تولید کنید. به همین منظور، هر دو محلول باید غلظت بافر یکسان و برابر با بافر نهایی داشته باشند. برای بدست آوردن محلول بافر نهایی، همزمان با کنترل کردن میزان pH، یکی از محلولها را به دیگری اضافه میکنیم.
در روش سوم، به طور دقیق میتوانید میزان اسید و باز مزدوج مورد نیاز برای تولید یک محلول بافر با میزان مشخصی از pH را تعیین کنید. برای این کار باید از «معادله هندرسون–هاسلبالخ» $$(Henderson-Hasselbalch)$$ استفاده کنید که در زیر آمده است:
$$\mathrm { pH } = \mathrm { p } \mathrm { K } _ { \mathrm { a } } + \log \left( \frac { \left[ \mathrm { A } ^ { - } \right] } { [ \mathrm { HA } ] } \right)$$
در رابطه بالا:
- $$pH$$: میزان pH محلول بافر یا به عبارت دیگر، غلظت یون هیدروژن $$[ H ^ +]$$
- $$p K _ a $$: ثابت تفکیک اسید
- $$[\text{A}-] $$ و $$[\text{HA}]$$، غلظتهای باز مزدوج و اسید
تهیه بافر آمونیاکی
برای تهیه بافر آمونیاکی میتوانید از روشهای زیر استفاده کنید:
- تهیه بافر آمونیاکی با $$pH = 10$$: مقدار ۵/4 گرم آمونیوم کلرید را در 20 میلیلیتر آب حل کنید. مقدار 35 میلیلیتر از یک محلول 10 مولار آمونیاک را به آن اضافه و با آب رقیق کنید تا به حجم 100 میلیلیتر برسید.
- تهیه بافر آمونیاکی با $$pH = 10.9$$: l مقدار 67/5 گرم آمونیوم کلرید را در مقدار کافی محلول 10 مولار آمونیاک حل کنید تا به حجم 1000 میلیلیتر برسید.

معنای pH در یک بافر
در شیمی، pH معیاری برای سنجش غلظت یون هیدروژن در محلول است. pH یک بافر را میتوان از غلظتهای اجزای مختلف واکنش محاسبه کرد. واکنش تعادلی برای بافر به صورت زیر است:
$$\mathrm { HA } \rightleftharpoons \mathrm { H } ^ { + } + \mathrm { A } ^ { - }$$
قدرت یک اسید ضعیف را به طور معمول به کمک رابطه ثابت تعادل نشان میدهند. ثابت تعادل تفکیک اسید $$K_a$$، که تمایل یک اسید را به تفکیک شدن در یک واکنش نشان میدهد و از رابطه زیر بدست میآید:
$$\mathrm { K } _ { \mathrm { a } } = \frac { \left[ \mathrm { H } ^ { + } \right] \left[ \mathrm { A } ^ { - } \right] } { [ \mathrm { HA } ] }$$
در رابطه بالا، هرقدر صورت کسر بزرگتر باشد، تمایل واکنش به تشکیل $$H^+$$ بیشتر و کاهش pH محلول است.
ظرفیت بافر
محلولهای بافر، ظرفیت محدودی برای ثابت نگهداشتن مقدار pH دارند. اگر بیش از اندازه به یک محلول، باز اضافه کنیم، با از بین رفتن تاثیر اسید ضعیف، هیچ فعالیتی برای تثبیت مقدار pH انجام نخواهد شد. در حالت دیگر، اگر مقدار زیادی اسید به محلول اضافه کنیم، باز ضعیف از بین میرود و فعالیت بافر متوقف خواهد شد.
ظرفیت بافر، مقدار اسید یا بازی است که میتوان به حجم مشخصی از یک محلول بافر اضافه کرد قبل از اینکه pH تغییر محسوسی داشته باشد. ظرفیت یک بافر به مقدار اسید ضعیف و باز مزدوج آن بستگی دارد. به طور مثال، ۱ لیتر از محلول شامل استیک اسید و سدیم استات ۱ مولار، ظرفیت بافر بیشتری از یک لیتر محلول استیک اسید و سدیم استات 0/1 مولار دارد. حتی با اندازهگیری pH نیز متوجه میشویم که مقدار پی اچ برای هر دو محلول یکسان است اما ظرفیت بافر، همانطور که گفته شد، در محلول اول بیشتر است چراکه مقدار بیشتری از استیک اسید و یون استات دارد.
انتخاب محلول بافر مناسب
به طور کلی، دو قانون سرانگشتی برای انتخاب محلول بافر وجود دارد:
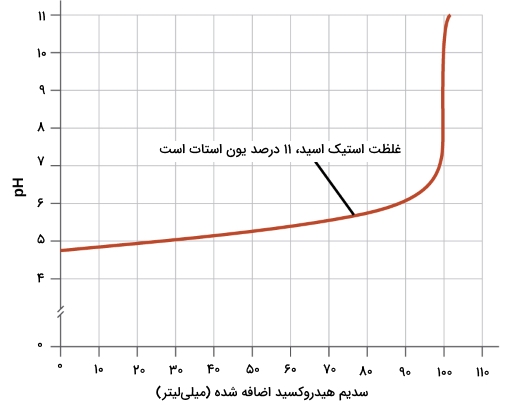
- یک محلول بافر خوب باید غلظتهایی برابر از هر دو جزء داشته باشد. اگر در یک محلول بافر، مقدار یکی از اجزا، کمتر از ۱۰ درصد جزء دیگر باشد، آن محلول کارایی نخواهد داشت. در نمودار زیر، یک باز به محلول بافر شامل استیک اسید و یون استات اضافه میشود. pH اولیه برابر با 4/74 است. زمانی که غلظت استیک اسید به ۱۱ درصد غلظت یون استات در محلول کاهش پیدا میکند، تغییر pH برابر با یک واحد را مشاهده خواهیم کرد.
- اسیدهای ضعیف و نمکهای آنها بافرهای بهتری برای pH کمتر از ۷ هستند و به همین شکل، بازهای ضعیف و نمکهایشان برای pH بالاتر از ۷ مناسباند.
یک نمونه مهم از محلولهای بافر، خون است که در آن کربنیک اسید $$(H_2CO_3)$$ و یون بیکربنات $$(HCO_3 ^ -)$$ نقش اسید و نمک را دارند. زمانی که مقداری اضافی یون هیدروژن به جریان خون وارد شود، این یون به کمک واکنش زیر حذف خواهد شد:
$$\mathrm { H } _ { 3 } \mathrm { O } ^ { + } ( a q ) + \mathrm { HCO } _ { 3 } ^ { - } ( a q ) \longrightarrow \mathrm { H } _ { 2 } \mathrm { CO } _ { 3 } ( a q ) + \mathrm { H } _ { 2 } \mathrm { O } ( l )$$
زمانی هم که مقدار اضافی یون هیدروکسید داشته باشیم، به کمک واکنش زیر حذف خواهد شد:
$$\mathrm { OH } ^ { - } ( a q ) + \mathrm { H } _ { 2 } \mathrm { CO } _ { 3 } ( a q ) \longrightarrow \mathrm { HCO } _ { 3 } ^ { - } ( a q ) + \mathrm { H } _ { 2 } \mathrm { O } ( l )$$
در نتیجه، میزان pH خون در نزدیکی محدوده 7/35 ثابت باقی میماند که نشان از بازی بودن آن دارد. تغییرات pH در خون به طور معمول در حدود 0/1 است و تغییری به میزان 0/4، کشنده خواهد بود.
مثال
غلظت کربنیک اسید خون در حدود ۰/۰۰۱۲ مولار و غلظت یون هیدروژن کربنات 0/024 مولار است. اگر میزان ثابت تفکیک اسید برای کربنیک اسید در دمای بدن، برابر با 6/4 باشد، با استفاده از رابطه هندرسون هاسلبالخ، مقدار pH خون را حساب کنید.
حل: واکنش تعادلی محلول بافر در خون به صورت زیر است:
$$\mathrm { CO } _ { 2 } ( g ) + 2 \mathrm { H } _ { 2 } \mathrm { O } ( l ) \rightleftharpoons \mathrm { H } _ { 2 } \mathrm { CO } _ { 3 } ( a q ) \rightleftharpoons \mathrm { HCO } _ { 3 } ^ { - } ( a q ) + \mathrm { H } _ { 3 } \mathrm { O } ^ { + } ( a q )$$
در نتیجه با استفاده از رابطه هندرسون هاسلبالخ خواهیم داشت:
$$\mathrm { pH } = \mathrm { p } K _ { \mathrm { a } } + \log \frac { [ \mathrm { base } ] } { [ \mathrm { acid } ] } = 6.4 + \log \frac { 0.024 } { 0.0012 } = 7.7$$
در خصوص مثال بالا، ذکر این نکته ضروری است که غلظت کربنیک اسید بسیار کمتر از یون بیکربنات است و دلیل این عدم توازن بین غلظتها، تولید «فرآوردههای فرعی» (by-Product) توسط متابولیسم بدن انسان است. در نتیجه، خون باید حالتی بازی داشته باشد تا از این طریق، ظرفیت بافر افزایش پیدا کند.

کاربرد بافرها
خوب است بدانید، زمانی که ورزش میکنیم، در عضلات ما لاکتیک اسید تولید میشود. زمانی که لاکتیک اسید وارد جریان خون شود، توسط یون بیکربنات خنثی و موجب تولید کربنیک اسید $$(H_2CO_3)$$ خواهد شد. بعد از این مرحله، وجود یک آنزیم کمک میکند تا کربنیک اسید به دیاکسید کربن و آب شکسته و از طریق تنفس خارج شود. درحقیقت، علاوه بر اثرات محلول بافر در خون، تنفس نیز به تنظیم pH خون کمک میکند.
اگر pH خون به میزان زیادی کاهش پیدا کند، افزایش تنفس، $$C O _ 2$$ را به کمک ریهها از خون حذف میکند و با توجه به واکنش حاکم، غلظت $$[ H _ 3 O ^ +]$$ کاهش مییابد. اگر خون، بیش از حد، خاصیتی بازی پیدا کند، تنفس با سرعت آهستهتر موجب کاهش غلظت دیاکسید کربن در خون میشود و واکنش را به طرف افزایش غلظت $$[H ^ +]$$ پیش میبرد.
همانطور که گفته شد، در صنعت از محلولهای بافر به منظور فرآیندهای تخمیری و تنظیم شرایط صحیح رنگها در نساجی بهره میگیرند. همچنین در تیتراسیونهای اسید و باز و کالیبره کردن pHسنجها از محلولهای بافر استفاده میکنند.
محلولهای بافر پر کاربرد
اگر موادی را با یکدیگر ترکیب کنیم که $$pK_a$$ مختلفی داشته باشند و این اختلاف در حد ۲ تا ۳ واحد باشد، با تنظیم pH، بافرهای مختلفی را بدست خواهیم آورد. سیتریک اسید، ترکیب شیمیایی مناسبی برای این کار است چراکه ۳ $$pK_a$$ مختلف دارد و اختلاف مقادیر آن کمتر از دو واحد است. با اضافه کردن سایر «عوامل بافری» (Buffering Agents)، دامنه تغییرات بافر را میتوان گستردهتر کرد. جدول زیر حاوی بافرهایی برای pH از 3 تا ۸ است:
| سیتریک اسید 0/1 مولار (میلیلیتر) | $$(Na_2HPO_4)$$ 0/2 مولار (میلیلیتر) | pH |
| 79/45 | 20/55 | 3 |
| 61/45 | 38/55 | 4 |
| 48/50 | 51/50 | 5 |
| 36/85 | 63/15 | 6 |
| 17/65 | 82/35 | 7 |
| 2/75 | 97/25 | 8 |
لازم به ذکر است، ترکیبی شامل سیتریک اسید، «مونو پتاسیم فسفات» $$(K H _ 2 PO_4)$$، «بوریک اسید» $$(H _ 3 B O _ 3)$$ و «باربیتوریک اسید» $$(C_4H_4N_2O_3)$$، محلول بافری بدست میدهد که میتواند pH از 2/6 تا 12 را پوشش دهد.
جداول ICE جهت محاسبه pH بافر
جداول ICE، حالتهای «اولیه» (Initial)، «تغییر» (Change) و «تعادل» (Equilibrium) را برای واکنشهای برگشتپذیر شامل میشوند که در نهایت موجب سادگی محاسبات خواهند شد.
محاسبه برای اسیدهای تک پروتونه
برای محاسبه pH بافر برای اسیدهای تکپروتونه، ابتدا واکنش تعادلی مربوط به آن را بنویسید:
$$\mathrm { HA } \rightleftharpoons \mathrm { H } ^ { + } + \mathrm { A } ^ { - }$$
این معادله نشان میدهد زمانی که یک اسید، تفکیک میشود، مقادیر مساوی از یون هیدروژن و آنیون به تولید میرسند. غلظتهای تعادلی این جزء را میتوان به کمک جدول ICE محاسبه کرد. در زیر، جدول ICE برای اسید تک پروتونه آورده شده است:
| $$[H^ +]$$ | $$[A ^ -]$$ | $$[HA]$$ | |
| $$y$$ | $$0$$ | $$C_0$$ | I |
| $$x$$ | $$x$$ | $$-x$$ | C |
| $$x+y$$ | $$x$$ | $$C_0-x$$ | E |
در ردیف اول که با حرف I مشخص شده است، شرایط اولیه فهرست شده است: غلظت اسید را با $$C_0$$ نشان میدهیم و از آنجایی که در حالت اولیه، این اسید هنوز تفکیک نشده است، غلظتهای $$A^-$$ و $$H^+$$ صفر خواهند بود. $$y$$ غلظت اولیه اسید قوی اضافه شده به محلول را همچون هیدروکلریک اسید نشان میدهد. اگر یک باز قوی مانند سدیم هیدروکسید به محلول اضافه شود، علامت $$y$$ را منفی در نظر میگیریم چراکه باز سبب حذف یونهای هیدروژن از محلول میشود.
ردیف دوم که با حرف C نشان داده شده است، تغییرات را به هنگام تفکیک اسید مشخص میکند. غلظت اسید با مقدار $$-x$$ کاهش پیدا میکند و غلظتهای $$A^-$$ و $$H^+$$، هر دو با مقدار $$+x$$ افزایش مییابند.
ردیف سوم را با حرف E نشان میدهیم که غلظتهای تعادلی را نشان میدهد. این ردیف شامل مجموع ردیفهای اول و دوم است. برای پیدا کردن عدد $$x$$، باید از رابطه ثابت تعادل استفاده کنیم:
$$K _ { \mathrm { a } } = \frac { \left[ \mathrm { H } ^ { + } \right] \left[ \mathrm { A } ^ { - } \right] } { [ \mathrm { HA } ] }$$
عبارت غلظت را با مقادیر ردیف سوم در جدول ICE جایگزین کنید:
$$K _ { \mathrm { a } } = \frac { x ( x + y ) } { C _ { 0 } - x }$$
با سادهسازی معادله خواهیم داشت:
$$x ^ { 2 } + \left( K _ { \mathrm { a } } + y \right) x - K _ { \mathrm { a } } C _ { 0 } = 0$$
با مقادیر مشخص از $$(K_a)$$، $$(C_0)$$ و $$y$$ میتوان این معادله را برای $$x$$ حل کرد و با استفاده از رابطه pH، میتوان pH بافر را حساب کرد:
$$\mathrm { pH } = - \log _ { 10 } \left[ \mathrm { H } ^ { + } \right]$$
$$\mathrm { pH } = - \log _ { 10 } ( x + y )$$

محاسبه برای اسیدهای چند پروتونه
اسیدهای چند پروتونه از جمله اسیدهایی هستند که بیش از یک پروتون از دست میدهند. ثابت تعادل برای تفکیک اولین پروتون را با $$k _ {a1}$$ نشان میدهند و به همین ترتیب نیز میتوان ثابتهای تعادل دیگری تعریف کرد. سیتریک اسید را میتوان به صورت $$H_3 A$$ نشان داد که یک اسید چندپروتونه است و میتواند سه پروتون از دست بدهد. واکنشهای آن در زیر آورده شدهاند:
$$\mathrm { H } _ { 3 } \mathrm { A } \rightleftharpoons \mathrm { H } _ { 2 } \mathrm { A } ^ { - } + \mathrm { H } ^ { + } \quad \mathrm { p } K _ { \mathrm { a } 1 } = 3.13$$
$$\mathrm { H } _ { 2 } \mathrm { A } ^ { - } \rightleftharpoons \mathrm { HA } ^ { 2 - } + \mathrm { H } ^ { + } \mathrm { p } K _ { \mathrm { a } 2 } = 4.76$$
$$\mathrm { HA } ^ { 2 - } \rightleftharpoons \mathrm { A } ^ { 3 - } + \mathrm { H } ^ { + } \quad \mathrm { p } K _ { \mathrm { a } 3 } = 6.40$$
زمانی که اختلاف مقدار $$pK_a$$ در اسیدهای چندپروتونه، کمتر از ۳ باشد، بین مقادیر pH محلول تعادلی، همپوشانی بوجود میآید و هر قدر این اختلاف کمتر باشد، همپوشانی بیشتر خواهد بود. در خصوص سیتریک اسید، این همپوشانی گسترده است و محلولهای شامل سیتریک اسید، محلولهای بافری با مقدار pH از 2/5 تا 7/5 هستند.
محاسبات pH برای اسیدهای چندپروتونه نیاز به حل دستهای از معادلات غیرخطی موازنه جرم دارد که در خصوص سیتریک اسید، این معادلات شامل حل دو معادله موازنه جرم زیر خواهد بود:
$$\begin{array} { l } { C _ { \mathrm { A } } = \left[ \mathrm { A } ^ { 3 - } \right] + \beta _ { 1 } \left[ \mathrm { A } ^ { 3 - } \right] \left[ \mathrm { H } ^ { + } \right] + \beta _ { 2 } \left[ \mathrm { A } ^ { 3 - } \right] \left[ \mathrm { H } ^ { + } \right] ^ { 2 } + \beta _ { 3 } \left[ \mathrm { A } ^ { 3 - } \right] \left[ \mathrm { H } ^ { + } \right] ^ { 3 } } \ { C _ { \mathrm { H } } = \left[ \mathrm { H } ^ { + } \right] + \beta _ { 1 } \left[ \mathrm { A } ^ { 3 - } \right] \left[ \mathrm { H } ^ { + } \right] + 2 \beta _ { 2 } \left[ \mathrm { A } ^ { 3 - } \right] \left[ \mathrm { H } ^ { + } \right] ^ { 2 } + 3 \beta _ { 3 } \left[ \mathrm { A } ^ { 3 - } \right] \left[ \mathrm { H } ^ { + } \right] ^ { 3 } - K _ { \mathrm { w } } \left[ \mathrm { H } ^ { + } \right] ^ { - 1 } } \end{array}$$
در رابطه بالا:
- $$C_A$$: غلظت تحلیلی اسید
- $$C_H$$: غلظت تحلیلی یون هیدوژن اضافه شده
- $$\beta$$: «ثابت تجمعی» (Cumulative Association Constant) که از روابط زیر بدست میآیند:
$$\log \beta _ { 1 } = \mathrm { p } K _ { \mathrm { a } _ { 3 } } \, \quad \log \beta _ { 2 } = \mathrm { p } K _ { \mathrm { a } _ { 2 } } + \mathrm { p } K _ { \mathrm { a } _ { 3 } } \, \quad \log \beta _ { 3 } = \mathrm { p } K _ { \mathrm { a } _ { 1 } } + \mathrm { p } K _ { \mathrm { a } _ { 2 } } + \mathrm { p } K _ { \mathrm { a } _ { 3 } }$$
- $$K_w$$: ثابت یونش خودبهخودی (خودیونش) آب
برای حل معادله بالا، یک دستگاه معادلات غیر خطی با دو مجهول $$[A ^ {3-}]$$ و $$[H ^ {+}]$$ داریم که بسیاری از برنامههای کامپیوتری قادر به حل آن هستند.
مثال ۱
غلظت $$A^-$$ را برای واکنش زیر پیدا کنید. غلظت اولیه اسید نیز برابر با 0/15 مولار است.
$$HA_{(aq)} + H_2O_{(l)} \rightleftharpoons A^-_{(aq) }+ H_3O_{(aq)}$$
$$[HA (aq)]_{initial} = 0.150 M$$
$$K_a = 1.6 \times 10^{-2}$$
واکنش بالا، واکنش یک اسید ضعیف محلول در آب است. اسید $$HA$$ به باز مزدوج خود $$A^-$$ و پروتون $$H_3O^+$$ تفکیک میشود.
برای حل، جدول را به شکلی که توضیح داده شد تشکیل میدهیم:
| $$[H_3O^+]$$ | $$[A ^ -]$$ | $$[HA]$$ | |
| $$0.00 M$$ | $$0.00 M$$ | $$0.15 M$$ | I |
| $$+xM$$ | $$+xM$$ | $$-x M$$ | C |
| $$xM$$ | $$xM$$ | $$0.0150 - x M$$ | E |
در نهایت، معادله را برای $$K_a$$ بازنویسی میکنیم:
$$K_a = \dfrac{x^2}{0.150-x} = 1.6 \times 10^{-2}$$
برای پیدا کردن غلظت $$x$$، معادله را برای $$x$$ مینویسیم و حل میکنیم:
$$\begin{eqnarray} (1.6 \times 10^{-2})({0.150-x}) &\;=&\; {x^2} \ x^2+(1.6 \times 10^{-2})x-(0.150)(1.6 \times 10^{-2}) &\;=&\; 0 \end{eqnarray}$$
معادله بالا، یک معادله درجه ۲ است. برای حل معادله درجه ۲ به صورت زیر عمل میکنیم:
$$Ax^{2}+Bx+C=0$$
- $$A = 1$$
- $$B = 1.6 \times 10^{-2}$$
- $$C =( -0.150)( 1.6 \times 10^{-2}) = -2.4 \times 10^{-3}$$
با استفاده از فرمولهای زیر، میتوانیم جواب را محاسبه کنیم:
$$x = \dfrac{-B+sqrt{B^2-4AC}}{2A}$$
$$x = \dfrac{-B-sqrt{B^2-4AC}}{2A}$$
در معادلات بالا، هرکدام که به جواب منفی رسید را حذف میکنیم. مقادیر محاسبه شده $$x$$ را میتوان برای محاسبه غلظتهای تعادلی هر فراورده حساب کرد. کافی است که از آن در ردیف E جدول ICE استفاده کنیم.

شرایط نگهداری محلول بافر
به هنگام استفاده از محلولهای بافر، باید آنها را در شرایط مناسبی نگهداری کرد. عمر معمول برای یک محلول بافر تجاری در حدود ۲ سال است. البته بعد از باز کردن ظرف محلول، تنها ۳ تا ۶ ماه میتوان از محلول بافر استفاده کرد. در نتیجه، همین زمان را باید برای محلولهای بافری که در آزمایشگاه تولید میشوند نیز در نظر گرفت.البته این زمان برای بافرهای قلیایی که pH بالاتر از ۱۰ دارند صدق نمیکند. pH این نوع از محلولهای بافر قلیایی در تماس با دیاکسید کربن هوا تغییر میکند و بهترین زمان نگهداری آنها در حدود یک ماه است.
به هنگام کار با محلولهای بافر، نکات زیر را در نظر بگیرید:
- قبل از استفاده از محلول بافر، حتما تاریخ انقضای آن را چک کنید.
- اگر در حال ساخت یک محلول بافر هستید، تاریخ تولید و انقضا را خودتان بر روی ظرف بنویسید.
- محلول بافر را در یک ظرف بسته پلاستیکی یا در بطری و بالونهای مخصوص نگهداری کنید.
- محلولهای بافر را در دمایی بین 15 تا 25 درجه سانتیگراد نگهداری کنید.
اگر این مطلب برای شما مفید بوده است، آموزشهای زیر نیز به شما پیشنهاد میشوند:
- مجموعه آموزشهای دروس شیمی
- مجموعه آموزشهای مهندسی شیمی
- آموزش محلول سازی در آزمایشگاه
- کتون ها — به زبان ساده
- الکترولیت و هدایت الکتریکی — از صفر تا صد
^^










سلام
من میخوام که یک بافر فسفات 60 میلی مولار با پی هاش 5 تهیه کنم. میشه منو راهنمایی کنید که چطور میتونم این بافر رو تهیه کنم؟
سلام
برای تولید یک محلول که در مرحله آخر KOH را به اون اضافه میکنم و pH رو به 13 میرسونم، یکی از ترکیبات محلول Tris هست ولی نمیدونم که نقشش توی این محلول بافر هست یا نه؟ اگر آره چه زمانی باید به محلول اضافه اش کنم؟
سلام و خدا قوت…
خصوصیت zwitterionic بافرها
چگونه خصوصیتی است ؟
به عنوان مثال اسیدهای آمینه غیر ضروری به دلیل همین خصوصیتی که دارند در جنین ویژگی بافری پیدا کرده اند و میتوانند نقش chealator توکسین داشته باشند.
ممنون میشوم اگر وقت کردید توضیح دهید.
با سلام؛
«یون دوقطبی» (Zwitterion) به مولکولی میگویند که شامل تعداد برابر گروههای عاملی با بار مثبت و منفی باشد که آمینواسیدها نیز چنین ویژگی دارند. محلول بافری که جزء اسید یا باز آن نیز یک یون دوقطبی باشد، به آن محلول بافر با یون دوقطبی میگویند.
با تشکر از همراهی شما با مجله فرادرس
سلام
ایا از محلول بافری میتوان بعنوان یه محلول الکترولیت استفاده کرد یا خیر؟مثلا ترکیب مشخصی از خون رو با محلول خاصی برایه ثابت نگه داشتن خواص خون استفاده کرد و در عین حال یک محلول الکترولیت هم داشته باشیم
با سلام؛
بحث در خصوص استفاده از هدایت الکتریکی محلولهای بافری همچنان در حال بررسی است و به تازگی مقالاتی در این خصوص ارائه شده است. علاوه بر این، برای آشنایی با محلولهای الکترولیت نیز میتوانید مطلب «الکترولیت و هدایت الکتریکی — از صفر تا صد» را مطالعه کنید.
از همراهی شما با مجله فرادرس سپاسگزاریم.
سلام مرسی از متنتون خیلی مفید بود ولی یه سوالی که دارم اینه که pkaسیستم بی کربنات حدود ۲.۳۴ و ۱۰.۲ هستش این در حالیه که phخون حدودا بین ۶.۹ تا ۷.۴ هستش اگر اشتباه نکنم پس این سیستم بافری چطوری میتونه توی خون خاصیت بافری داشته باشه با این که اصلا phخون در محدوده بافری اون قرار نمیگیره؟
با سلام
دلیل استفاده از بافر آمونیاکی ph=10 در آزمایش تیتراسیون کمپلکسومتری چیست ؟
بسم الله
با سلام .
در صورت این مثال غلظت ها را اشتباه وارد کردین. چون در حل از مقادیر متفاوتی استفاده نمودید
غلظت کربنیک اسید خون در حدود 0/012 مولار و غلظت یون هیدروژن کربنات 0/024 مولار است. اگر میزان ثابت تفکیک اسید برای کربنیک اسید در دمای بدن، برابر با 6/4 باشد، با استفاده از رابطه هندرسون هاسلبالخ، مقدار pH خون را حساب کنید.
یا علی ع
با سلام؛
از شما بابت بیان مشکل سپاسگزاریم. در سوال میزان غلظت کربنیک اسید خون به جای ۰/۰۰۱۲ مولار، ۰/۰۱۲ ذکر شده بود که اصلاح شد. باقی موارد صحیح هستند.
با تشکر
سلام وقتتون بخیر.به زبان ساده واسه منی ک شیمی زیاد نمیدونم درحد دبیرستان.رشته ی داشنگاهیمم مهندسی عمران بودش ک اصلا شیمی نداشت.چجوری میتونم محلول کاهش و افزایش پی اچ درست کنم؟ک باهاش بتونم پی اچ اب یا هرمحلول دیگه رو بااضافه کردن چندقطره پایین بیارم؟با پی اچ متر اندازه بگیرم و بامحلول افزایش بالا ببرم و یا با محلول کاهش پایین بیارم.
با سلام؛
از شما به دلیل مطالعه این مطلب، سپاسگزاریم.
به طور کلی برای افزایش یا کاهش pH یک محلول میتوانید به ترتیب از محلولهای سدیم هیدروکسید یا هیدروکلریک اسید استفاده کنید. البته برای درک بهتر این واکنشها و همچنین آشنایی با محاسبات اسید و باز، مطالعه مطالب زیر را پیشنهاد میکنیم. برای اضافه کردن محلول نیز از یک بورت کمک بگیرید.
pH چیست؟ — به زبان ساده
واکنش خنثی شدن در شیمی — به زبان ساده
تیتراسیون — به زبان ساده
با تشکر
سلام
ممنون از مطالب مفیدتان
یه سوال داشتم … اگر بافری را با آب رقیق کنیم قدرت بافری آن تغییر میکند؟ پی اچ آن چطور؟
با سلام؛
از همراهی شما با مجله فرادرس سپاسگزاریم. برای توصیف دقیق این مفهوم باید به معادله هندرسون هاسلباخ مراجعه کنیم:
$$\begin{equation}\mathrm{pH}=\mathrm{pKa}+\log \left(\frac{\left[A^{-}\right]}{[H A]}\right)\end{equation}$$
اگر با دقت به این معادله نگاه کنیم، متوجه میشویم که رقیق کردن محلول بافری، میزان pH آنرا تغییر نمیدهد چراکه به هنگام رقیق کردن، غلظتهای $$\left[A^{-}\right]$$ و $${[H A]}$$ به یک میزان تغییر میکنند و بنابراین، این نسبت ثابت میماند.
اما آنچیزی که در واقعیت اتفاق میافتد این است که میزان pH به هنگام رقیقسازی تغییر پیدا میکند اما این تغییر زیاد نیست. در حقیقت، این تغییر در مقایسه با اضافه کردن محلول رقیق اسید و باز قوی، ناچیز است. برای بررسی این علت، بار دیگر به معادله هندرسون-هاسلباخ مراجعه میکنیم. این رابطه نوعی تقریب است، به طور مثال، زمانیکه به محاسبه pH میپردازید ممکن است به عبارت زیر برخورد کنید:
$$(0.1 – x)$$
در توضیح معادلات تعادلی، عبارت $$x$$ در مقایسه با عدد $$0.1$$، بسیار کوچک و قابل صرف نظر است و به هنگام محاسبات، برای سادهسازی میتوان از این عدد صرف نظر کرد. اما زمانی که یک محلول بافر را رقیق میکنیم، نمیتوان از عبارات $${[H A]} – x$$ و $$\left[A^{-}\right] + x$$ صرفنظر کرد چراکه در این حالت، مقدار عبارت $$x$$ در مقایسه با سایر عبارات، قابل چشمپوشی نیست.
البته این مورد به یکباره اتفاق نمیافتد بلکه رابطه هندرسون-هاسلباخ، خطای بسیار کمی دارد و با رقیق کردن محلول بافر، حتی ممکن است تغییری رخ ندهد اما در نقطهای، با رقیق کردن محلول، این تغییرات اتفاق میافتند. برای بررسی تغییر ظرفیت بافر نیز میتوان از همین دلایل استفاده کرد اما پیشنهاد میکنیم بار دیگر بخشهای ظرفیت بافر و انتخاب محلول بافر مناسب را مطالعه کنید.
با تشکر
سلام و خسته نباشید و ممنون از مطالب مفیدتون ببخشید یه سوال داشتم و اون هم کار کردن با فرمول بتا هست که میشه تغییر غلظت به تغییر ph آیا مسئله ای مربوط به این فرمول میتونین مثال بزنین تا کار با اون رو بهتر بفهمم
سلام من یه سوال داشتم اینکه چرا phمحلول بافر در اثر رقیق کردن تغییر نمیکند؟
با سلام؛
از توجه شما سپاسگزاریم. در حقیقت، همانطور که در متن هم به آن اشاره شد، یک سیستم بافری، اثر باز یا اسید اضافه شده را تا حدی خنثی میکند که نمونه آن نیز، سیستم بافری خون است که واکنشهای آن در بخش «انتخاب محلول بافر مناسب» آورده شده است. پیشنهاد میکنم این بخش را یک بار دیگر مطالعه و واکنشهای آن را بررسی کنید.
با تشکر
عرض سلام و تشکر بابت مقاله بسیار مفیدتون. سوالی داشتم در مورد اینکه چطور میشه به یک سیستم بافری غلبه کرد؟ به عنوان مثال نیاز به تغییر pH در یک محلول هست که خواص بافری دارد. چگونه می توان با صرف کمترین میزان اسید یا باز مصرفی pH را به سرعت تغییر داد؟ با تشکر
با سلام؛
از حسن توجه شما سپاسگزاریم. در حقیقت، پاسخ سوال شما به طور کامل با مفهوم تیتراسیون مرتبط است چراکه در تیتراسیون و رسم نمودارهای آن، با پیدا کردن نقاط تعادل و پایانی، به خوبی، توانایی یک سیستم بافری مورد سنجش قرار میگیرد. پیشنهاد میکنم برای آشنایی با این مفهوم و انجام محاسبات آن، مطالب زیر را مطالعه کنید:
تیتراسیون — به زبان ساده
تیتراسیون اسید باز — از صفر تا صد
تیتراسیون اکسایش کاهش — از صفر تا صد
با تشکر