مشتق ضمنی — به زبان ساده

در این مطلب قصد داریم روشی متفاوت در مشتق‌گیری تحت عنوان مشتق‌ ضمنی را توضیح دهیم. جهت درک بهتر پیشنهاد می‌شود قبل از مطالعه‌ی این مطلب، مطالب مشتق و روش‌های مشتق‌گیری را مطالعه فرمایید.

ضمنی و صریح

یک تابع می‌تواند در قالب یک عبارت ضمنی یا در قالب عبارتی صریح ارائه شود. توابع و مشتقاتی که با آن‌ها مواجه بوده‌اید، به‌صورت صریح بوده‌اند.

فیلم آموزش ریاضی عمومی 2 – جامع و کاربردی در فرادرس

کلیک کنید

به‌طور خلاصه توابع صریح و ضمنی به‌صورت زیر تعریف می‌شوند.

• عبارات صریح: عبارتی که در آن y مستقیما به‌صورت تابعی از x تعریف می‌شوند.
• عبارات ضمنی: در عبارات ضمنی، تابع y بر حسب خودش و متغیر‌هایش بیان می‌شوند. در این عبارات با معلوم بودن مقدار x نمی‌توان مستقیما مقدار y را محاسبه کرد.

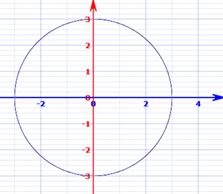
جهت شناسایی عبارات صریح و ضمنی مثال‌هایی زده شده که در ادامه ارائه شده‌اند. برای نمونه معادله دایره را می‌توان مطابق با روابط زیر بیان کرد:

هر دو تابع فوق یک شکل را نمایش می‌دهند، اما در رابطه سمت چپ y مستقیما بر حسب x و در رابطه سمت راست، عبارتی بر حسب y و x بیان شده است.

نحوه محاسبه مشتقِ عبارت ضمنی

جهت محاسبه مشتق زنجیره‌ای، مراحل زیر را انجام دهید:

1. مشتق‌گیری بر حسب x
2. جمع کردن عبارات $$\frac {dy}{dx}$$ در یک سمت
3. حل معادله بدست آمده و پیدا کردن $$\frac {dy}{dx}$$

فیلم آموزش معادلات دیفرانسیل با رویکرد حل مساله و تست کنکور ارشد در فرادرس

کلیک کنید

مثال ۱

در عبارت زیر حاصل $$\frac {dy}{dx}$$ (یا همان 'y) را بیابید.

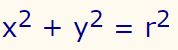
پاسخ: همان‌طور که در بالا نیز بیان شد،‌ در قدم نخست، از کل عبارت بایستی نسبت به x مشتق گرفته شود. با محاسبه مشتق مذکور داریم:

حاصل هریک از مشتق‌های بالا به تفکیک در زیر نوشته شده‌‌اند.

با جایگذاری عبارات بالا در رابطه ۱، خواهیم داشت:

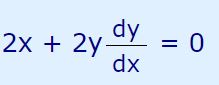
در بالا بیان کردیم که پس از نوشتن مشتق ضمنی، بایستی عبارات $$\frac {dy}{dx}$$ را در یک سمت قرار دهیم. بنابراین رابطه بالا را می‌توان به‌صورت زیر بازنویسی کرد.

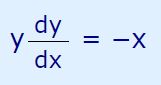
نهایتا با حل عبارت بالا بر حسب $$\frac {dy}{dx}$$، مشتق 'y برابر با رابطه زیر بدست می‌آید.

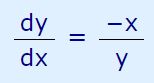
مشتق‌گیری زنجیر‌ه‌ای

شاید این سوال برایتان پیش آمده باشد که در مثال ۱ عبارت $$\frac {dy^2}{dx}$$ چگونه بدست آمده است؟ این عبارت با استفاده از مشتق‌گیری زنجیره‌ای بدست آمده. قانون مشتق‌گیری زنجیره‌ای می‌گوید:

توجه داشته باشید که در رابطه بالا u عبارتی است که می‌تواند شامل x و y باشد. حال فرض کنید می‌خواهیم مشتق تابع y² را نسبت به متغیر x بدست آوریم. برای انجام این کار u=y² در نظر می‌گیریم. رابطه ۲ برای u برابر است با:

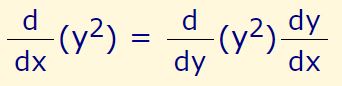
در نتیجه:

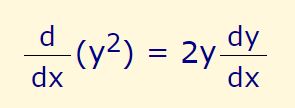
مثال ۲

حاصل مشتق y بر حسب x را در مثال ۱ با استفاده از مشتق‌گیری صریح بدست آورید.

فیلم آموزش معادلات دیفرانسیل + حل سوالات کنکور کارشناسی ارشد در فرادرس

کلیک کنید

پاسخ:‌ رابطه اصلی به‌صورت x²+y²=r² بود. به‌منظور مشتق‌گیری به‌صورت صریح، مراحل زیر را انجام می‌دهیم.

همان‌طور که در بالا می‌بینید، مشتق بدست آمده برابر با پاسخی است که در مثال ۱ بدست آمد. بنابراین هر دو روشِ صریح و ضمنی یک نتیجه را منجر می‌شوند؛ اما این زمان حل است که در این دو متفاوت خواهد بود.

کاربرد روش ضمنی

به‌نظر می‌رسد روش صریح در مشتق‌گیری آسان‌تر باشد؛‌ اما به‌راستی چرا از مشتق‌گیری ضمنی استفاده می‌شود؟ واقعیت این است که در توابع پیچیده و یا توابعی که در آن‌ها از توان‌های چندم y استفاده شده، $$\frac {dy}{dx}$$ یا 'y را راحت‌تر می‌توان بدست آورد. برای نمونه به مثال زیر توجه فرمایید.

فیلم آموزش حل معادلات دیفرانسیل با متمتیکا Mathematica در فرادرس

کلیک کنید

مثال ۳

دایره‌ای به شعاع ۵ را در نظر بگیرید. شیب خط مماس به دایره در نقطه (3,4) را بدست آورید. کافی است نقطه مذکور را در پاسخ بدست آمده در مثال ۱ -یا ۲- قرار دهید. بنابراین شیب به‌دست آمده در نقطه مذکور برابر است با:

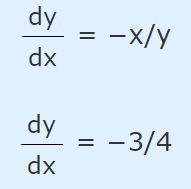
هم‌چنین با توجه به مطلب معادله خط، رابطه خط مماس بدست آمده برابر است با:

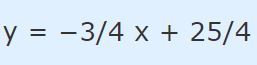
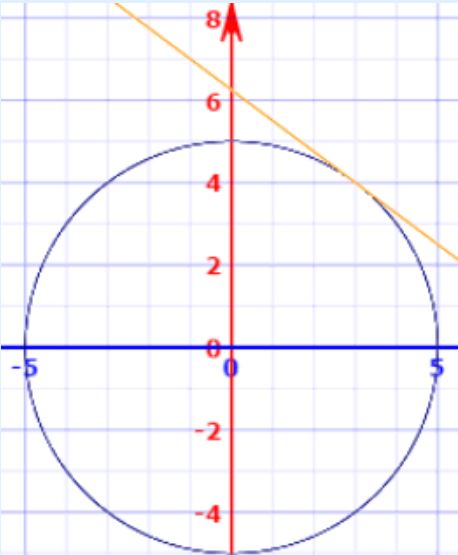
در شکل زیر دایره مذکور و خط مماس بدست آمده بر آن، نشان داده شده‌اند.

در بعضی از موارد مشتق‌گیری صریح از y تقریبا غیر ممکن به‌نظر می‌رسد. در چنین مواردی بهتر است از مشتق‌گیری ضمنی استفاده شود. برای نمونه در مثال ۴ عبارتی پیچیده نسبت به y ارائه شده که در آن مشتق‌گیری به‌صورت ضمنی و در زمانی کوتاه انجام شده است.

مثال ۴

$$\frac {dy}{dx}$$ را در عبارت 10x⁴-18xy²+10y³=48 بیابید.

پاسخ: قدم‌های بیان شده در بالا را به‌ یاد دارید؟

• مشتق‌گیری از کل عبارت نسبت به x
• انتقال عبارات $$\frac {dy}{dx}$$ به یک سمت
• حل عبارت بدست آمده بر حسب $$\frac {dy}{dx}$$

در ادامه، این مراحل نشان داده شده‌اند.

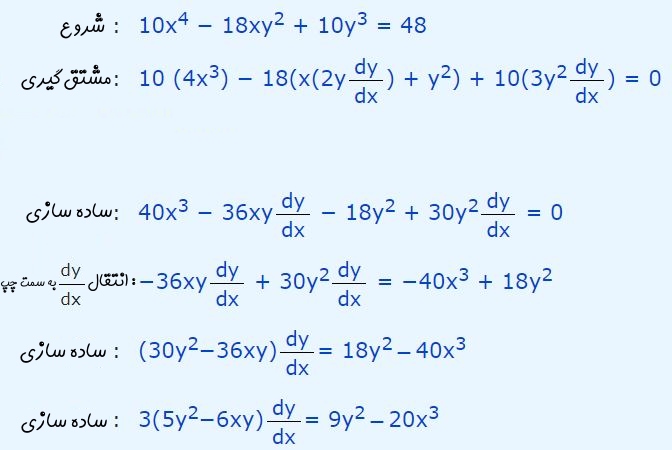
عبارت بدست آمده در بالا، رابطه‌ای را نشان می‌دهد که در آن $$\frac {dy}{dx}$$ نیز موجود است. با حل رابطه فوق داریم:

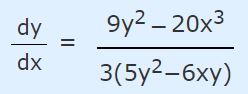
در مثال‌های ارائه شده ممکن است از قوانینی استفاده شده باشد، که برای شما آشنا نباشد. در این صورت می‌توانید با مطالعه مطلب روش‌های مشتق‌گیری با روش‌های مذکور آشنا شوید.

مشتق‌گیری از توابع معکوس

روش مشتق‌گیری ضمنی روشی پرکاربرد در محاسبه مشتق توابع معکوس است. در مواردی که هدف ما محاسبه مشتق توابع معکوس است، در ابتدا تابع را از حالت معکوس خارج کرده و از طرفین آن به‌صورت ضمنی مشتق می‌گیریم.

فیلم آموزش ریاضی عمومی ۱ + حل مثال و تست کنکور کارشناسی ارشد در فرادرس

کلیک کنید

مثال ۵

مشتق تابع معکوسِ y=sin^-1x را بیابید.

پاسخ: همان‌طور که در بالا نیز بیان شد در ابتدا بایستی تابع را از حالت معکوس خارج کرده و از آن‌ مشتق بگیریم. در حقیقت می‌توان گفت:

حال از طرفین رابطه فوق به‌صورت ضمنی مشتق می‌گیریم.

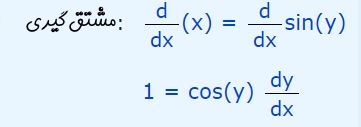
رابطه فوق را می‌توان به‌صورت زیر، بر حسب $$\frac {dy}{dx}$$ نوشت.

عملاً مشتق y بر حسب x بدست آمده. اما پاسخ این مسئله را می‌توان یک گام بیشتر نیز به جلو برد. در حقیقت کامل‌ترین پاسخ زمانی است که 'y بر حسب فقط x بیان شود. برای انجام این کار در ابتدا می‌توان رابطه زیر را نوشت:

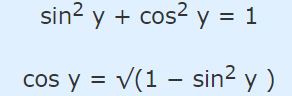
با توجه به این‌که sin y=x است؛ در نتیجه می‌توان این عبارت را در رابطه بالا نیز اعمال کرد. با انجام این کار به رابطه زیر می‌رسیم.

با بدست آمدن cos y، حاصل مشتق y نسبت به x نیز برابر می‌شود با:

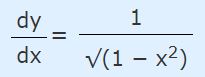
در حالت کلی می‌توان با اندکی خلاقیت حاصل مشتق بسیاری از توابع را با استفاده از روش مشتق‌گیری ضمنی بدست آورد.

مثال ۶

حاصل $$\frac {dy}{dx}$$ را در تابع $$y=\sqrt{x}$$ با استفاده از مشتق‌گیری ضمنی بدست آورید.

فیلم آموزش ریاضی عمومی ۲ – مرور و حل تمرین در فرادرس

کلیک کنید

پاسخ: جهت مشتق‌گیری ضمنی و برای راحت‌تر شدن حل مسئله می‌توان عبارت را به نحوی بیان کرد که در آن رادیکال وجود نداشته باشد. در حقیقت تابع مذکور به‌صورت زیر نیز قابل بازنویسی است:

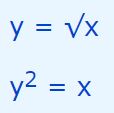
حال از طرفین این رابطه به‌صورت ضمنی، نسبت به x مشتق می‌گیریم.

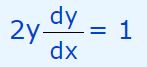
با ساده سازی، $$\frac {dy}{dx}$$ برابر با عبارت زیر بدست می‌آید.

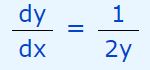
از صورت سوال می‌دانیم که تابع $$y=\sqrt{x}$$ است. با جایگذاری y در رابطه بالا، حاصل مشتق برابر می‌شود با:

در مطلب روش‌های مشتق‌گیری همین پاسخ را با استفاده از قانون توانی بدست آوردیم.

خلاصه

• جهت محاسبه مشتق یک عبارت ضمنی:

1. از عبارتِ ضمنی نسبت به x مشتق بگیرید.
2. عبارات $$\frac {dy}{dx}$$ را در یک سمت قرار دهید.
3. عبارت بدست آمده را بر حسب $$\frac {dy}{dx}$$ حل کنید.

• به‌منظور محاسبه مشتق تابع معکوس در ابتدا تابع را از حالت معکوس خارج کرده و پس از آن مراحل ۱ تا ۳ ارائه شده در بالا را انجام دهید.