محاسبات کوانتومی چیست و چه کاربردی دارد؟ – به زبان ساده

صد سال قبل و درست زمانی که تصور می‌شد علم فیزیک به پایان راه خود رسیده است، انقلابی در این شاخه از علم به پاشد. ظهور فیزیک کوانتوم خط بطلانی بر این باور کشید و راهی نوین را پیش روی فیزیک‌دان‌ها باز کرد. فیزیک کوانتوم رفتار ذرات را در مقیاس اتمی و بسیار کوچک بررسی می‌کند. ۸۰ سال پس از ظهور فیزیک کوانتوم، پژوهشگران به این نتیجه رسیدند که می‌توانند با استفاده از کوانتوم و علوم کامپیوتری، مسائل بسیار پیچیده‌ای را حل کنند. در این مطلب از مجله فرادرس سعی می‌کنیم ابتدا به پرسش محاسبات کوانتومی چیست به زبان ساده پاسخ دهیم.

در ادامه، در مورد مفاهیم موردنیاز در محاسبات کوانتومی مانند کیوبیت، برهم‌نهی کوانتومی، درهم‌تنیدگی کوانتومی، ناهمدوسی و الگوریتم‌های کوانتومی صحبت می‌کنیم. الگوریتم‌ها کوانتومی بسیاری در محاسبات کوانتومی وجود دارند که در این مطلب، «الگوریتم شور» (Shor's Algorithm) را توضیح می‌دهیم. در پایان، با مهم‌ترین مزایای کامپیوترهای کوانتومی، در کنار محدودیت‌های آن‌ها آشنا خواهیم شد.

محاسبات کوانتومی چیست ؟

محاسبات کوانتومی حوزه‌ای از علوم کامپیوتر است که بر توسعه فناوری‌های مختلف با استفاده از فیزیک کوانتوم تمرکز دارد. محاسبات کوانتومی از رفتارهای منحصربه‌فرد فیزیک کوانتوم برای حل مسائلی استفاده می‌کند که کامپیوترهای معمولی از عهده حل آن‌ها برنمی‌آیند. با ساخت کامپیوترهای کوانتومی می‌توان به این دستاورد رسید.

فیلم آموزش محاسبات کوانتومی در فرادرس

کلیک کنید

فرض کنید با دوست خود به کافی‌نت رفته‌اید و آنجا تصمیم می‌گیرید یکی از بازی‌های کامپیوتری، مانند بازی سکه، را بازی کنید. به جای انتخاب دوست خود به عنوان حریف، کامپیوتر را به عنوانی حریفی باهوش‌تر انتخاب می‌کنید. کامپیوتر، همانند انسان، می‌تواند سکه‌ها را حرکت دهد. همان‌طور که می‌دانیم سکه دو سمت دارد، پشت و رو. بازی با سکه‌ای که به سمت رو قرار گرفته است، آغاز می‌شود. کامپیوتر به عنوان حریف، بازی را آغاز می‌کند و دو انتخاب دارد:

1. سکه را پرتاب کند.
2. سکه را پرتاب نکند.

اما شما نمی‌توانید نتیجه نهایی را مشاهده کنید. نوبت شما فرا می‌رسد. شما نیز دو انتخاب دارید، سکه را پرتاب می‌کنید یا پرتاب نمی‌کنید. به طور مشابه، حرکت شما نیز به کامپیوتر نشان داده نمی‌شود. پس از شما، بار دیگر نوبت به کامپیوتر می‌رسد و مشابه بار اول می‌تواند سکه را پرتاب کند یا پرتاب نکند. پس از آن، سکه نشان داده می‌شود:

• اگر سکه به سمت رو باشد، کامپیوتر پیروز می‌شود.
• اگر سکه به سمت پشت باشد، شما پیروز می‌شوید.

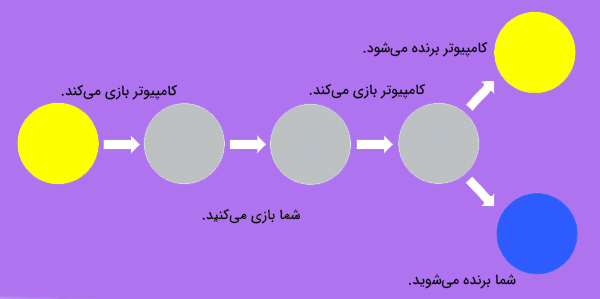
مسابقه فوق بسیار ساده است. اگر طرفین صادقانه بازی کنند و سکه سالم باشد، با احتمال ۵۰ درصد در این مسابقه برنده خواهید شد. اگر به جای کامپیوتر معمولی، بتوانید این مسابقه را با کامپیوتر کوانتومی انجام دهید، چه اتفاقی رخ می‌دهد؟ دسترسی به کامپیوتر کوانتومی راحت نیست و برخی از شرکت‌های بزرگ در سراسر دنیا، مانند شرکت IMB در آمریکا، موفق به ساخت آن شده‌اند. سوالی که ممکن است مطرح شود آن است که کامپیوتر کوانتومی چیست. فیزیک کوانتوم، رفتار اتم‌ها و ذرات بنیادی مانند فوتون‌ها و الکترون‌ها را توصیف می‌کند.

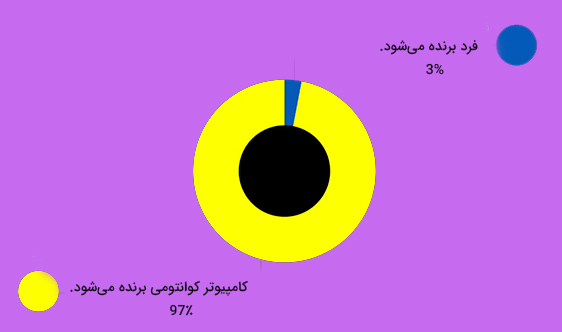
کامپیوتر کوانتومی با کنترل رفتار این ذرات کار می‌کند. عملکرد کامپیوتر کوانتومی به طور کامل با عملکرد کامپیوترهای معمولی تفاوت دارد. کامپیوتر کوانتومی، تنها نسخه قوی‌تری از کامپیوترهای معمولی نیست. کامپیوتر کوانتومی وسیله کاملا جدیدی است که براساس فیزیک کوانتوم کار می‌کند. کامپیوترهای کوانتومی می‌توانند زندگی بشر را در بسیاری از زمینه‌ها، مانند سلامتی و اینترنت، تغییر دهند. شرکت‌های بزرگی در سراسر دنیا به دنبال ساخت این نوع کامپیوتر هستند. در ابتدای مطلب دیدیم اگر بازی سکه را با کامپیوتر معمولی انجام دهیم، با احتمالی نزدیک به ۵۰ درصد کامپیوتر مسابقه را می‌برد یا می‌بازد.

این موضوع بدان معنا است که احتمال پیروزی یا شکست شما در این مسابقه نیز تقریبا برابر ۵۰ درصد خواهد بود. اگر این مسابقه را با کامپیوتر کوانتومی انجام دهید چه اتفاقی می‌افتد؟ کامپیوتر کوانتومی تقریبا و با احتمال ۹۷ درصد پیروز می‌شود. این بدان معنا است که کامپیوتر کوانتومی تقریبا با هر کسی بازی کند، مسابقه را می‌برد. احتمال ۳ درصد باخت آن نیز به دلیل اشتباهات عملکردی در کامپیوتر است.

کامپیوتر کوانتومی چگونه به این دستاورد بزرگ رسیده است؟ فیزیک کوانتوم دلیل اصلی این دستاورد است. کامپیوتر معمولی پشت و روی سکه را به صورت بیت شبیه‌سازی می‌کند، صفر یا یک. پرتاب یا عدم پرتاب سکه نیز به همین صورت شبیه‌سازی می‌شود. عملکرد کامپیوتر کوانتومی کاملا متفاوت است. کامپیوتر کوانتومی دو حالت صفر، یک و ترکیب‌های مختلفی از این دو حالت را دارد. به همین دلیل، احتمال باخت شما در کامپیوتر کوانتومی افزایش می‌یابد. سکه را پرتاب کنید یا پرتاب نکنید، نتیجه کار بین دو حالت صفر و یک وجود خواهد داشت.

کامپیوترهای کوانتومی براساس بیت کوانتومی یا کیوبیت کار می‌کنند. کیوبیت به جای داشتن مقدار صفر یا یک به صورت برهم‌نهی صفر و یک وجود دارد. در واقع، کیوبیت به جای دو مقدار صفر و یک، به صورت طیفی از ترکیب‌های صفر و یک وجود دارد. به عنوان مثال، ممکن است با احتمال ۷۰ درصد، حالت یک و با احتمال ۳۰ درصد، حالت صفر رخ دهد. این اعداد می‌توانند به صورت ۸۰ و ۲۰ یا ۶۰ و ۴۰ نیز تغییر کنند. تعداد این ترکیب‌ها می‌تواند تا بی‌نهایت ادامه داشته باشد. نکته اصلی آن است که باید از مقدارهای دقیق صفر و یک دور شد و عدم قطعیت را پذیرفت.

به هنگام مسابقه، کامپیوتر کوانتومی، ترکیب‌های مختلفی از پشت و رو یا صفر و یک را ایجاد می‌کند. این‌که شما سکه را پرتاب کنید یا نه مهم نیست، برهم‌نهی بدون تغییر باقی می‌ماند. این برهم‌نهی تا حدودی شبیه مخلوط کردن دو سیال با یکدیگر است. دو سیال را به هم بزنید یا نزنید، در مخلوط وجود دارند. اما در آخرین حرکت، کامپیوتر کوانتومی می‌تواند، صفر و یک را از یکدیگر جدا کند. بنابراین، شما هر بار بازی را واگذار می‌کنید.

عملکرد کامپیوتر کوانتومی، برهم‌نهی صفر و یک و عدم قطعیت در نگاه نخست بسیار عجیب به نظر می‌رسند. سکه‌های معمولی به صورت ترکیبی از پشت و رو وجود ندارند. نتیجه پرتاب سکه، یا صفر است یا یک، نه ترکیبی از صفر و یک. پدیده‌های کوانتومی بسیار عجیب و غیر واقعی به نظر می‌رسند، اما اثرات واقعی آن را می‌توانیم در عمل و به عنوان نتیجه بازی در کامپیوتر کوانتومی مشاهده کنیم.

تا اینجا می‌دانیم محاسبات کوانتومی چیست و با کلیات آن آشنا شدیم. به منظور داشتن درک عمیق‌تری از محاسبات کوانتومی باید با مفاهیمی مانند کیوبیت، برهم‌نهی، درهم‌تنیدگی کوانتومی و الگوریتم‌های کوانتومی نیز آشنا شویم. در ادامه، در مورد هر یک از این موضوع‌ها به زبان ساده و به اختصار صحبت می‌کنیم.

کیوبیت در محاسبات کوانتومی چیست ؟

در بخش قبل فهمیدیم محاسبات کوانتومی چیست. این محاسبات در کامپیوترهای کوانتومی انجام می‌شوند. کامپیوترهای معمولی براساس بیت کار و اطلاعات را ذخیره می‌کنند. کیوبیت در اطلاعات کوانتومی و کامپیوترهای کوانتومی همان نقش بیت در کامپیوترهای معمولی را ایفا می‌کند. در این بخش کیوبیت را تعریف و ویژگی‌های آن را با بیت مقایسه می‌کنیم. بیت می‌تواند یک یا صفر باشد. بنابراین، بیت دو حالت دارد.

فیلم آموزش نرم افزار متمتیکا – حل محاسبات کوانتومی با Mathematica در فرادرس

کلیک کنید

کیوبیت نیز همانند بیت می‌تواند حالت‌های مختلفی داشته باشد. در واقع، کیوبیت می‌تواند حالت‌هایی به جز صفر و یک داشته باشد. کیوبیت می‌تواند ترکیب خطی از حالت‌های صفر و یک باشد و به صورت زیر نوشته شود:

$$Qbit = \alpha | 0 > + \beta | 1 > $$

به این حالت برهم‌نهی کوانتومی گفته می‌شود. اعداد $$\alpha$$ و $$ \beta $$ می‌توانند اعداد موهومی باشند. به حالت‌های $$ | 0 > = \left(\begin{array}{c}1\\ 0\end{array}\right) $$ و $$ | 1 > = \left(\begin{array}{c}0\\ 1 \end{array}\right) $$ حالت‌های پایه محاسباتی می‌گوییم. بیت یا در حالت یک قرار دارد یا در حالت صفر. در واقع، بیت با احتمال ۵۰ درصد در حالت صفر و با احتمال ۵۰ درصد در حالت یک قرار دارد. اما این موضوع برای کیوبیت کاملا متفاوت است. برای دانستن حالت کوانتومی کیوبیت باید مقدارهای $$\alpha$$ و $$ \beta $$ را بدانیم. به هنگام اندازه‌گیری کیوبیت، دو نتیجه به‌دست می‌آید:

1. $$| 0 >$$ با احتمال $$\alpha ^ 2 $$
2. $$| 1 >$$ با احتمال $$\beta ^ 2 $$

بنابراین، با انجام یک اندازه‌گیری نمی‌توانیم مقدارهای $$\alpha$$ و $$ \beta $$ را به‌دست آوریم. در حالت کلی، حالت کیوبیت، برداری واحد در فضای برداری پیچیده‌ای است که با انجام اندازه‌گیری به یکی از بردارهای پایه، فروپاشیده می‌شود.

تا اینجا می‌دانیم محاسبات کوانتومی چیست و بیت و کیوبیت چه تفاوتی با یکدیگر دارند. برای داشتن درک بهتری از محاسبات کوانتومی باید با مفاهیمی مانند برهم‌نهی و درهم‌تنیدگی کوانتومی آشنا شویم.

برهم نهی در محاسبات کوانتومی چیست ؟

به طور حتم، هر کسی که فیزیک کوانتوم را مطالعه کرده باشد یا علاقه‌مند به یادگیری آن باشد، این عبارت را شنیده است، الکترون می‌تواند همزمان در حالت‌های متفاوتی قرار داشته باشد. اگر بشنوید این عبارت دروغ است، چه حسی به شما دست می‌دهد؟ ذرات کوانتومی همزمان در حالت‌های متفاوتی قرار ندارند. آن‌ها در زمانی مشخص می‌توانند در یک حالت قرار داشته باشند. ما هیچ حسی به حالت‌های کوانتومی نداریم.

فیلم آموزش مکانیک کوانتومی پیشرفته ۱ در فرادرس

کلیک کنید

برای درک بهتر مفهوم برهم‌نهی به جای صحبت در مورد الکترون و اسپین آن، توپی کوچک را در نظر می‌گیریم. فرض کنید دو توپ، با جنس‌های متفاوت، نرم و زبر، داریم. توپ‌ها در جای خود به صورت ثابت قرار نگرفته‌اند. توپ زبر را می‌توانیم پس از پالیش دادن، نرم یا توپ نرم را با استفاده از زبرکننده، زبر کنیم. بنابراین، اگر بخواهیم می‌توانیم حالت هر یک از توپ‌ها را تغییر دهیم. اما علاقه‌ای به انجام این کار نداریم.

اکنون فرض کنید، این توپ‌ها کوانتومی هستند. حالت سومی را فرض کنید که همزمان زبر و نرم است. به این حالت برهم‌نهی کوانتومی گفت می‌شود. در نگاه نخست این‌گونه به نظر می‌رسد که حالت سوم برابر چندین حالت به صورت همزمان است. اما این‌گونه نیست. توجه به این نکته مهم است که حتی حالت برهم‌نهی کوانتومی، تک حالت است، نه چند حالت متفاوت. این مثال به ما این تصور را می‌دهد که تنها سه حالت وجود دارند. اما در واقعیت، تعداد بی‌شماری حالت داریم. به این نکته توجه داشته باشید که حالت برهم‌نهی کوانتومی، حالت عجیبی نیست، بلکه حالت توپ نرم و توپ زبر، دو حالت عجیب هستند. برای درک بهتر این موضوع، رفتار بردارها را با یکدیگر مرور می‌کنیم.

بردار، کمیتی است که هم اندازه دارد و هم جهت. بردار را می‌توان توسط فلش یا پیکان نشان داد. هر بردار را می‌توان در راستای محورهای $$x$$ و $$y$$ و $$z$$ تجزیه کرد و برحسب بردارهای $$ \widehat{ i } $$ و $$ \widehat{ j } $$ و $$ \widehat{ k } $$ نوشت. به بردارهای $$ \widehat{ i } $$ و $$ \widehat{ j } $$ و $$ \widehat{ k } $$، بردارهای واحد گفته می‌شود. هر برداری در فضای سه‌بعدی را می‌توانیم برحسب این سه بردار واحد بنویسیم. به مجموعه‌ای از بردارها که می‌توانند برحسب بردارهای پایه نوشته شوند، فضای برداری می‌گوییم. فضاهای برداری زیادی وجود دارند. توجه به این نکته مهم است که بردارها تنها، ابزار ریاضی هستند و گاهی می‌توان برای کارهای غیرمنتظره‌ای از آن‌ها استفاده کرد.

در حالت کلی به فضای ساخته شده توسط سه بردار واحد $$ \widehat{ i } $$ و $$ \widehat{ j } $$ و $$ \widehat{ k } $$، فضای مکان می‌گوییم. اما فضاهای برداری زیاد دیگری مانند فضای تکانه نیز وجود دارند. مکانیک کوانتوم از فضاهای برداری برای توصیف کمیت‌هایی استفاده می‌کند که بردار نیستند. برای درک بهتر این موضوع به مثال دو توپِ نرم و زبر بازمی‌گردیم. یک جهت را به عنوان جهت نرم (Smooth) و جهت دیگر را به عنوان جهتِ زبر (Rough) انتخاب می‌کنیم.

وضعیت توپ کوانتومی، ترکیبی از حالت‌های زبر و نرم است و آن را به عنوان برداری در فضای برداری نشان داده شده در تصویر بالا در نظر می‌گیریم. اگر این توپ در حالت نرم باشد بردار آن به صورت نشان داده شده در تصویر زیر است.

همچنین، اگر این توپ در حالت زبر باشد بردار آن به صورت نشان داده شده در تصویر خواهد بود.

دو بردار نشان داده شده در دو تصویر فوق، بردارهای واحد در فضای بافت توپ هستند. فیزیک کوانتوم گزینه‌های بیشتری برای مشخصه‌ای فیزیکی فراهم می‌کند. این شاخه از فیزیک با هر ذره کوانتومی همانند برداری در فضای برداری رفتار می‌کند. طول بردار حالت، همواره برابر یک است، اما زاویه آن با محورهای فضای برداری می‌تواند تغییر کند. این بدان معنا است که حالت‌های زیادی برای این بردار وجود دارند. فرقی نمی‌کند به چه حالتی نگاه می‌کنیم، نکته مهم آن است که تنها با یک بردار، یک حالت، روبرو هستیم. این واقعیت که هر یک از بردارهای حالت را می‌توانیم به صورت جمع بردارهای دیگر بنویسیم نیز چیزی را تغییر نمی‌دهد. فرض کنید یکی از بردارهای حالت توپ کوانتومی به صورت زیر نوشته می‌شود:

$$ 0.819 | smooth > + 0. 574 | rough> $$

به نوع نوشتاری فوق، ساختار نوشتاری براکت گفته می‌شود. در فضای برداری کوانتومی هر حالت را داخل براکت ($$ | >$$) می‌نویسیم. در ادامه، می‌خواهیم اندازه‌گیری روی حالت بافت (ترکیب زبر و نرم) انجام دهیم. این اندازه‌گیری را می‌توانید با لمس توپ‌ها انجام دهید، اما اندازه‌گیری به این صورت با پیش‌داوری همراه است. همچنین، مثال‌ توپ‌ها، مثالی برای درک بهتر ذرات کوانتومی است و ما نمی‌توانیم ذرات کوانتومی را با دست لمس کنیم. بنابراین، به جای اندازه‌گیری با دست، آشکارسازی بری تشخیص بافت توپ می‌سازیم. این آشکارساز دو حفره به نام‌های نرم و زبر دارد. اگر توپ، نرم باشد، از حفره نرم و اگر زبر باشد از حفره زبر خارج می‌شود.

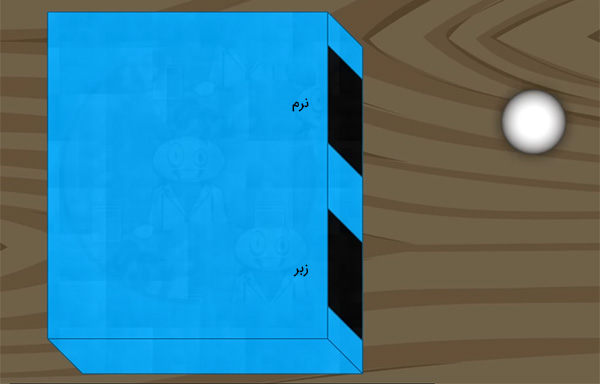
اگر یکی از توپ‌هایی که ترکیب یا برهم‌نهی حالت‌های نرم و زبر است وارد آشکارساز شود، چه اتفاقی رخ می‌دهد؟ آشکارساز چگونه عمل می‌کند؟ نکته مهم در مورد این آشکارساز آن است که توپ‌ها را با دو گروه مجزا مرتب می‌کند و هیچ‌گاه در انجام این کار شکست نمی‌خورد. توپ ترکیبی وارد آشکارساز می‌شود. این توپ نمی‌تواند به دو قسمت تقسیم و هر قسمت جداگانه از حفره‌ها خارج شود. توپ‌ها همانند ذرات کوانتومی، جداناپذیر هستند. بنابراین، به هنگام وارد شدن توپ با بافت ترکیبی به داخل آشکارساز، انتظار یکی از دو اتفاق زیر را داریم:

1. توپ از حفره نرم خارج می‌شود.
2. توپ از حفره زبر خارج می‌شود.

توپ ترکیبی وارد آشکارساز می‌شود و یکی از دو حفره را باید انتخاب کند. این توپ به هنگام پردازش دیگر به صورت برهم‌نهی حالت‌ها نیست. انجام اندازه‌گیری روی توپ، حالت آن را تغییر می‌دهد. این موضوع به خاطر طراحی آشکارساز نیست. هر آشکارسازی با این دو ویژگی، هیچ انتخابی جز اثر گذاشتن بر حالتِ هر چیزی که اندازه‌ می‌گیرد، ندارد:

• ذرات کوانتومی را براساس حالت پایه مرتب می‌کند.
• هرگز شکست نمی‌خورد.

نه آشکارساز و نه توپ‌ها هیچ تصمیم آگاهانه‌ای نمی‌گیرند. انتخاب توسط قوانین فیزیکی انجام می‌شود. این قوانین بر پایه احتمال استوار هستند. بردار حالت به ما می‌گوید این احتمال‌های چه مقدار هستند. اگر توپی نرم باشد، پس از ورود به آشکارساز با احتمال ۱۰۰ درصد از حفره نرم خارج می‌شود. حال اگر توپ ورودی به آشکارساز در حالت $$ 0.819 | smooth > + 0. 574 | rough> $$ قرار داشته باشد، چه اتفاقی رخ می‌دهد؟ این توپ با احتمال $$ || 0.819 || ^ 2 = 0.671$$ یا ۶۷/۱ درصد از حفره نرم و با احتمال $$ || 0.574 || ^ 2 = 0.329$$ یا ۳۲/۹ درصد از حفره زبر خارج می‌شود. در نتیجه، توپ خیالی ما به جای نرم یا زبر بودن، می‌تواند در فضای برداری ساخته شده با بردارهای پایه نرم و زبر، در هر حالتی از ترکیب این دو بردار واحد و پایه قرار داشته باشد.

همچنین، هر حالت ساخته شده از این بردار به عنوان یک حالت کوانتومی در نظر گرفته می‌شوند. ضریب هر بردار پایه به ما احتمال رفتن به هر حالت پایه را می‌دهد. توجه به این نکته مهم است که تعداد حالت‌های پایه می‌تواند بی‌نهایت باشد.

در هم تنیدگی کوانتومی در محاسبات کوانتومی چیست ؟

در بخش‌های قبل به پرسش محاسبات کوانتومی چیست پاسخ دادیم و فهمیدیم کیوبیت و برهم‌نهی کوانتومی چیست. در این بخش، با درهم‌تنیدگی کوانتومی آشنا می‌شویم. درهم‌تنیدگی کوانتومی، نقش مهمی را در محاسبات کوانتومی ایفا می‌کند. فرض کنید برای رفتن از شهری به شهر دیگر، ساعت‌ها است که مشغول رانندگی هستید. ناگهان احساس گرسنگی شدیدی به شما دست می‌دهد. از این‌رو، تصمیم می‌گیرید با مشاهده اولین رستوران متوقف شوید و دو ساندویچ کالباس و همبرگر بخرید. ساندویچ‌ها داخل جعبه‌های یکسانی بسته‌بندی شده‌اند و از طریق پنجره کوچکی به مشتری‌ها داده می‌شوند. دو جعبه یکسان جلوی شما گذاشته می‌شود.

هیچ ایده‌ای ندارید که ساندویچ‌های کالباس و همبرگر داخل کدام جعبه قرار دارند. این مسئله واضح است که اگر جعبه‌ای را باز کنید و ساندویچ کالباس داخل آن باشد، بلافاصله نتیجه می‌گیرید که همبرگر در جعبه دیگر قرار گرفته است. این بدان معنا است که ساندویچ‌های همبرگر و کالباس به گونه‌ای در هم تنیده شده‌اند.

درهم‌تنیدگی کوانتومی مفهومی مشابه مثال ساندویچ‌ها دارد. شرودینگر برای نخستین بار از این اصطلاح استفاده کرد. درهم‌تنیدگی به این معنا است که حالت کوانتومی یک ذره به جزییات حالت کوانتمی ذره دیگر بستگی دارد. به اطراف خود نگاه کنید، هر چیزی که مشاهده می‌کنید با جهان واقعی ارتباط دارد و از قوانین مکانیک کلاسیک پیروی می‌کند. مکانیک کلاسیک شامل قوانین حرکت اجسام است که نخستین بار توسط نیوتن مطرح شد. اگر جسمی بسیار کوچک باشد چه اتفاقی برای آن رخ می‌دهد؟ آیا از قوانین مکانیک کلاسیک پیروی می‌کند؟ خیر. در مقیاس‌های بسیار کوچک، فیزیک کلاسیک جای خود را به فیزیک کوانتوم می‌دهد. ذرات کوانتومی از خود رفتارهای عجیبی نشان می‌دهند. فیزیک کوانتوم، ذرات کوانتومی مانند فوتون‌ها، الکترون‌ها و پروتون‌ها را بررسی می‌کند.

اگر شخصی از شما بپرسد «تو که هستی»، چه پاسخی به او می‌دهید؟ به احتمال بسیار زیاد نام خود را به او می‌گویید. اکنون فرض کنید به سیاره دیگری رفته‌اید و همین سوال از شما پرسیده می‌شود. پس از نام خود خواهید گفت انسان هستید و از زمین آمده‌اید. در این حالت، برای معرفی خود از سه کلمه کلیدی اسم، انسان و زمین، استفاده کرده‌اید. به طور مشابه، در فضای سه‌بعدی از مختصات $$x$$ و $$y$$ و $$z$$ برای تعیین دقیق موقعیت مکانی اجسام مختلف استفاده می‌کنیم. دو جسم می‌توانند مختصات $$x$$ و $$y$$ و $$z$$ یکسانی داشته باشند. اگر فضای چهاربعدی، فضا و زمان، را در نظر بگیریم. در این حالت، دو ذره می‌توانند چهار مختصات یکسان داشته باشند.

به طور مشابه، هر الکترون را می‌توانیم با چهار مختصات یا چهار عدد کوانتومی بشناسیم:

1. عدد کوانتومی اصلی (‌n)
2. عدد کوانتومی فرعی چرخشی (l) یا عدد کوانتومی فرعی
3. عدد کوانتومی مغناطیسی ($$m_l$$)
4. عدد کوانتومی اسپین الکترون ($$m_s $$)

عدد کوانتومی اصلی، n، توصیف کننده انرژی الکترون و محتمل‌ترین فاصله الکترون از هسته است. به بیان دیگر، این عدد اندازه اوربیتال و تراز انرژی را نشان می‌دهد که الکترون در آن قرار دارد. عدد زیرلایه‌ها یا ‌$$l$$ شکل اوربیتال‌ها را تعیین می‌کند. عدد کوانتومی مغناطیسی یا $$m_l$$ تعیین کننده ترازهای انرژی در زیر لایه است. $$m_s $$ نیز مربوط به اسپین الکترون است که در دو حالت بالا یا پایین قرار دارد. در این بخش در مورد عدد کوانتومی اسپین صحبت می‌کنیم. اسپین الکترون دارای دو حالت اسپین بالا و اسپین پایین است. در واقع دارا بودن دو حالت برای اسپین الکترون بدان معنا است که الکترون به صورت پادساعتگرد (اسپین بالا) یا ساعتگرد (اسپین پایین) به دور خود می‌چرخد.

هنگامی‌که می‌گوییم الکترون، اسپین مثبت (بالا)‌ یا منفی (پایین) دارد، این بدان معنا نیست که الکترون واقعا می‌چرخد، بلکه الکترون ممکن است در حالت برهم‌نهی وجود داشته باشد. در بخش قبل در مورد مفهوم برهم‌نهی صحبت کردیم. گربه شرودینگر مثال معروفی از برهم‌نهی است. او در آزمایشی فکری، گربه‌ای را به همراه ماده‌ای رادیواکتیو، سم و آشکارساز، داخل جعبه‌ای مهرو‌موم شده قرار داد. اگر ماده رادیواکتیو تشعشع کند، آشکارساز فعال می‌شود و سم داخل ظرف را آزاد می‌کند. بنابراین، گربه با استشمام ماده سمی کشته می‌شود. اما تشعشع ماده رادیواکتیو، فرایندی تصادفی است. بنابراین،‌ راهی برای پیش‌بینی زمان تشعشع وجود ندارد. قبل از باز کردن جعبه می‌توانیم بگوییم که گربه همزمان در حالت برهم‌نهی زنده یا مرده قرار دارد.

به طور مشابه، هنگامی‌که سکه‌ای روی سطح مسطحی می‌چرخد، در حالتِ برهم‌نهی بین پشت و رو قرار دارد. همچنین، الکترون‌ها در حالت طبیعی در حالتِ برهم‌نهی اسپین‌های بالا و پایین وجود خواهند داشت. پس از اندازه‌گیری اسپین الکترون، به نتیجه اسپین بالا یا اسپین پایین می‌رسیم. به بیان دقیق‌تر و علمی، با اندازه‌گیری اسپین الکترون، تابع موج آن فروپاشیده می‌شود و از بین می‌رود. در فیزیک کوانتوم، به طور معمول تابع موج ابتدا برهم‌نهی تعدادی حالت کوانتومی است که پس از اندازه‌گیری به یکی از این حالت‌ها فروپاشیده می‌شود. به بیان ساده‌تر، هرگونه برهم‌کنشی با محیط خارج سبب فروپاشی تابع موج خواهد شد. هنگامی‌که دو الکترون با یکدیگر برهم‌کنش دارند، حالت‌های اسپین آن‌ها می‌توانند درهم‌تنیده شوند. به این حالت، درهم‌تنیدگی الکترون‌ها گفته می‌شود.

سیستمی متشکل از دو الکترون را در نظر بگیرید. فاصله الکترون‌ها مسئله مهمی برای ما نیست. دو الکترون می‌توانند در فاصله بسیار نزدیکی از یکدیگر باشند یا یکی از آن‌ها روی زمین و دیگری در فاصله چند میلیون سال نوری از آن باشد. همچنین، رفتار الکترون‌ها، مانند مکان و چگونگی حرکت آن‌ها، برای ما مهم نیست، بلکه اسپین برای ما مهم است. الکترون‌ها، دو اسپین دارند:

• اسپین بالا که با $$|\uparrow >$$ نشان داده می‌شود.
• اسپین پایین که با $$|\downarrow >$$ نشان داده می‌شود.

الکترون‌های سیستم دو الکترونی را A و B می‌نامیم.

با اندازه‌گیری اسپین هر یک از این الکترون‌ها به چهار حالت ممکن می‌رسیم:

1. اسپین الکترون‌های A و B در حالت اسپین بالا هستند.
2. اسپین الکترون A در حالت بالا و اسپین الکترون ‌B در حالت پایین قرار دارد.
3. اسپین الکترون A در حالت پایین و اسپین الکترون ‌B در حالت بالا قرار دارد.
4. اسپین هر دو الکترون در حالت پایین است.

آیا پس از اندازه‌گیری اسپینِ الکترون‌ها، به یکی از چهار حالت گفته شده می‌رسیم؟ اگر هیچ سیستم خارجی با سیستم ما برهم‌کنش نداشته باشد، سیستم ما برهم‌نهی تمام چهار حالت ممکن است. به بیان دیگر، سیستم ما شبیه سوپی کوانتومی است که در آن تمام حالت‌های ممکن وجود دارند. بنابراین، هنگامی‌که هیچ اندازه‌گیری روی سیستم انجام نمی‌گیرد و سیستم با هیچ سیستم خارجی دیگری برهم‌کنش ندارد، حالت کلی آن را می‌توان به صورت برهم‌نهی چهار حالت گفته شده و به صورت زیر نوشت:

$$|\psi _ {intial} > = a |\uparrow _ A> | \uparrow _ B> + b |\uparrow _ A> |\downarrow _ B> + c | \downarrow _ A > | \uparrow _ B> + d | \downarrow _ A > |\downarrow _ B>$$

همان‌طور که در رابطه بالا دیده می‌شود، حالت اولیه سیستم، برابر مجموع چهار حالت گفته شده در بالا است. همچنین، هر یک ضریب‌های a و b و c و d، احتمال یافتن سیستم را در یکی از حالت‌ها، به ما می‌دهد. به عنوان مثال، احتمال این‌که اسپین دو الکترون در حالت بالا باشد، برابر مربع ‌a است. تا اینجا فرض کردیم، سیستم کاملا ایزوله است، با هیچ سیستم خارجی برهم‌کنش ندارد و هیچ‌ اندازه‌گیری روی آن انجام نشده است. اگر اسپین الکترون‌ها را اندازه بگیریم، حالت اولیه سیستم فروپاشیده می‌شود و به یکی از چهار حالت تبدیل می‌شود.

اگر سیستم‌های مشابه بسیاری، مشابه سیستم اولیه داشته باشیم، و اسپین الکترون‌های هر یک از آن‌ها را اندازه بگیریم، احتمال یافتن این سیستم‌ها در حالتی خاص، به طور مستقیم با ضریب‌های a و b و c و d، متناسب است. به بیان دیگر، پس از اندازه‌گیری اسپین الکترون‌های A و B برای تمام سیستم‌های مشابه سیستم اولیه، سیستم یک ممکن است در حالت $$ |\uparrow _ A> | \uparrow _ B>$$، سیستم دوم در حالت $$| \downarrow _ A > |\uparrow _ B> $$ و ... باشند. بنابراین، در میان n سیستم یکسان، $$a ^ 2 \times n$$ سیستم در حالت $$ |\uparrow _ A> | \uparrow _ B>$$ خواهد بود. رابطه مشابهی نیز برای حالت‌های دیگر وجود دارد.

بار دیگر به سیستم فرضی خود برمی‌گردیم. این سیستم از دو الکترون به نام‌های A و B تشکیل شده است. در مطالب بالا گفتیم، هنگامی که هیچ اندازه‌گیری روی سیستم انجام نشده باشد، حالت اولیه سیستم، برهم‌نهی کوانتومی تمام حالت‌های ممکن است. به حالت اولیه سیستم دقت کنید، هر قسمت به گونه‌ای نوشته شده است که الکترون‌های A و B به یکدیگر مرتبط باشند. اگر حالت اولیه سیستم را بتوانیم به گونه‌ای بنویسیم که یک قسمت تنها در مورد الکترون A و قسمت دیگر تنها در مورد الکترون B صحبت کند، حالت‌ها جداشدنی هستند و سیستم درهم تنیده نخواهد بود.

$$(\alpha | \uparrow _ A > + \beta | \downarrow _ A > ) \times (\gamma | \uparrow _ B > + \delta | \downarrow _ B > )$$

الکترون‌های در هم‌تنیده، تنها می‌توانند اسپین‌های مخالف یکدیگر داشته باشند. این بدان معنا است که اگر اسپین یکی از الکترون‌ها پس از اندازه‌گیری در حالت بالا قرار داشته باشد، اسپین الکترون دوم بلافاصله در حالت پایین قرار می‌گیرد. دو الکترون قبل از اندازه‌گیری در حالت برهم‌نهی اسپین‌های بالا و پایین قرار دارند. اکنون دو الکترون را از یکدیگر جدا می‌کنیم و یکی از آن‌ها را روی زمین و دیگری را در کهکشان آندرومدا قرار می‌دهیم. سپس، اسپین الکترون روی زمین را اندازه‌ می‌گیریم و می‌فهمیم اسپین آن به سمت بالا است. با انجام این اندازه‌گیری و فهمیدن جهت اسپین الکترون روی زمین، بلافاصله می‌فهمیم که اسپین الکترون در کهکشان آندرومدا رو به پایین قرار دارد. این اطلاعات به صورت آنی منتقل شده است، سریع‌تر از سرعت نور. بنابراین، درهم‌تنیدگی کوانتومی موضوعی آزادهنده برای اینشتین بود.

ناهمدوسی کوانتومی چیست؟

به از بین رفتن همدوسی کوانتومی، ناهمدوسی کوانتومی در فیزیک و محاسبات کوانتومی گفته می‌شود. بر طبق همدوسی کوانتومی، ذره یا جسمی تک، تابع موجی دارد که می‌تواند به دو موج جداگانه تقسیم شود. هنگامی‌که این دو موج به صورت همدوس با یکدیگر عمل کنند، همدوسی کوانتومی رخ می‌دهد. در این بخش می‌خواهیم بدانیم نقش ناهمدوسی در محاسبات کوانتومی چیست.

فیلم آموزش نرم افزار متمتیکا – حل محاسبات کوانتومی با Mathematica در فرادرس

کلیک کنید

وظیفه ناهمدوسی کوانتومی آن است که سیستمی کوانتومی را به صورت ظاهری به حالت کلاسیک ببرد. سیستم کوانتومی و کلاسیک چه تفاوت یا تفاوت‌هایی با یکدیگر دارند؟ تفاوت اصلی آن‌ها در مفهومی به نام برهم‌نهی حالت‌ها نهفته است که در بخش‌های قبل در مورد آن صحبت کردیم. در فیزیک کلاسیک به راحتی می‌گوییم که ذره‌ای در مکان $$( x, y , z )$$ قرار دارد. در فیزیک کوانتوم به جای بیان مکان دقیق ذره، می‌گوییم ذره در حالت برهم‌نهی موقعیت‌های $$( x_ 1 , y _ 1, z _ 1 )$$ و $$( x_ 2 , y _ 2 , z _  2 )$$ قرار گرفته است. به هنگام اندازه‌گیری موقعیت مکانی ذره، آن را در یکی از دو موقعیت گفته شده پیدا خواهیم کرد.

به بیان دیگر، تابع موج ذره قبل از اندازه‌گیری به صورت برهم‌نهی این دو موقعیت نوشته می‌شود، اما پس از اندازه‌گیری به یکی از آن‌ها فروپاشیده می‌شود. تفسیر و درک این موضوع برای ذهن کلاسیکی ما کمی دشوار است. به این موضوع مشکل اندازه‌گیری گفته می‌شود. به هنگام اندازه‌گیری، تابع موج فروپاشیده می‌شود. این موضوع قابل‌درک است. اما اگر اندازه‌گیری انجام نشود، چه اتفاقی رخ می‌دهد؟ دینامیک یا پویایی و فرض فروپاشی به هنگام اندازه‌گیری به طور کامل با یکدیگر در تضاد هستند. این‌گونه به نظر می‌رسد که فرضیه فروپاشی در مورد آنچه به هنگام اندازه‌گیری رخ می‌دهد، صحیح و دینامیک به صورت عجیبی در مورد آنچه به هنگام اندازه‌گیری اتفاق می‌افتد، نادرست و غلط است.

اما دینامیک هنگامی که اندازه‌گیری انجام نمی‌شود، صحیح به نظر می‌رسد. «ون نیومن»‌ (Von Neumann) نخستین کسی بود که «دوگانگی دینامیکی»‌ (Dynamical Dualism) را مطرح کرد. این دوگانگی بر فرمول‌بندی مکانیک کوانتوم تاثیر گذاشت. همچنین، بور به هنگام مطرح کردن «جهش کوانتومی» (Quantum Leap) به این دوگانگی اشاره کرده بود. تکامل و تحولات سیستمی کوانتومی با استفاده از معادله شرودینگر توصیف می‌شود. این معادله را به سیستمی ایزوله و به دور از جهان اطراف، اعمال می‌کنیم.

$$i \hbar \frac{\partial }{\partial t} | \psi > = H | \psi > $$

علاوه بر تحول معمول در سیستم کوانتومی که توسط معادله شرودینگر توصیف می‌شود، تحول دیگری نیز وجود دارد که به هنگام اندازه‌گیری رخ می‌دهد، فروپاشی به هنگام اندازه‌گیری.

$$| \psi > = \sum_n c_n | n >\ \rightarrow \ | n _ i > $$

از نظر فنی، نیومن معادله $$| \psi > = \sum_n c_n | n >\ \rightarrow \ | n _ i > $$ را مداخل اول و معادله $$i \hbar \frac{\partial }{\partial t} | \psi > = H | \psi > $$ را مداخله دوم نامید. مداخله اول همان چیزی است که از آن به عنوان فروپاشی موج یاد می‌شود. در فروپاشی موج، برهم‌نهی حالت‌ها پس از اندازه‌گیری، به یک حالت کوانتومی فروپاشیده می‌شود. ناهمدوسی کوانتومی چارچوبی نظری ارائه می‌دهد که در آن مشکل اندازه‌گیری می‌تواند به زیر فرش جارو یا به سیستمی بزرگ‌تر منتقل شود. همان‌طور که در ابتدای این بخش اشاره کردیم، ناهمدوسی هنگامی رخ می‌دهد که ذره کوانتومی همدوسی خود را از دست می‌دهد. اما سوالی که ممکن است مطرح شود آن است که همدوسی چیست؟

ذره کوانتومی در حالت همدوس همانند موج رفتار می‌کند و ویژگی‌های عجیب کوانتومی از خود نشان می‌دهد. در مقابل، در حالت ناهمدوس، همین ذره به شکل ذره آشکار می‌شود که از قوانین فیزیک و الکترومغناطیس کلاسیک پیروی می‌کند. ذره در حالت ناهمدوس هیچ‌گونه رفتار عجیب کوانتومی از خود نشان نمی‌دهد. ناهمدوسی همان معنای فیزیکی فروپاشی تابع موج است. ناهمدوسی کوانتومی، ویژگی ذره کوانتومی است. ذره کوانتومی همدوس در حالت کوانتومی خود قرار دارد. در این حالت، ذره، برهم‌نهی بسیاری از حالت‌های دیگر است. به بیان دیگر، در حالت همدوس، ذره کوانتومی همانند مجموعه‌ای عجیب از امواج عمل می‌کند. به عنوان مثال، فوتون در حالت همدوس همزمان می‌تواند در موقعیت‌های A و B و C قرار داشته باشد.

فرض کنید مکان C، وسط شبکیه قورباغه‌‌ای قرار دارد. لحظه‌ای خاص در شب، فوتون به مکان C می‌رود و پس از برخورد با شبکیه قورباغه، توسط الکترونی داخل شبکیه جذب می‌شود. بنابراین، فوتون حالت برهم‌نهی خود را از دست می‌دهد و برای لحظه‌ای کوتاه، مکان C را اشغال می‌کند. فوتون در این لحظه، حالت ناهمدوسی دارد و همانند ذره‌ای معمولی رفتار می‌کند. معادله شرودینگر، توصیفی ریاضی از رفتار همدوسی کوانتومی ذرات ارائه و احتمال قرار گرفتن ذره در مکان‌های مختلف را به ما می‌دهد. در مثال فوتون و شبکیه چشم قورباغه، از معادله شرودینگر برای محاسبه احتمال حضور فوتون در مکان A، مکان B یا مکان C استفاده می‌شود. هنگامی‌که فوتون ناهمدوس و در مکان C یافت شود، تابع موج آن به حالت C فروپاشیده شده است.

کامپیوترهای کوانتومی بر ذره کوانتومی، الکترون یا اتم، تکیه دارند. این ذره به صورت برهم‌نهی تعداد زیادی حالت کوانتومی است. ذره کوانتومی پس از برهم‌کنش با ذرات دیگر، حالت برهم‌نهی خود را از دست می‌دهد و ناهمدوس می‌شود. نکته اصلی به هنگام انجام محاسبات کوانتومی و کار با کامپیوترهای کوانتومی آن است که ذره کوانتومی را ایزوله نگه داریم تا بتواند حالت برهم‌نهی خود را تا جایی که ممکن است حفظ کند. این کار را می‌توانیم با نگه داشتن الکترون یا اتم در خلأ و پایین آوردن دما تا حد امکان انجام داد. در برخی آزمایشات انجام شده به هنگام محاسبات کوانتومی، اتم در محفظه‌ای با خلأ بسیار بالا نگه داشته می‌شود. در این حالت، اتم می‌تواند حالت برهم‌نهی خود را تا ۱۰ دقیقه حفظ کند.

اتم توسط میدان مغناطیسی، داخل محفظه خلأ باقی می‌ماند و هیچ‌ برهم‌کنشی با دیواره‌های محفظه و محیط بیرون ندارد. هوای داخل محفظه توسط پمپ خارج و فشار آن تا ۱۰۰ تریلیون مرتبه کوچک‌تر از فشار هوا شده است.

الگوریتم های کوانتومی در محاسبات کوانتومی چیست ؟

در پاسخ به پرسش محاسبات کوانتومی چیست فهمیدیم به قسمتی از علوم کامپیوتر که در آن از مفاهیم فیزیک کوانتوم استفاده می‌شود، محاسبات کوانتومی گفته می‌شود. برای کار در این حوزه باید با مفاهیم بنیادی در فیزیک کوانتوم مانند برهم‌نهی، درهم‌تنیدگی، ناهمدوسی و کیوبیت آشنا باشیم. پس از آشنایی با این مفاهیم، نوبت به فهمیدن الگوریتم‌های کوانتومی می‌رسد. الگوریتم کوانتومی، الگوریتمی است که بر روی مدلی واقعی از محاسبات کوانتومی اجرا می‌شود. مدل مدار کوانتومی یکی از رایج‌ترین مدل‌های استفاده شده است. الگوریتم کلاسیکی یا غیرکوانتومی از تعدادی راهکارهای متوالی ساخته شده است که با استفاده از آن می‌توانیم مسئله‌ای را قدم به قدم حل کنیم. هر مرحله از الگوریتم کلاسیک می‌تواند روی کامپیوتر کلاسیک اجرا شود.

فیلم آموزش محاسبات کوانتومی در فرادرس

کلیک کنید

به طور مشابه، الگوریتم کوانتومی نیز فرایندی مرحله به مرحله است که هر یک از مرحله‌ها می‌تواند روی کامپیوتر کوانتومی اجرا شود. برخی از مسائل را شاید بتوان با استفاده از الگوریتم‌های کوانتومی، سریع‌تر از الگوریتم‌های کلاسیک حل کرد. دلیل این موضوع آن است که برهم‌نهی و درهم‌تنیدگی کوانتومی در کامپیوترهای معمولی به خوبی نمی‌توانند شبیه‌سازی شوند. دو الگوریتم «شور» (Shor's Algorithm) و «گرووِر» (Grover's Algorithm) از معروف‌ترین الگوریتم‌های کوانتومی هستند که از آن‌ها برای جستجو در لیست نامنظم استفاده می‌شود. در ادامه، الگوریتم شور را توضیح می‌دهیم.

الگوریتم شور در محاسبات کوانتومی چیست؟

الگوریتم شور، الگوریتمی کوانتومی است که از آن برای یافتن عوامل اولِ عددی صحیح استفاده می‌شود. این الگوریتم در سال ۱۹۹۴ میلادی توسط ریاضی‌دانی آمریکایی به نام «پیتر شور» (Peter Shor) بسط داده شد. به‌دست آوردن عوامل اول اعداد بزرگ همواره چالشی برای ریاضی‌دان‌ها بوده است. ضرب دو عدد و محاسبه حاصل‌ضرب آن‌ها کاری آسان، اما نوشتن نتیجه حاصل‌ضرب برحسب عوامل اول آن، کاری خسته‌کننده و طاقت‌فرسا است. نوشتن عوامل اولِ اعداد صحیح بسیار بزرگ حتی با وجود کامپیوترهای قدرتمند و بسیار سریع هنوز هم به عنوان یکی از مسائل سخت در نظر گرفته می‌شود. سرانجام، شور در سال ۱۹۹۴ میلادی الگوریتمی را برای به‌دست آوردن عوامل اول اعداد صحیح برای کامپیوترهای کوانتومی نوشت.

الگوریتم شور یکی از بهترین الگوریتم‌ها برای به‌دست آوردن عوامل اول اعداد صحیح است. برای آشنایی با این الگوریتم ابتدا در مورد چند مفهوم پایه در ریاضیات با یکدیگر صحبت می‌کنیم.

بزرگ‌ترین مقسوم‌ علیه مشترک

مفهوم بزرگ‌ترین مقسوم‌علیه مشترک یا ب.م.م را با مثالی ساده توضیح می‌دهیم. دو عدد ۷۵ و ۱۵ را در نظر بگیرید. برای به‌دست آوردن ب.م.م این دو عدد، ابتدا مقسوم‌علیه‌های مشترک هر یک از آن‌ها را به صورت جداگانه می‌نویسیم:

• مقسوم علیه‌های ۷۵: ۱، ۳، ۵، ۱۵، ۲۵ و ۷۵
• مقسوم‌علیه‌های ۱۵: ۱، ۳، ۵ و ۱۵

همان‌طور که مشاهده می‌کنید مقسوم‌علیه‌های مشترک ۱۵ و ۷۵ برابر اعداد ۱، ۳، ۵ و ۱۵ هستند. بنابراین، ب.م.مِ این دو عدد برابر ۱۵ است. ب.م.م دو عدد a و b به صورت $$GSC ( a , b) $$ نوشته می‌شود. به عنوان مثال، ب.م.م دو عدد ۱۵ و ۷۵ را به صورت زیر می‌نویسیم:

$$GDC ( 15 , 75 ) = 15 $$

روش‌های مختلفی برای به‌دست آوردن بزرگ‌ترین مقسوم‌علیه مشترک وجود دارند که «الگوریتم تقسیم اقلیدسی» (Euclid's Division Algorithm)‌ یکی از بهترین روش‌ها است.

عملیات پیمانه ای

در عملیات پیمانه‌ای باقی‌مانده تقسیم عددی بر عدد دیگر را به‌دست می‌آوریم. پیمانه با mod نشان داده می‌شود. به عنوان مثال، $$ 17 \enspace mod \enspace 5 $$ برابر ۲ است.

قبل از توضیح در مورد الگوریتم شور به این نکته توجه داشته باشید که تمام اعداد را نمی‌توانیم با استفاده از الگوریتم شور برحسب عوامل اول بنویسیم. به هنگام استفاده از این الگوریتم باید به سه نکته توجه داشته باشیم:

1. عدد انتخاب شده نباید عدد اول باشد.
2. عدد زوج نباید باشد، زیرا ۲ یکی از عوامل اول است.
3. به شکل $$ n ^ x $$ نباشد.

پس از انتخاب عددی که سه شرط بالا را داشته باشد، گام‌های زیر را به ترتیب طی می‌کنیم.

گام اول

عددی که می‌خواهیم عوامل اول آن را به‌دست آوریم N می‌نامیم. فرض کنید N برابر ۱۵ است.

گام دوم

عددی تصادفی بین ۱ تا N انتخاب کنید و آن را k بنامید. اگر N برابر ۱۵ باشد، k عددی تصادفی بین یک تا ۱۵ خواهد بود. فرض کنید مقدار k برابر ۷ است.

گام سوم

ب.م.م دو عدد N و k را به‌دست آورید. برای انجام این کار می‌توانید از الگوریتم اقلیدسی استفاده کنید. اگر ب.م.م N و k برابر یک نبود، کار تمام است. اما اگر ب.م.م برابر یک بود، وارد چهارمین گام می‌شویم. از آنجا که ب.م.م ۱۵ و ۷ برابر یک است، کار را با چهارمین گام ادامه می‌دهیم.

گام چهارم

در این مرحله، کوچک‌ترین عدد طبیعی مثبت r را به گونه‌ای پیدا می‌کنیم که:

$$f ( x ) k ^ x , \ then \ f ( z ) = f ( a+ r) $$

عبارت بالا شاید کمی شما را بترساند. اما برای یافتن r تنها کافی‌ است سه بخش زیر را به ترتیب طی کنید.

بخش یکم

متغیری جدید به نام q تعریف کنید. در اینجا q را برابر یک انتخاب می‌کنیم.

بخش دوم

مقدار $$( q \times k ) mod ٔ $$ را به‌دست آورید. اگر باقی‌مانده برابر یک به‌دست آمد، به گام سوم بروید. اگر مقدار باقی‌مانده یک نشد، مقدار q را برابر مقدار باقی‌مانده‌ای قرار دهید که به‌دست می‌آوریم. بخش ۲ را تا زمانی اجرا کنید که که مقدار باقی‌مانده برابر یک شود. همچنین، تعداد مرحله‌های طی شده تا رسیدن به باقی‌مانده یک را به خاطر بسپارید. همچنین، فراموش نکنید که مقدار q را در هر مرحله تغییر دهید. بخش دوم برای اعداد انتخاب شده به صورت زیر انجام می‌شود. همان‌طور که در تصویر زیر مشاهده می‌کنید تعداد مرحله‌های طی شده تا رسیدن به باقی‌مانده یک، برابر ۴ است.

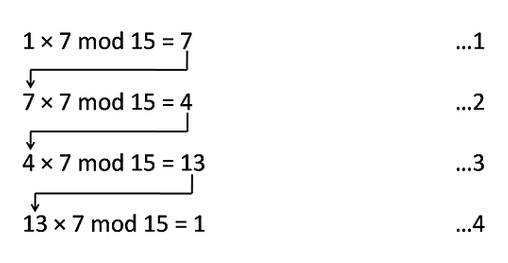
بخش سوم

r برابر تعداد مرحله‌های طی شده تا رسیدن به باقی‌مانده یک در گام دوم، یعنی برابر ۴ است.

گام پنجم

اگر r عددی فرد باشد، به گام دوم برمی‌گردیم. در گام چهارم و در بخش سوم، مقدار r برابر ۴ به‌دست آمد، بنابراین به راه خود ادامه می‌دهیم.

گام ششم

از آنجا که r عددی زوج است آن را بر ۲ تقسیم می‌کنیم. حاصل تقسیم r بر ۲ برابر شماره مرحله‌‌ای است که برای رسیدن به باقی‌مانده یک در گام چهارم و بخش دوم طی شده است. باقی‌مانده این مرحله را p می‌نامیم. اگر p+1 برابر N باشد، به گام دوم برمی‌گردیم و مقدار متفاوتی را برای k انتخاب می‌کنیم. در غیر این صورت، به گام هفتم می‌رویم. از آنجا که در مثال ما مقدار r برابر ۴ به‌دست آمد، با تقسیم آن بر ۲، عدد ۲ به‌دست می‌آید. یعنی باید به بخش دوم از گام چهارم برویم و باقی‌مانده را نگاه کنیم. مقدار باقی‌مانده برابر ۴ است. جمع ۴ و یک برابر ۵ می‌شود که برابر ۱۵ نیست. در نتیجه، با خیال راحت می‌توانیم به راه خود ادامه دهیم.

گام هفتم

گام هفتم، آخرین گام است. عوامل اول N به صورت زیر به‌دست می‌آیند:

$$ f_ 1 = GCD \ ( p+ 1 , N) \\ f_ 2 = GCD \ ( p -1 , N ) $$

به عنوان مثال، عامل‌های اول عدد ۱۵ برابر هستند با:

$$ f_ 1 = GCD \ ( p+ 1 , N) \\ = GCD \ ( 5 , 15) = 5\\ f_ 2 = GCD \ ( p -1 , N ) \\ = GCD \ ( 3 , 15 ) = 3  $$

کوانتوم و رمزگذاری

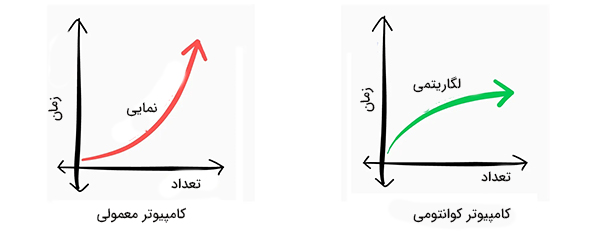
الگوریتم شور برای اجرا در کامپیوتر‌های کوانتومی طراحی شده است. این الگوریتم در کامپیوترهای کوانتومی بسیار سریع‌تر کار می‌کند. چرا؟ به این نکته توجه داشته باشید که گام‌های یک، دو، سه، پنج، شش، و هفت در کامپیوترهای معمولی به خوبی انجام می‌شوند. اما در گام چهار و به هنگام پیدا کردن r، کامپیوتر معمولی کم می‌آورد. گام چهارم از میان هفت گام، زمان بیشتری را به خود اختصاص می‌دهد. اما کامپیوترهای کوانتومی این مرحله را به سرعت و به راحتی انجام می‌دهند. در تصویر زیر، نمودار زمان برحسب تعداد در کامپیوترهای معمولی و کوانتومی با یکدیگر مقایسه شده‌اند. بنابراین، برای به‌دست آوردن عوامل اول اعداد طبیعی بسیار بزرگ، کامپیوتر کوانتومی گزینه مناسب‌تری نسبت به کامپیوتر معمولی است.

محاسبات کوانتومی گرچه پیشرفتی چشم‌گیر در محاسبات و ریاضی به نظر می‌رسد، اما تهدید بزرگی برای رمزنگاری محسوب می‌شود. «الگوریتم RSA» یا (Rivest–Shamir–Adleman | RSَ) الگوریتم رمزنگاری نامتقارن است. از آنجا که این الگوریتم روی دو کلید مختلف عمومی و خصوصی کار می‌کند، الگوریتمی نامتقارن در نظر گرفته می‌شود. کلید عمومی همان‌گونه که از نام آن مشخص است در دسترس همه قرار دارد، اما کلید خصوصی به صورت خصوصی و دور از دسترس عموم قرار گرفته می‌شود. RSA که یکی از پرکاربردترین طرح‌ها در رمزنگاری است، به این فرض وابسته است که یافتن عوامل اولِ اعداد بسیار بزرگ عملا غیرممکن است. اگر به گونه‌ای بتوانیم عوامل اول اعداد بزرگ را به‌دست آوریم، RSA شکسته خواهد شد. بنابراین، با الگوریتم شور و با استفاده از کامپیوتر کوانتومی می‌توان این کار را انجام داد.

کد الگوریتم شور در زبان برنامه‌نویسی پایتون به صورت زیر نوشته می‌شود:

1from qiskit import IBMQ
2from qiskit.aqua import QuantumInstance
3from qiskit.aqua.algorithms import Shor
4
5# Enter your API token here
6IBMQ.enable_account('ENTER API TOKEN HERE') 
7provider = IBMQ.get_provider(hub='ibm-q')
8
9# Specifies the quantum device
10backend = provider.get_backend('ibmq_qasm_simulator')
11
12print('\n Shors Algorithm')
13print('--------------------')
14print('\nExecuting...\n')
15
16# Function to run Shor's algorithm 
17# where 35 is the integer to be factored
18factors = Shor(35)
19
20result_dict = factors.run(QuantumInstance(
21	backend, shots=1, skip_qobj_validation=False))
22
23# Get factors from results
24result = result_dict['factors'] 
25
26print(result)
27print('\nPress any key to close')
28input()

Shors Algorithm
 - - - - - - - - - - - - - 
Executing... 
[[5,7]]
Press any key to close

کاربردهای محاسبات کوانتومی چیست ؟

در بخش‌های قبل فهمیدیم:

• محاسبات کوانتومی چیست.
• مفهوم درهم‌تنیدگی، برهم‌نهی و کیوبیت در محاسبات کوانتومی چیست.
• نقش الگوریتم‌های کوانتومی مانند الگوریتم شور در محاسبات کوانتومی چیست.

در این بخش، می‌خواهیم بدانیم مهم‌ترین کاربردهای محاسبات کوانتومی چیست و چگونه می‌توان از آن در بخش‌های مختلف زندگی استفاده کرد. محاسبات کوانتومی در دهه ۱۹۸۰ میلادی متولد شد. در آن دهه بسیاری از پژوهشگران به این نتیجه رسیدند که برخی مسائل محاسباتی را با استفاده از الگوریتم‌های کوانتومی بسیار بهتر از الگوریتم‌های کلاسیک می‌توان حل کرد. برخی از مهم‌ترین کاربردهای محاسباتی کوانتومی عبارت هستند از:

• مالی: موسسات مالی با استفاده از محاسبات کوانتومی می‌توانند پرتفوی سرمایه‌گذاری موثرتری را برای مشتریان خرده‌فروشی و سازمانی طراحی کنند. همچنین، معاملات مالی را می‌توان به صورت بسیار موثرتری شبیه‌سازی کرد.
• سلامتی: صنعت سلامت با استفاده از محاسبات کوانتومی می‌تواند دارو‌های جدیدی بسازد و درمان‌های ژنتیکی را به صورت موثرتری انجام دهد. همچنین، پژوهش‌های مبتنی بر DNA پیشرفت قابل‌توجهی خواهند کرد.
• امنیت: با کمک محاسبات کوانتومی می‌توان رمزنگاری داده‌ها را با طراحی بسیار بهتری انجام داد.

محدودیت های محاسبات کوانتومی چیست ؟

گرچه محاسبات کوانتومی کاربردهای بسیاری دارد، از محدودیت‌های آن نباید غافل شویم:

• ناهمدوسی کوانتومی می‌تواند با کوچک‌ترین اختلالی در محیط کیوبیت ایجاد شود. از این‌رو، محاسبات به راحتی از بین می‌روند یا اشتباهات فاحشی به هنگام انجام محاسبات رخ می‌دهند. بنابراین، کامپیوتر کوانتومی به هنگام انجام محاسبات باید از تمام اختلال‌های خارجی به دور باشد.
• تصحیح خطا به هنگام محاسبات کامل نشده است، بنابراین نتیجه محاسبات غیرقابل‌اعتماد است. از آنجا که کیوبیت‌ها ذرات کوانتومی هستند که هم‌زمان می‌توانند دو حالت کوانتومی صفر و یک داشته باشند، راه‌حل‌های استفاده شده برای تصحیح خطا در کامپیوترهای معمولی را نمی‌توان برای آن‌ها استفاده کرد.
• بازیابی نتایج محاسباتی می‌تواند منجر به از بین رفتن داده‌ها شود.
• امنیت و رمزنگاری کوانتومی هنوز به طور کامل توسعه نیافته‌اند.
• کمبود کیوبیت‌ها از دستیابی کامپیوترهای کوانتومی به قابلیت‌های کاربردی جلوگیری می‌کند. پژوهشگران هنوز موفق نشده‌اند بیش از ۱۲۸ کیوبیت تولید کنند.

کامپیوترهای کوانتومی برای آن‌که بتوانند به درستی کار کنند باید از فشار هوا و میدان مغناطیسی زمین دور نگه داشته شوند و دمای محیطی که در آن قرار دارند باید در حدود صفر مطلق باشد.

کامپیوتر کوانتومی و کامپیوتر معمولی چه تفاوت هایی با یکدیگر دارند؟

کامپیوترهای کوانتومی ساختار ساده‌تری نسبت به کامپیوترهای معمولی دارند. کامپیوتر کوانتومی حافظه یا پردازنده‌ای ندارد. کامپیوتر کوانتومی از مجموعه‌ای از کیوبیت‌های ابررسانا استفاده می‌کند. پردازش اطلاعات در کامپیوتر معمولی و کوانتومی با یکدیگر تفاوت دارد. توان پردازش کامپیوترهای کوانتومی با اضافه شدن کیوبیت به آن‌ها به صورت نمایی افزایش می‌یابد. در مقابل، توان پردازش کامپیوتر معمولی با افزودن بیت به آن به صورت خطی افزایش خواهد یافت. شرکت گوگل با خرج میلیاردها دلار تصمیم دارد تا سال ۲۰۲۹ میلادی کامپیوتر کوانتومی خود را بسازد.

جمع‌بندی

در این مطلب از مجله فرادرس فهمیدیم محاسبات کوانتومی چیست. محاسبات کوانتومی حوزه‌ای از علوم کامپیوتر است که بر توسعه فناوری‌های مختلف با استفاده از فیزیک کوانتوم تمرکز دارد. محاسبات کوانتومی از رفتارهای منحصربه‌فرد و جالب فیزیک کوانتوم برای حل مسائل بسیار پیچیده‌ای استفاده می‌کند که کامپیوترهای معمولی از عهده حل آن‌ها برنمی‌آیند. با ساخت کامپیوترهای کوانتومی می‌توان به این دستاورد رسید. پس از آشنایی با مفهوم محاسبات کوانتومی، فهمیدیم:

• نقش برهم‌نهی و درهم‌تنیدگی کوانتومی در انجام محاسبات کوانتومی چیست.
• چگونه می‌توان از الگوریتم‌های کوانتومی در انجام محاسبات کوانتومی استفاده کرد.
• محدودیت‌ها و مزایای محاسبات کوانتومی چیست.

محاسبات کوانتومی بی‌شک در آینده‌ای نه چندان دور تحول بزرگی را در زنگی انسان ایجاد می‌کند.