کیوبیت — به زبان ساده

همه ما کم و بیش با تعریف بیت آشناییم و شاید چندین بار در طول روز از کلمه بیت استفاده کنیم. بیت کوچکترین واحد برای پردازش اطلاعات کلاسیکی بوده و فقط میتواند دو مقدار ثابت ۰ یا ۱ را داشته باشد. درواقع بیت عددی در دستگاه اعداد دودویی است. بیتها توسط گیتهایی پردازش میشوند که اکثراً با خیلی از آنها نظیر گیت AND ،OR ،NOT ،XOR و ... آشناییم. یک بیت در هر لحظه فقط یکی از حالت های مشخص ۰ یا ۱ را میتواند داشته باشد. حال فرض کنید به جای بیت، موجودیت جدیدی در دست داشته باشیم که در هر لحظه بتواند هر دو مقدار ۰ و ۱ را به طور همزمان داشته باشد؛ در این صورت چه اتفاقی رخ میداد؟! با ما در ادامه این مقاله همراه باشید تا با واحدی شگفتانگیز به نام کیوبیت آشنا شوید.

بیت کوانتومی یا کیوبیت
بر اساس تعریفی مشابه با بیت کلاسیکی، میتوانیم واحد پردازش اطلاعات کوانتومی را تعریف و واژه بیت کوانتومی یا «کیوبیت» (Qubit) را به آن اطلاق کنیم. از آنجا که در دنیای کوانتوم، حالتهای کوانتومی (نظیر وضعیت اسپین یک الکترون) را با بردارها نمایش میدهند، کیوبیت نیز یک بردار حالت در فضای دوبعدی هیلبرت است. در تشابه با یک بیت کلاسیکی، کیوبیت میتواند دو حالت پایه و را داشته باشد (بخوانید کِت ۰ و کِت ۱).
اما بر خلاف بیت کلاسیک که در هر لحظه فقط یکی از دو مقدار ۰ یا ۱ را میتواند داشته باشد، کیوبیت میتواند در حالت «برهمنهی» (Superposition) از حالتهای پایه و به فرم زیر باشد. در مقاله درهمتنیدگی، دیدیم که وقتی حالت یک سیستم کوانتومی در زیرحالتهایی همبسته توزیع شده باشد، تا قبل از اندازهگیری نمیتوانیم بگوییم که سیستم با چه احتمالی در کدام یک از زیر حالتها قرار دارد.
,
در رابطه فوق مربع قدرمطلق ضرایب (همان اعمال اندازهگیری)، احتمال یافتن کیوبیت در آن حالت را نتیجه میدهد. یعنی داریم:
- احتمال یافتن کیوبیت در حالت برابر است با:
- احتمال یافتن کیوبیت در حالت برابر است با:
توجه داشته باشید که ضرایب α و β در حالت کلی اعدادی مختلط به فرم بوده که در آن است. میدانیم که جمع احتمالات یک سیستم یا پدیده باید ۱ باشد، پس این شرط ایجاب میکند که:
مثالی از برهمنهی
برای اینکه درک سادهتری از مفهوم کیوبیت داشته باشید، مثال زیر را در نظر بگیرید. فرض کنید که یک سکه را درون جعبهای انداخته و تکان میدهیم. به نظر شما وضعیت سکه به چه صورت است؟ احتمالاً پاسخ میدهید که حالت سکه یا شیر و یا خط است. اما از نقطه نظر مکانیک کوانتومی وضعیت سکه نه شیر است و نه خط، بلکه وضعیت آن به صورت برهمنهی از حالت شیر و خط است. در واقع تا قبل از باز کردن در جعبه نمیتوانیم وضعیت سکه را با یک بیت کلاسیکی معادل سازی کنیم، بلکه وضعیت سکه در این حالت یک کیوبیت به فرم زیر است:
وضعیت گربه داخل جعبه شرودینگر (زنده یا مرده!) هم می تواند مثالی از یک کیوبیت باشد. در اینجا نیز قبل از اندازهگیری نمیتوانیم به طور ۱۰۰٪ در مورد وضعیت گربه که آن را با یک کیوبیت معادلسازی کردیم، اظهار نظر کنیم.

کره بلوخ (Bloch Sphere)
برای درک شهودی از وضعیت یک کیوبیت، نمایش آن روی کره بلوخ میتواند مناسب باشد. در واقع یک کیوبیت هر مکانی را روی سطح کره بلوخ میتواند به طور همزمان اختیار کند. این در حالی است که یک بیت کلاسیکی تنها دو مقدار ۰ و ۱ را بر روی قطبهای کره بلوخ دارد.
با تعریف ضرایب α و β به فرم زیر میتوان حالت یک کیوبیت را روی کره بلوخ نمایش داد. یادآور میشویم که قبل از اندازهگیری سیستم، مکان کیوبیت در هر نقطهای روی سطح کره بلوخ میتواند باشد، در واقع با اندازهگیری یعنی تعیین ضرایب میتوان مکان و وضعیت دقیق کیوبیت را مشخص کرد.
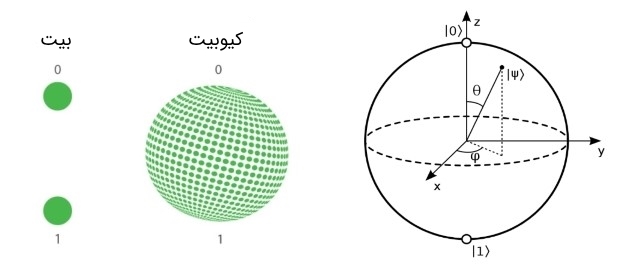
حال به نظر میرسد پاسخ پرسشی که در مقدمه متن عنوان شد را با توجه به توضیحات فوق و کره سبز رنگ شکل فوق بتوان داد. بله، درست حدس زدید، پردازش موازی و سرعت بیشتر!
تحقق فیزیکی
پیادهسازی یک بیت کلاسیک به روشهای مختلفی مثل روشن یا خاموش شدن یک پالس لیزری یا دو سطح مختلف ولتاژ مثل 0 و ۵ ولت صورت میگیرد. برای پیادهسازی یک کیوبیت نیز هر سیستم دو حالته ریز مقیاس فیزیکی، نظیر اسپین Up و Down یک الکترون یا قطبش افقی و عمودی یک فوتون میتواند مصداق یک کیوبیت باشد. به طور مثال برای کیوبیتهای فوتونی، را قطبش افقی و را قطبش عمودی به شکل زیر تعریف میکنیم:
یک سیستم کوانتومی به شدت نسبت به محیط اطراف خود نویز پذیر بوده و کوچکترین اختلالی در سیستم، حالتهای کوانتومی را دچار تغییر میکند، بنابراین سیستم باید به شدت از محیط بیرون ایزوله باشد که معمولا این کار را با اعمال خلأ بسیار بالا یا دماهایی خیلی پایین (نزدیک به صفر کلوین) انجام میدهند. درواقع همین مسئله تا به امروز گلوگاه تکنولوژیکی برای بهره بردن از مزایای کیوبیت و کامپیوترهای کوانتومی در شرایط عادی است.

تاکنون روشهای متعددی برای پیادهسازی کیوبیتها معرفی شده است که هر کدام مزایا و معایب خاص خود را دارند. اما شاید در دسترسترین گزینه پیش رویمان، استفاده از فوتون و سیستمهای اپتیکی است. چرا که فوتونها در حالت عادی با یکدیگر برهمکنشی نداشته و نویزپذیر از محیط اطراف خود (البته در شرایط معمولی) نیستند. همچنین نیازی به خلأ یا سرد کردن ندارند. از طرفی دسترسی و کار با ادوات اپتیکی و لیزرها به عنوان منبعی برای تولید فوتونها امری سادهتر نسبت به دیگر روشها است. البته از مشکلات سیستمهای اپتیکی میتوان به نبود منبع تک فوتون ایدهآل و همچنین احتمالی بودن برهمکنش فوتونها در صورت نیاز، با یکدیگر اشاره کرد.

کیوبیتها نیز همانند بیتها به وسیله گیتها پردازش میشوند که در دنیای فیزیک کوانتوم به گیتهای کوانتومی معروفاند. یک گیت کوانتومی در واقع همان اپراتور یا عملگری یکانی تحول زمانی در فیزیک کوانتوم است که با ماتریسهای مربعی نمایش داده میشوند. جهت آشنایی با یکی از معروفترین گیتهای برگشتپذیر کوانتومی، به مقاله «گیت برگشتپذیر توفولی (CCNOT) -- به زبان ساده» مراجعه کنید. پیادهسازی گیتهای کوانتومی و در ادامه الگوریتم و مدارهای کوانتومی به سادگی کار با بیت و مدارات منطقی کلاسیکی نبوده و بسیار دشوار است. اما تا به امروز روشهایی برای پیادهسازی گیتهای کوانتومی با استفاده از اپتیک خطی و غیرخطی ارائه شده است. همچنین الگوریتم کوانتومی «گراور» (Grover) برای جستوجو در پایگاههای داده نیز توسط «محاسبات کوانتومی با اپتیک خطی» (Linear Optical Quantum Computing - LOQC) پیادهسازی شده است. امید است که در آیندهای نزدیک شاهد تجاریسازی کامپیوترهای کوانتومی باشیم.
در صورت علاقهمندی به مباحث مرتبط در زمینه فیزیک و کامپیوتر، آموزشهای زیر نیز به شما پیشنهاد میشوند:
- مجموعه آموزشهای فیزیک
- مجموعه آموزشهای دروس علوم و مهندسی کامپیوتر
- درهم تنیدگی کوانتومی -- به زبان ساده
- فوتون در فیزیک — به زبان ساده
- پلاریزاسیون — به زبان ساده
- سیستمهای باینری به زبان ساده – بخش اول: اعداد باینری
- منطق دیجیتال — از صفر تا صد
^^













با سلام. میشه تعیین زمان همدوسی اسپین الکترون رو هم توضیح بدید؟
میشه منبع مطالبی که می نویسید را هم اضافه کنید
با سلام؛
منبع تمامی مطالب مجله فرادرس اگر ترجمه باشند در انتهای مطلب و پیش از نام نویسنده آورده شدهاند.
با تشکر از همراهی شما با مجله فرادرس