فضای متریک و نامساوی مثلثی – به زبان ساده
فضایهای متریک و البته ورامتریک در ریاضیات بخصوص در نظریههای اندازه و تعیین فاصله بین نقاط به کار میرود. از طرفی نامساوی مثلثی و شکلهای مختلف آن در حالت چند بُعدی نیز بخصوص در فیزیک مدرن و نظریه نسبیت مورد توجه هستند. شاید بتوان ایدههای اصلی نظریه نسبیت عام اینشتین را برگرفته از فضاهای متریک معرفی شده توسط مینکوفسکی دانست. به همین علت در این نوشتار به بررسی فضای متریک و نامساوی مثلثی خواهیم پرداخت و با ذکر تعاریف و کاربردهای مربوط به این مبحث، مفاهیم اولیه را فرا خواهیم گرفت.
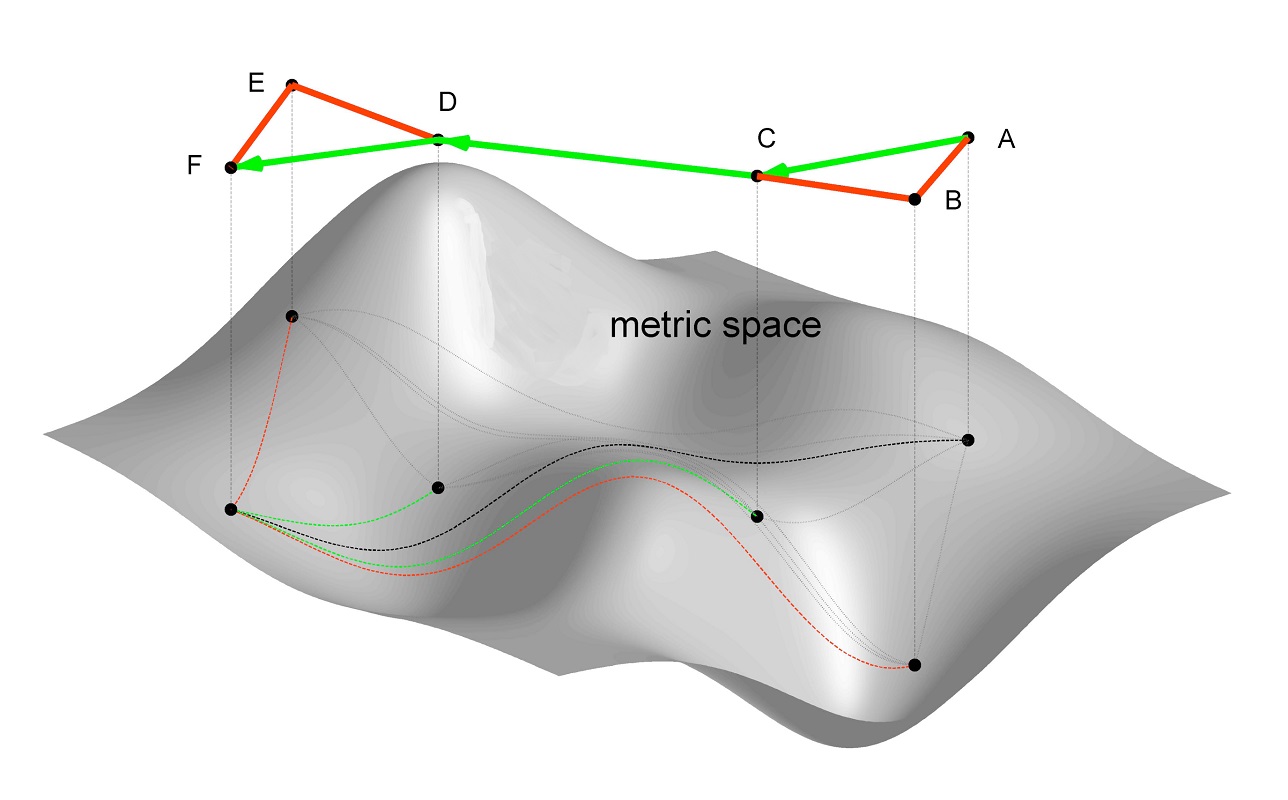


فضای متریک و نامساوی مثلثی
از آنجایی که در این نوشتار به دفعات زیاد از اصطلاح فضای متریک صحبت میشود، بهتر است با آن بیشتر آشنا شویم. در ادامه با فضای ورامتریک نیز آشنا شده و خواص هر یک را با هم مقایسه خواهیم کرد. این مفاهیم بخصوص در مباحث مربوط به تعیین فاصله و خوشهبندی در یادگیری ماشین به کار گرفته میشوند.
فضای متریک
همان طور که در نوشتار معادله و نامعادله در ریاضی — پیدایش و کاربردها بیان شد، شاید یکی از اختراعات بسیار موثر و بیمانند بشر را بتوان اعداد، شمارش و به کار بردن محاسبات روی اعداد در نظر گرفت. با قدرت گرفتن ذهن بشر برای درک ناشناختهها، قدرت تحلیل او نیز افزایش یافته و سعی کرده تا مسائل حل شده گذشته را در فضاها یا موقعیتها جدید نیز به کار گرفته، تعمیم دهد. فضای متریک نیز حاصل این عمل است.
فضای متریک در ریاضیات شامل یک مجموعه به همراه یک تابع فاصله است که روی این مجموعه قابل استفاده است. منظور از تابع فاصله، تابعی است که میتوان مقدار آن را فاصله بین دو عضو از مجموعه در نظر گرفت. گاهی به اعضای چنین مجموعهای، نقطه گفته میشود. فرض کنید مجموعه با تابع فاصله تشکیل یک فضای متریک بدهند. آنگاه خواص زیر برای اعضای مجموعه برحسب تابع وجود دارد.
- فاصله هر نقطه از مجموعه با خودش برابر با صفر است.
- فاصله بین دو نقطه مجزا از مجموعه ، مثبت است. بنابراین تابع تابعی، مثبت مقدار است.
- فاصله بین دو نقطه و برابر با فاصله بین دو نقطه و است. به این ترتیب تقارن در تعیین فاصله بین دو نقطه وجود دارد.
- برای سه نقطه ، و از مجموعه ، نامساوی مثلثی (Triangle Inequality) برقرار است.
به منظور یادآوری نامساوی مثلثی را برای این سه نقطه به صورت زیر مینویسیم.
این نامساوی برای هر جایگشت از این سه نقطه نیز برقرار است. مثلا برای سه نقطه و و همچنین ، نامساویهای زیر نیز همزمان با نامساوی بالا برقرار هستند.
برای مشاهده نحوه اثبات نامساوی مثلثی در هندسه مسطحه بهتر است مطلب نامساوی مثلثی — به زبان ساده را مشاهده کنید. این اثبات بوسیله قضیه فیثاغورس و اتحادها صورت گرفته است.
البته این تعریف به صورت عکس نیز برقرار است. به این معنی که اگر مجموعه با تابع با خواص بالا موجود باشد، یک فضای متریک تشکیل شده است.
نکته: گاهی برای تابع و فضای متریک، فقط شرط اول، سوم و چهارم را در نظر میگیرند و نشان میدهند که شرط دوم نیز به خودی خود برقرار است، زیرا:
واضح است که رابطه اول براساس نامساوی مثلثی نوشته شده است. همچنین رابطه دوم نیز به کمک متقارن بودن تابع فاصله بدست آمده است. در مبحث توپولوژی به کمک تعریف فضای متریک میتوان مجموعههای باز (Open Set) و بسته (Close Set) را نیز در فضاهای توپولوژیک تعریف و اشاعه داد. در مباحث و نوشتارهای دیگر در ریاضیات در مورد فضای توپولوژیک نیز صحبت خواهیم کرد.
یکی از فضاهای متریک معروف، فضای سه بُعدی اقلیدسی () است که شامل طول، عرض و ارتفاع است. در حقیقت فضای متریک، تعمیمی بر فضای اقلیدسی است که در چهار شرط بالا صدق میکند.
در هندسه اقلیدسی، کوتاهترین فاصله بین دو نقطه، یک خط راست است. در حالیکه در هندسه بیضیگون و هندسی هذلولوی چنین چیزی برقرار نیست و کوتاهترین فاصله ممکن است توسط یک منحنی مشخص شود. اغلب چنین فضاهای هندسی را به نام فضاهای نااقلیدسی میشناسند. در این صورت استفاده از هندسههای نااقلیدسی و فضاهای متریک ضروری به نظر میرسند.
چند مثال از فضای متریک
در ادامه با چند فضای متریک آشنا میشویم که شاید در زندگی روزمره نیز به کار گرفته شوند.
- مجموعه اعداد حقیقی با متر قدر مطلق تفاضل تشکیل یک فضای متریک میدهد.
- مجموعه اعداد حقیقی مثبت با تابع فاصله نیز تشکیل یک فضای متریک میدهد.
- مجموعه بردارهای بُعدی با فاصله منهتن (Manhattan Distance Function) تشکیل یک فضای متریک میدهند.
- مجموعه بردارهای بُعدی با فاصله اقلیدسی (Euclidean Distance Function) تشکیل یک فضای متریک میدهند.
- مجموعه بردارهای بُعدی با فاصله مینکوفسکی (Minkowski Distance Function) با پارامتر تشکیل یک فضای متریک میدهند.
- مجموعه بردارهای بُعدی با فاصله چبیشف (Chebyshev Distance Function) تشکیل یک فضای متریک میدهند.
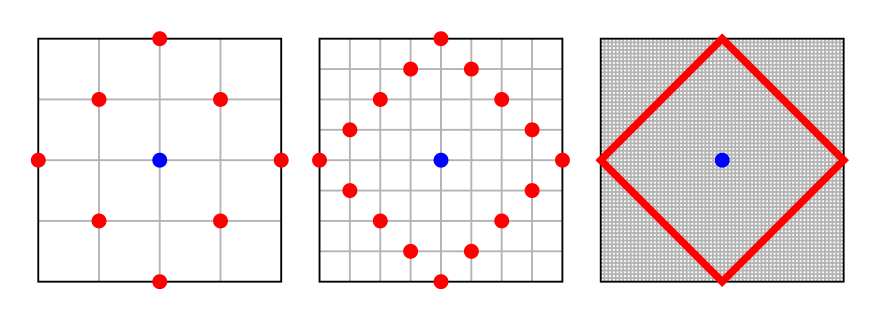
نکته: فاصله مینکوفسکی به ازاء در شرط نامساوی مثلثی صدق نمیکند، بنابراین به کمک آن نمیتوان یک فضای متریک ایجاد کرد.
نامساوی مثلثی و نرمها یا طول بردارها
تابع فاصله در فضای چند بُعدی و برداری را گاهی نُرم (Norm) نیز مینامند. به این ترتیب اندازه یا طول یک بردار توسط تابع فاصله تعیین میشود. گاهی فاصله یا نرم اقلیدسی را با و فاصله منهتن را با نشان میدهند. در حالت کلی فاصله مینکوفسکی نیز به صورت نرم مشخص میشود. در حالت چند بُعدی میتوان تعریف و خصوصیات نُرم را به صورت زیر بیان کرد.
تعریف: فضای برداری را در نظر بگیرید. یک نرم، تابعی مانند است که حقیقی مقدار روی بوده و ویژگیهای زیر را دارد:
برای هر بردار و در فضای برداری داریم:
مشخص است که نامساوی اول همان رابطه مثلثی برای توابع فاصله است که برای نرمها نیز بیان شده است. رابطه دوم نیز مقیاسپذیری نرمها است. در انتها نیز مشخص میشود که اگر طول یک بردار صفر باشد، حتما بردار نیز همه درایههایش صفر است.
برای نمایش نرمها از علامت استفاده میشود. برای مثال نمایش طول یا اندازه بردار بُعدی با نشان داده شده و به شکل زیر محاسبه میشود:
با توجه به رابطه بالا مشخص است که نرم اقلیدسی همان فاصله اقلیدسی بردار از مرکز مختصات است. به همین ترتیب میتوان نرم یا همان فاصله منهتن را برای بردار نیز تعریف کرد.
در نهایت نرم که با همان خصوصیات فاصله مینکوفسکی مطابقت دارد به شکل زیر تعریف و محاسبه میشود.
نکته: البته توجه داشته باشید که در اینجا نیز و برای های کوچکتر از ۱ رابطه بالا یک نرم ایجاد نمیکند.
زمانی که به سمت بینهایت برود، نرم حداکثر یا همان فاصله چبیشف به صورت زیر معرفی میشود.
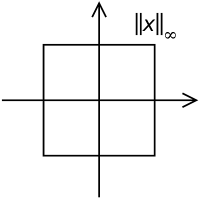
به منظور نمایش نامساوی مثلثی در حالتی که از نرمها در یک فضای برداری استفاده میشود، میتوان رابطه زیر را نوشت:
این نامساوی بیان میکند که طول مجموع دو بردار حتما از مجموع طول آن بردارها کوچکتر یا مساوی است. اگر نرم اقلیدسی در نظر گرفته شود، تساوی زمانی رخ میدهد که براساس و و همچنین مجموعشان نتوان یک مثلث تشکیل داد. به این معنی که یا باشد یا یا با شرط . البته این وضعیت را برای فاصله منهتن یا نرم نمیتوان در نظر گرفت زیرا با توجه به دو نقطه و داریم:
در حالیکه میتوان با این دو نقطه و مجموعشان یک مثلث تشکیل داد و در عین حال نامساوی تبدیل به تساوی شود.
نامساوی مثلثی معکوس
همان طور که دیده شد، نامساوی مثلثی یک کران بالا برای طول مجموع دو بردار را مشخص میکند. نوع دیگری از نامساوی مثلثی نیز وجود دارد که کران پایین برای اندازه یا طول جمع دو بردار را بیان میکند.
در هندسه مسطحه (در مقابل هندسه هذلولوی) نامساوی مثلثی به صورت زیر خوانده میشود:
طول هر ضلع از مثلث، از مجموع دو ضلع دیگر کوچکتر است.
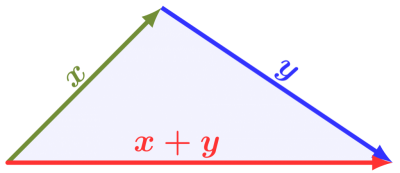
این گزاره در رابطه پایین کاملا مشهود است. بنابراین یک کران بالا برای طول بردار حاصل از جمع دو بردار مشخص شد.
حال سعی میکنیم یک کران پایین برای طول بردار پیدا کنیم. باز هم در هندسه مسطحه میتوان گزاره زیر را در نظر گرفت.
طول هر ضع از مثلث، از تفاضل دو ضلع دیگر بزرگتر است.
بنابراین میتوان قضیه زیر را برای بردارها نیز بیان کرد.
قضیه: برای دو بردار و با نرم داریم:
اثبات: برای اثبات قضیه نامساوی مثلثی معکوس کافی است از نامساوی مثلثی استفاده کنیم، توجه داشته باشید که بین نرم تفاضل دو بردار رابطه زیر برقرار است:
به این ترتیب میتوان نوشت:
و
در نتیجه با ترکیب این دو عبارت، قضیه اثبات خواهد شد.
فضای ورامتریک
در فضای متریک، وجود رابطه مثلثی از مهمترین خصوصیات محسوب میشود. ولی در فضای ورامتریک (UltraMetric)، رابطه مثلثی به شکل دیگری نمایش داده میشود که در ادامه قابل مشاهده است.
فرض کنید و و سه نقطه در فضای بُعدی باشند.
به بیان دیگر این رابطه نشان میدهد که فاصله بین دو نقطه با از حداکثر فاصله بین نقطه با و با کوچکتر یا مساوی است. تابع با چنین خاصیتی را یک تابع ورامتر نامیده و فضای حاصل از یک مجموعه و چنین تابعی را یک فضای ورامتریک مینامند.
با استفاده از نرمها و فضای برداری میتوان فضای ورامتریک را براساس رابطه زیر مشخص کرد.
پس تساوی در این جا، در حالتی رخ میدهد که طول دو بردار یکسان نباشد. به منظور اثبات این قضیه به صورتی که در ادامه قابل مشاهده است، عمل میکنیم.
بدون آنکه حالت کلی را نقض کنیم، فرض کنید طول بردار از بیشتر است.
در نتیجه طبق رابطه ورامتر بودن نرم خواهیم داشت:
از طرفی برای نرم بردار میتوان نوشت:
چون بیشترین طول در بین این دو بردار مربوط به بردار در نظر گرفته شده است پس مقدار حداکثر رابطه بالا نمیتواند باشد. در نتیجه:
و همچنین
در نتیجه براساس رابطه ورامتر و رابطه بالا خواهیم داشت:
در هندسه مسطحه براساس مثلثها میتوان گفت که خاصیت ورامتر فقط برای مثلث متساویالساقین و متساویاضلاع برقرار است و شکلهای دیگر مثلثی، این خاصیت را نخواهند داشت.
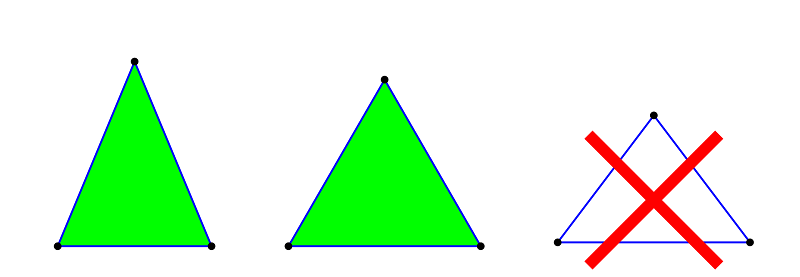
به این ترتیب حداقل باید یکی از تساویها زیر برقرار باشد تا فضای ورامتریک حاصل شود.
یا
یا
رابطه فضای ورامتریک و متریک
فرض کنید یک فضای ورامتریک باشد. نشان میدهیم که این فضا یک فضای متریک نیز هست. طبق رابطه ورامتر برای تابع داریم:
پس:
رابطه ۱
یا
رابطه ۲
فرض کنید که رابطه ۱ برقرار باشد. از آنجایی که تابع فاصله نامنفی است پس اضافه کردن یک جمله مثبت به سمت راست این رابطه نامساوی را تغییر نمیدهد.
همین عمل را نیز با فرض صحیح بودن رابطه ۲ میتوان نوشت. در نتیجه میتوان گفت که یک فضای ورامتریک حتما یک فضای متریک نیز هست ولی عکس آن برقرار نیست. در حقیقت شرط ورامتر بودن برای تابع ، قویتر نسبت به شرط نامساوی مثلثی است.
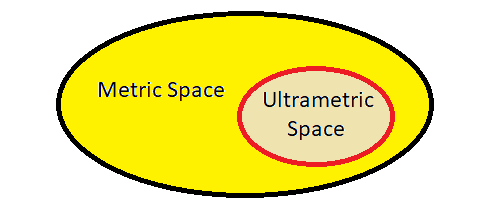
از توابعی که خاصیت ورامتر دارند اغلب برای سنجش فاصله در خوشهبندی مشاهدات استفاده میشود و گاهی به خاصیت نامساوی آنها نامساوی قوی گفته میشود.
کاربردهای فضای ورامتریک
به منظور سنجش فاصله بین دو نقطه در حالتی که متغیر یا ویژگیها، کیفی باشند معمولا از میزان یا درصد عدم انطباق استفاده میشود. این تابع برای هر ویژگی به صورت زیر تعریف میشود.
$$\large \rho (x,y)=\left\{{\begin{matrix}1&{\mbox{if}}\ x\neq y,\\0&{\mbox{if}}\ x=y\end{matrix}}\right.$$
واضح است که اگر یک مولفه در بین دو بردار مشاهدات یکسان باشند مقدار برابر با ۱ خواهد بود و در غیر اینصورت مقدار صفر خواهد داشت. چنین تعریفی برای فاصله، یک فضای ورامتریک تولید خواهد کرد که به آن فضای گسسته (Discrete Space) میگویند.
این تابع فاصله در خوشهبندی دادههای کیفی بسیار به کار میرود. البته عکس این رابطه نیز به عنوان تابع شباهت استفاده میشود که به درصد انطباق ساده معروف است.
$$\large s (x,y)=\left\{{\begin{matrix}1&{\mbox{if}}\ x = y,\\0&{\mbox{if}}\ x\neq y\end{matrix}}\right.$$
نوع دیگری از این روش اندازهگیری شباهت یا فاصله نیز به شباهت ژاکارد و یا فاصله ژاکارد شهرت دارد.
در صورتی که مطلب بالا برای شما مفید بوده است، آموزشهای زیر نیز به شما پیشنهاد میشوند:
- مجموعه آموزشهای ریاضی
- مجموعه آموزشهای فیزیک
- نامساوی شوارتز — به زبان ساده
- رسم نامعادلات و نامساوی های خطی — به زبان ساده
- اثبات نامساوی با مشتق — به زبان ساده
^^














