ماتریس خلوت در ریاضیات و ساختمان داده | به زبان ساده

یکی از مباحث مربوط به آنالیز عددی (Numerical Analysis) که جنبه کاربردی در علوم محاسباتی بخصوص در برنامه‌نویسی رایانه‌ای دارد، ماتریس خلوت (Sparse Matrix) یا بردار خلوت (Sparse Array) است. شیوه‌های مختلفی برای نمایش یا بیان ماتریس‌های خلوت وجود دارد که کارایی محاسبات بیشتری نسبت به ماتریس‌های اصلی دارند. از این جهت که محاسبات ماتریسی و برداری، براساس این گونه نمایش ماتریس‌های خلوت، ساده‌تر و موثرتر هستند، در این نوشتار به بررسی ماتریس خلوت در ریاضیات و کاربردهای آن در ساختمان داده خواهیم پرداخت.

برای آشنایی بیشتر با ماتریس‌ها بهتر است نوشتارهای ماتریس‌ها در ریاضی — به زبان ساده و ترانهاده ماتریس — به زبان ساده را مطالعه کنید. همچنین خواندن مطالب ساختمان داده (Data Structure) — راهنمای جامع و کاربردی و دترمینان یک ماتریس — به زبان ساده  نیز خالی از لطف نیست.

ماتریس خلوت در ریاضیات و ساختمان داده

می‌دانید که ماتریس (Matrix) یک نمای دو بعُدی از داده‌ها است، بطوری که به شکل یک جدول با $$n$$ سطر و $$m$$ ستون قابل نمایش باشد. مقدارهای درون این جدول، درایه‌های ماتریس گفته شده و می‌توانند در مجموعه اعداد حقیقی (زمانی که موضوع یا زمینه کاری اعداد حقیقی است) تغییر کنند. البته امکان استفاده از مقادیر یا اعداد مختلط نیز در ماتریس‌ها وجود دارد.

فیلم آموزش ساختمان داده ها – مرور و تست کنکور ارشد در فرادرس

کلیک کنید

اغلب با توجه به ابعاد ماتریس‌ها، آن‌ها را شناسایی و طبقه‌بندی می‌کنیم. در زیر یک ماتریس با ۳ سطر و ۲ ستون را مشاهده می‌کنید.

$$ \large \begin{bmatrix}1 & 5 \\ 3 & 1.2 \\ -6 & \sqrt{12} \end{bmatrix} $$

معمولا درایه‌های یک ماتریس $$n \times m$$ را به صورت زیر مشخص می‌کنند.

$$ \large [a_{ij}] , \;\;i= 1 , \ldots , n , \;\;\; j = 1, \ldots,  m $$

این ساختار یک ماتریس را نشان می‌دهد. در این حالت $$i$$ را اندیس سطر (Row Index) و $$j$$ را اندیس ستون (Column Index) می‌نامیم.

نکته: فضای ذخیره سازی برای چنین ماتریسی در حافظه رایانه‌ها، متناسب با تعداد سطرها و ستون‌ها خواهد بود. در نتیجه هر چه ماتریس دارای ابعاد بزرگتری باشد، فضای ذخیره‌سازی بیشتری نیز در حافظه احتیاج دارد.

حال یک ماتریس به صورت زیر را در نظر بگیرید.

$$ \large S = \begin{bmatrix}0 & 1 & 0 \\ 0 & 0 & 0\\ -6 & \sqrt{12} & 0 \\ 0 & -1 &0 \\ 0 & 0 & 2 \end{bmatrix} $$

در این حالت، ماتریس A را یک «ماتریس خلوت» (Sparse Matrix) یا ماتریس پراکنده می‌نامند، زیرا درایه‌های موثر (تغییر پذیر) آن نسبت به درایه‌های صفر (ثابت) بیشتر است. در مقابل اگر درایه‌های موثر یک ماتریس بیش از درایه‌های صفر آن باشند، ماتریس را «ماتریس متراکم» (Dense Matrix) می‌گویند.

مشخص است که بسیاری از عناصر یا درایه‌های ماتریس خلوت صفر (یا ثابت) هستند. در نتیجه ذخیره سازی چنین ماتریسی به شکل کامل، حافظه نسبتا زیادی را با توجه به اطلاعات موجود در ماتریس اصلی خواهد گرفت. از طرفی بار محاسباتی نیز برای ماتریس‌هایی به این شکل، زیاد خواهد بود در حالیکه برای مثلا ضرب، بیشتر محاسبات یکسان در نظر گرفته می‌شوند.

توجه داشته باشید که ماتریس‌های مربعی از نوع «بالا مثلثی» (َUpper Triangular) یا «پایین مثلثی» (Lower Triangular) یا «ماتریس قطری» (Diagonal Matrix)، ماتریس‌های خلوت محسوب می‌شوند.

نکته: اگر ماتریس‌های خلوت به جای مقدار صفر، یک مقدار ثابت دیگر داشته باشند، نحوه ذخیره‌سازی آن‌ها باز هم می‌تواند به شیوه بیان ماتریس‌های خلوت باشد. فقط هنگام انجام عملیات ریاضی، باید با دقت بیشتری نسبت به محاسبات عمل کرده و اثر این مقدار ثابت را در محاسبات بعدی لحاظ کنیم.

چنین وضعیتی برای بسیاری از ساختارهای ذخیره سازی ممکن است رخ دهد. برای مثال تصویری از یک نوشته که زمینه‌ای سیاه دارد، دارای مقدارهای زیادی از کد مثلا صفر برای نمایش رنگ زمینه است. اگر قرار باشد که همه این پیکسل‌های تصویری ذخیره شوند، حجم زیادی از حافظه اشغال خواهد شد. در حالیکه فقط بعضی از پیکسل‌ها اهمیت داشته و مقادیر متفاوتی دارند.

بنابراین شیوه‌ای برای ذخیره سازی چنین ماتریس‌هایی در حوزه مباحث مربوط به «ساختمان داده» (Data Structure) مطرح می‌شود که در ادامه به این موضوع خواهیم پرداخت. البته این تکنیک‌ها به کاهش حجم و فشرده‌سازی مقادیر و ماتریس‌ها کمک کرده و می‌توانند برای فشرده کردن تصویرهای بیتی (Bitmap Image) به کار روند.

ضریب خلوتی (Sparsity)

یک ماتریس خلوت (Sparse Matrix)، به ماتریسی گفته می‌شود که دارای درایه صفر (یا ثابت) زیادی باشد. در این حالت می‌توان برای چنین ماتریس‌هایی «ضریب خلوتی» (Sparsity) را به شکل نسبت درایه‌های غیر صفر به کل درایه‌ها در نظر گرفت. به این ترتیب فرمول زیر را برای محاسبه ضریب خلوتی خواهیم داشت.

$$ \large Sparsity = \dfrac{ \text{# of non-zero elements} }{ \text{# of total elements} } $$

فیلم آموزش ساختمان داده ها در فرادرس

کلیک کنید

به این ترتیب برای ماتریس S‌ که در بالا معرفی شد، مقدار ضریب خلوتی برابر است با:

$$ \large Sparsity(S) = \dfrac{10}{15}  = \dfrac{1}{3} = 0.67 $$

همچنین اگر ماتریس خلوتی را به شکل زیر در نظر گرفته باشیم،

$$ \large \begin{pmatrix} 11 & 22 & 0 & 0 & 0 & 0 & 0 \\ 0 & 33 & 44 & 0 & 0 & 0 & 0 \\ 0 & 0 & 55 & 66 &  77 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 & 88 & 0 \\  0 & 0 & 0 & 0 & 0 & 0 & 99 \end{pmatrix} $$

ضریب خلوتی برای آن به صورتی که در ادامه قابل مشاهده است، قابل محاسبه است.

$$ \large Sparsity= \dfrac{26}{35}  = 0.74 $$

واضح که ماتریس بالا، دارای ضریب خلوتی بزرگتری نسبت به ماتریس S است، در نتیجه فضای کمتری برای ذخیره‌سازی آن لازم خواهد بود. متمم ضریب خلوتی، به ضریب تراکم یا «چگالی» (Density) معروف است. مشخص است که برای ماتریس بالا، ضریب چگالی برابر با مقدار زیر است.

$$ \large Density =1 - Sparsity = 1 -  0.74  = 0.26 = \dfrac{9}{35}$$

همچنین برای ماتریس S نیز چگالی برابر است با:

$$ \large Density(S) = 1 -  Sparsity = 1 -  0.67  = 0.33 = \dfrac{5}{15}$$

حال یک ماتریس ۲۰۰۰ در ۲۰۰۰ را در نظر بگیرید که فقط ۵۰۰ مقدار آن، مخالف صفر است. مقدار ضریب خلوتی آن برابر  0٫999 قرار دارد. واضح است که ذخیره سازی چهار میلیون مقدار که فقط ۵۰۰ تای آن مخالف صفر است، فضای بسیار بیشتری نسبت به حالتی خواهد داشت که ماتریس خلوت را با شیوه‌های فشرده‌سازی و با ساختاری دیگر ذخیره کنیم. در زیر ضریب خلوتی و چگالی این چنین ماتریسی را محاسبه کرده‌ایم.

$$ \large Sparsity= \dfrac{3999500}{4000000}  = 0.9999 $$

$$ \large Density= \dfrac{500}{4000000}  = 0.0001 $$

ذخیره سازی یک ماتریس خلوت

در مورد یک ماتریس خلوت یا پراکنده، می‌توان با ذخیره کردن فقط ورودی‌های غیر صفر عمل ثبت را انجام داد و با این کار کاهش حافظه قابل توجهی برای ذخیره سازی این ساختار بوجود آورد. بسته به تعداد و پراکندگی ورودی‌های غیر صفر ماتریس خلوت، از ساختار داده‌های مختلفی می‌توان استفاده کرد و در مقایسه با ثبت کامل ماتریس، صرفه جویی زیادی در حافظه صورت داد.

نکته: مهم این است که در ساختار جدید ممکن است دسترسی به عناصر خاص، پیچیده‌تر شود و ساختارهای اضافه‌ای لازم خواهد بود تا بتوانیم ماتریس اصلی را به صورت کامل بازیابی کنیم.

در کل می‌توان شیوه یا ساختار ذخیره سازی ماتریس خلوت را به دو دسته تقسیم کرد.

• روش‌هایی که از پشتیبانی خوبی برای تغییرات روی درایه‌های ماتریس اولیه برخوردار هستند. مانند «کلیدهای دیکشنری» (Dictionary of Keys) که به اختصار KOD گفته می‌شوند. یا روش «لیستی از لیست‌ها» (List of Lists)  که به صورت خلاصه به شکل LIL نشان داده شده، یا «لیست مختصات» (Coordinate List) با عبارت اختصاری COO، همگی روش‌هایی برای نمایش یک ماتریس خلوت هستند.
• رویکرد دیگر برای نمایش ماتریس خلوت، تکنیک CSR یا «ردیف خلوت فشرده» (Compressed Sparse Row) یا CSC یا «ستون خلوت فشرده» (Compressed Sparse Column) است که برای اجرای عملیاتی مانند ترانهاده کردن ماتریس اولیه، بسیار کارا عمل می‌کنند.

ابتدا شیوه اول را معرفی کرده، سپس روش CSR را به کار می‌بریم.

رویکرد COO برای نمایش ماتریس خلوت

اغلب برای نمایش ساختار مختصاتی یا لیست مختصات از شکل زیر (که ظاهری مانند ماتریس دارد) استفاده می‌کنند. توجه داشته باشید که ردیف اول به ویژگی‌های ماتریس خلوت پرداخته و ارتباط با مقدارها ندارد.

• ردیف اول: ابتدا تعداد سطرها، سپس تعداد ستون‌ها و در انتها نیز تعداد عناصر غیر صفر مشخص می‌شود.
• ردیف‌های بعدی: به ترتیب شماره سطر، شماره ستون و مقدار عنصر غیر صفر از ماتریس خلوت قرار می‌گیرد.

از آنجایی که، نحوه نوشتن مقادیر سطر به سطر صورت خواهد گرفت، ستون اول این شیوه نمایش، از کوچک به بزرگ مرتب شده است (بدون توجه به سطر اول).

یک ماتریس، مربعی $$ 4 \times 4$$ با ۴ عنصر غیر صفر به صورت زیر را در نظر بگیرید.

$$ \large {\begin{pmatrix} 0 & 0 & 0 & 0 \\ 5 & 8 & 0 & 0 \\ 0 & 0 & 3 & 0 \\ 0 & 6 & 0 & 0 \\ \end{pmatrix}} $$

با استفاده از شیوه COO، نمایش ماتریس خلوتی که در بالا معرفی شد، به صورت زیر خواهد بود.

$$ \large \begin{bmatrix} 4 & 4 & 4 \\  \hline
1 & 0 & 5 \\
1 & 1 & 8 \\
2 & 2 & 3 \\
3 & 1 & 6 \\
\end{bmatrix} $$

ساختار ردیف خلوت فشرده

در این قسمت با توجه به تکنیک به کار رفته در «ردیف خلوت فشرده» (Compressed Sparse Row) یا به اختصار CSR به این شیوه ذخیره سازی یک ماتریس خلوت خواهیم پرداخت تا بتوانیم محاسبات دیگری مانند جمع و ترانهاده ماتریس را نیز به کمک بیان فشرده ماتریس خلوت انجام دهیم.

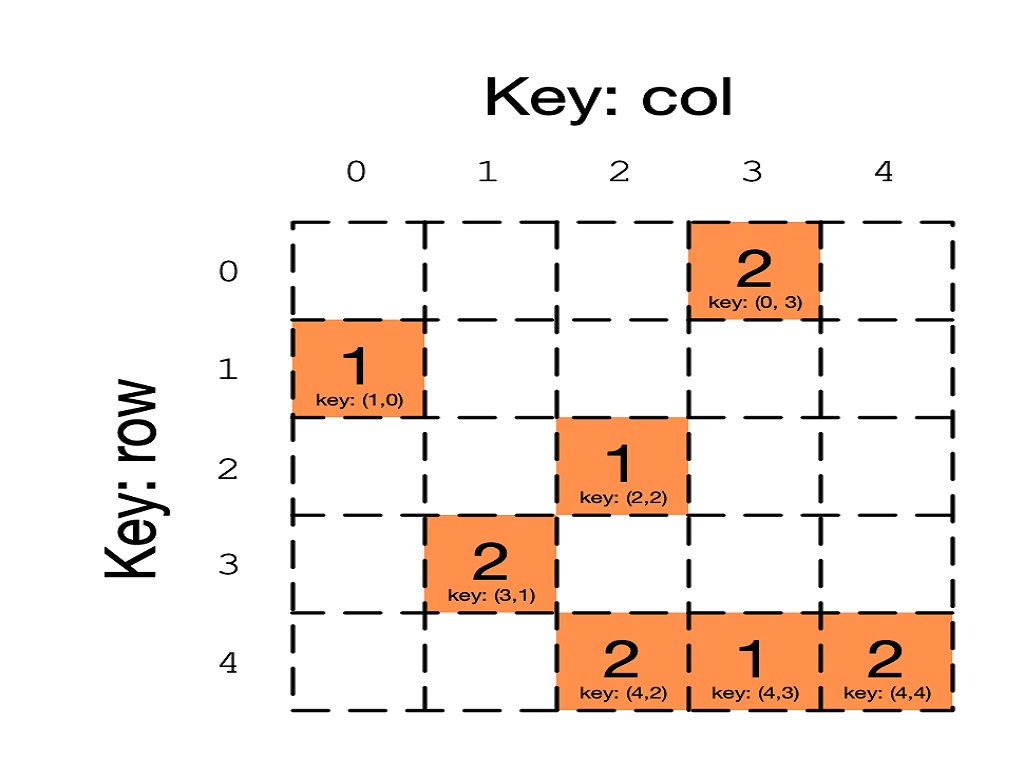
این شیوه بیان ماتریس خلوت، از یک بردار سه بعدی (سه تایی مرتب) استفاده می‌کند. گاهی به این شیوه بیان ماتریس خلوت، «قالب یل» (Yale Format) نیز می‌گویند. به این ترتیب برای هر درایه غیر صفر، شماره ردیف و ستون ماتریس، به همراه مقدار آن درایه، ثبت شده و هر سطر، تشکیل یک سه تایی مرتب (Triple) را می‌دهد. این سه‌تایی‌های مرتب را در سه بردار می‌توان ذخیره کرد. این بردارها را به صورت زیر نام‌گذاری می‌کنند.

• V یا Value: مقدار درایه را مشخص می‌کند. واضح است که این مقدار غیر صفر است.
• Col_index: شماره ستون مربوط به مقدار درایه را در ماتریس اولیه تعیین می‌کند.
• Row_index: شماره ردیف درایه مورد نظر در این قسمت ثبت می‌شود.

ماتریس زیر را در نظر بگیرید. واضح است که این ماتریس، مربعی $$ 4 \times 4$$ بوده که فقط ۴ عنصر آن غیر صفر است.

$$ \large {\begin{pmatrix} 0 & 0 & 0 & 0 \\ 5 & 8 & 0 & 0 \\ 0 & 0 & 3 & 0 \\ 0 & 6 & 0 & 0 \\ \end{pmatrix}} $$

بیان این ماتریس خلوت به شیوه CSR، به شکل زیر خواهد بود. سه آرایه کاملا در این شکل از نمایش ماتریس خلوت دیده می‌شود.

1 V         = [ 5 8 3 6 ]
2   COL_INDEX = [ 0 1 2 1 ]
3   ROW_INDEX = [ 0 0 2 3 4 ]

نکته: فرض بر این است که اندیس اول در اینجا با صفر نشان داده شده است.

در ادامه کدی را با زبان برنامه‌نویسی ++C‌ مشاهده می‌کنید که به تبدیل ساختار آرایه‌ای (سه تایی مرتب) از ماتریس خلوت می‌پردازد.

فیلم آموزش برنامه نویسی C++‎ سی پلاس پلاس در فرادرس

کلیک کنید

ماتریس مورد نظر برای تبدیل به نمایش سطر خلوت فشرده به صورت زیر مشخص شده است.

$$ \large \begin{pmatrix}
0 & 0 & 0 & 0 & 9 & 0 \\
0 & 8 & 0 & 0 & 0 & 0 \\
4 & 0 & 0 & 2 & 0 & 0 \\
0 & 0 & 0 & 0 & 0 & 5 \\
0 & 0 & 2 & 0 & 0 & 0 \\
\end{pmatrix} $$

1#include<iostream>
2
3using namespace std;
4
5int main()
6{
7    // sparse matrix of class 5x6 with 6 non-zero values
8    int sparseMatrix[5][6] =
9    {
10        {0 , 0 , 0 , 0 , 9, 0 },
11        {0 , 8 , 0 , 0 , 0, 0 },
12        {4 , 0 , 0 , 2 , 0, 0 },
13        {0 , 0 , 0 , 0 , 0, 5 },
14        {0 , 0 , 2 , 0 , 0, 0 }
15    };
16
17    // Finding total non-zero values in the sparse matrix
18    int size = 0;
19    for (int row = 0; row < 5; row++)
20        for (int column = 0; column < 6; column++)
21            if (sparseMatrix[row][column] != 0)
22                size++;
23
24    // Defining result Matrix
25    int resultMatrix[3][size];
26
27    // Generating result matrix
28    int k = 0;
29    for (int row = 0; row < 5; row++)
30        for (int column = 0; column < 6; column++)
31            if (sparseMatrix[row][column] != 0)
32            {
33                resultMatrix[0][k] = row;
34                resultMatrix[1][k] = column;
35                resultMatrix[2][k] = sparseMatrix[row][column];
36                k++;
37            }
38
39    // Displaying result matrix
40    cout<<"Triplet Representation : "<<endl;
41    for (int row=0; row<3; row++)
42    {
43        for (int column = 0; column<size; column++)
44            cout<<resultMatrix[row][column]<<" ";
45
46        cout<<endl;
47    }
48    return 0;
49}

حاصل اجرای این برنامه و خروجی بدست آمده، به صورت زیر خواهد بود.

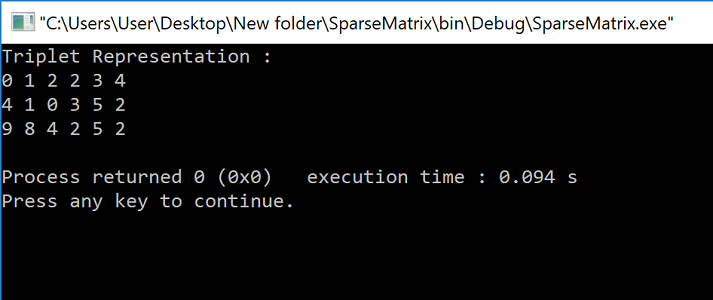
همانطور که می‌بینید، شیوه ارائه ماتریس خلوت مطابق با نحوه نمایش سطر خلوت فشرده است. در ادامه طبق این شیوه نمایش، محاسباتی نظیر پیدا کردن ترانهاده و جمع کردن دو ماتریس خلوت خواهیم پرداخت. به یاد داشته باشید که نتیجه حاصل از محاسبات روی شیوه نمایش سطر خلوت فشرده، برای بازسازی ماتریس اصلی باید به کار رود تا نتیجه محاسبات به شکل ملموس در بیاید.

ساختار ستون خلوت فشرده

اگر برای استخراج ماتریس فشرده، مقادیر ماتریس به جای ترتیب سطری از ترتیب ستونی برخوردار باشند، روش ذخیره سازی یا ساختار داده را به صورت «ستون خلوت فشرده» (Compressed sparse column) یا به اختصار CSC می‌شناسند. به این ترتیب این بار اندیس ستون (Column Index) در ساختار جدید، مرتب شده است. ولی مقدارهای ماتریس و اندیس سطر و ستون به شیوه قبل مشخص خواهد شد.

نمایش و ثبت ماتریس خلوت در نرم‌افزار MATLAB‌ از ساختار ستون خلوت فشرده با استفاده از تابع sparse بهره می‌برد. این شیوه اغلب برای انجام محاسبات ریاضی مناسب‌تر است.

ترانهاده یک ماتریس خلوت

عملگر ترانهاده روی یک ماتریس باعث می‌شود جای مقدارهای درون سطرها با ستون‌ها عوض شود. به این ترتیب $$A$$ را یک ماتریس $$m \times n $$ با درایه‌هایی به صورت زیر در نظر می‌گیریم.

$$ \large a_{ij} , \;\;\;\; i = 1 , \dots , m ,\;\; j = 1 , \ldots , n $$

فیلم آموزش ماتریس ها و جبر خطی – حل مثال و تست کنکور کارشناسی ارشد در فرادرس

کلیک کنید

در این صورت ماتریس حاصل از عمل ترانهاده که به شکل $$A'$$ نشان داده می‌شود، دارای ابعادی به صورت $$ n \times m $$ است، بطوری که درایه‌های آن از همان درایه‌های ماتریس $$A$$ تشکیل شده ولی داریم:

$$ \large a'_{ij} = a_{ji} $$

همانطور که در ساختار سطری خلوت فشرده مشاهده کردید، مقادیری که مقدار مخالف صفر در ماتریس خلوت داشتند، با اندیس سطر و ستون و مقدار درایه ماتریس مشخص و ذخیره می‌شوند. بنابراین اگر بخواهیم چنین  ساختاری را برای ترانهاده یک ماتریس ایجاد کنیم، کافی است که مقدار اندیس سطر را با ستون تغییر دهیم.

برای مثال ماتریس زیر را در نظر بگیرید.

$$ \large A= \begin{pmatrix} 0 & 0 & 0 & 0 & 9 & 0 \\ 0 & 8 & 0 & 0 & 0 & 0 \\ 4 & 0 & 0 & 2 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 & 5 \\ 0 & 0 & 2 & 0 & 0 & 0 \\ \end{pmatrix} $$

مشخص است که ترانهاده آن به صورت زیر در خواهد آمد.

$$ \large A' = \begin{pmatrix} 0 & 0 & 4 & 0 & 0 \\ 0 & 8 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 2 \\ 0 & 0 & 2 & 0 & 0 \\ 9 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 5 & 0 \end{pmatrix} $$

ولی اینبار بدون آنکه عملگر ترانهاده را روی ماتریس $$A$$‌ اجرا کنیم، می‌خواهیم برحسب نمایش سطری فشرده، ماتریس ترانهاده $$A$$ را بدست آورده و برهمان شیوه نمایشی نیز ظاهر کنیم. به وضوح فقط کافی است در نمایش فشرده سطری، جای اندیس سطرها را با اندیس ستون‌ها عوض کنیم. در حقیقت بردار Row_index را با Column_index جابجا کنیم. به این ترتیب اگر نمایش فشرده سطری ماتریس $$A$$ به صورت زیر باشد:

1 V         = [ 9 8 4 2 5 2 ]
2   COL_INDEX = [ 4 1 0 3 5 2 ]
3   ROW_INDEX = [ 0 1 2 2 3 4 ]

ترانهاده آن نیز به شکل زیر در خواهد آمد.

1 V         = [ 9 8 4 2 5 2 ]
2   COL_INDEX = [ 0 1 2 2 3 4 ]
3   ROW_INDEX = [ 4 1 0 3 5 2 ]

برنامه زیر برای انجام این عمل تهیه شده است.

1void transpose( int bs[][3], int bt[][3])
2{
3 int i, j, k;
4 bt[0][0]=bs[0][1]; bt[0][1]=bs[0][0]; bt[0][2]=bs[0][2];
5 k=1;
6 for(i=0;i< bs[0][1];i++)
7 for(j=1; j< bs[0][2]; j++ )
8 if(i==bs[j][1])
9 {
10 bt[k][0]=bs[j][1];
11 bt[k][1]=bs[j][0];
12 bt[k][2]=bs[j][2];
13 k++;
14 }
15}

جمع دو ماتریس خلوت

این بار برای نمایش جمع دو ماتریس خلوت که به شیوه COO معرفی شده‌اند، به صورت زیر عمل می‌کنیم. البته توجه دارید که باید تعداد سطرها و ستون‌های هر دو ماتریس خلوت، برابر بوده تا قابل جمع باشند در نتیجه درایه‌های اول و دوم در سطر اول هر دو نمایش ماتریس‌ها باید یکی باشد. توجه داشته باشید که کار را به ترتیب سطرهای نمایش ماتریس خلوت آغاز می‌کنیم.

• کوچکترین اندیس سطری را در هر دو ماتریس در نظر بگیرید.
• اگر این اندیس در ماتریس دیگر نیز وجود دارد، اندیس ستون‌ها را مقایسه کنید.
• در صورت یکسان بودن اندیس سطر و ستون، مقدار هر یک از ماتریس‌ها را با یکدیگر جمع کنید و در سطر و ستون مربوط به پاسخ ماتریس جمع قرار دهید.
• در غیر اینصورت مقدار ردیف ماتریس اولیه با کمترین اندیس ستون را به عنوان نتیجه جمع در آن سطر و ستون مشخص کنید.
• سطری که عملیات روی آن صورت گرفته را در نمایش ماتریس خلوت مربوطه حذف کنید.
• عملیات را تا زمانی که همه سطرهای مربوط به نمایش ماتریس‌ها خلوت مورد بررسی قرار گرفته‌اند، تکرار کنید.

برای مثال به جمع دو ماتریس خلوت به شیوه نمایش دیکشنری به صورت زیر توجه کنید.

نکته: دو سطری که با رنگ آبی آسمانی مشخص شده‌اند، هنگام عمل جمع، مقدار صفر تولید خواهند کرد زیرا درایه‌های متناظر در هر دو ماتریس (مشخص شده توسط دایره‌های نارنجی) قرینه یکدیگر هستند و چون مقدار صفر را در نمایش ماتریس خلوت به کار نمی‌بریم، در نتیجه حاصل جمع این دو درایه در ماتریس مجموع دیده نمی‌شود.

قطعه کدی که در ادامه مشاهده می‌کنید، برای نمایش ترانهاده، جمع و ضرب دو ماتریس خلوت براساس نمایش CSR است که به زبان ++C نوشته شده.

1// C++ code to perform add, multiply 
2// and transpose on sparse matrices 
3#include <iostream> 
4using namespace std; 
5
6class sparse_matrix 
7{ 
8
9	// Maximum number of elements in matrix 
10	const static int MAX = 100; 
11
12	// Double-pointer initialized by 
13	// the constructor to store 
14	// the triple-represented form 
15	int **data; 
16
17	// dimensions of matrix 
18	int row, col; 
19
20	// total number of elements in matrix 
21	int len; 
22
23public: 
24	sparse_matrix(int r, int c) 
25	{ 
26
27		// initialize row 
28		row = r; 
29
30		// initialize col 
31		col = c; 
32
33		// initialize length to 0 
34		len = 0; 
35
36		//Array of Pointer to make a matrix 
37		data = new int *[MAX]; 
38
39		// Array representation 
40		// of sparse matrix 
41		//[,0] represents row 
42		//[,1] represents col 
43		//[,2] represents value 
44		for (int i = 0; i < MAX; i++) 
45			data[i] = new int[3]; 
46	} 
47
48	// insert elements into sparse matrix 
49	void insert(int r, int c, int val) 
50	{ 
51
52		// invalid entry 
53		if (r > row || c > col) 
54		{ 
55			cout << "Wrong entry"; 
56		} 
57		else
58		{ 
59
60			// insert row value 
61			data[len][0] = r; 
62
63			// insert col value 
64			data[len][1] = c; 
65
66			// insert element's value 
67			data[len][2] = val; 
68
69			// increment number of data in matrix 
70			len++; 
71		} 
72	} 
73
74	void add(sparse_matrix b) 
75	{ 
76
77		// if matrices don't have same dimensions 
78		if (row != b.row || col != b.col) 
79		{ 
80			cout << "Matrices can't be added"; 
81		} 
82
83		else
84		{ 
85			int apos = 0, bpos = 0; 
86			sparse_matrix result(row, col); 
87
88			while (apos < len && bpos < b.len) 
89			{ 
90
91				// if b's row and col is smaller 
92				if (data[apos][0] > b.data[bpos][0] || 
93				(data[apos][0] == b.data[bpos][0] && 
94					data[apos][1] > b.data[bpos][1])) 
95
96				{ 
97
98					// insert smaller value into result 
99					result.insert(b.data[bpos][0], 
100								b.data[bpos][1], 
101								b.data[bpos][2]); 
102
103					bpos++; 
104				} 
105
106				// if a's row and col is smaller 
107				else if (data[apos][0] < b.data[bpos][0] || 
108						(data[apos][0] == b.data[bpos][0] && 
109						data[apos][1] < b.data[bpos][1])) 
110
111				{ 
112
113					// insert smaller value into result 
114					result.insert(data[apos][0], 
115								data[apos][1], 
116								data[apos][2]); 
117
118					apos++; 
119				} 
120
121				else
122				{ 
123
124					// add the values as row and col is same 
125					int addedval = data[apos][2] + 
126								b.data[bpos][2]; 
127
128					if (addedval != 0) 
129						result.insert(data[apos][0], 
130									data[apos][1], 
131									addedval); 
132					// then insert 
133					apos++; 
134					bpos++; 
135				} 
136			} 
137
138			// insert remaining elements 
139			while (apos < len) 
140				result.insert(data[apos][0], 
141							data[apos][1], 
142							data[apos++][2]); 
143
144			while (bpos < b.len) 
145				result.insert(b.data[bpos][0], 
146							b.data[bpos][1], 
147							b.data[bpos++][2]); 
148
149			// print result 
150			result.print(); 
151		} 
152	} 
153
154	sparse_matrix transpose() 
155	{ 
156
157		// new matrix with inversed row X col 
158		sparse_matrix result(col, row); 
159
160		// same number of elements 
161		result.len = len; 
162
163		// to count number of elements in each column 
164		int *count = new int[col + 1]; 
165
166		// initialize all to 0 
167		for (int i = 1; i <= col; i++) 
168			count[i] = 0; 
169
170		for (int i = 0; i < len; i++) 
171			count[data[i][1]]++; 
172
173		int *index = new int[col + 1]; 
174
175		// to count number of elements having 
176		// col smaller than particular i 
177
178		// as there is no col with value < 0 
179		index[0] = 0; 
180
181		// initialize rest of the indices 
182		for (int i = 1; i <= col; i++) 
183
184			index[i] = index[i - 1] + count[i - 1]; 
185
186		for (int i = 0; i < len; i++) 
187		{ 
188
189			// insert a data at rpos and 
190			// increment its value 
191			int rpos = index[data[i][1]]++; 
192
193			// transpose row=col 
194			result.data[rpos][0] = data[i][1]; 
195
196			// transpose col=row 
197			result.data[rpos][1] = data[i][0]; 
198
199			// same value 
200			result.data[rpos][2] = data[i][2]; 
201		} 
202
203		// the above method ensures 
204		// sorting of transpose matrix 
205		// according to row-col value 
206		return result; 
207	} 
208
209	void multiply(sparse_matrix b) 
210	{ 
211		if (col != b.row) 
212		{ 
213
214			// Invalid multiplication 
215			cout << "Can't multiply, Invalid dimensions"; 
216			return; 
217		} 
218
219		// transpose b to compare row 
220		// and col values and to add them at the end 
221		b = b.transpose(); 
222		int apos, bpos; 
223
224		// result matrix of dimension row X b.col 
225		// however b has been transposed, 
226		// hence row X b.row 
227		sparse_matrix result(row, b.row); 
228
229		// iterate over all elements of A 
230		for (apos = 0; apos < len;) 
231		{ 
232
233			// current row of result matrix 
234			int r = data[apos][0]; 
235
236			// iterate over all elements of B 
237			for (bpos = 0; bpos < b.len;) 
238			{ 
239
240				// current column of result matrix 
241				// data[,0] used as b is transposed 
242				int c = b.data[bpos][0]; 
243
244				// temporary pointers created to add all 
245				// multiplied values to obtain current 
246				// element of result matrix 
247				int tempa = apos; 
248				int tempb = bpos; 
249
250				int sum = 0; 
251
252				// iterate over all elements with 
253				// same row and col value 
254				// to calculate result[r] 
255				while (tempa < len && data[tempa][0] == r && 
256					tempb < b.len && b.data[tempb][0] == c) 
257				{ 
258					if (data[tempa][1] < b.data[tempb][1]) 
259
260						// skip a 
261						tempa++; 
262
263					else if (data[tempa][1] > b.data[tempb][1]) 
264
265						// skip b 
266						tempb++; 
267					else
268
269						// same col, so multiply and increment 
270						sum += data[tempa++][2] * 
271							b.data[tempb++][2]; 
272				} 
273
274				// insert sum obtained in result[r] 
275				// if its not equal to 0 
276				if (sum != 0) 
277					result.insert(r, c, sum); 
278
279				while (bpos < b.len && 
280					b.data[bpos][0] == c) 
281
282					// jump to next column 
283					bpos++; 
284			} 
285			while (apos < len && data[apos][0] == r) 
286
287				// jump to next row 
288				apos++; 
289		} 
290		result.print(); 
291	} 
292
293	// printing matrix 
294	void print() 
295	{ 
296		cout << "\nDimension: " << row << "x" << col; 
297		cout << "\nSparse Matrix: \nRow\tColumn\tValue\n"; 
298
299		for (int i = 0; i < len; i++) 
300		{ 
301			cout << data[i][0] << "\t " << data[i][1] 
302				<< "\t " << data[i][2] << endl; 
303		} 
304	} 
305}; 
306
307// Driver Code 
308int main() 
309{ 
310
311	// create two sparse matrices and insert values 
312	sparse_matrix a(4, 4); 
313	sparse_matrix b(4, 4); 
314
315	a.insert(1, 2, 10); 
316	a.insert(1, 4, 12); 
317	a.insert(3, 3, 5); 
318	a.insert(4, 1, 15); 
319	a.insert(4, 2, 12); 
320	b.insert(1, 3, 8); 
321	b.insert(2, 4, 23); 
322	b.insert(3, 3, 9); 
323	b.insert(4, 1, 20); 
324	b.insert(4, 2, 25); 
325
326	// Output result 
327	cout << "Addition: "; 
328	a.add(b); 
329	cout << "\nMultiplication: "; 
330	a.multiply(b); 
331	cout << "\nTranspose: "; 
332	sparse_matrix atranspose = a.transpose(); 
333	atranspose.print(); 
334} 
335
336// This code is contributed 
337// by Bharath Vignesh J K 

خلاصه و جمع‌بندی

در این نوشتار با نحوه تعریف و کاربرد ماتریس خلوت در ریاضیات و ساختمان داده آشنا شدیم. همچنین شیوه‌های مختلف ذخیره سازی این ماتریس نیز بازگو و نحوه پیاده‌سازی آن در زبان برنامه‌نویسی ++C مورد بررسی قرار گرفت. از آنجایی که این ساختارها با حجم بسیار کمتری از حافظه، ماتریس‌های خلوت را ذخیره می‌کنند، کاربردهای زیادی در حل دستگاه معادلات یا معادلات دیفرانسیل روی رایانه‌ها دارند.