تابع متناوب و خصوصیات آن | به زبان ساده
یکی از توابع ریاضی که البته در فیزیک، بخصوص توصیف پدیدههای تکراری، نقش مهمی دارد، تابع متناوب (Periodic Function) است. توابع مثلثاتی و همچنین توابعی که با زاویه یا موج سرو کار دارند، اغلب از نوع توابع متناوب محسوب میشوند. با توجه به اهمیت این توابع در پدیدههای فیزیکی و طبیعی، این نوشتار از مجله فرادرس را به معرفی تابع متناوب و خصوصیات آن اختصاص دادهایم.
برای آشنایی بیشتر با مفهوم تابع و ویژگیهای اصلی آن بهتر است نوشتار رابطه و تابع از نگاه مجموعه ها — به زبان ساده و ضرب دکارتی مجموعه ها و مختصات دکارتی — به زبان ساده را مطالعه کنید. همچنین خواندن مطالب مجموعه ها در ریاضیات – مفاهیم پایه و اعداد مختلط — به زبان ساده نیز خالی از لطف نیست.
تابع متناوب و خصوصیات آن
از نقطه نظر ریاضی، به طور کلی تابعی که مقدارش را در بازههای مشخصی تکرار کند، یک تابع متناوب یا تناوبی (Periodic Function) نامیده میشود. برای مثال «تابع سینوس» (Sine Function) به عنوان یک «تابع مثلثاتی» (Triangle Function) دارای دوره تناوب $$2 \pi $$ رادیان است. چنین توابعی در پدیدههای مرتبط با موج و نوسان که به صورت حرکت رفت و برگشت هستند، کاربرد دارند.
نکته: توابعی که تناوبی نباشند، به توابع «غیرتناوبی» (Aperiodic) مشهورند.
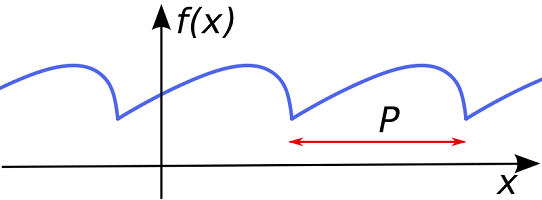
به تصویر ۱، توجه کنید. تابع $$f(x)$$ یک تابع متناوب است که طول دوره تناوب در آن نیز برابر با $$P$$ است. واضح است که مقدار تابع در نقطه $$x$$ و $$x+P$$ برابر است. همین موضوع میتواند مبنایی برای تعریف تابع متناوب باشد.
تعریف تابع متناوب
تابع $$f$$ با دامنه $$D_f$$، یک تابع متناوب (Periodic Function) است، اگر برای مقدار غیر صفر $$P$$، داشته باشیم:
$$ \large f (x + P) = f(x), \; \; P \neq 0 , \;\;\; \forall x , x \pm P \in D_f $$
در این حالت واضح است که $$x$$ و $$x+P$$ باید در دامنه تابع $$f$$ باشند. در ضمن مقدار $$P$$ را میزان یا «دوره تناوب» (Period) تابع $$f$$ مینامند. در حالتی که $$P$$، کوچکترین مقدار مثبتی باشد که در آن تابع $$f$$ دارای تناوب میشود، $$P$$ را «تناوب پایه» (Fundamental Period)، یا «تناوب اصلی» (Primitive Period) میگویند.
نکته: اغلب، مقدار $$P$$ را همان تناوب اصلی در نظر میگیرند. مقدار تابع متناوب با دوره تناوب $$P$$، در فاصلههایی با طول $$P$$، تکرار میشود. گاهی این فاصلهها را تناوبهای تابع $$f$$ مینامند.
از لحاظ هندسی، تابع متناوب، دارای خاصیت «تقارن انتقالی» (Translational symmetry) است. به این معنی که اگر هر نقطه از یک فاصله تناوبی را روی نقطه متناظرش قرار دهیم، شکل یا منحنیها بر یکدیگر منطبق شده و الگوی یکسانی حاصل میشود. در نتیجه تابع متناوب در طول یا فاصلههای متناوبش، یکسان بوده و دارای تقارن است. به بیان دیگر میتوان تابع $$f$$ را متناوب با دوره تناوب $$P$$ دانست، اگر نمودار تابع $$f$$، در مقادیر مختلف روی محور افقی با فاصله $$P$$، یکسان باشد. این خاصیت را «ناوردایی» (Invariant) نسبت به جابجایی با طول $$P$$ میگویند.
آشنایی با چند تابع متناوب حقیقی
در این بخش به معرفی چند تابع میپردازیم که در «مجموعه اعداد حقیقی» (Real Numbers Set)، متناوب هستند.
تابع سینوس
همانطور که گفته شد، توابع مثلثاتی، در گروه توابع متناوب طبقهبندی میشوند. در اینجا به بررسی «تابع سینوس» (Sine Function) و خصوصیات تناوبی آن میپردازیم. البته دیگر توابع مثلثاتی نیز همین خصوصیات را خواهند داشت.
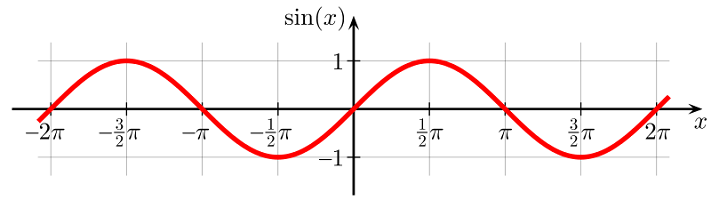
به تصویر ۲ دقت کنید. نمودار تابع سینوس روی محورهای «مختصات دکارتی» (Cartesian Coordinates) ترسیم شده است. واضح است که مقدار تابع با دوره تناوب $$2\pi$$ تکراری است. با توجه به تعریف تابع متناوب و سینوس، مشخص است که میتوان فرمول زیر را برای این تابع نوشت.
$$ \large \sin (x + 2 \pi) = \sin ( x ) , \; \; \forall x \in {\cal{R}} $$
تابع کسینوس
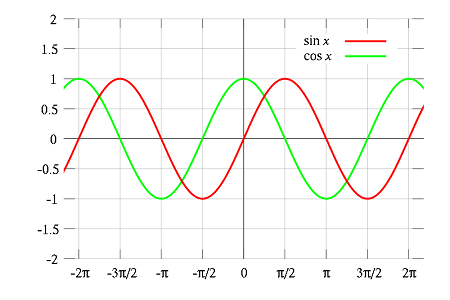
واضح است که تابع کسینوس (Cosine) نیز تابعی متناوب است. دوره تناوب برای چنین تابعی نیز $$P = 2 \pi$$ است. در تصویر ۳، مقایسهای بین دو تابع سینوس و کسینوس صورت گرفته و مشخص است که هر دو دارای دوره تناوب $$2\pi$$ هستند. ولی با توجه به تغییر فاز در آنها، تابع سینوس و کسینوس بر یکدیگر منطبق نیستند.
ایده اصلی در «سری فوریه» (Fourier Series) نیز براساس توابع مثلثاتی است و مشخص میکند که بیان هر تابع تناوبی به کمک مجموع چندین تابع سینوسی (یا توابع مثلثاتی دیگر) میسر است.
تابع جزء اعشاری
«تابع جزء اعشاری» (Fractional Part)، قسمت اعشار (برای مقادیر مثبت) هر عدد را نشان میدهد. این تابع را با نماد $$P_x$$ نشان داده و بر پایه تابع «جزء صحیح» (Integer Function) معرفی و به صورت زیر تعریف میشود.
$$ \large P_x = x - [x] ,\;\; x \in {\cal{R}} $$
واضح است به علت رابطه زیر، دامنه این تابع اعداد حقیقی و برد آن بازه $$[0,1)$$ است.
$$ \large [x] \leq x < [x] + 1 $$
به علامت کوچکتر یا مساوی در سمت چپ رابطه بالا دقت کنید. برای مثال تابع جزء اعشاری را برای مقادیر 0.5 , 1.5 , 2.5 محاسبه کردهایم. جالب است که همگی آنها مقداری برابر و ثابت دارند. این امر نشانگر آن است که تابع جزء اعشاری دارای دوره تناوب بوده و یک تابع متناوب محسوب میشود.
$$ \large {\displaystyle P_{(0.5)} = P_{(1.5)} = P_{(2.5)} = \cdots = 0.5} $$
همانطور که مشخص است، طول فاصله یا دوره تناوب چنین تابعی، برابر با واحد (۱) است. نمودار این تابع را در تصویر ۴ مشاهده میکنید. شکل این تابع به صورت «امواج دندان ارهای» (Sawtooth Wave) است.
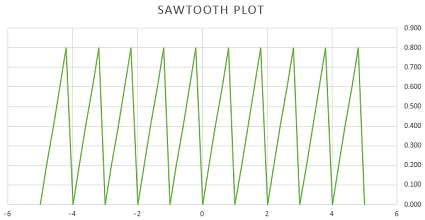
تابع دریکله
فرض کنید تابع $$f$$ به صورت زیر روی اعداد حقیقی $${\cal{R}}$$ و البته گویا $${\cal{Q}}$$ تعریف شده باشد.
$$ \large {\displaystyle f(x) = {\begin{cases}1 , & x \in \mathbb {Q} ,\\ 0 , & x \in (\mathbb {R} - \mathbb {Q} ) \end{cases}}}$$
واضح است که دامنه این تابع اعداد حقیقی و همدامنه یا برد آن دو عدد صحیح ۰ و ۱ است.
$$ \large {\displaystyle f \colon \mathbb {R} \mapsto \{0,1\}} $$
به این ترتیب اگر $$x$$، عدد گویا باشد، مقدار تابع برابر با ۱ و در غیر اینصورت (عدد $$x$$، گنگ باشد) صفر خواهد بود. چنین تابعی به نام «تابع دریکله» (Dirichlet function) معروف است. حتی میتوان چنین تابعی را به عنوان تابع نشانگر اعداد گویا نیز به شمار آورد.
مشخص است که این تابع در اعداد حقیقی، پیوسته نبوده و انتگرالپذیر نیز نیست. این تابع به علت کاوشهای «پیتر دریکله» ( Peter Gustav Lejeune Dirichlet)، ریاضیدان آلمانی، به نام تابع دریکله خوانده میشود.
هر چند نمیتوان این تابع را رسم کرد ولی واضح است که با توجه به نحوه تعریف آن، تابع دریکله یک تابع متناوب در نظر گرفته میشود که طول یا مقدار دوره تناوب آن اعداد گویا غیر صفر است.
فرمول اویلر یا تابع متناوب مختلط
در این قسمت، توابع متناوبی را معرفی میکنیم که ضرایب آن «اعداد مختلط» (Complex Number) هستند. برای مثال به تابع نمایی مختلط زیر توجه کنید.
$$ \large {\displaystyle e^{ i \ k \ x} = \cos k \ x + i \, \sin k \ x } $$
از آنجایی که دو تابع سینوس و کسینوس، متناوب با دوره تناوب $$2 \pi$$ هستند، تابع نمایی مختلط نیز یک تابع متناوب با شکل موجهای سینوسی و کسینوسی است.
این امر به این معنی است که «فرمول اویلر» (Euler's Formula) که در رابطه بالا معرفی شد، متناوب با طول یا دوره تناوب $$L$$ بوده که به صورت زیر محاسبه میشود.
$$ \large {\displaystyle L = {\frac {2 \pi }{k}}} $$
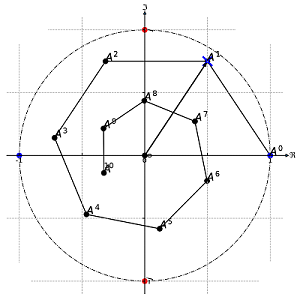
توابع مختلط، ممکن است در طول یک محور در صفحه مختلط، تناوبی باشند اما در محور دیگر چنین امری محقق نشود. به عنوان مثال تابع نمایی زیر روی «محور موهومی» (Imaginary Axis)، متناوب بوده ولی روی «محور حقیقی» (Real Axis)، تناوب ندارد. چنین وضعیتی را در نمودار مشخص شده در تصویر ۵، مشاهده میکنید که در آن تابع زیر رسم شده است. البته نقاط مورد محاسبه، مقادیر صحیح هستند. به همین دلیل نمودار به صورت شکسته ترسیم شده است.
$$ \large {\displaystyle e ^ {z}} = \exp(z) ,\;\;\;z \in {\cal{C}}$$
نکته: تابعی که دامنه آن اعداد مختلط باشند، میتواند دارای دو دوره «تناوب ناسازگار» (Incommensurate Period) باشد که البته ثابت نیستند. «توابع بیضوی» (Elliptic Functions) از این گونه توابع محسوب میشوند.
تابع متناوب در زندگی
تابع متناوب در زندگی روزمره نیز نمود پیدا میکند. هر گاه پدیدهای وابسته به زمان و تکرار پذیر باشد، تغییرات آن توسط یک تابع متناوب قابل بیان است. برای مثال حرکت چرخشی عقربههای ساعت، حرکت نوسانی یک آونگ و حرکت ماه و خورشید در آسمان، نمونههایی از پدیدههای واقعی محسوب میشوند که دارای «حرکت متناوب» (Periodic Motion) هستند. حرکت متناوب، تغییر موقعیت یک سیستم است که توسط یک تابع متناوب قابل توصیف بوده و در دوره تناوب به طور یکسان تکرار میگردد.
در این حالت، توابع با دامنه «اعداد حقیقی» (Real Numbers) یا «اعداد صحیح» (Integer Numbers) را میتوان در یک مختصات دکارتی ترسیم کرد و تکرار منحنی حاصل را در فواصلی با دوره تناوب $$P$$ مشاهده کرد.
خواص تابع متناوب
یکی از ویژگیهای جالب برای توابع تناوبی در مقادیر آن نهفته است. نتیجه محاسبه تابع متناوب شامل مقدار تکراری است. بخصوص اگر دوره تناوب تابع متناوب $$f$$ برابر با $$P$$ باشد، برای هر مقدار $$x$$ در دامنه تابع $$f$$ و مقدار صحیح مثبت $$n$$، رابطه زیر برقرار است.
$$ \large {\displaystyle f ( x + n P)= f ( x )} $$
از طرفی اگر $$a$$ یک عدد حقیقی غیر صفر باشد و $$ax$$ نیز در دامنه تابع متناوب $$f$$ قرار گیرد، آنگاه با فرض آنکه $$P$$ دوره تناوب تابع $$f$$ باشد، دوره تناوب تابع $$f(a x )$$ برابر است با $$\frac{P}{|a|}$$. برای مثال اگر $$f( x ) = \sin(x)$$ باشد، میدانیم $$P = 2 \pi$$. در نتیجه دوره تناوب تابع $$\sin( 5 x ) $$ نیز برابر است با $$\frac{ 2 \pi }{5}$$.
سری فوریه و تابع متناوب
بعضی از توابع متناوب را میتوان با سری فوریه (Fourier Series) شرح داد. به عنوان مثال، برای توابع $$L^2$$، «قضیه کارلسون» (Carleson's Theorem)، بیان میکند که چنین توابعی، «تقریباً همه جا» (Almost Everywhere) به یک سری فوریه، به صورت نقطهای (Lebesgue) همگرا هستند.
سری فوریه فقط برای توابع متناوب یا توابع در فاصله کراندار قابل استفاده است. اگر $$ {\displaystyle f} $$ یک تابع متناوب با دوره $$ {\displaystyle P} $$ بوده و بتوان آن را به صورت یک سری فوریه نوشت، آنگاه، ضرایب این سری را میتوان با انتگرال روی فاصله تناوب $$ { \displaystyle P} $$ مشخص کرد.
محاسبه دوره تناوب
یک موج صوتی حاصل از نتهای موسیقی متشکل از فرکانسهای ترکیبی مختلف را در نظر بگیرید، این موج به وسیله فرکانسهای پایهای از نسبتهای زیر تشکیل شده است.
$$ \large f: F = \frac{1}{f} [f_1\; f_2\; f_3\; \cdots \; f_N ] $$
که در آن، همه عناصر غیر صفر بزرگتر یا مساوی با ۱ هستند و برای حداقل یک مورد تساوی با ۱ برقرار است.
به منظور محاسبه دوره تناوب $$T$$، ابتدا «کوچکترین مخرج مشترک» (Least Common Denominator) یا LCD بین عوامل $$f_1,\; \cdots \; ,f_N$$ را پیدا میکنیم. به این ترتیب میتوان دوره تناوب را به صورت زیر در نظر گرفت.
$$ \large T = \dfrac{ \text{LCD}}{f} $$
در حالتی که رابطه به صورت سینوسی باشد، دوره تناوب $$T = \dfrac{1}{f}$$ خواهد بود. به این ترتیب LCD را میتوان به صورت مضرب تناوب در نظر گرفت.
- «نتهای گام ماژور موسیقی کلاسیک غربی» (Notes of Western Major scale) را در نظر گیرید. در اینجا برای مشخص کردن نُتها این گام، از تناوبهای فرکانسی که دارای نظمی به صورت $$ [1,\; 9⁄8.\; 5⁄4,\; 4⁄3,\; 3⁄2,\; 5⁄3,\; 15⁄8] $$ هستند، استفاده میکنیم. در نتیجه LCD برابر با ۲۴ بوده و دوره تناوب برابر است با $$T = \dfrac{24}{f}$$.
- برای نمایش مجموعه همه «نتهای آکورد ماژور سه نتی» (Notes of a major triad) خواهیم داشت: $$[1,\; 5⁄4,\; 3⁄2]$$. پس کوچکترین مخرج مشترک برابر با ۱۰ بوده و $$T = \frac{10}{f}$$ خواهد بود.
- همچنین برای نمایش «نتهای آکورد مینور سه نتی» (Notes of a minor triad) نیز از ترتیب $$[1,\; 6⁄5,\; 3⁄2]$$ استفاده خواهیم کرد. پس LCD = 10، در نتیجه $$T = \dfrac{10}{f} $$
نکته: اگر حداقل مخرج مشترک (LCD) وجود نداشته باشد، یعنی مثلا یکی از عناصر فوق گویا نباشند، موج به صورت متناوب نخواهد بود.
تابع متناوب تعمیم یافته
در این بخش، با تعمیم مفهوم تناوب و تابع تناوبی آشنا خواهیم شد. در این بین دو نوع تابع جدید نیز معرفی شده که با تابع متناوب در ارتباط هستند.
توابع ضد تناوبی
یکی از زیر مجموعههای متداول توابع تناوبی، تابع «ضد تناوبی» (Antiperiodic Function) یا تناوبی قرینه است. این تابع به گونهای است که پس از طی شدن یک دوره تناوب، تابع با قرینه مقدار قبل از تناوب برابر میشود.
$$ \large {\displaystyle f (x + P) = − f (x), \;\; \forall x , x + P \in D_f } $$
همانطور که مشخص است تابع ضد تناوبی با دوره «ضد تناوب $$P$$» (P-antiperiodic) یک تابع با دوره تناوب $$-2P$$ است. به عنوان مثال، توابع سینوس و کسینوس تابع ضد تناوبی با دوره ضد تناوبی $$\pi$$ و دوره تناوب $$2 \pi$$ هستند.
نکته: توابع ضد تناوبی با دوره تناوبی $$P$$، یک تابع متناوب با دوره تناوب $$2 P$$ هستند ولی عکس این موضوع لزوما صحیح نیست.
تابع متناوب بلاک
یک تعمیم دیگر روی توابع متناوب، در حوزه «امواج بلاک» (Bloch Waves) و نظریه Floquet است که وضعیت پاسخهای «معادلات دیفرانسیل متناوب» (Periodic Differential Equations) را مشخص میکند. در این زمینه، راه حل یا پاسخها (در حالت تک متغیره و تک بُعد) به فرم تابع زیر هستند:
$$ \large { \displaystyle f (x + P) = e ^ { i \ \; k \;P} f (x) } $$
بطوری که $$k$$، یک عدد حقیقی یا مختلط است.
توابعی به این شکل را به نام «توابع متناوب بلاک» (Bloch-periodic functions) میشناسند. یک تابع متناوب در این حالت با $$k=0$$ مشخص شده و تابع ضد تناوبی نیز حالت خاصی از تابع متناوب بلاک با $$k = \frac{\pi}{P}$$ است.
فضاهای مهم به عنوان دامنه
در مبحث مربوط به «پردازش سیگنال» (Signal Processing) با مسائلی روبرو میشوید که نیاز به استفاده از سریهای فوریه دارند. اما ممکن است توابع متناوب را نتوانید با سری فوریه حل کرد، زیرا انتگرالهای مورد نیاز برای سری فوریه در این حالت در بعضی از وضعیتها، همگرا نیستند. راه ممکن، به کارگیری یک دامنه محدود برای تعریف تابع متناوب است. برای این منظور میتوانید از مفهوم «فضای بخشی» (Quotient Space) استفاده کنید:
$$ \large {\mathbb{R} / \mathbb{Z}}
= \{x + \mathbb{Z} : x \in \mathbb{R}\}
= \{\{y : y\in\mathbb{R}\land y - x \in\mathbb{Z} \} : x \in \mathbb{R} \}$$
رابطه بالا به این معنی است که هر عنصر در $$ {\displaystyle {\mathbb {R} / \mathbb {Z}}} $$ در یک کلاس هم ارزی اعداد حقیقی قرار گرفته که دارای «جزء کسری» (Fractional Part) مشابه است. بنابراین تابعی مانند $$ {\displaystyle f: {\mathbb {R} / \mathbb {Z}} \to \mathbb Z } $$ به عنوان یک تابع متناوب با دوره تناوب 1 در نظر گرفته میشود.
معرفی چند تابع متناوب پر کاربرد
در جدولهای زیر توابع متناوب پر کاربرد در حوزههای مختلف علمی، معرفی شدهاند. البته آنها را به دو دسته، «توابع مثلثاتی» (Trigonometric Functions) و «توابع ناهموار» (Non-smooth Functions) طبقهبندی کردهایم.
توابع مثلثاتی
توابع مثلثاتی که در جدول ۱ دیده میشوند، متناوب بوده و دوره تناوب آنها $$2 \pi$$ است. البته در مواردی که دوره تناوب متفاوت است، در جدول دوره تناوب مشخص شده. توجه داشته باشید که $$U_n$$، تابع $$n$$امین عدد بالا یا پایین (Up/down Number) است. همچنین $$B_n$$ نیز بیانگر $$n$$امین «عدد برنولی» (Bernoulli Number) است.
جدول ۱: توابع مثلثاتی (متناوب) به همراه سری فوریه آنها
| نام تابع | نماد تابع | فرمول | سری فوریه |
| سینوس - Sine | $$ \large {\displaystyle \sin(x)} $$ | $$ \large {\displaystyle \sum_{n = 0}^{\infty }{\frac {(- 1 )^{n} x^{ 2 n + 1}}{(2 n + 1)!}}} $$ | $$ \large {\displaystyle \sin(x)} $$ |
| cas | $$ \large {\displaystyle \operatorname {cas} (x)} $$ | $$ \large {\displaystyle \sin(x) + \cos(x)} $$ | $$ \large {\displaystyle \sin(x) + \cos(x)} $$ |
| کسینوس - Cosine | $$ \large {\displaystyle \cos(x)} $$ | $$ \large {\displaystyle \sum_{n = 0}^{\infty }{\frac {(-1)^{n} x^{ 2 n }}{(2n)!}}} $$ | $$ \large {\displaystyle \cos(x)} $$ |
| cis | $$ \large {\displaystyle e^{ix},\operatorname {cis} (x)} $$ | $$ \large {\displaystyle \cos(x) + i\sin(x) }$$ | $$ \large {\displaystyle \cos(x) + i \sin(x)} $$ |
| تانژانت - Tangent | $$ \large {\displaystyle \tan(x)} $$ | $$ \large {\displaystyle \sum_{n = 0}^{\infty }{\frac {U_{2 n + 1 }x^{2 n + 1 }}{(2 n + 1)!}}} $$ | $$ \large {\displaystyle 2\sum _{n = 1}^{\infty }( - 1)^{n - 1}\sin(2nx)} $$ |
| کتانژانت - Cotangent | $$ \large {\displaystyle \cot(x)} $$ | $$ \large {\displaystyle \sum_{n = 0}^{\infty }{\frac {( - 1 )^{n}2^{2 n} B_{2 n}x^{2 n - 1}}{(2 n)!}}} $$ | $$ \large {\displaystyle i + 2 i \sum_{n = 1}^{\infty }(\cos 2 n x - i \sin 2 n x)}$$ |
| سکانت - Secant | $$ \large {\displaystyle \sec(x)}$$ | $$ \large {\displaystyle \sum_{n = 0}^{\infty }{\frac {U_{2n}x^{2n}}{(2 n )!}}} $$ | |
| کسکانت - Cosecant | $$ \large {\displaystyle \csc(x)} $$ | $$ \large {\displaystyle \sum _{n = 0}^{\infty }{\frac {(-1)^{ n + 1 }2 \left(2^{2 n - 1 } - 1 \right) B_{ 2 n }x^{ 2 n - 1 }}{(2n)!}}} $$ |
چند تابع متناوب ناهموار
در جدول ۲، بعضی از توابع متناوب که رفتار همواری نداشته و در همه نقاط دامنه خود، مشتقپذیر نیستند، دیده میشوند.
توابع این جدول، با متغیر $$x$$ مشخص شده و $$p$$ نیز دوره تناوب بوده که در بازه $$[-1,1]$$ تغییر میکند. نماد $${\displaystyle \lfloor n\rfloor }$$ نیز جزء صحیح یا تابع کف بوده و همچنین $$\text{sgn}$$ هم «تابع علامت» (Sign Function) است.
جدول ۲: توابع متناوب ناهموار
| نام تابع | فرمول محاسباتی | سری فوریه | توضیحات |
| تابع مثلثی - Triangle Wave | $$ \large {\displaystyle {\frac {4}{p}} \left(x -{\frac {p}{2}}\left\lfloor {\frac {2 x}{p}} + {\frac {1}{2}}\right\rfloor \right)(- 1)^{\left\lfloor {\frac {2 x}{p}} + {\frac {1}{2}}\right\rfloor }}$$ | $$ \large {\displaystyle {\frac {8}{\pi ^{2}}}\sum _{n\,\mathrm {odd} }^{\infty }{\frac {(-1)^{n - 1}}{n^{2}}}\sin \left({\frac {2\pi nx}{p}}\right)} $$ | |
| تابع دندان ارهای - Sawtooth Wave | $$ \large {\displaystyle 2 \left({\frac {x}{p}}-\left\lfloor{\frac {1}{2} } + {\frac {x}{p}}\right\rfloor \right)} $$ | $$ \large {\displaystyle {\frac {2}{\pi }}\sum _{n = 1}^{\infty }{\frac {(-1)^{n-1}}{n}}\sin \left({\frac {2n\pi x}{p}}\right)} $$ | |
| تابع موج مربعی - Square Wave | $$ \large {\displaystyle \operatorname {sgn} \left(\sin {\frac {2 \pi x}{p}} \right)} $$ | $$ \large {\displaystyle {\frac {4}{\pi }}\sum _{n\,\mathrm {odd} }^{\infty }{\frac {1}{n}}\sin \left({\frac {2n\pi x}{p}}\right)} $$ | |
| Cycloid |
$$ \large {\displaystyle {\frac {p(1-\cos(f^{(-1)}{\Bigl(}{\frac {2\pi x}{p}}{\Bigr)}))}{2\pi }}} $$ | - |
$$ \large {\displaystyle f(x) = x - \sin(x)} $$ $$ \large {\displaystyle f^{(-1)}(x)}$$ معکوس حقیقی تابع $$f$$است. |
| تابع موج پالس - Pulse Wave | $$ \large {\displaystyle H(\cos {\Bigl(}{\frac {2\pi x}{p}}{\Bigr)} - \cos {\Bigl(}{\frac {\pi t}{p}}{\Bigr)})} $$ | $$ \large {\displaystyle {\frac {t}{p}} + \sum _{n = 1}^{\infty }{\frac {2}{n\pi }}\sin \left({\frac {\pi nt}{p}}\right)\cos \left({\frac {2\pi nx}{p}}\right)} $$ | $$H$$ تابع پلهای هویساید و $$t$$ زمان پالس است. |
خلاصه و جمعبندی
همانطور که دیدید، تابع متناوب و خصوصیات آن در بسیاری از شاخههای دیگر علوم به کار گرفته شده و قادر به توصیف تغییر پذیری پدیدههای فیزیکی و شیمیایی هستند. توابع مثلثاتی و بعضی از توابع پلهای از جمله توابع متناوب هستند. در این متن همچنین در مورد دوره تناوب برای تابع متناوب صحبت کرده و نحوه محاسبه آن را مورد بررسی قرار دادیم. در انتها نیز با توابع متناوب مختلط آشنا شده و تعمیم تابع متناوب را در حالتهای مختلف بازگو کردیم.











می شه توی یه آموزش اثبات اینکه چرا دوره تناوب توابع متناوب سینوسی وقتی بهشون یه ثابت اضافه می شه دوبرابر می شه رو توضیح بدید