تابع بیشینه هموار (Softmax) چیست؟ | به زبان ساده

بحث نرمال‌سازی یا استاندارد سازی داده‌ها، برای مقایسه و به کارگیری روش‌های آماری چند متغیره، مانند «خوشه‌بندی» (Clustering) و «رده‌بندی» (Classification) اهمیت زیادی دارد. توابع و روش‌های مختلفی برای انجام این کار وجود دارد. در این نوشتار به تابع بیشینه هموار (softmax) خواهیم پرداخت و خصوصیات آن را مورد بررسی قرار می‌دهیم.

به منظور آشنایی بیشتر با مفهوم استاندارد یا نرمال سازی بهتر است مطالب دیگر مجله فرادرس مانند توزیع بولتزمان در ترمودینامیک آماری— به زبان ساده و روش‌های استاندارد سازی داده‌ها را مطالعه کنید. همچنین خواندن مطالب انحراف استاندارد و خطای استاندارد — از صفر تا صد و متغیر تصادفی، تابع احتمال و تابع توزیع احتمال نیز خالی از لطف نیست.

تابع بیشینه هموار

تابع بیشینه هموار (Softmax Fucntion)، همچنین به عنوان softargmax یا «تابع نمایی نرمال شده» (normalized exponential function)، شناخته می‌شود. از طرفی این تابع را تعمیم‌یافته «تابع لجستیک» (Logistic Function) در حالت چند بُعدی محسوب می‌کنند. همچنین از آن در «رگرسیون لجستیک چند جمله‌ای» (Multinomial Logistic Regression) استفاده می‌شود و غالباً به عنوان آخرین «تابع فعال‌سازی» (Activation Function) برای یک «شبکه عصبی» (Neural Network) برای نرمال سازی خروجی شبکه و تبدیل آن به توزیع احتمال بهره می‌برند. نرمال سازی در این حالت نسبت به کلاس‌های خروجی پیش بینی شده، صورت می‌گیرد.

فیلم مجموعه آموزش داده کاوی و یادگیری ماشین – مقدماتی تا پیشرفته در فرادرس

کلیک کنید

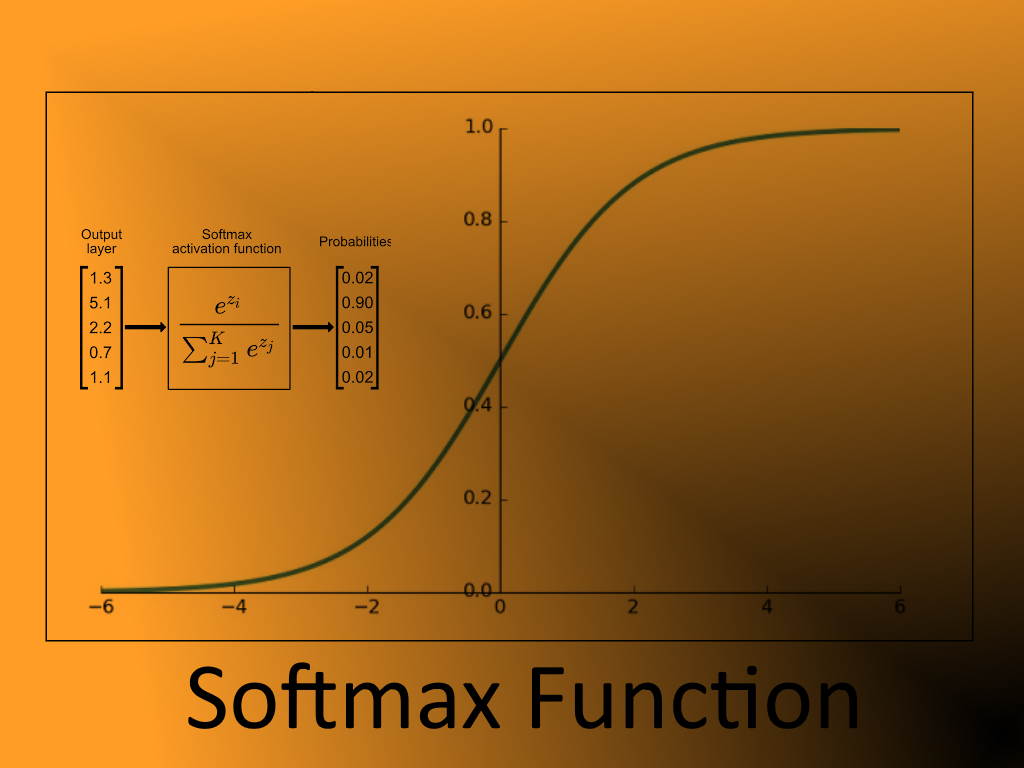
تابع بیشینه هموار، به عنوان ورودی یک بردار $$z$$ از $$k$$ عدد حقیقی را می‌گیرد و آن را به یک توزیع احتمال تبدیل می‌کند که متشکل از $$k$$ احتمال متناسب با نمای اعداد ورودی هستند. این امر به این معنی است که قبل از استفاده از تابع بیشینه هموار (Softmax)، بعضی از اجزای بردار $$z$$ ممکن است منفی یا بیشتر از یک باشند. اما بعد از استفاده از تابع بیشینه هموار، هر مولفه در بازه $${\displaystyle (0،1)}$$ قرار می‌گیرد بطوری که مجموع آن‌ها برابر با ۱ باشد. بنابراین می‌توان آنها را به عنوان مقدار احتمال تفسیر کرد. علاوه بر این، ورودی‌های با مقادیر بزرگتر، دارای احتمال بیشتر نیز خواهند بود.

تابع استاندارد بیشینه هموار که گاهی به آن «تابع بیشینه هموار واحد» (Unit Softmax Function) نیز گفته می‌شود، به صورت زیر تعریف می‌شود.

$$\large {\displaystyle \sigma (\mathbf {z}_{i}) = {\dfrac {e ^ {z_{i}}} {\sum_ {j = 1} ^ {k} e ^ {z_ {j} }}} {\text { for }} i = 1, \dotsc, k {\text { and }} \mathbf {z} = (z_{1}, \dots, z_{k}) \in \mathbb { R} ^ {k}}$$

رابطه ۱

توجه داشته باشید که در $${\displaystyle \sigma: \mathbb {R} ^ {K} \to \mathbb {R} ^ {k}}$$ تعریف شده است.

توجه داشته باشید که برای هر عنصر $${\displaystyle z_ {i}}$$ از بردار ورودی $${\displaystyle \mathbf {z}}$$، تابع نمایی استاندارد اعمال شده است و تقسیم کردن هر مقدار بر مجموع تمامی آن‌ها، باعث نرمال شدن شده و اطمینان می‌دهد که مجموع اجزای بردار خروجی یک خواهد بود.

$$\large {\displaystyle \sigma (\mathbf {z}) = 1 }$$

البته به جای استفاده از عدد نیر ($$e$$) به عنوان پایه تابع نمایی، می‌توان از یک پایه متفاوت مثل $$b > 0$$ نیز استفاده کرد. انتخاب مقدار بزرگ برای $$b$$ باعث می‌شود که توزیع احتمالی، چگالی مقادیر خروجی، حول مقادیر بزرگتر، بیشتر شود. به این ترتیب برای مقدار حقیقی $$\beta$$، به صورت $${\displaystyle b = e ^ {\beta}}$$ یا $${\displaystyle b = e ^ {- \beta}}$$ خواهیم داشت:

$$\large \displaystyle \sigma (\mathbf {z}_{i}) = {\dfrac {e ^ {\beta z_{i}}} {\sum_ {j = 1} ^ {k} e ^ {\beta z_{j}}}}$$

رابطه ۲

یا

$$\large {\displaystyle \sigma (\mathbf {z}_ i}) = {\dfrac {e ^ {- \beta z_ {i}}} {\sum_ {j = 1} ^ {k} e ^ {- \beta z_ {j}}}}$$

رابطه ۳

رابطه‌های بالا (رابطه ۲ و ۳) به ازای $$i = 1 , \ldots ,k$$ برقرار خواهند بود. در بعضی از زمینه‌ها یا حوزه‌های علوم، پایه برای تابع بیشینه هموار، ثابت در نظر گرفته می‌شود ولی گاهی اوقات نیز پارامترها $$\beta$$ تغییرپذیر خواهند بود.

تاریخچه تابع بیشینه هموار

از تابع بیشینه هموار، در «مکانیک آماری» (Statistical Mechanic) در «توزیع بولتزمان» (Boltzmman Distribution) که در مقاله بنیادی او در سال 1868 منتشر شد، استفاده شده است. همچنین در کتاب معروف و تاثیر گذار «گیبس» (Gibbs) در سال ۱۹۰۸ نیز تابع بیشینه هموار به کار رفته و برای حل مسائل مرتبط با سیستم‌های مبتنی بر مکانیک آماری و ترمودینامیک آماری، امری ضروری تلقی شده‌اند.

استفاده از تابع بیشینه هموار در «نظریه تصمیم» (Decision Theory)  نیز استفاده می‌شود. کارهایی که «دنکان لوسه» (Duncan Luce) در سال ۱۹۵9 انجام داد، باعث استفاده از شرط استقلال در «نظریه انتخاب منطقی» (Rational Choice Theory) شد. او در این زمینه از تابع بیشینه هموار برای ترجیح نسبی استفاده کرد.

در سال ۱۹۹۰ «جان بریدل» (John Bridle) برای الگوریتم‌های یادگیری ماشین، از تابع بیشینه هموار بهره گرفت و نشان داد که برای شبکه‌های عصبی غیر خطی یا پرسپترون‌های چند لایه (MLP)، استفاده از تابع بیشینه هموار، می‌تواند نتیجه بسیار بهتری ارائه کند. او این موضوع را به صورت زیر بیان کرد.

ما در حوزه شبکه‌های غیر خطی پیشخور (پرسپترون چند لایه یا MLP) با چندین خروجی مواجه هستیم و می‌خواهیم خروجی‌های شبکه را به عنوان احتمال گزینه‌ها (به عنوان مثال کلاس‌های الگو)، به شکل تابعی از ورودی‌ها، در نظر بگیریم. همچنین به دنبال پیدا کردن تابعی غیر خطی به عنوان خروجی مناسب هستیم تا معیارهای مناسب برای انطباق با پارامترهای شبکه (مثلا ضرایب وزنی برای گره‌ها) را دارا باشد.  این کار بوسیله دو تغییر اجرا می‌شود. «امتیازدهی احتمالی» (probability scoring)، که جایگزینی برای به «کمینه سازی مربع خطا» (squared error minimization) است و دیگری «نرمال سازی نمایی بیشینه هموار» (softmax) روی ورودی‌های چند متغیر از نوع لجستیک غیر خطی.

خروجی‌های حاصل برای هر ورودی، بای مثبت بوده و مجموع همه آن‌ها باید برابر با یک باشد. با توجه به مجموعه مقادیر مثل $$V_{j}$$ که بدون هیچ محدودیت در نظر گرفته می‌شوند، می‌توان این دو تغییر را با استفاده از یک «تابع نمایی نرمال شده» (Normalized Exponential transformation) به صورت زیر ایجاد کرد.

$$\large {\displaystyle Q_{j} (x) = \left.e ^{V_ {j} (x)} \right/ \sum_ {k} e ^ {V_{k} (x)}}$$

رابطه ۴

این تغییرات را می‌توان یک تعمیم از لجستیک با ورودهای چند متغیره در نظر گرفت که روی کل لایه خروجی اعمال می‌شود. به این ترتیب رتبه مقادیر ورودی حفظ شده و یک تعمیم جدید برای پیدا کردن مقدار حداکثر ارائه می‌دهد. به همین دلیل از واژه «بیشینه هموار» (Softmax) برای آن استفاده می‌کنیم.

تابع آرگومان حداکثر

شاید به نظر نام تابع «بیشینه هموار» (softmax) قدری گمراه کننده باشد و به نظر برسد که با تابعی مواجه هستیم که به طور مجانبی به سمت مقدار حداکثر میل می‌کند. باید توجه داشت که منظور از این عبارت، اشاره به یک تابع حداکثر صاف یا هموار نیست، بلکه به کمک این تابع «آرگومان» (Argument) یا شماره (ترتیب) مقداری از دامنه تابع را پیدا می‌کنیم که تابع را حداکثر می‌کند.

فیلم آموزش یادگیری ماشین با پایتون – ماشین لرنینگ با Python در فرادرس

کلیک کنید

از طرفی مفهوم تابع بیشینه هموار کاملا با عملکرد تابع LogSumExp یا «لگاریتم مجموع عبارت‌های توانی»، ارتباط دارد. به همین دلیل گاهی افراد به جای تابع softmax از softargmax استفاده می‌کنند. البته در حوزه یادگیری ماشین بیشتر از اصطلاح softmax برای این تابع استفاده می‌شود.

این بار تعریف رسمی‌تری برای تابع softargmax معرفی می‌کنیم. ورودی‌های $$z_i$$ را به یاد دارید. فرض کنید تابع softmax یا همان softargmax این ورودی را دریافت کرده و یک بردار از مقادیر به صورت $$y_i$$ ارائه می‌دهد. به این ترتیب رابطه زیر را خواهیم داشت.

$$\large {\displaystyle \operatorname {arg \, max} (z_{1}, \cdots , z_{n}) = (y_{1} , \cdots, y_n}) = (0 , \cdots, \, 0,1 , 0 , \cdots, 0)$$

رابطه ۵

که در آن مختصات خروجی یعنی $$\displaystyle y_{i} = 1$$ است، اگر و فقط اگر $$i$$، شماره آرگومان یا مولفه‌ای باشد که مقدار حداکثر $$z$$ها را نشان می‌دهد و در بقیه موارد، مقدار $$\displaystyle y_i = 0$$ است.

برای مثال تابع arg max را برای بردار $$(1,5,10)$$ در نظر بگیرید. واضح است که رابطه زیر برقرار خواهد بود. زیرا بزرگترین مقدار بردار، سومین مقدار آن است.

$$\large{ \displaystyle \operatorname{arg\,max} (1,5,10)=(0,0,1) }$$

البته توجه داشته باشید که تابع معرفی شده، فقط در زمانی که بزرگترین مقدار تکراری نباشد، قابل استفاده است. برای برداری از مشاهدات مثل $$z_i$$ ‌احتیاج به یک تعمیم برای تعریف ارائه شده داریم تا در زمانی که مقادیر تکراری وجود داشته باشد، از آن کمک بگیریم.

به این ترتیب حالتی را در نظر بگیرید که چندین مقدار از $$z_i$$، حداکثر مقدار را داشته باشند. واضح است که همگی آن‌ها باید با یکدیگر برابر باشند. در این وضعیت، تابع argmax را برای چنین مشاهداتی از تقسیم ۱ بر تعداد مقدار حداکثر (مثل $$k$$) بدست می‌آوریم.

در نظر بگیرید که برداری به صورت $$z=(0, 5 , 5)$$ داریم. از ‌آنجایی مقدار حداکثر، دارای فراوانی به اندازه $$k=2$$ است، مقدار تابع argmax را برای آن‌ها به صورت $$1/k$$ در نظر می‌گیریم و خواهیم داشت:

$$\large {\displaystyle \operatorname {arg\, max} (0 , 5 , 5) = ( 0 , 1/2, 1/2)}$$

زیرا آرگومان دوم و سوم، مقادیر حداکثر بردار را نشان داده و تعدادشان برابر با ۲ است. پس برای هر یک از آن‌ها مقدار تابع arg max برابر با $$\dfrac{1}{2}$$ خواهد بود و برای بقیه مقادیر، صفر در نظر گرفته می‌شود.

در صورت برابر بودن همه آرگومان‌ها، به رابطه $$\displaystyle \operatorname {arg \, max} (z, \dots, z) = (1 / n, \dots, 1/​​n)$$ خواهیم رسید. واضح است که چنین تابعی، یک تابع پیوسته نبوده و در نقاط نابرابر، دارای شکستگی خواهد بود.

به این ترتیب می‌توان تابع argmax را یک تقریب هموار برای تابع softargmax در نظر گرفت. زمانی که $$\beta \to \infty$$ بهترین تقریب برای رابطه ۲، شکل می‌گیرد. البته باید توجه داشت که تابع softargmax یک تابع پیوسته است ولی تابع argmax پیوسته نیست.

به عنوان مثال، $${\displaystyle \sigma_{\beta} (1,1.0001) \to (0,1) }$$ اما $${\displaystyle \sigma_{\beta} (1, 0.9999) \to (1,0) }$$ و $$\sigma_ {\beta} (1،1) = 1/2$$.

پس برای همه ورودی‌ها، هرچه امتیازها نزدیکتر باشند به مجموعه منفرد $${\displaystyle (x، x)}$$، سرعت همگرایی کندتر می‌شود. با این حال، تابع softargmax به طور فشرده به یک در مجموعه غیر منفرد، همگرا می‌شود.

برعکس، اگر $$\beta \to -\infty$$، آنگاه تابع softargmax به کوچکترین آرگومان (arg min) همگرا خواهد بود. در اینجا، مجموعه منفرد، شامل دو مقدار حداقل است.

همچنین برای هر $$\beta$$ ثابت، اگر یک ورودی $${\displaystyle z_{i}}$$ نسبت به دما ($$T$$)، خیلی بزرگ باشد، ($$T = \dfrac{1}{\beta}$$)، آنگاه، خروجی تقریباً arg max خواهد بود. به عنوان مثال، اختلاف 10 نسبت به دمای 1 زیاد است، پس داریم:

$$\large {\displaystyle \sigma(0, 10):= \sigma_{1} (0, 10)= \left( 1/ (1 + e^{10}), e^{10} /(1 + e^{10}) \right) \approx (0.00005, 0.99995) }$$

با این حال، اگر تفاوت نسبت به دما کم باشد، مقدار خروجی نزدیک به arg max نخواهد بود. به عنوان مثال، اختلاف 10 نسبت به دمای 100، کم است و داریم:

$$\large {\displaystyle \sigma_{1/100}(0,10) = \left( 1/(1 + e^{1/10}) ,e^{ 1/10}/(1 + e^{1/10}) \right) \approx (0.475,0.525)}$$

همانطور که مشخص است، زمانی که $$\beta \to \infty$$، آنگاه $$T=\dfrac{1}{\beta} \to 0$$ و هر اختلافی، بزرگ به نظر می‌رسد. این موضوع یک دلیل مهم برای مشخص کردن رفتار حدی این تابع محسوب می‌شود.

کاربردهای تابع بیشینه هموار

همانطور که اشاره شد، تابع بیشینه هموار در مکانیک آماری و بخصوص توزیع بولتمان به کار گرفته می‌شود. در ادامه به هر یک از این بخش‌ها پرداخته و توضیحاتی در نحوه کاربرد این تابع در آن حوزه‌ها، بیان خواهیم کرد.

نظریه احتمال

در نظریه احتمال (Probability Theory) یا به طور دقیق‌تر، نظریه توزیع‌ها (Distribution Theory)، از خروجی تابع softargmax می‌توان برای نشان دادن یک توزیع طبقه‌ای- یعنی توزیع احتمال بر k نتایج مختلف، استفاده کرد. به این ترتیب یک توزیع گسسته تولید شده که هر یک از مقادیر آن، دارای احتمال برابر بوده به صورت یکنواخت (Discrite Distribution)، توزیع شده است. البته توجه داشته باشید که این مقدار احتمال فقط برای مقادیر حداکثر یک بردار تصادفی مورد محاسبه قرار می‌گیرد.

مکانیک آماری

در «مکانیک آماری» (Statistical Mechanic)، تابع softargmax به توزیع بولتزمان (یا توزیع گیبس) معروف است که در آن مجموعه $$Y: {\displaystyle {1, \ldots, k}}$$ ریزحالت‌ها (وضعیت‌های) سیستم بوده و همچنین ورودی‌های $$\displaystyle z_ {i}$$، مربوط به انرژی‌های آن حالت محسوب می‌شوند. مخرج مربوط به رابطه ۲ که به «تابع پارش» (Partition Function) معروف است، در مکانیک آماری، گاهی با Z نشان داده می‌شود. از طرفی عامل $$\beta$$ را سردی (یا بتای ترمودینامیکی یا دمای معکوس) می‌نامند.

کاربردهای مهندسی

کارشناسان و کاربران حوزه هوش مصنوعی و یادگیری ماشین، از تابع softmax در روش‌های مختلف دسته یا «طبقه‌بندی» (Classification) چند وضعیتی، مانند «رگرسیون لجستیک چند جمله‌ای» (Multinomial Logistic Regression) که گاهی به عنوان رگرسیون softmax نیز شناخته می‌شود، بهره می‌برند. همچنین  «تحلیل ممیزی خطی چند کلاسه» (Multiclass Linear Discriminant Analysis)، «دسته‌بند بیز ساده» ( Naive Bayes Classifiers) ‌و «شبکه‌های عصبی مصنوعی» (Artificial Neural Network) تکنیک‌هایی هستند که از جمله کاربردهای تابع softmax محسوب می‌شوند.

فیلم مجموعه آموزش شبکه‌ های عصبی مصنوعی – مقدماتی تا پیشرفته در فرادرس

کلیک کنید

به طور خاص، در رگرسیون لجستیک چند جمله‌ای و تجزیه و تحلیل ممیزی یا تحلیل ممیزی خطی، نتیجه محاسبات صورت گرفته توسط $$k$$ تابع خطی متفاوت، ورودی به تابع محسوب می‌شوند و احتمال پیش بینی شده برای کلاس $$j$$ام، با توجه به نمونه‌ $$x$$ و بردار وزن‌های $$w$$ به صورت زیر خواهد بود.

$$\large {\displaystyle P (y = j \mid \mathbf {x} ) = {\dfrac {e ^ {\mathbf {x} ^ {\mathsf {T}} \mathbf {w}_ {j}}} {\sum_{k = 1} ^ {K} e ^ {\mathbf {x} ^ {\mathsf {T}} \mathbf {w}_{k}}}}}$$

رابطه بالا را می‌توان یک ترکیب از $$K$$ توابع خطی و تابع بیشینه هموار به صورت زیر در نظر گرفت.

$$\large \mathbf {x} \mapsto \mathbf {x} ^{\mathsf {T}}\mathbf {w} _{1},\ldots ,\mathbf {x} \mapsto \mathbf {x} ^{\mathsf {T}}\mathbf {w} _{K}$$

نکته: توجه داشته باشید که $$X^TW$$ نشانگر ضرب داخلی دو بردار $$x$$ و $$w$$ است.

شبکه‌های عصبی

از تابع softmax اغلب در لایه نهایی تکنیک طبقه‌بندی مبتنی بر «شبکه‌های عصبی» (Neural networks) استفاده می‌شود. چنین شبکه‌هایی معمولاً تحت توابع زیان لگاریتمی (یا آنتروپی متقابل- Cross Entropy) آموزش می‌یابند و یک نوع رابطه غیرخطی از رگرسیون لجستیک چند جمله‌ای را ارائه می‌کنند.

از آنجا که این تابع یک بردار را و یک اندیس خاص مثل $$\displaystyle i$$ را به یک مقدار از اعداد حقیقی، نگاشت می‌کند، باید هنگام مشتق‌گیری به اندیس $$i$$ نیز توجه شود. در نتیجه خواهیم داشت:

$$\large \displaystyle {\dfrac {\partial} {\partial q_{k}}} \sigma ({\textbf {q}}, i) = \sigma ({\textbf {q}}, i) (\delta_ {ik} - \sigma ({\textbf {q}} ,k))$$

این عبارت نسبت به اندیس‌های $$i$$ و $$k$$‌ متقارن است،‌ در نتیجه می‌توان به شکل ساده‌تری آن را نمایش داد.

$$\large {\displaystyle {\frac {\partial }{\partial q_{k}}}\sigma ({\textbf {q}},i)=\sigma ({\textbf {q}},k)(\delta _{ik}-\sigma ({\textbf {q}},i))}$$

در اینجا ، «دلتا کرونکر» (Kronecker delta) با نماد ($$\delta_{ik}$$ برای سادگی استفاده شده است. اگر تابع با پارامتر $$\displaystyle \beta$$ مقیاس بندی شود، عبارت بالا را باید در $$\displaystyle \beta$$ ضرب کرد.

یادگیری تقویتی

در زمینه «یادگیری تقویتی» (Reinforcement learning)، می‌توان از تابع softmax برای تبدیل مقادیر به احتمال انجام عمل (Action Probability) استفاده کرد. تابعی که معمولاً استفاده می‌شود به صورت زیر است.

$$\large P_{t}(a)={\frac {\exp(q_{t}(a)/\tau )}{\sum _{i=1}^{n}\exp(q_{t}(i)/\tau )}}$$

در رابطه بالا، مقدار عمل (Action Value) به صورت  $$\displaystyle q_ {t} (a)$$ نشان داده شده و نماینگر پاداش مورد انتظار برای عمل است. از طرفی $$tau$$ نیز دمای پارامتر (در حوزه مکانیک آماری) است.

برای دماهای زیاد ($$\displaystyle \tau \to \infty$$)، همه عمل‌ها (Actions) دارای احتمال تقریبا یکسان هستند و هر چه دما کمتر شود، مقدار مورد انتظار پاداش، روی احتمال تاثیر می‌گذارد. بطوری که برای دماهای پایین ($$\displaystyle \tau \to 0^+$$)، احتمال رخداد یک عمل با بیشترین پاداش مورد انتظار، تقریبا برابر با ۱ است.

خواص تابع بیشینه هموار

از نظر هندسی تابع softmax فضای برداری $$\displaystyle \mathbb {R} ^ {K}$$ را به فضای داخلی (K-1) سیمپلکس نگاشت می‌کند. این کار بوسیله برش به یک بُعد انجام شده و براساس قیدهای خطی صورت می‌گیرد، بطوری که مجموع همه خروجی‌ها به یک برسد. این امر به این معنی است که این تابع در یک ابرصفحه (Hyperplane) قرار دارد.

در طول قطر اصلی یعنی $$(x , x , x , \ldots,x)$$، تابع بیشینه هموار دارای توزیع یکنواخت با خروجی‌های $$(1/n, 1/n ,\ldots,1/n)$$ خواهد بود. این امر به معنی هم احتمال بودن ورودی‌ها است.

در حالت کلی تابع بیشینه هموار، تحت تبدیل خطی روی هر مولفه، پایا است. به این ترتیب اگر $$C = (c,c,\ldots,c)$$ مقادیر ثابت بوده و به ورودی بردار $$z$$ اضافه شوند، آنگاه خواهیم داشت:

$$\large \sigma(z + c) = \sigma(z)$$

واضح است که در این حالت، هر عبارت توانی در فاکتور یا عامل ثابت $$e^c$$ ضرب می‌شود، زیرا برای تابع نمایی رابطه زیر از خصوصیات آن محسوب می‌شود.

$$\large {\displaystyle e^{z_{i} + c}= e^{z_{i}} \cdot e^{c}}$$

بنابراین مخرج کسر تابع بیشینه هموار تغییر نکرده و داریم:

$$\large {\displaystyle \sigma (\mathbf {z} +\mathbf {c} )_{j}={\dfrac {e^{z_{j} + c}}{\sum_{k=1}^{K}e^{z_{k}+c}}}={\dfrac {e^{z_{j}}\cdot e^{c}}{\sum_{k=1}^{K}e^{z_{k}}\cdot e^{c}}}=\sigma (\mathbf {z} )_{j}}$$

از نظر هندسی، تابع بیشینه هموار (softmax) در روی قطرها ثابت است، زیرا: این بعدی است که حذف می‌شود و بیانگر مستقل بودن تابع softmax نسبت به تبدیل روی مقادیر ورودی است. بوسیله نرمال سازی ورودی‌ها با استفاده از مقدار ثابت $$c$$ که توسط میانگین مقادیر بردار $$z$$ حاصل می‌شود، می‌توان مجموع ورودی ها را به صفر تبدیل کرد. کافی است که $$c = \frac{1}{n} \sum z_i$$ در نظر گرفته شود و هر ورودی را از $$c$$ کم کرده و به عنوان ورودی جدید در نظر گرفت.

به این ترتیب تابع softmax روی یک «ابرصفحه» (Hyperplane) با نقاطی ایجاد می‌شود که دارای مجموع صفر هستند، یعنی داریم $$\sum z_i = 0$$ و خروجی‌ها نیز دارای مجموع ۱ خواهند بود ($$\sum \sigma(z_i) = 1$$). این با توان صفر تابع نمایی ($$e^0 = 1$$) نیز مطابقت دارد.

در مقابل، تابع بیشینه هموار نسبت به تبدیل مقیاس (ضرب در یک مقدار ثابت) پایا (invariant) نیست. برای مثال رابطه زیر را در نظر بگیرید.

$$\large {\displaystyle \sigma {\bigl (}(0,1){\bigr )} = {\bigl (}1 / (1+e) , e/ (1+e) {\bigr )}}$$

از طرفی با ضرب مولفه‌های اولیه در ۲، خواهیم داشت:

$$\large {\displaystyle \sigma {\bigl (}(0,2){\bigr )} ={ \bigl (}1/(1 + e^{2}), e^{2}/( 1 + e^{2}){\bigr )}}$$

که نشانگر تغییر در خروجی‌ها است.

«تابع لجستیک استاندارد» (Standard Logistic Function) مورد خاصی برای یک محور 1 بعدی در فضای 2 بعدی است ، مثلاً محور x در صفحه (x ، y). فرض کنید که یک متغیر در 0 ثابت شده است (مثلا $$\displaystyle z_{2} = 0$$)، بنابراین $$\displaystyle e ^{0} = 1$$ و متغیر دیگر می‌تواند هر مقداری را بگیرد. اگر آن را با $$z_1 = x$$ مشخص کنیم، آنگاه، تابع لجستیک استاندارد به صورت زیر خواهد بود.

$$\large {\textstyle e^{z_{1}}/\sum_{k = 1}^{2}e^{z_{k}} = e^{x}/( e^{x} + 1)}$$

و مکمل آن (به این معنی که مجموعشان برابر با ۱ خواهد بود) به صورت زیر نوشته خواهد شد.

$$\large {\textstyle e^{z_{2}}/ \sum_{k = 1}^{2} e^{z_{k}} = 1/( e^{x} + 1) }$$

ورودی یک بُعدی را می‌توان یک خط در با رابطه $$(x/2 , -x/2)$$ در نظر گرفت، بنابراین خروجی به  صورت

$$\large {\displaystyle e^{x/2} / (e^{x/2} + e^{-x/2}) = e^{x}/ (e^{x} + 1)}$$

و

$$\large {\displaystyle e^{-x/ 2}/(e^{x /2} + e^{-x/2}) = 1/ (e^{x} + 1)}$$

در می‌آید.

تابع softmax نیز گرادیان تابع LogSumExp است، که یک هموارساز بیشینه است. چنین تابعی را به صورت زیر تعریف می‌کنیم.

$$\large {\displaystyle \operatorname {LSE} (z_{1}, \dots ,z_{n}) = \log \left( \exp(z_{1}) + \cdots + \exp(z_{n}) \right)}$$

و مشتق جزئی (گرادیان) آن به شکل زیر حاصل می‌شود.

$$\large {\displaystyle \partial_{i}\operatorname {LSE} (\mathbf {x} ) = {\dfrac { \exp x_{i} }{\sum_{i}\exp x_{i}}}}$$

چند نکته در مورد تابع بیشینه هموار

1. مقادیر مثبت برای$$\beta$$ در تابع بشینه هموار، در بیشینه سازی کاربرد داشته و معمولا در یادگیری ماشین، چنین وضعتی به کار می‌رود. به این ترتیب بزرگترین مقادیر دارای بیشترین احتمال هستند. در مقابل، مقدار منفی برای $$\beta$$ برای کمینه‌سازی به کار رفته و در ترمودینامیک به کار می‌رود. وضعیت یا حالت کمترین انرژی با بیشترین احتمال در این حالت بدست می‌آید. این امر همان تعبیر سرید (Coldness) برای $$\beta$$ در توزیع گیبس است.
2. نماد $$\beta$$ از ترمودینامیک بتا گرفته شده است که نمایانگر معکوس دمای ترمودینامیکی است. در این حالت داریم: $$\beta = 1/ T , T = 1/\beta$$.
3. زمانی که $$\beta=0$$ (سرمای صفر یا دمای بی‌نهایت)، خواهیم داشت: $$b = e^{\beta} = e^ 0 = 1$$ و باعث ایجاد مقادیر ثابت در تابع بیشینه هموار ($$1/n ,\ldots , 1/n$$) می‌شود که با «توزیع یکنواخت گسسته» (Discrete Uniform Distribution) یکسان است.
4. در مکانیک آماری، ثابت بودن $$\beta$$ به عنوان دما یا سرمای ۱ تلقی می‌شود.

مثال برای محاسبه تابع بیشینه هموار به زبان‌های برنامه‌نویسی مختلف

طی یک مثال و کدنویسی به زبان‌های پایتون، جولیا و R، محاسبات و بدست آوردن تابع بیشینه هموار را در این قسمت مرور می‌کنیم. یک ورودی مانند ورودی [1 ، 2 ، 3 ، 4 ، 1 ، 2 ، 3] را بگیرید. این بخش نشانگر بردار ورودی (z) است. نرم افزار یا برنامه‌های نوشته شده نتایجی به صورت بردار [0.024 ، 0.064 ، 0.175 ، 0.475 ، 0.024 ، 0.064 ، 0.175] تولید خواهند کرد که همان $$\delta(z)$$ است. واضح است که مجموع مقادیر خروجی (تقریبا) برابر با ۱ است.

خروجی بیشترین وزن خود را در جایی دارد که مقدار ورود ۴ باشد، حاصل می‌کند. این همان چیزی است که به طور معمول از این تابع انتظار داریم: «برجسته کردن بزرگترین مقادیر و سرکوب مقادیری که به طور قابل توجهی زیر حداکثر مقدار هستند».

اما توجه داشته باشید که تابع softmax نسبت به تغییر مقیاس (ضرب کردن در یک مقدار ثابت) پایا نیست. بنابراین اگر ورودی $$z$$ به صورت [0.1 ، 0.2 ، 0.3 ، 0.4 ، 0.1 ، 0.2 ، 0.3] در آید ( یعنی همه مولفه بردار به ۱۰ تقسیم شوند) آنگاه نتیجه تابع به صورت [0.125 ، 0.138 ، 0.153 ، 0.169 ، 0.125 ، 0.138 ، 0.153] خواهد بود. البته باز هم مشخص است که مجموع خروجی‌های تابع برابر با یک خواهد بود. ولی به هر حال مشخص است که با کوچک کردن (استاندارد کردن) مقادیر در بازه ۰ تا ۱ مقادیر تابع بیشینه هموار، فاصله را حفظ نکرده و خروجی‌ها به هم نزدیکی خواهند شد. توجه داشته باشید که 0٫169 نه تنها کمتر از 0٫455 است ، بلکه حتی از نسبت ۰٫۴ به جمع کل مقادیر ورودی نیز کمتر است.

$$\large 0.4 / 1.6 = 0.25, \;\;\; 0.169< 0.25$$

این امر نشان می‌دهد که در صورت وجود مقادیر همشکل و یکدست، تابع بیشینه هموار، روی مقادیر بزرگتر تاکید کمتری خواهد داشت.

محاسبه این مثال با استفاده از کد پایتون

در کدی که به زبان پایتون مشاهده می‌کنید، از کتابخانه numpy استفاده شده و یک بردار به نام a در نظر گرفته شده نتیجه اجرای محاسبات و تولید پاسخ برای تابع softmax نیز در انتهای کد به صورت یک خط خروجی دیده می‌شود.

1>>> import numpy as np
2>>> a = [1.0, 2.0, 3.0, 4.0, 1.0, 2.0, 3.0]
3>>> np.exp(a) / np.sum(np.exp(a)) 
4array([0.02364054, 0.06426166, 0.1746813, 0.474833, 0.02364054,
5       0.06426166, 0.1746813])

محاسبه این مثال با استفاده از کد جولیا

عملیات گفته شده را به زبان جولیا در کدهای زیر مشاهده می‌کنید. این بار هم بردار در متغیر A ثبت شده و محاسبات با نمایش عناصر بردار محاسبه شده نمایش داده شده است.

1julia> A = [1.0, 2.0, 3.0, 4.0, 1.0, 2.0, 3.0];  # semicolon to suppress interactive output
2
3julia> exp.(A) ./ sum(exp.(A))
47-element Array{Float64,1}:
5 0.0236405
6 0.0642617
7 0.174681
8 0.474833
9 0.0236405
10 0.0642617
11 0.174681

محاسبه این مثال با استفاده از کد R

کدی که در ادامه مشاهده می‌کنید، به زبان برنامه‌نویسی R و برای بدست آوردن تابع «بیشینه هموار» (Softmax) به کار گرفته شده. ساختار فرمول و محاسبات انجام شده مطابق با رابطه ۲ است.

مشخص است که نتیجه بدست آمده با نتایج حاصل از زبان‌های برنامه‌نویسی دیگر نیز مطابقت دارد.

1> z <- c(1.0, 2.0, 3.0, 4.0, 1.0, 2.0, 3.0)
2> softmax <- exp(z)/sum(exp(z))
3> softmax
4[1] 0.02364054 0.06426166 0.17468130 0.47483300 0.02364054 0.06426166 0.17468130

خلاصه و جمع بندی

یکی از توابع مهم در یادگیری ماشین و همینطور ترمودینامیک آماری، تابع بیشینه هموار (softmax) است که به عنوان ابزاری برای توزیع بولتزمان به کار می‌رود. با توجه به ارتباط نزدیک این تابع و توزیع، متن پیش رو، تهیه و تنظیم گردید. ارتباط تابع softmax و softargmax همچنین رفتار حدی تابع arg max نیز مورد بررسی قرار گرفت. ارتباط تابع بیشینه هموار با نظریه احتمال و همچنین مکانیک یا ترمودینامیک آماری نیز در طی این نوشتار مورد بررسی و بحث قرار گرفت.