تابع بتا — از صفر تا صد
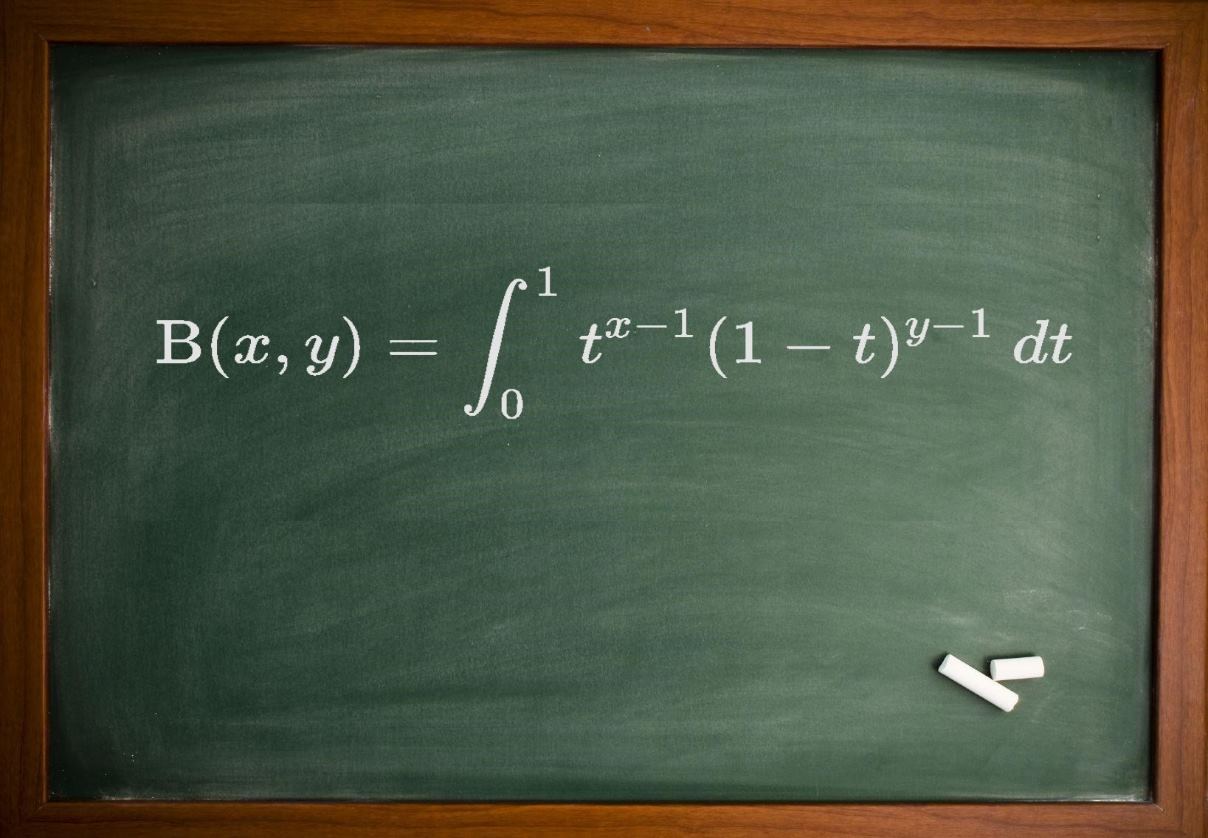
پیشتر و در مطلبی در وبلاگ فرادرس در مورد تابع گاما صحبت شد. در مطلب مذکور بیان کردیم که در ریاضی دو نوع انتگرال اویلری داریم که نوع دوم آن همان تابع گاما است. در این مطلب قصد داریم تا انتگرال نوع اول اویلر یا همان تابع بتا را معرفی کرده و ویژگیهای آن را توضیح دهیم.
تعریف تابع بتا
در ریاضیات تابع بتا یا همان انتگرال اویلر نوع اول، تابعی خاص است که مطابق با رابطه زیر تعریف میشود.
$$ { \displaystyle \mathrm { B } ( x , y ) = \int _ { 0 } ^ { 1 } t ^ { x - 1 } ( 1 - t ) ^ { y - 1 } \, d t } $$
توجه داشته باشید که در رابطه فوق، $$ x , y $$ میتوانند حتی مقادیری مختلط نیز باشند؛ همچنین بخشهای حقیقی این دو مقدار، مثبت هستند ($$ \ { R e } \ x > 0 , \ { R e } \ y > 0 $$). این تابع توسط اویلر و لژاندر مطالعه شده ولی اسم آن توسط «ژاک بینت» (Jacques Philippe Marie Binet) نامگذاری شده است. در ادامه نمونهای از کانتور تابع بتا ارائه شده است.
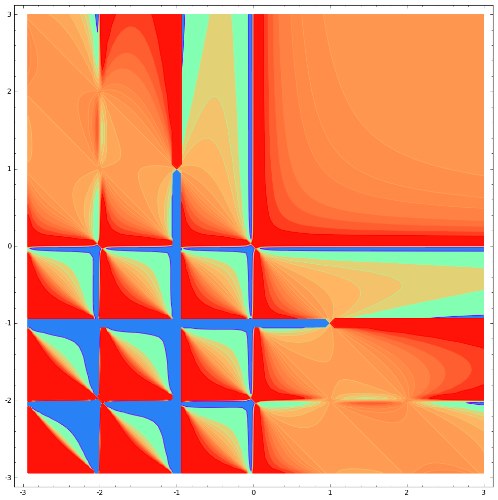
ویژگیها
تابع بتا متقارن است؛ این جمله به معنای آن است که با تغییر ترتیب $$ x $$ و $$ y $$، شکل کلی تابع تغییر نمیکند. بنابراین عبارت ریاضی زیر را میتوان در مورد تابع بتا بیان کرد:
$$ { \displaystyle \mathrm { B } ( x , y ) = \mathrm { B } ( y , x ) . } $$
تابع بتا را میتوان بر حسب تابع گاما مطابق با رابطه زیر بیان کرد:
$$ { \displaystyle \mathrm { B } ( x , y ) = { \frac { \Gamma ( x ) \, \Gamma ( y ) } { \Gamma ( x + y ) } } } $$
بهمنظور اثبات رابطه فوق از تعریف تابع گاما استفاده میکنیم. دو تابع $$ \Gamma ( x ) $$ و $$ \Gamma ( y ) $$ را در نظر بگیرید. حاصلضرب این دو تابع را میتوان با توجه به تعریف بهصورت زیر بیان کرد:
$$ { \displaystyle {\begin{aligned}\Gamma (x)\Gamma (y)&=\int _ { u = 0 } ^ { \infty } \ e ^ { - u } u ^ { x - 1 } \,du\cdot \int _ { v = 0
} ^ { \infty } \ e ^ { - v } v ^ { y - 1 } \, d v \\[6pt]&=\int _ { v = 0 } ^ { \infty }\int _ { u = 0 } ^ { \infty } \ e ^ { - u - v } u ^ { x - 1 } v ^ { y - 1 } \,du\,dv.\end {aligned} } } $$
برای حل انتگرال فوق از تغییر متغیرهای $$ u = f ( z , t ) = z t $$ و $$ v = g ( z , t ) = z ( 1 − t ) $$ استفاده میکنیم. با استفاده از این تغییر متغیرها، حاصل انتگرال فوق را میتوان مطابق با عبارت زیر بر حسب تابع بتا بیان کرد:
$$ { \displaystyle {\begin{aligned}\Gamma (x)\Gamma (y)&=\int _ { z = 0 } ^ { \infty }\int _ {t = 0 } ^ { 1} e ^ { - z} ( z t ) ^{ x - 1 } ( z ( 1 -t))^{y-1}{\big | } J ( z , t ) { \big |} \,dt\,dz\\[6pt]&=\int _{z=0}^{\infty }\int _ { t = 0 }^ { 1 } e^ {- z } ( z t ) ^ { x- 1 } ( z( 1 - t) ) ^ { y -1 } z \,dt\,dz\\[6pt]&=\int _{z=0}^{\infty }e^{-z}z^{x+y-1}\,dz\cdot \int _{t=0 } ^ { 1 } t^ { x - 1 }( 1 - t) ^ { y - 1 } \,dt\\&=\Gamma (x+y)\,\mathrm { B } ( x , y ),\end{aligned}}} $$
در اثبات انجام شده در بالا $$ | J ( z , t ) | $$ نشاندهنده ژاکوبین دو ماتریس $$ u = f ( z , t ) $$ و $$ v = g ( z , t ) $$ است. در اکثر کاربردهای تابع بتا، مشتقات آن نیز ظاهر میشوند. معمولا برای محاسبه مشتق از تابعی تحت عنوان دایگاما استفاده میشود. برای نمونه مشتق تابع بتا نسبت به $$ x $$، مطابق با رابطه زیر بدست میآید.
$${ \displaystyle {\frac {\partial } { \partial x } } \mathrm { B } ( x , y ) = \mathrm { B } ( x , y ) \left ( { \frac { \Gamma ^ { \prime } ( x ) } { \Gamma ( x ) } } – { \frac { \Gamma ^ { \prime } ( x + y ) } { \Gamma ( x + y ) } } \right ) = \mathrm { B } ( x , y ) { \big ( } \psi ( x ) – \psi ( x + y ) { \big ) } }$$
در رابطه بالا $$ ψ ( x ) $$ نشاندهنده تابع دایگاما است (در مطالب آینده این تابع را نیز توضیح خواهیم داد).
در حالت کلی میتوان روابط زیر را میان دو تابع گاما و بتا بیان کرد:
$$ { \displaystyle { \begin {aligned} \mathrm { B } ( x , y ) & ={ \dfrac { ( x - 1 ) ! \, ( y - 1 ) ! }{ ( x + y - 1 ) ! } } \\[6pt]\mathrm { B } ( x , y ) & = 2 \int _ { 0 } ^ { \pi /2} ( \sin \theta ) ^ { 2 x - 1 } ( \cos \theta )^ {2y-1}\,d\theta ,&&\operatorname { R e } ( x ) > 0 ,\ \operatorname {Re} (y)>0\\[6pt]\mathrm {B} (x,y)&=\int _{0}^{\infty }{\frac { t ^ { x - 1 } } { ( 1 + t ) ^ { x + y } } } \,dt,&&\operatorname {Re} (x)>0,\ \operatorname { Re} (y)>0\\[6pt]\mathrm { B } (x,y)&=n\int _ {0 } ^ { 1} t ^ { n x - 1 } ( 1 - t ^ { n } ) ^ { y - 1 } \, d t ,&&\operatorname {Re} (x)>0,\ \operatorname { Re } ( y ) > 0 ,\ n > 0 \\[6pt]\mathrm {B} (x,y)&=\sum _{n=0}^{\infty }{\frac {\binom {n-y } { n } } { x + n } } \\[6pt]\mathrm {B} (x,y)&={\frac { x + y } { x y
} } \prod _ { n = 1 } ^ { \infty }\left(1+{\dfrac {xy}{ n ( x +y + n ) }} \right ) ^ { - 1 } \end{aligned} } } $$
در حالتی که ورودی یا خروجی توابع تغییر کنند، میتوان روابط زیر را بین قبل و بعد از این تغییر متغیرها بیان کرد:
$$ { \displaystyle { \begin {aligned} \mathrm { B } ( x , y ) & = \mathrm { B } ( x , y + 1 ) + \mathrm { B } ( x + 1 , y ) \\[6pt]\mathrm { B } (x+1,y)&=\mathrm {B} (x,y)\cdot {\dfrac { x } { x + y } } \\[6pt]\mathrm { B } (x,y+1)&=\mathrm { B } ( x , y ) \cdot {\dfrac {y}{x+y}}\\[6pt]\mathrm { B } ( x , y ) &\cdot \left(t\mapsto t_{+}^{x+y-1}\right)={\Big (}t\mapsto t _ { + } ^ { x - 1 } { \Big )}*{\Big (}t\mapsto t_{+}^{y-1}{\Big )}& & x \geq 1,y\geq 1,\\[6pt]\mathrm {B} (x,y)&\cdot \mathrm {B} ( x + y ,1 - y ) = { \frac {\pi }{x\sin(\pi y)}}\\[6pt]\mathrm {B} (x,1-x)&={\dfrac { \pi } { \sin(\pi x ) } } \\[6pt]\mathrm {B} (1,x)&={\dfrac { 1 } { x } } \end {aligned} } } $$
در روابط فوق، $$ t ↦ t ^ x _ + $$، تابع توان کوتاه شده و علامت ستاره نیز کانولوشن را نشان میدهد. با استفاده از تقریب استرلینگ نیز میتوان در حالتی که $$ x , y $$ به اندازه کافی بزرگ هستند، حاصل تقریبی تابع بتا را بدست آورد. این تابع در ادامه ارائه شده است.
$$ { \displaystyle \mathrm { B } ( x , y ) \sim { \sqrt { 2 \pi } } { \frac { x ^ { x-1 / 2 } y ^ { y - 1 / 2 } } { ( { x + y } ) ^ { x + y - 1 / 2 } } } } $$
در حالتی که مقدار $$ x $$ به اندازه کافی بزرگ باشد نیز میتوان از تقریب زیر استفاده کرد.
$$ \mathrm { B } ( x , y ) \sim \Gamma ( y ) \, x ^ { - y } $$
تابع بتای ناکامل
تابع بتای ناکامل در حقیقت شکل کلی تابع بتا محسوب شده که بهصورت زیر تعریف میشود.
$$ { \displaystyle \mathrm { B } ( x ; \, a , b ) = \int _ { 0 } ^ { x } t ^ { a - 1 } \, ( 1 - t ) ^ { b - 1 } \, d t } $$
بدیهی است که به ازای $$ x = 1 $$ تابع بتای ناکامل همان تابع بتای کامل میشود. مفهومی تحت عنوان تابع بتای ناکامل منظمشده را نیز میتوان بر حسب تابع بتای ناکامل و مطابق با عبارت زیر تعریف کرد:
$$ { \displaystyle I _{ x } ( a , b ) = { \frac { \mathrm { B } ( x ; \, a , b ) } { \mathrm { B } ( a , b ) } } } $$
تابع بتای ناکامل منظمشده یک تابع توزیع تجمعی از توزیع بتا محسوب میشود. این توزیع مربوط به متغیر تصادفی $$ X $$ بوده که در آن احتمال موفقیت برابر با $$ p $$ و اندازه نمونه نیز برابر با $$ n $$ است.
$$ { \displaystyle F ( k ;\, n , p ) = \Pr \left ( X \leq k \right ) = I _ { 1 - p } ( n - k , k + 1 ) = 1 - I _ { p } ( k + 1 , n -k ) } $$
مهمترین ویژگیهای تابع بتای ناکامل در ادامه ارائه شدهاند.
$$ { \displaystyle { \begin {aligned} I _ { 0 } ( a , b ) & = 0 \\ I _ { 1 } ( a , b ) & = 1 \\ I _ { x } ( a , 1 ) & =x ^ { a } \\ I _ { x } ( 1 , b ) & = 1 - ( 1 - x ) ^ { b } \\ I _ { x } ( a , b ) & = 1 - I _ { 1 - x} ( b, a ) \\ I _ { x } ( a + 1 , b ) & = I _ { x} (a , b )- { \frac { x ^ { a } ( 1 -x ) ^{ b } } { a \mathrm { B } ( a , b) } } \\ I _ { x }( a , b + 1 ) & = I _ { x } ( a , b ) + { \frac { x ^ { a } ( 1 -x ) ^ { b } } { b \mathrm { B } ( a , b ) } } \\ \mathrm { B } ( x ; a , b ) & = ( - 1 ) ^ { a } \mathrm {B} \left ( { \frac { x } { x- 1 } } ;a , 1 - a - b \right ) \end{aligned}}} $$
در آینده در مورد توزیعی تحت عنوان دیریکله بحث خواهیم کرد. در این توزیع از تابع بتا استفاده شده است.










