پیاده سازی شبکه عصبی پرسپترون یک لایه در پایتون

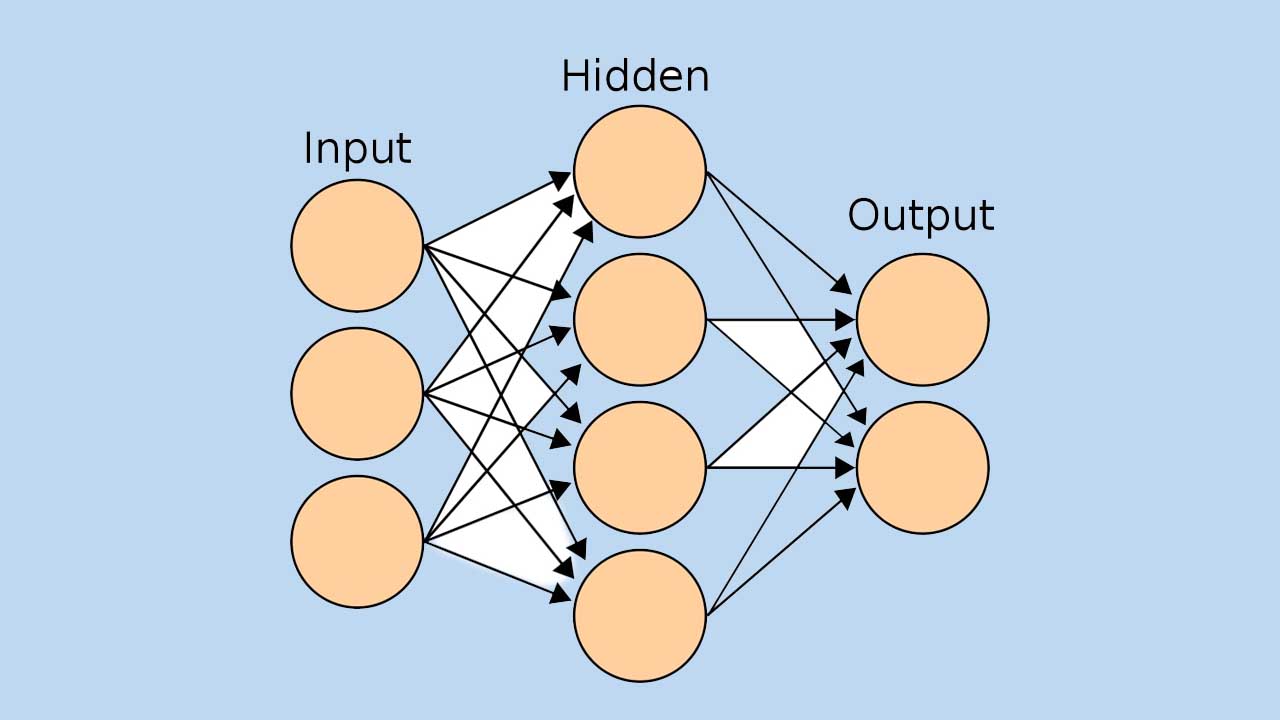
در مطلب پیاده سازی شبکه عصبی SOM در پایتون – راهنمای گام به گام به پیاده‌سازی شبکه عصبی SOM یا Self-Organizing Map پرداختیم که یک روش نظارت‌نشده (Unsupervised) بود و برای استخراج ویژگی استفاده می‌شود. در این مطلب قصد داریم پیاده سازی شبکه عصبی پرسپترون یک لایه در پایتون را بررسی کنیم. این شبکه یک الگوریتم نظارت‌شده (Supervised) است که می‌تواند برای اهداف مختلف از جمله رگرسیون (Regression) و طبقه‌بندی (Classification) استفاده شود.

دانلود فایل پیاده سازی شبکه عصبی پرسپترون یک لایه در پایتون

با توجه به دشوار بودن مراحل پیاده سازی شبکه عصبی پرسپترون یک لایه در پایتون و امکان بروز خطا، فایل‌های آماده آن در لینک زیر قابل دریافت هستند.

• برای دانلود فایل پیاده سازی شبکه عصبی پرسپترون یک لایه در پایتون + اینجا کلیک کنید.

پرسپترون چیست؟

پرسپترون (Perceptron) یک واحد مصنوعی است که براساس نورون‌های (Neuron) مغز انسان طراحی شده است. در شکل زیر نمای کلی یک نورون طبیعی را مشاهده می‌کنید:

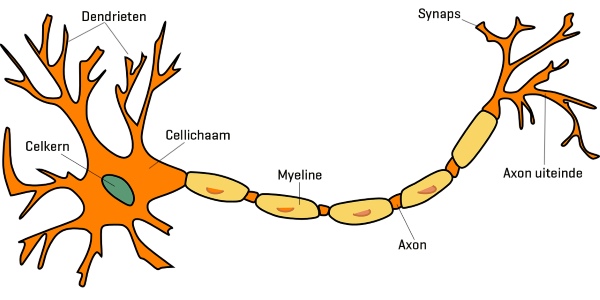
یک نورون دارای 3 بخش است:

1. دندریت‌ها (Dendrite): در این بخش، نورون سیگنال و پیام‌هایی را از نورون‌های دیگر دریافت می‌کند.
2. آکسون‌ها (Axon): در این بخش، نورون سیگنال و پیام خود را به نورون‌های دیگر انتقال می‌دهد.
3. هسته (Nucleus): این بخش و سایر بخش‌های موجود بین دندریت و آکسون در پردازش سیگنال‌ها و پیام‌ها نقش دارند.

ارتباط بین دو نورون توسط «سیناپس» (Synapse) برقرار می‌شود. این ارتباط، سیگنال نورون «پیش‌سیناپسی» (Pre-Synaptic) را به نورون «پس‌سیناپسی» (Post-Synaptic) انتقال می‌دهد.

براساس این موارد، نورون‌های مصنوعی با الهام از نورون‌های طبیعی در محیط کامپیوتر ایجاد شدند. در شکل زیر یک نورون مصنوعی یا پرسپترون را مشاهده می‌کنید:

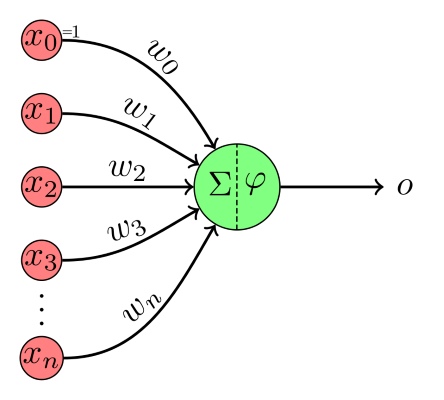
این پرسپترون به شکل زیر عمل می‌کند:

1. در ورودی یک بردار $$x$$ از لایه قبل دریافت می‌شود.
2. بردار $$x$$ در بردار $$w$$ که شامل وزن هر ورودی است، ضرب می‌شود. این وزن‌ها نقش سیناپس‌ها را ایفا می‌کنند.
3. مقدار حاصل با یک عدد ثابت به نام بایاس که با نماد b نشان داده می‌شود، جمع می‌شود. توجه داشته باشید که در برخی موارد، بایاس را با نام $$w_0$$ در نظر می‌گیرند و ورودی متناظر با آن یعنی $$x_0$$ را همواره برابر با ۱ در نظر می‌گیرند.
4. خروجی حاصل تا این مرحله را Z می‌نامیم و آن را وارد تابع $$\phi$$ می‌کنیم. این تابع با نام Activation Function یا تابع فعال‌سازی شناخته می‌شود.
5. در نهایت مقدار $$o$$ به عنوان خروجی به لایه بعد داده می‌شود.

فرآیند گفته شده را می‌توانیم به زبان ریاضی نیز بنویسیم:

$$o=\varphi(z)=\varphi\left(w^T x+b\right)=\varphi(w \cdot x+b)=\varphi\left(b+\sum_{i=1}^n w_i \times x_i\right)$$

در این رابطه، $$w$$ بردار وزن‌های بین لایه قبل و نورون موجود در لایه فعلی است. بردار $$x$$ نیز بردار خروجی لایه قبل را نشان می‌دهد. b یک عدد بوده و بایاس را نشان می‌دهد. توجه داشته باشید که $$z$$ برآیند سیگنال ورودی به نورون را نشان می‌دهد یک ترکیب خطی از سیگنال خروجی لایه قبلی است.

فیلم آموزش رگرسیون خطی و شبکه عصبی MLP در پایتون برای پیش بینی چربی بدن (رایگان) در فرادرس

کلیک کنید

به این ترتیب می‌توان نورون‌های مصنوعی را به کمک روابط ریاضیاتی توصیف کرد. یک پرسپترون به تنهایی دارای ظرفیت یادگیری (Learning Capacity) محدودی است. از این رو شبکه‌ای از پرسپترون‌ها را ایجاد می‌کنیم تا به ظرفیت یادگیری مورد نیازمان دست یابیم.

نورون‌ها می‌توانند به صورت موازی در کنار هم قرار گیرد و یک لایه را ایجاد کنند. در حالت دیگر نیز نورون‌ها می‌توانند به صورت متوالی پشت سر هم در لایه‌های مختلف قرار گیرند. بسته به ماهیت مسئله، به هر کدام از این حالت‌ها نیاز داریم.

پیاده سازی شبکه عصبی پرسپترون یک لایه در پایتون

برای پیاده‌سازی شبکه، وارد محیط برنامه‌نویسی می‌شویم و کتابخانه‌های مورد نیاز را فراخوانی می‌کنیم:

1import numpy as np
2import matplotlib.pyplot as plt

کتابخانه Numpy به منظور محاسبات ریاضیاتی شبکه و ذخیره وزن‌ها مناسب است.

کتابخانه Matplotlib نیز برای مصورسازی (Visualization) مجوعه داده (Dataset) و نمایش نتایج شبکه عصبی استفاده خواهد شد.

ایجاد کلاس

برای پیاده‌سازی مدل، از کلاس‌ها (Class) استفاده خواهیم کرد. کلاس مربوط به پرسپترون تک لایه را ایجاد می‌کنیم:

1class SLP:

متد سازنده

در اولین قدم از پیاده‌سازی کلاس مورد نظر، متد (Method) سازنده را تعریف می‌کنیم. این متد در ورودی تعداد نورون لایه پنهان (Hidden Layer) و تابع فعال‌سازی این لایه را دریافت می‌کند:

1    def __init__(self,
2                 nH:int,
3                 Activation:str):

توجه داشته باشید که چون در این مطلب قصد داریم از شبکه برای رگرسیون استفاده کنیم، تابع فعال‌سازی لایه آخر حتماً خطی (Linear) خواهد بود، بنابراین نیاز نیست برای این لایه نیز متغیری جداگانه تعریف کنیم.

حال تعداد نورون‌های لایه مخفی را در شی ذخیره می‌کنیم:

1    def __init__(self,
2                 nH:int,
3                 Activation:str):
4        self.nH = nH

حال باید تابع فعال‌سازی را بررسی کنیم. برای این شبکه قصد داریم تو تابع فعال‌سازی ReLU یا Rectified Linear Unit و Leaky-ReLU یا Leaky Rectified Linear Unit را اضافه کنیم. این دو تابع فعال‌سازی به شکل زیر تعریف می‌شود:

$$\begin{aligned} &\operatorname{ReLU}(x)=\max (x, 0)= \begin{cases}x & x \geq 0 \\ 0 & x<0\end{cases}\\ &\operatorname{LReLU}(x)=\max (x, \alpha \times x)=\left\{\begin{array}{cc} x & x \geq 0 \\ \alpha \times x & x<0 \end{array}\right. \end{aligned}$$

برای Leaky-ReLU اغلب ضریب $$\alpha$$ برابر با $$0.02$$ تنظیم می‌شود. نمودار این دو تابع به شکل زیر است:

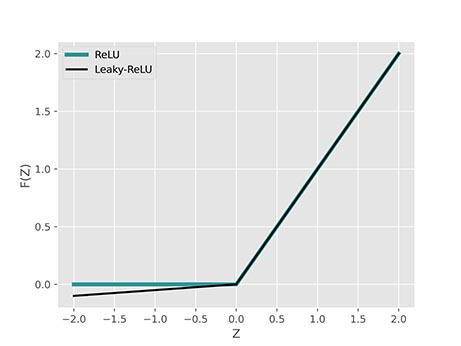
توجه داشته باشید که تابع Leaky-ReLU به دلیل داشتن مشتق غیرصفر برای ورودی‌های منفی، می‌تواند باعث یادگیری سریع‌تر شبکه شود.

دو تابع فعال‌سازی را می‌توانیم با اندکی تغییر در صورت معادله، به شکل زیر نیز تعریف کنیم:

$$\begin{aligned} &\operatorname{ReLU}(x)=\frac{x+|x|}{2} \\ &\operatorname{LReLU}(x)=\frac{(1+\alpha) \times x+(1-\alpha) \times|x|}{2}=\operatorname{ReLU}(x)+\alpha \frac{x-|x|}{2} \end{aligned}$$

به این ترتیب با یک ضابطه نیز می‌توانیم آن‌ها را توصیف کنیم. حال تابع فعال‌سازی را نیز با استفاده از lambda تعریف می‌کنیم:

1    def __init__(self,
2                 nH:int,
3                 Activation:str):
4        self.nH = nH
5        if Activation == 'relu':
6            self.Activation = lambda x: (x + np.abs(x)) / 2
7        elif Activation == 'l-relu':
8            self.Activation = lambda x: (1.02 * x + 0.98 * np.abs(x)) / 2

برای آموزش شبکه عصبی، نیاز به مشتق توابع فعال‌سازی نیز داریم. به این منظور می‌توانیم مشتق هر تابع را نیز محاسبه کنیم. در این صورت روند محاسبه به شکل زیر خواهد بود:

$$x=\varphi^{-1}(y) \rightarrow y^{\prime}=\varphi^{\prime}(x)$$

توجه داشته باشید که تنها معلوم موجود $$y$$ یعنی خروجی نورون است. به دلیل هزینه‌بر بودن محاسبه ورودی و تبدیل آن به مشتق، از یک تکنیک استفاده می‌کنیم. تابعی را تعریف می‌کنیم که با گرفتن $$y$$ در ورودی، مقدار $$y^ \prime$$ را در خروجی برگرداند:

$$y^{\prime}=\varphi^{\prime}\left(\varphi^{-1}(y)\right)=\omega(y)$$

به این ترتیب حجم محاسبات کاهش خواهد یافت. برای دو تابع فعال‌سازی گفته شده در فوق، تابع $$w$$ به شکل زیر است:

$$\begin{aligned} &\omega_{R e L U}(y)=\frac{1+\frac{y}{|y|}}{2}=\frac{1+\operatorname{sign}(y)}{2} \\ &\omega_{L R e L U}(y)=(1-\alpha) \times \frac{1+\frac{y}{|y|}}{2}+\alpha=(1-\alpha) \times \frac{1+\operatorname{sign}(y)}{2}+\alpha \end{aligned}$$

به این ترتیب این دو تابع می‌توانند مشتق خروجی نورون را با داشتن مقدار خروجی محاسبه کنند. این دو تابع را نیز به متد سازنده اضافه می‌کنیم:

1    def __init__(self,
2                 nH:int,
3                 Activation:str):
4        self.nH = nH
5        if Activation == 'relu':
6            self.Activation = lambda x: (x + np.abs(x)) / 2
7            self.dActivation = lambda y: (np.sign(y) + 1) / 2
8        elif Activation == 'l-relu':
9            self.Activation = lambda x: (1.02 * x + 0.98 * np.abs(x)) / 2
10            self.dActivation = lambda y: 0.98 * (np.sign(y) + 1) / 2 + 0.02

به این ترتیب متد سازنده کامل می‌شود.

فیلم آموزش یادگیری عمیق در پایتون با تنسورفلو و کراس TensorFlow و Keras در فرادرس

کلیک کنید

متد ایجاد پارامترها در پیاده سازی شبکه عصبی پرسپترون یک لایه در پایتون

در شروع آموزش مدل برای پیاده سازی شبکه عصبی پرسپترون یک لایه در پایتون، نمی‌توانیم در مورد مقادیر پارامترها (Parameter) اظهار نظر کنیم، به همین دلیل در ابتدای مسئله از مقادیر تصادفی به عنوان مقادیر پارامترها استفاده می‌کنیم. این متد بعد از فراخوانی، 4 آرایه برای وزن‌ها و بایاس‌ها ایجاد خواهد کرد:

1    def InitializeParameters(self):
2        self.W1 = np.random.uniform(low=-2,
3                                    high=+2,
4                                    size=(self.nX, self.nH))
5        self.B1 = np.random.uniform(low=-2,
6                                    high=+2,
7                                    size=(self.nH, ))
8        self.Wo = np.random.uniform(low=-2,
9                                    high=+2,
10                                    size=(self.nH, self.nY))
11        self.Bo = np.random.uniform(low=-2,
12                                    high=+2,
13                                    size=(self.nY, ))

توجه داشته باشید که بین لایه ورودی (Input Layer) و لایه پنهان (Hidden Layer) یک مجموعه وزن وجود دارد که با نام $$W_1$$ آن‌ها می‌شناسیم. بین لایه پنهان و لایه خروجی (Output Layer) نیز مجموعه دیگری از وزن‌ها وجود دارد که با نام $$W_0$$ می‌شناسیم. به جز وزن‌ها، دو آرایه برای بایاس‌ها نیز داریم. برای هر دو لایه پنهان و خروجی، دو آرایه با نام‌های $$B_1$$ و $$B_0$$ خواهیم داشت که مقادیر بایاس را در خود ذخیره خواهند کرد.

برای مقداردهی اولیه (Initialization) همه این پارامترها، از اعداد تصادقی (Random) با توزیع یکنواخت (Uniform) در بازه $$[-2, +2]$$ استفاده می‌کنیم. مقداردهی اولیه وزن‌های شبکه‌های عصبی، مقوله مفصلی بوده و در این زمینه مطالعات فراوانی انجام شده است. بسته به نوع مدل (Model) و پیچیدگی آن، می‌توان از روش‌های مختلفی استفاده کرد.

در مورد ابعاد این آرایه‌ها نیز باید به نکات زیر توجه کرد:

1. آرایه‌های وزن ارتباط بین دو لایه از شبکه را توصیف می‌کنند، بنابراین باید دو بُعدی باشند.
2. آرایه‌های بایاس مربوط نورون‌های یک لایه هستند، بنابراین باید یک بُعدی باشند.
3. سایز اولین بُعد هر آرایه وزن برابر با تعداد نورون لایه مبدأ است.
4. سایز دومین بُعد هر آرایه وزن برابر با تعداد نورون لایه مقصد است.
5. سایز هر آرایه بایاس برابر با تعداد نورون لایه مربوط است.

توجه داشته باشید که تعداد ورودی‌های شبکه برابر با تعداد خروجی‌های لایه ورودی است و داخل کد با مقدار self.nX نشان داده خواهد شد. تعداد خروجی‌های شبکه نیز برابر با تعداد خروجی‌های لایه خروجی است و داخل کد با مقدار self.nY نشان داده خواهد شد. این دو متغیر داخل متد Fit تعریف خواهند شد.

متد انتشار رو به جلو

شبکه عصبی، با دریافت یک بردار در لایه ورودی، به ترتیب مقدار خروجی هر لایه را تا انتها به ترتیب محاسبه می‌کند تا خروجی نهایی مدل حاصل شود. به عبارتی اطلاعات ورودی رو به جلو حرکت می‌کنند. به این فرآیند انتشار رو به جلو (Forward Propagation) گفته می‌شود. در شکل زیر مسیر انتشار اطلاعات نشان داده شده است:

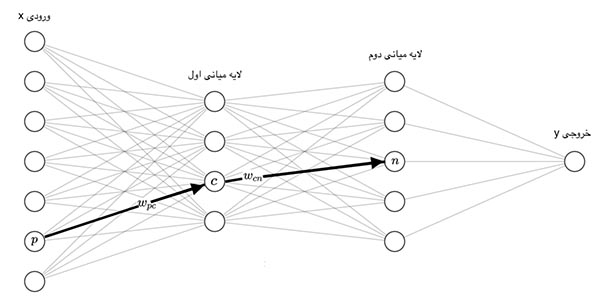
حال متدی برای انجام این فرآیند ایجاد می‌کنیم. این متد در ورودی بردارهای داده را دریافت خواهد کرد:

1    def fPropagate(self,
2                   X:np.ndarray) -> tuple:

حال می‌توانیم سیگنال ورودی به هر نورون لایه پنهان را محاسبه کنیم:

1    def fPropagate(self,
2                   X:np.ndarray) -> tuple:
3        Z1 = np.dot(X, self.W1) + self.B1

با اعمال تابع فعال‌سازی به Z1 می‌توانیم خروجی لایه پنهان را به دست آوریم:

1    def fPropagate(self,
2                   X:np.ndarray) -> tuple:
3        Z1 = np.dot(X, self.W1) + self.B1
4        O1 = self.Activation(Z1)

حال می‌توانیم سیگنال ورودی به نورون‌های لایه خروجی را محاسبه کنیم:

1    def fPropagate(self,
2                   X:np.ndarray) -> tuple:
3        Z1 = np.dot(X, self.W1) + self.B1
4        O1 = self.Activation(Z1)
5        Zo = np.dot(O1, self.Wo) + self.Bo

لایه خروجی، از تابع فعال‌سازی خطی استفاده می‌کند که همانی (Identity) است. بنابراین ورودی دریافت شده را بدون تغییر در خروجی برمی‌گرداند. بنابراین خواهیم داشت:

1    def fPropagate(self,
2                   X:np.ndarray) -> tuple:
3        Z1 = np.dot(X, self.W1) + self.B1
4        O1 = self.Activation(Z1)
5        Zo = np.dot(O1, self.Wo) + self.Bo
6        Oo = Zo
7        return O1, Oo

توجه داشته باشید که برای فرآیند آموزش مدل، نیاز به خروجی تمامی لایه‌ها داریم، بنابراین خروجی هر دو لایه را در خروجی برمی‌گردانیم. توجه داشته باشید که این متد در خروجی دو آرایه برمی‌گرداند که هر دو داخل یک تاپل (Tuple) قرار گرفته‌اند.

به این ترتیب این متد می‌تواند انتشار رو به جلو را انجام دهد.

متد پس انتشار خطا

پس از ایجاد مدل، نیاز داریم تا آن را بر روی مجموعه داده آموزش دهیم. به این منظور از «قانون دلتا» (Generalized Delta Rule | GDR) استفاده می‌کنیم. این روش خطای حاصل در خروجی شبکه را در عکس جهت انتشار می‌دهد. (Error Backpropagation) و به این وسیله میزان و جهت تغییرات هر پارامتر را محاسبه می‌کند. اگر بردار $$x$$ در ورودی شبکه وارد شود و خروجی هدف بردار $$y$$ باشد، برای یک پرسپترون تک لایه، خواهیم داشت:

$$\begin{aligned} &\Delta W_{i, j}=\eta \cdot x_i \cdot \omega_1\left(O_{1, j}\right) \cdot \delta_j \\ &\delta_j=\sum_{k=1}^{n Y} W_{j, k} \cdot\left(y_k-O_{o, k}\right) \\ &\Delta W_{j, k}=\eta \cdot O_{1, j} \cdot \omega_o\left(O_{o, k}\right) \cdot \delta_k \\ &\delta_k=y_k-O_{o, k} \end{aligned}$$

در این روابط $$\eta$$ نشان‌دهنده «نرخ یادگیری» (Learning Rate) است.

روابط فوق مقدار به‌روزرسانی هر وزن را نشان می‌دهد. توجه داشته باشید که فرم کلی عبارت مشابه یکدیگر است و از مفاهیم یکسانی استنباط شده‌اند.

شمارنده $$i$$ نشان‌دهنده‌ نورون شماره $$i$$ در لایه ورودی است. شمارنده‌های $$j$$ و $$k$$ نیز به ترتیب شماره نورون در لایه پنهان و لایه خروجی را نشان می‌دهند.

با توجه به اینکه ورودی بایاس‌ها همواره 1 است، مقادیر به‌روزرسانی آن‌ها نیز به شکل زیر است:

$$\begin{aligned} &\Delta B_j=\eta \cdot \omega_1\left(O_{1, j}\right) \cdot \delta_j \\ &\Delta B_k=\eta \cdot \omega_o\left(O_{o, k}\right) \cdot \delta_k \end{aligned}$$

به این ترتیب تمامی روابط مورد نیاز برای به‌روزرسانی پارامترها را داریم.

حال متد پس انتشار خطا را پیاده‌سازی می‌کنیم. در ورودی این متد دو بردار $$x$$ و $$y$$ را دریافت می‌کنیم:

1    def bPropagate(self,
2                   x:np.ndarray,
3                   y:np.ndarray):

حال با فراخوانی متد fPropagate خروجی هر لایه را محاسبه می‌کنیم:

1    def bPropagate(self,
2                   x:np.ndarray,
3                   y:np.ndarray):
4        O1, Oo = self.fPropagate(x)

حال روابط گفته شده را در 4 بخش پیاده‌سازی می‌کنیم:

1    def bPropagate(self,
2                   x:np.ndarray,
3                   y:np.ndarray):
4        O1, Oo = self.fPropagate(x)
5        # Hidden Layer Weight Update
6        for i in range(self.nX):
7            for j in range(self.nH):
8                dj = np.inner(self.Wo[j, :], (y - Oo))
9                self.W1[i, j] += self.lr * x[i] * self.dActivation(O1[j]) * dj
10        # Hidden Layer Bias Update
11        for j in range(self.nH):
12            dj = np.inner(self.Wo[j, :], (y - Oo))
13            self.B1[j] += self.lr * self.dActivation(O1[j]) * dj
14        # Output Layer Weight Update
15        for j in range(self.nH):
16            for k in range(self.nY):
17                dk = y[k] - Oo[k]
18                self.Wo[j, k] += self.lr * O1[j] * dk
19        # Output Layer Bias Update
20        for k in range(self.nY):
21            dk = y[k] - Oo[k]
22            self.Bo[k] += self.lr * dk

به این ترتیب این متد خواهد توانست با دریافت $$x$$ و $$y$$ متناظر با یکدیگر، پارامترهای شبکه را برای یک گام به‌روزرسانی کند.

توجه داشته باشید که عبارت $$\delta_i$$ که در کد با نام dj شناخته می‌شود را با استفاده از numpy.inner محاسبه می‌کنیم که همان عمل Summation موجود در فرمول را انجام می‌دهد.

فیلم آموزش رگرسیون خطی و شبکه عصبی MLP در پایتون برای پیش بینی چربی بدن (رایگان) در فرادرس

کلیک کنید

متد آموزش مدل

متد bPropagate تنها برای یک داده و یک مرحله مدل را آموزش می‌دهد. باید متد دیگری تعریف کنیم که با دریافت کل مجموعه داده، به دفعات مشخص مدل را آموزش دهد. این متد در ورودی مجموعه‌ای از بردارهای ورودی، مجموعه‌ای از بردارهای خروجی، تعداد مراحل آموزش مدل و نرخ یادگیری را دریافت خواهد کرد:

1    def Fit(self,
2            X:np.ndarray,
3            Y:np.ndarray,
4            nEpoch:int,
5            lr:float):

حال در اولین قدم، تعداد مراحل و نرخ یادگیری را در شی ذخیره می‌کنیم:

1    def Fit(self,
2            X:np.ndarray,
3            Y:np.ndarray,
4            nEpoch:int,
5            lr:float):
6        self.nEpoch = nEpoch
7        self.lr = lr

حال باید تعداد ورودی و تعداد خروجی شبکه را ذخیره کنیم:

1    def Fit(self,
2            X:np.ndarray,
3            Y:np.ndarray,
4            nEpoch:int,
5            lr:float):
6        self.nEpoch = nEpoch
7        self.lr = lr
8        self.nX = X.shape[1]
9        self.nY = Y.shape[1]

به این ترتیب ابعاد شبکه ذخیره خواهد شد.

در طول آموزش مدل، خطای مدل کاهش می‌یابد، به منظور نمایش این فرآیند در قالب یک نمودار، آرایه‌ای خالی برای ذخیره خطاها در انتهای هر مرحله ایجاد می‌کنیم:

1    def Fit(self,
2            X:np.ndarray,
3            Y:np.ndarray,
4            nEpoch:int,
5            lr:float):
6        self.nEpoch = nEpoch
7        self.lr = lr
8        self.nX = X.shape[1]
9        self.nY = Y.shape[1]
10        self.Log = np.zeros(nEpoch + 1)

با توجه به اینکه قصد داریم قبل از شروع آموزش مدل نیز خطای آن را ذخیره کنیم، طول آرایه به اندازه 1 واحد بیشتر از تعداد کل مراحل خواهد بود. حال مقداردهی اولیه وزن‌ها را انجام می‌دهیم:

1    def Fit(self,
2            X:np.ndarray,
3            Y:np.ndarray,
4            nEpoch:int,
5            lr:float):
6        self.nEpoch = nEpoch
7        self.lr = lr
8        self.nX = X.shape[1]
9        self.nY = Y.shape[1]
10        self.Log = np.zeros(nEpoch + 1)
11        self.InitializeParameters()

قبل از شروع آموزش مدل، یک بار پیشبینی مدل را دریافت می‌کنیم و خطای NRMSE یا Normalized Root Mean Squared Error را محاسبه می‌کنیم. این معیار به شکل زیر محاسبه می‌شود:

$$\begin{aligned} &\operatorname{NRMSE}(Y, \hat{Y})=100 \times \frac{R M S E(Y, \hat{Y})}{\max (Y)-\min (Y)}=100 \times \frac{\sqrt{M S E(Y, \hat{Y})}}{\max (Y)-\min (Y)}\\ &=100 \times \frac{\sqrt{\frac{1}{N} \sum_{i=1}^N\left(Y_i-\hat{Y}_i\right)^2}}{\max (Y)-\min (Y)} \end{aligned}$$

برای آشنایی با NRMSE و سایر معیارهای ارزیابی رگرسیون، می‌توانید به مطلب بررسی معیارهای ارزیابی رگرسیون در پایتون – پیاده سازی + کدها مراجعه کنید.

به این منظور خواهیم داشت:

1    def Fit(self,
2            X:np.ndarray,
3            Y:np.ndarray,
4            nEpoch:int,
5            lr:float):
6        self.nEpoch = nEpoch
7        self.lr = lr
8        self.nX = X.shape[1]
9        self.nY = Y.shape[1]
10        self.Log = np.zeros(nEpoch + 1)
11        self.InitializeParameters()
12        _, Oo = self.fPropagate(X)
13        MSE = np.mean((Y - Oo) ** 2)
14        RMSE = MSE ** 0.5
15        NRMSE = 100 * RMSE / (Y.max() - Y.min())

حال خطای حاصل را ذخیره می‌کنیم و آن را در خروجی نمایش می‌دهیم:

1    def Fit(self,
2            X:np.ndarray,
3            Y:np.ndarray,
4            nEpoch:int,
5            lr:float):
6        self.nEpoch = nEpoch
7        self.lr = lr
8        self.nX = X.shape[1]
9        self.nY = Y.shape[1]
10        self.Log = np.zeros(nEpoch + 1)
11        self.InitializeParameters()
12        _, Oo = self.fPropagate(X)
13        MSE = np.mean((Y - Oo) ** 2)
14        RMSE = MSE ** 0.5
15        NRMSE = 100 * RMSE / (Y.max() - Y.min())
16        self.Log[0] = NRMSE
17        print(f'Epoch: 0/{nEpoch} -- Loss: {NRMSE:.2f} %')

حال می‌توانیم حلقه مربوط به آموزش مدل را ایجاد کنیم. این حلقه به تعداد nEpoch تکرار خواهد شد:

1    def Fit(self,
2            X:np.ndarray,
3            Y:np.ndarray,
4            nEpoch:int,
5            lr:float):
6        self.nEpoch = nEpoch
7        self.lr = lr
8        self.nX = X.shape[1]
9        self.nY = Y.shape[1]
10        self.Log = np.zeros(nEpoch + 1)
11        self.InitializeParameters()
12        _, Oo = self.fPropagate(X)
13        MSE = np.mean((Y - Oo) ** 2)
14        RMSE = MSE ** 0.5
15        NRMSE = 100 * RMSE / (Y.max() - Y.min())
16        self.Log[0] = NRMSE
17        print(f'Epoch: 0/{nEpoch} -- Loss: {NRMSE:.2f} %')
18        for Epoch in range(1, nEpoch + 1):

در هر مرحله از آموزش، به ازای هر داده یک بار متد bPropagate را فرامی‌خوانیم:

1    def Fit(self,
2            X:np.ndarray,
3            Y:np.ndarray,
4            nEpoch:int,
5            lr:float):
6        self.nEpoch = nEpoch
7        self.lr = lr
8        self.nX = X.shape[1]
9        self.nY = Y.shape[1]
10        self.Log = np.zeros(nEpoch + 1)
11        self.InitializeParameters()
12        _, Oo = self.fPropagate(X)
13        MSE = np.mean((Y - Oo) ** 2)
14        RMSE = MSE ** 0.5
15        NRMSE = 100 * RMSE / (Y.max() - Y.min())
16        self.Log[0] = NRMSE
17        print(f'Epoch: 0/{nEpoch} -- Loss: {NRMSE:.2f} %')
18        for Epoch in range(1, nEpoch + 1):
19            for x, y in zip(X, Y):
20                self.bPropagate(x, y)

به این ترتیب آموزش مدل کامل خواهد شد. برای بررسی خطا در انتهای هر مرحله نیز بار دیگر NRMSE را محاسبه می‌کنیم:

1    def Fit(self,
2            X:np.ndarray,
3            Y:np.ndarray,
4            nEpoch:int,
5            lr:float):
6        self.nEpoch = nEpoch
7        self.lr = lr
8        self.nX = X.shape[1]
9        self.nY = Y.shape[1]
10        self.Log = np.zeros(nEpoch + 1)
11        self.InitializeParameters()
12        _, Oo = self.fPropagate(X)
13        MSE = np.mean((Y - Oo) ** 2)
14        RMSE = MSE ** 0.5
15        NRMSE = 100 * RMSE / (Y.max() - Y.min())
16        self.Log[0] = NRMSE
17        print(f'Epoch: 0/{nEpoch} -- Loss: {NRMSE:.2f} %')
18        for Epoch in range(1, nEpoch + 1):
19            for x, y in zip(X, Y):
20                self.bPropagate(x, y)
21            _, Oo = self.fPropagate(X)
22            MSE = np.mean((Y - Oo) ** 2)
23            RMSE = MSE ** 0.5
24            NRMSE = 100 * RMSE / (Y.max() - Y.min())
25            self.Log[Epoch] = NRMSE
26            print(f'Epoch: {Epoch}/{nEpoch} -- Loss: {NRMSE:.2f} %')

به این ترتیب مقادیر خطا در طول آموزش نمایش داده خواهد شد، همچنین در آرایه self.Log نیز ذخیره می‌شود.

متد پیش بینی

تا به اینجا توانستیم متدهای مورد نیاز برای ایجاد و آموزش مدل را پیاده‌سازی کنیم. متد دیگری نیز نیاز داریم تا پس از آموزش مدل، با وارد کردن مجموعه داده جدید، خروجی را برای آن مجموعه داده نیز داشته باشیم. این متد را با نام Predict می‌شناسیم و در ورودی آرایه X را دریفات خواهد کرد و در خروجی تنها خروجی نهایی مدل را برخواهد گرداند:

1    def Predict(self,
2                X:np.ndarray) -> np.ndarray:
3        _, Oo = self.fPropagate(X)
4        return Oo

توجه داشته باشید که متد fPtopagate نیز کار مشابهی را انجام می‌دهد اما به دلیل سهولت در استفاده کاربر، از این حالت استفاده می‌کنیم.

به این ترتیب تمامی متدهای مورد نیاز برای شبکه عصبی پیاده‌سازی شده و آماده استفاده هستند.

ایجاد مجموعه داده

برای بررسی عملکرد شبکه عصبی پیاده‌سازی شده، نیاز به یک مجموعه داده داریم. به این منظور ابتدا تنظیمات زیر را در ابتدای کد اعمال می‌کنیم:

1np.random.seed(0)
2plt.style.use('ggplot')

حال یک مجموعه داده مصنوعی (Synthetic Dataset) با ضابطه زیر ایجاد می‌کنیم:

$$y = sin (x)$$

برای ایجاد مقادیر $$X$$ را به صورت تصادفی از بازه $$[-\pi , +\pi]$$ انتخاب می‌کنیم:

1X = np.random.uniform(low=-np.pi,
2                      high=+np.pi,
3                      size=(100, 1))

مقادیر $$Y$$ نیز مطابق با ضابطه آورده شده، به شکل زیر محاسبه می‌شود:

1Y = np.sin(X)

حال می‌توانیم مجموعه داده ایجاد شده را نمایش دهیم. به این منظور از Scatter Plot موجود در کتابخانه Matplotlib استفاده می‌کنیم:

1plt.scatter(X,
2            Y,
3            s=12,
4            marker='o',
5            c='teal',
6            alpha=0.9)
7plt.title('Created Dataset Plot')
8plt.xlabel('X')
9plt.ylabel('Y')
10plt.show()

در خروجی کد فوق، نمودار زیر حاصل می‌شود:

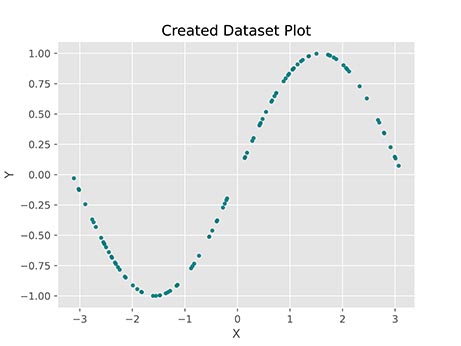
مشاهده می‌کنیم که نقاطی تصادفی از نمودار سینوسی انتخاب می‌شود.

ایجاد و آموزش مدل

حال می‌توانیم یک شی از کلاس نوشته شده ایجاد کنیم:

1Model = SLP(20, 'l-relu')

به این ترتیب یک پرسپترون تک لایه با 20 نورون ایجاد می‌شود. تابع فعال‌سازی این نورون‌ها Leaky-ReLU است.

حال می‌توانیم مدل را بر روی مجموعه داده ایجاد شده آموزش دهیم:

1Model.Fit(X, Y, 300, 1e-3)

به این ترتیب مدل با نرخ یادگیری برابر با 0.001 به تعداد 300 مرحله بر روی مجموعه آموزش می‌بیند.

پس از اجرای کد فوق، نتایج به شکل زیر نمایش داده می‌شود:

1Epoch: 0/300   -- Loss: 507.34 %
2Epoch: 1/300   -- Loss:  41.15 %
3Epoch: 2/300   -- Loss:  25.93 %
4...
5Epoch: 298/300 -- Loss:   3.26 %
6Epoch: 299/300 -- Loss:   3.25 %
7Epoch: 300/300 -- Loss:   3.24 %

به این ترتیب مشاهده می‌کنیم که مدل قبل از شروع آموزش و با وزن‌های تصادفی انتخاب شده، دارای خطای ۵۰۷ درصد بوده و تنها با یک مرحله آموزش توانسته این خطا را به ۴۱ درصد کاهش دهد. اغلب بهبود عملکرد مدل، برای گام‌های ابتدایی آموزش بیشتر است. در مراحل انتهایی، خطای مدل از ۳٫۲۶ درصد به ۳٫۲۴ درصد کاهش یافته است که نشان از همگرایی مدل و بهبودهای اندک دارد.

بررسی خطا در طول آموزش

در طول آموزش مدل، آرایه self.Log نیز کامل می‌شود. برای مشاهده این خطاها می‌توانیم کد زیر را بنویسیم:

1print(Model.Log)

در خروجی کد فوق یک آرایه به شکل زیر نمایش داده خواهد شد:

1[507.34458356  41.1541946   25.93488039  20.79921183  17.87710731
2  16.03121077  14.72792736  13.74237265  12.93760266  12.26774852
3  11.70816481  11.23009043  10.81068193  10.44370871  10.11500974
4   ...
5   3.36195324   3.35056463   3.339609     3.32618531   3.31366713
6   3.30170847   3.28764272   3.27423003   3.26142911   3.24794898
7   3.23527108]

به این ترتیب این آرایه نیز به درستی پر شده است. حال می‌توانیم نمودار این آرایه را رسم کنیم:

1T = np.arange(start=0,
2              stop=Model.nEpoch + 1,
3              step=1)
4plt.plot(T,
5         Model.Log,
6         ls='-',
7         lw=1.2,
8         c='teal')
9plt.title('Model Loss Over Training')
10plt.xlabel('Epoch')
11plt.ylabel('NRMSE (%)')
12plt.show()

توجه داشته باشید که آرایه T شامل شماره مراحل است و به دلیل اینکه اولین خطا مربوط به خطای قبل از آموزش است، بهتر است اولین مقدار این آرایه 0 باشد. پس از اجرای کد فوق، نمودار زیر حاصل می‌شود:

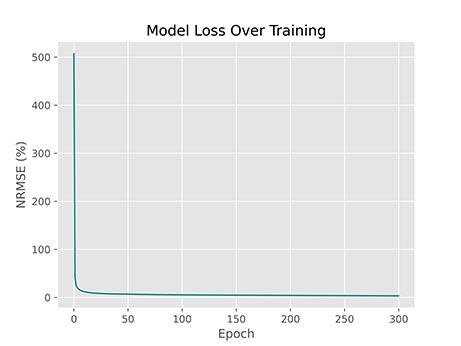
به این ترتیب نمودار حاصل می‌شود. اما این نمودار مشکلاتی دارد. برای مثال بهبود عملکرد از مرحله 10 به بعد چندان واضح مشاهده نمی‌شود. این مشکل حاصل از تغییرات شدید در مراحل اولیه آموزش است. می‌توان با لگاریتمی کردن مقیاس محور عمودی، این مشکل را رفع کرد. به این حالت، نمودار نیمه-لگاریتمی (Semi-Logarithm) گفته می‌شود. به این منظور از matplotlib.pyplot.yscale استفاده می‌کنیم:

1T = np.arange(start=0,
2              stop=Model.nEpoch + 1,
3              step=1)
4plt.plot(T,
5         Model.Log,
6         ls='-',
7         lw=1.2,
8         c='teal')
9plt.title('Model Loss Over Training')
10plt.xlabel('Epoch')
11plt.ylabel('NRMSE (%)')
12plt.yscale('log')
13plt.show()

حال پس از اجرای دوباره، نمودار به شکل زیر خواهد بود:

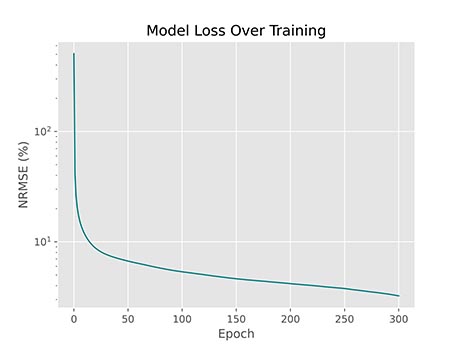
به این ترتیب مشاهده می‌کنیم که این نمودار بهبود خطا را بهتر نشان می‌دهد. در بازه بین مراحل 50 تا 250، یک خط صاف داریم. با توجه به اینکه محور افقی لگاریتمی است، می‌توان گفت سرعت بهبود برابر با لگاریتم است. در بازه مراحل 0 تا 50 نیز نمودار کاهشی شدیدتر از خط صاف دارد بنابراین می‌توان گفت در این بازه، سرعت بهبود مدل بیشتر از لگاریتم است.

رسم نمودار پیشبینی

می‌توانیم خروجی حاصل را در مقابل نمودار سینوسی رسم کنیم و شباهت این دو نمودار به یکدیگر را بررسی کنیم. به این منظور ابتدا 201 نقطه با فاصله یکسان در بازه $$[-\pi , +\pi]$$ انتخاب می‌کنیم و مقدار تابع سینوسی برای این نقاط را محاسبه می‌کنیم:

1X2 = np.linspace(start=-np.pi, stop=+np.pi, num=201).reshape(-1, 1)
2Y2 = np.sin(X2)

حال می‌توانیم با استفاده از متد Predict، پیشبینی‌های مدل برای این نقاط را نیز محاسبه کنیم:

1P2 = Model.Predict(X2)

در نهایت می‌توانیم نقاط داده، تابع سینوسی و پیشبینی مدل برای این تابع را رسم کنیم:

1plt.scatter(X,
2            Y,
3            s=20,
4            marker='o',
5            c='b',
6            label='Data')
7plt.plot(X2,
8         Y2,
9         ls='-',
10         lw=1.2,
11         c='k',
12         label='Target Function')
13plt.plot(X2,
14         P2,
15         ls='-',
16         lw=1.2,
17         c='crimson',
18         label='Model Prediction')
19plt.title('Model Prediction')
20plt.xlabel('X')
21plt.ylabel('Y')
22plt.legend()
23plt.show()

به این ترتیب دو منحنی و یک مجموعه نقطه در نمودار نهایی خواهیم داشت. پس از اجرای کد فوق، نمودار زیر حاصل می‌شود:

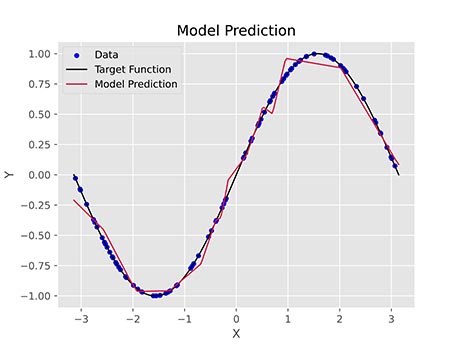
به این ترتیب مشاهده می‌کنیم که مدل توانست در اغلب موارد پیشبینی نزدیک به واقعیت داشته باشد. در برخی بازه‌ها نیز عملکرد مدل چندان خوب نبود است. با تنظیم هایپرپارامترهای (Hyperparameter) مدل و تغییر شرایط ابتدایی مسئله، می‌توان این مشکل را حل کرد.

اگر همین مدل را با 15 نورون، به تعداد 1000 مرحله با نرخ یادگیری 0.002 آموزش دهیم، خطای مدل به ۱٫۰۱ درصد کاهش می‌یابد و نمودار نهایی به شکل زیر خواهد بود:

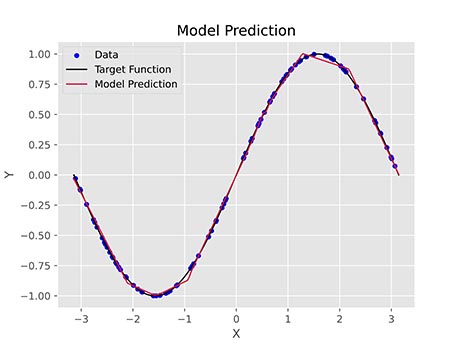
به این ترتیب مشاهده می‌کنیم که مدل به نتایج بهتری دست یافته است.

اگر همین مسئله را با 15 نورون ReLU به تعداد 1000 مرحله با نرخ یادگیری 0.002 آموزش دهیم، خطای نهایی ۱٫۹۱ درصد خواهد بود و نمودار زیر حاصل خواهد شد:

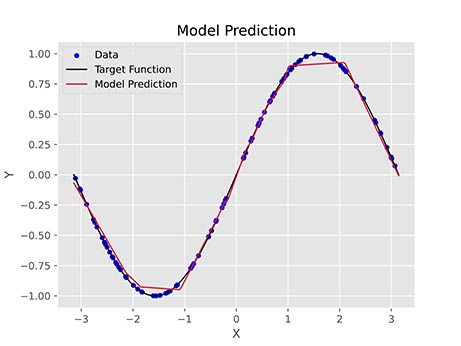
مشاهده می‌کنیم که در شرایطی یکسان، تابع فعال‌سازی ReLU عملکرد بدتری نسبت به Leaky ReLU داشته است که با توجه به توضیحات گفته شده، قابل توجیه است.

توجه داشته باشید که نرخ یادگیری هایپرپارامتر بسیار مهمی است و تنظیم آن در بسیاری از مسائل نیاز است. مقدار کم آن باعث می‌شود مدل نتواند به نقاط بهینه بهتر دست یابد. مقادیر بالای آن نیز باعث می‌شود مدل واگرا (Diverge) شود که هر دو مورد از این حالات مناسب نیست. برای مثال شکل زیر خطای مدلی با 15 نورون Leaky ReLU است که با نرخ یادگیری 0.03824 آموزش دیده است:

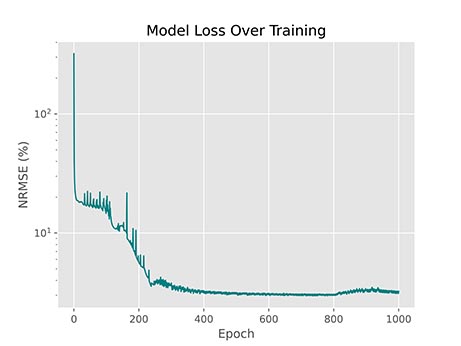
مشاهده می‌کنیم که روند آموزش این مدل پرنوسان بوده و دارای ثبات نیست.

به این منظور بهتر است نرخ یادگیری در ابتدای یادگیری مدل از یک مقدار بزرگ شروع شود و در طول مراحل آموزش مقدار آن کاهش یابد.

به این ترتیب آموزش مدل و تاثیر پارامترهای مختلف را بر روی آن مشاهده کردیم.

آموزش مدل با ورودی و خروجی‌های دارای ابعاد بالاتر

مجموعه داده ایجاد شده، دارای تنها یک ورودی و یک خروجی بود. کد نوشته شده قابلیت پشتیبانی از چندین ورودی و چندین خروجی را دارد. به این منظور در کد دیگری، مجموعه داده جدیدی با ضوابط زیر تولید می‌کنیم:

$$\begin{aligned} &y_1=\frac{x_1 \times x_2}{8} \\ &y_2=\frac{-x_1+x_2+1.2 \times x_3}{7.5} \end{aligned}$$

به این ترتیب سه ورودی و دو خروجی خواهیم داشت. 300 داده به این ضوابط تولید می‌کنیم:

1X = np.random.uniform(low=-np.pi,
2                      high=+np.pi,
3                      size=(300, 3))
4
5Y = np.zeros((300, 2))
6
7Y[:, 0] = X[:, 0] * X[:, 1] / 8
8Y[:, 1] = (-X[:, 0] +  X[:, 1] + 1.2 * X[:, 2]) / 7.5

حال می‌توانیم نمودار این مجموعه داده را رسم کنیم. با توجه به اینکه 3 متغیر مستقل و 2 متغیر وابسته داریم، 6 نمودار قابل رسم خواهد بود:

1k = 1
2
3for i in range(Y.shape[1]):
4    for j in range(X.shape[1]):
5        plt.subplot(2, 3, k)
6        plt.scatter(X[:, j],
7                    Y[:, i],
8                    s=12,
9                    marker='o',
10                    c='teal',
11                    alpha=0.9)
12        if i == Y.shape[1] - 1:
13            plt.xlabel(f'X{j + 1}', fontdict={'color':'crimson'})
14        if j == 0:
15            plt.ylabel(f'Y{i + 1}', fontdict={'color':'crimson'})
16        k += 1
17
18plt.tight_layout()
19plt.show()

پس از اجرای این کد، نمودار زیر حاصل خواهد شد:

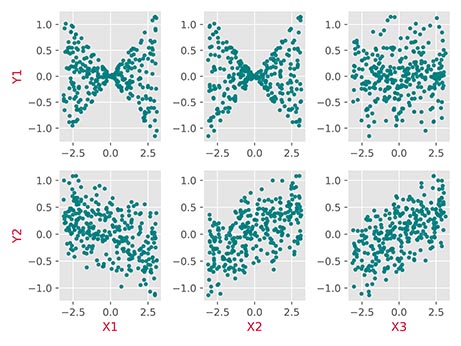
به این ترتیب توزیع داده‌ها و همبستگی بین آن‌ها مشخص می‌شود.

حال یک شبکه عصبی ایجاد می‌کنیم و آن را آموزش می‌دهیم:

1Model = SLP(40, 'l-relu')
2Model.Fit(X, Y, 300, 1e-3)

در اجرای کد فوق، خطای برگردانده می‌شود. این خطا به دلیل روش محاسبه NRMSE است. با توجه به اینکه در کد قبلی تنها یک خروجی داشتیم، مقدار NRMSE نیز یک عدد بود اما با افزایش تعداد خروجی‌های مدل، باید به یک بردار تبدیل شود، به همین دلیل، کد مربوط به متد Fit را به شکل زیر تغییر می‌دهیم:

1    def Fit(self,
2            X:np.ndarray,
3            Y:np.ndarray,
4            nEpoch:int,
5            lr:float):
6        self.nEpoch = nEpoch
7        self.lr = lr
8        self.nX = X.shape[1]
9        self.nY = Y.shape[1]
10        self.Log = np.zeros((nEpoch + 1, self.nY))
11        self.InitializeParameters()
12        _, Oo = self.fPropagate(X)
13        MSE = np.mean((Y - Oo) ** 2, axis=0)
14        RMSE = MSE ** 0.5
15        NRMSE = 100 * RMSE / (Y.max(axis=0) - Y.min(axis=0))
16        self.Log[0, :] = NRMSE
17        print(f'Epoch: 0/{nEpoch} -- Loss: {np.round(NRMSE, 2)} %')
18        for Epoch in range(1, nEpoch + 1):
19            for x, y in zip(X, Y):
20                self.bPropagate(x, y)
21            _, Oo = self.fPropagate(X)
22            MSE = np.mean((Y - Oo) ** 2, axis=0)
23            RMSE = MSE ** 0.5
24            NRMSE = 100 * RMSE / (Y.max(axis=0) - Y.min(axis=0))
25            self.Log[Epoch, :] = NRMSE
26            print(f'Epoch: {Epoch}/{nEpoch} -- Loss: {np.round(NRMSE, 2)} %')

نکاتی از کد که باید توجه شود:

1. با توجه به اینکه به تعداد self.ny خروجی وجود دارد، آرایه self.Log را به شکل دوبعدی با ابعاد تعریف می‌کنیم.
2. ماتریس خطا و ماتریس مربعات خطا دو بعدی است. برای میانگین‌گیری از این ماتریس، از تابع mean استفاده می‌کنیم، اما این عملیات باید برای هر خروجی یا ستون جداگانه انجام شود. به همین دلیل ورودی axis=0 را برای این تابع در نظر می‌گیریم.
3. برای محاسبه NRMSE باید RMSE بر Range متغیر هدف تقسیم شود. این فاصله برابر با اختلاف بزرگ‌ترین و کوچک‌ترین مقدار است. به همین دلیل متدهای min و max استفاده شود. اما به دلیل اینکه ماتریس Y دارای بیشتر از 1 ستون است، باید برای این متد نیز ورودی axis=0 تعیین شود.
4. در انتهای هر مرحله نیز مقدار خطا نمایش داده شد. با توجه به اینکه مقدار NRMSE آرایه است، باید از تابع numpy.round برای گرد کردن مقادیر استفاده کنیم.

با تغییر کد و اجرای دوباره، خطا رفع شده و به درستی اجرا می‌شود.

حال می‌توانیم نمودار خطا را برای هر دو خروجی به صورت جداگانه رسم کنیم:

1T = np.arange(start=0,
2              stop=Model.nEpoch + 1,
3              step=1)
4
5for i in range(Model.nY):
6    plt.subplot(1, 2, i + 1)
7    plt.plot(T,
8             Model.Log[:, i],
9             ls='-',
10             lw=1.2,
11             c='teal')
12    plt.xlabel('Epoch')
13    plt.ylabel(f'NRMSE of Y{i + 1} (%)')
14    plt.yscale('log')
15
16plt.tight_layout()
17plt.show()

در خروجی این کد، نمودار زیر حاصل می‌شود:

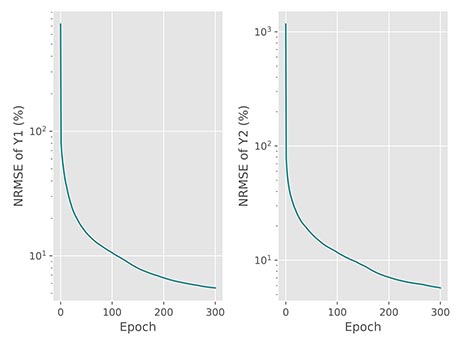
به این ترتیب مشاهده می‌کنیم که برای هر خروجی یک نمودار ایجاد شده است و هر دو نمودار نزولی است. مدل در انتهای آموزش، برای هر دو خروجی خطایی نزدیک به ۵٫۵ درصد دارد که مقدار مناسبی است. برای مدل‌هایی با خروجی‌های بیشتر، می‌توان میانگین NRMSE ها را بررسی کرد.

برای رسم عملکرد مدل نیز می‌توانیم دو نمودار دیگر رسم کنم. به این منظور از Scatter Plot استفاده می‌کنیم و مقادیر پیشبینی را در مقابل مقادیر واقعی نمایش می‌دهیم:

1P = Model.Predict(X)
2
3for i in range(Model.nY):
4    plt.subplot(1, 2, i + 1)
5    a = min(Y[:, i].min(), P[:, i].min()) - 0.2
6    b = max(Y[:, i].max(), P[:, i].max()) + 0.2
7    ab = np.array([a, b])
8    plt.scatter(Y[:, i], P[:, i], s=12, marker='o', c='teal', label='Data')
9    plt.plot(ab, ab, ls='-', lw=1.2, c='k', label='Y = X')
10    plt.title(f'Model Regression Plot of Y{i + 1}', fontdict={'size':10})
11    plt.xlabel('Target Values')
12    if i == 0:
13        plt.ylabel('Predicted Values')
14    plt.legend()
15
16plt.show()

در خروجی این کد نمودار زیر حاصل می‌شود:

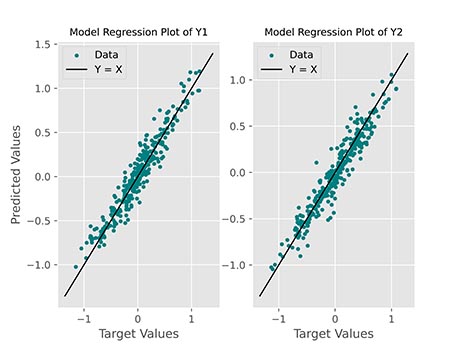
مشاهده می‌کنیم که برای هر دو خروجی، مقادیر به خوبی در اطراف خط $$Y = X$$ قرار گرفته‌اند.

می‌توان مقادیر $$R^{2}$$ یا ضریب تعیین را نیز محاسبه و در این نمودار نمایش داد:

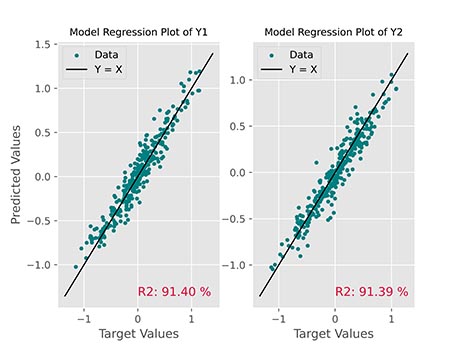
به این ترتیب نمودار اطلاعات جامع‌تری در رابطه با عملکرد مدل انتقال خواهد داد. برای رسم نمودار فوق، از کد زیر استفاده شده است:

1P = Model.Predict(X)
2
3for i in range(Model.nY):
4    MSE = np.mean((Y[:, i] - P[:, i]) ** 2)
5    R2 = 100 * (1 - MSE / Y[:, i].var())
6    plt.subplot(1, 2, i + 1)
7    a = min(Y[:, i].min(), P[:, i].min()) - 0.2
8    b = max(Y[:, i].max(), P[:, i].max()) + 0.2
9    ab = np.array([a, b])
10    plt.scatter(Y[:, i], P[:, i], s=12, marker='o', c='teal', label='Data')
11    plt.plot(ab, ab, ls='-', lw=1.2, c='k', label='Y = X')
12    plt.text(0, a, f'R2: {R2:.2f} %', fontdict={'size':12, 'color':'crimson'})
13    plt.title(f'Model Regression Plot of Y{i + 1}', fontdict={'size':10})
14    plt.xlabel('Target Values')
15    if i == 0:
16        plt.ylabel('Predicted Values')
17    plt.legend()
18
19plt.show()

برای محاسب امتیاز $$R^{2}$$ از رابطه زیر استفاده شده است:

$$R^2=1-\frac{\sum_{i=1}^n\left(Y_i-\widehat{Y}_i\right)^2}{\sum_{i=1}^n\left(Y_i-\bar{Y}\right)^2}=1-\frac{M S E(Y, \hat{Y})}{\text { Variance }(Y)}$$

پارامترهای‌های نهایی در پیاده سازی شبکه عصبی پرسپترون یک لایه در پایتون

در انتهای آموزش مدل، می‌توان پارامترهای نهایی را نیز مورد بررسی قرار داد، با کد زیر می‌توانیم تعداد و ابعاد هر مجموعه پارامتر را بررسی کرد:

1print(Model.W1.shape)
2print(Model.B1.shape)
3print(Model.Wo.shape)
4print(Model.Bo.shape)

در خروجی کد فوق نتایج زیر را خواهیم داشت:

1(3, 40)
2(40,)
3(40, 2)
4(2,)

به این ترتیب مشاهده می‌کنیم که بایاس‌ها دارای یک بُعد و وزن‌ها دارای  دو بُعد هستند. عدد 3 موجود در ابعاد از 3 ورودی شبکه، مقدار 2 از 2 خروجی شبکه و مقدار 40 نیز از 40 نورون لایه مخفی نشأت می‌گیرد.

مصورسازی وزن‌ها در پیاده سازی شبکه عصبی پرسپترون یک لایه در پایتون

می‌توان مقادیر وزن‌ها را نیز به شکل نمودار هسیتوگرام (Histogram) نمایش داد. به این منظور تعداد داده را به 500 افزایش می‌دهیم، سپس یک شبکه عصبی با 60 نورون Leaky ReLU ایجاد می‌کنیم و آن را 1000 مرحله با نرخ یادگیری 0.0002 آموزش می‌دهیم. سپس کد زیر را اجرا می‌کنیم:

1Parameters = np.hstack((Model.W1.ravel(),
2                        Model.B1,
3                        Model.Wo.ravel(),
4                        Model.Bo))
5
6plt.hist(Parameters, bins=17, color='crimson', alpha=0.8)
7plt.title('All Parameters Histogram Plot')
8plt.xlabel('Weight')
9plt.ylabel('Count')
10plt.show()

توجه داشته باشید که آرایه Parameters شامل تمامی پارامترها است. در نتیجه اجرای کد فوق، نمودار زیر حاصل می‌شود:

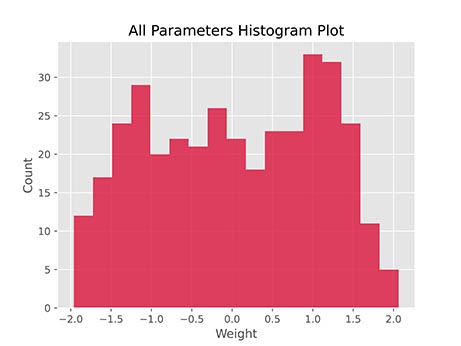
به این ترتیب مشاهده می‌کنیم که توزیع مقادیر با توزیع یکنواخت متفاوت است، بنابراین می‌توان از این اطلاعات برای مقداردهی اولیه وزن‌ها نیز استفاده کرد. این نمودار قبل از شروع آموزش مدل، به شکل زیر بوده است:

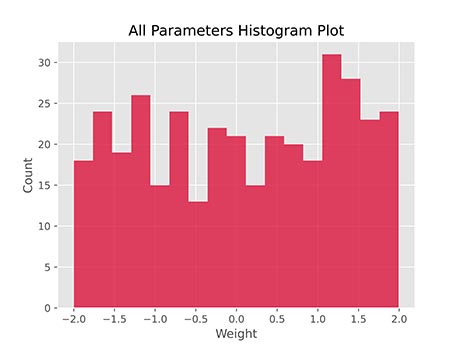
بنابراین می‌توان به این نتیجه رسید که این تغییر در توزیع معنادار است.

فیلم آموزش محاسبات عددی در پایتون Python در فرادرس

کلیک کنید

جمع‌بندی پیاده سازی شبکه عصبی پرسپترون یک لایه در پایتون

به این ترتیب پیاده‌سازی شبکه عصبی پرسپترون تک لایه به اتمام می‌رسد. برای مطالعه بیشتر می‌توان موارد زیر را بررسی کرد:

1. چگونه می‌توان تعداد نورون بهینه را پیدا کرد؟
2. چگونه می‌توان از بیش‌برازش (Overfitting) مدل پیاده‌سازی شده مطلع شد؟
3. اگر به جای استفاده از توزیع یکنواخت برای مقداردهی اولیه وزن‌ها، از توزیع نرمال (Normal Distribution) استفاده کنیم، سرعت همگرایی و نتایج چگونه تغییر خواهد کرد؟
4. تابع سیگموئید (Sigmoid) را نیز به توابع فعال‌سازی کلاس ایجاد شده اضافه کنید. تابع برای این تابع به چه شکل خواهد بود؟
5. اگر بخواهیم پرسپترون دو لایه (Double Layer Perceptron) پیاده‌سازی کنیم، معادلات به‌روزرسانی وزن‌ها به چه شکل خواهد بود؟
6. قانون دلتا (Delta Rule) چیست؟ این قانون چه مفهومی را نشان می‌دهد؟
7. اگر بخواهیم کد نوشته شده را برای طبقه‌بندی استفاده کنیم، چه تغییراتی باید در آن اعمال کنیم؟
8. حلقه‌های نوشته شده در متد bPropagate را با استفاده از محاسبات برداری ساده‌تر کنید. این فرآیند هزینه محاسباتی را تا چه اندازه کاهش می‌دهد؟
9. در کتابخانه‌های آماده برای یادگیری عمیق، از مفهومی به نام Batch برای هر بار به‌روزرسانی وزن‌ها استفاده می‌شود. این مفهوم چه مزیتی دارد؟
10. برای مجموعه داده ابتدایی، در طول آموزش مدل، برای هر مرحله نمودار رگرسیون را رسم و ذخیره کنید. با ایجاد GIF روند بهبود عملکرد مدل را نمایش دهید.