نمای لیاپانوف (Lyapunov Exponent) چیست؟ – از صفر تا صد

در این مطلب قصد داریم به معرفی یک معیار تحلیلی بسیار مفید بپردازیم که می‌تواند در توصیف کردن آشوب (Chaos) به ما کمک کند. این معیار «نمای لیاپانوف» (Lyapunov Exponent) یا توان لیاپانوف نام دارد. نمای لیاپانوف مشخص می‌کند که یک فاصله بسیار کوچک بین دو حالت که در ابتدا بسته بوده‌اند، با چه سرعتی در طول زمان رشد می‌کند. برای این کار از فرمول زیر استفاده می‌شود:

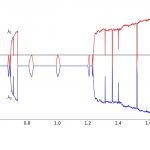
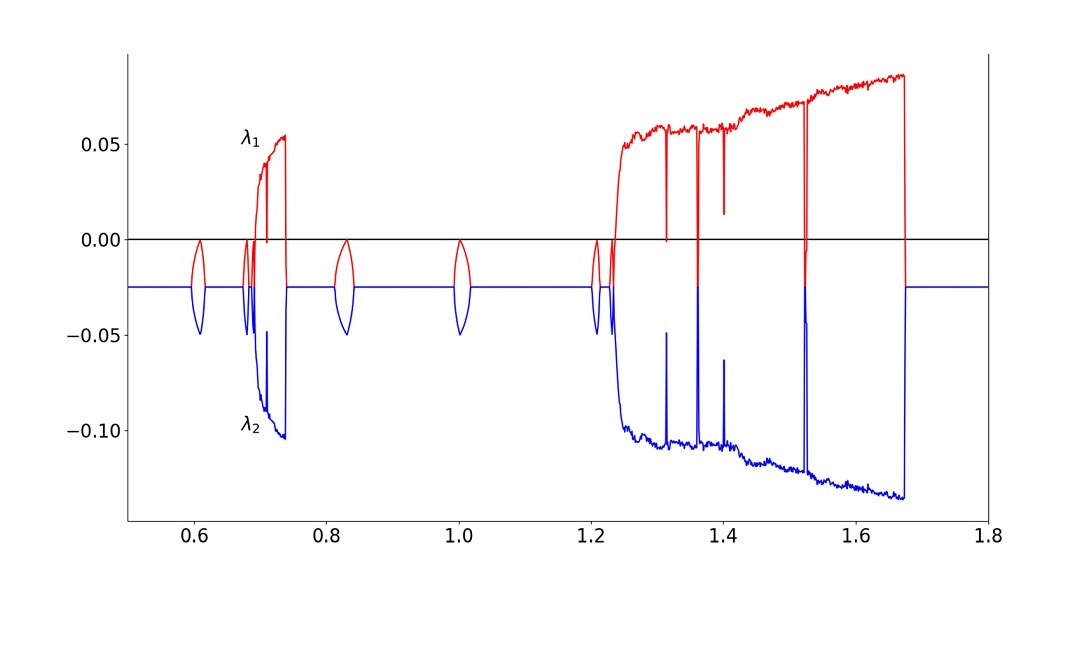
$$ F ^ { t } ( x _ 0 + ε ) − F ^ { t } ( x _ 0 ) ≈ ε e ^ { λ t } \label { 9 . 2 } $$

سمت چپ از این معادله برابر با فاصله بین دو مجموعه در ابتدا بسته، بعد از t گام است و سمت راست از معادله نشان دهنده این فرض است که فاصله در طول زمان به صورت نمایی رشد می‌کند. مقدار توان $$λ$$ در یک بازه طولانی زمانی (در حالت ایده‌آل $$t → ∞$$) اندازه‌گیری می‌شود و همان توان لیاپانوف است.

اگر مقدار $$λ > 0$$ باشد، آن‌گاه فواصل کوچک به صورت نامحدود در طول زمان رشد می‌کنند که این امر بدین معنی است که «مکانیزم کشش» (Stretching Mechanism) تاثیرگذار است. همچنین اگر $$λ < 0$$ باشد، فواصل کوچک به صورت نامحدود رشد نمی‌کنند. به عبارت دیگر، سیستم به تدریج در یک مسیر متناوب مستقر خواهد شد.

البته باید به این نکته توجه کرد که نمای لیاپانوف فقط کشش سیستم را توصیف می‌کند، اما کشش تنها مکانیزم یک سیستم آشوب نیست. بنابراین نتیجه می‌گیریم که مکانیزم «پیچش» (Folding) در توان لیاپانوف مد نظر قرار داده نشده است.

محاسبه نمای لیاپانوف

حال می‌توانیم با استفاده از ساده‌سازی‌های ریاضی، از معادله تبدیل فوق، یک معادله به دست بیاوریم که محاسبه آن راحت‌تر باشد. در نتیجه به صورت زیر عمل می‌کنیم:

$$ e ^ { λ t } ≈ \frac { | F ^ { t } ( x _ { 0 } + ε ) − F ^ { t } ( x _ { 0 } ) | } { ε } \label { 9 . 3 } $$

$$λ = \lim _ { t → ∞ , ε → 0 } \frac { 1 } { t } \log { \frac { | F ^ { t } ( x _ { 0 } + \varepsilon ) - F ^ { t } ( x _ { 0 } ) | } { \varepsilon } }$$

$$= \lim _ { t → ∞ 1 , ε → 0 } \frac { 1 } { t } \log { | \frac { d F } { d x } | _ { x = x _ 0 } | }$$

حال می‌توانیم قاعده مشتق زنجیره ای را به فرمول فوق اعمال کنیم:

$$λ = \lim _ { t → ∞ } \frac { 1 } { t } \log { | \frac { d F } { d x } } | _ { x = F ^ { t − 1 } ( x _ 0 ) = x _ { t − 1 } } · \frac{ d F } { d x } | _ { x = F ^ { t − 2 } ( x _ 0 ) = x _ { t − 2 } } · · · · \frac { d F } { d x } | _ { x = x _ { 0 } }$$

$$\lim _ { t \rightarrow \infty } \frac { 1 } { t } \sum ^ { t - 1 } _ { i = 0 } \log { | \frac { d F } { d x } | _ { x = x _ { i } } | }$$

نتیجه نهایی بسیار ساده است. نمای لیاپانوف به صورت یک میانگین زمانی از $$\log | \frac { d F } { d x } |$$ در هر گام از شبیه سازی سیستم محاسبه می‌شود. به دست آوردن توان لیاپانوف به این روش بسیار ساده است.

محاسبه توان لیاپانوف در پایتون

حال به سراغ پایتون می‌رویم.

فیلم آموزش طراحی سیستم های کنترل غیر خطی در فرادرس

کلیک کنید

کدهای مربوط به محاسبه نمای لیاپانوف در پایتون به صورت زیر است.

مثال

در این قسمت به عنوان مثال، توان لیاپانوف برای معادله زیر در طول تغییرات $$r$$ را با استفاده از کد پایتون فوق محاسبه می‌کنیم.

بنابراین داریم:

$$x _ { t } = x _ { t - 1 } + r - x ^ { 2 } _ { t - 1 }$$

نمودار حاصل از اجرای کد به صورت زیر خواهد بود.

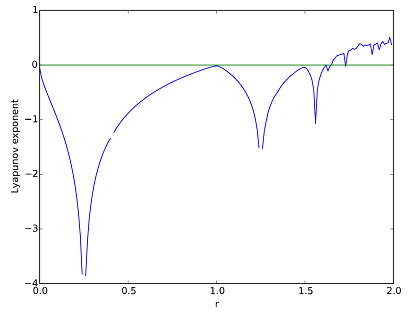$$x _ { t } = x _ { t - 1 } + r - x ^ { 2 } _ { t - 1 }$$" width="408" height="312">

با مقایسه این تصویر با «دیاگرام دوشاخگی» (Bifurcation Diagram) سیستم، که در زیر رسم شده است، می‌توان به این نتیجه رسید که بازه‌ای که در آن پارامتر توان لیاپانوف دارای مقادیر مثبت است، تا حد زیادی بر بازه‌ای که سیستم رفتار آشوبناک از خود نشان می‌دهد، منطبق است.

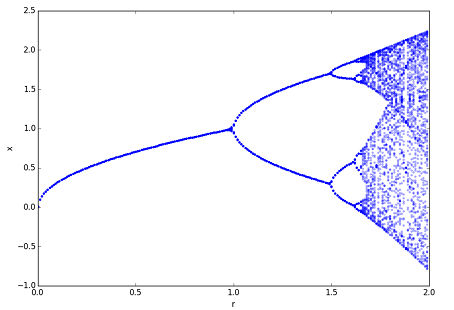$$x _ { t } = x _ { t - 1 } + r - x ^ { 2 } _ { t - 1 }$$" width="454" height="310">

همچنین، در هر زمانی که دوشاخگی اتفاق افتاده باشد، مثلا در $$r = 1 , 1 . 5$$، نمای لیاپانوف خط $$λ = 0$$ را لمس می‌کند که این نشان دهنده بحرانی بودن آن مقدار پارامتر است. در نهایت، مشاهده می‌شود که نقاط زیادی در نمودار وجود دارند که توان نمایی به منفی بی‌نهایت همگرا شده است. این مقادیر زمانی اتفاق می‌افتند که سیستم برای یک t مشخص با $$\frac { d F ^ { t } } { d x } _ { | x = x _ { 0 } } ≈ 0$$ به یک نقطه تعادل بسیار پایدار همگرا شود. به دلیل اینکه تعریف نمای لیاپانوف شامل لگاریتم این مشتق است، در نتیجه اگر صفر شود، توان لیاپانوف به سمت منفی بی‌نهایت همگرا می‌شود.

اگر این مطلب برای شما مفید بوده است، آموزش‌های زیر نیز به شما پیشنهاد می‌شوند:

• مجموعه آموزش‌های مهندسی کنترل
• آموزش طراحی سیستم های کنترل غیر خطی
• مجموعه آموزش‌های مهندسی برق
• سیستم غیر خطی — راهنمای جامع
• خطی سازی سیستم های غیر خطی — از صفر تا صد
• نقاط تعادل سیستم خطی — راهنمای جامع

^^