مدولاسیون دلتا (Delta) — راهنمای جامع

در مطالب قبلی مجله فرادرس به بررسی موضوع نمونه برداری در پردازش سیگنال پرداختیم و بیان کردیم که برای محقق شدن یک نمونه برداری مناسب، نرخ نمونهبرداری از یک سیگنال باید بزرگتر از «نرخ نایکویست» (Nyquist Rate) باشد. همچنین با روشهای مختلف مدولاسیون آنالوگ دامنه، فاز و فرکانس آشنا شدیم. در این مطلب قصد داریم به بررسی یکی دیگر از روشهای مدولاسیون دیجیتال بپردازیم که «مدولاسیون دلتا» (Delta Modulation) نام دارد.
مدولاسیون دلتا چیست؟
اگر بازه نمونه برداری در مدولاسیون کد پالس یا PCM به صورت قابل توجهی کاهش یابد، آنگاه اختلاف دامنه یک نمونه تا نمونه دیگر بسیار کوچک خواهد شد. در حالتی که اختلاف دامنه یک نمونه تا نمونه دیگر برابر با یک بیت کوانتیزاسیون باشد، آنگاه طول هر گام بسیار کوچک است و با نماد نمایش داده میشود.
بنابراین مدولاسیون دلتا به نوعی از تکنیکهای مدولاسیون دیجیتال اطلاق میشود که نرخ نمونه برداری بسیار بزرگتری دارند و در آنها طول گام بعد از کوانتیزاسیون مقادیر بسیار کوچکتری است که با نماد مشخص میشود. مدولاسیون دلتا داری ویژگیهای خاص خود است که در ادامه به چند مورد از آنها اشاره میکنیم:
- برای استفاده کامل از «همبستگی» (Correlation) سیگنال، یک ورودی «بیش نمونه برداری شده» (Over Sampled) به کار گرفته میشود.
- طراحی کوانتیزاسیون در این مدولاسیون بسیار ساده است.
- سرعت دنباله ورودی در مدولاسیون دلتا بسیار بزرگتر از نرخ نایکویست است.
- کیفیت عملکرد این روش مدولاسیون متوسط است.
- طراحی مدولاتور و دمدولاتور دلتا ساده است.
- یکی دیگر از ویژگیهای مدولاسیون دلتا، «تقریب پلهای» (Stair-Case Approximation) شکل موج خروجی آن است.
- طول گام در مدولاسیون دلتا بسیار کوچک و برابر با است.
- «نرخ بیت» (Bit Rate) را کاربر میتوان به دلخواه انتخاب کند.
- پیادهسازی مدولاسیون دلتا ساده است.
مدولاتور دلتا (Delta Modulator)
مدولاتور دلتا در واقع از یک «کوانتیزر» (Quantizer) یک بیتی و یک «مدار تاخیر» (Delay Circuit) همراه با دو مدار جمع کننده تشکیل شده است. در تصویر زیر بلوک دیاگرام یک مدولاتور دلتا نشان داده شده است.
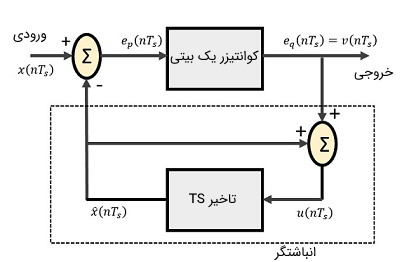
در مدار مدولاسیون کد پالس تفاضلی یا DPCM یک «پیشگو» (Predictor) وجود دارد که این واحد در مدولاتور دلتا با یک مدار تاخیر ساده جایگزین میشود. با توجه به دیاگرام فوق، سیگنالهای مختلف به صورت زیر هستند:
- : ورودی بیش نمونه برداری شده.
- : خروجی مدار جمع کننده و ورودی مدار کوانتیزر.
- : خروجی کوانتیزر که با برابر است.
- : خروجی مدار تاخیر.
- : ورودی مدار تاخیر.
حال با استفاده از نمادهای فوق، تلاش میکنیم که در ادامه به فرایند عملکرد مدولاسیون دلتا پی ببریم. با توجه به بلوک دیاگرام فوق، رابطه زیر صحیح است:
همچنین رابطه زیر در مورد این مدار صادق است:
همان طور که گفتیم، در روابط فوق، نشان دهنده مقدار قبلی مدار تاخیر و نشان دهنده خروجی کوانتیزر است که با برابر است. در نتیجه میتوان نوشت:
این رابطه بدین معنی است که ورودی کنونی واحد تاخیر با مجموع خروجی پیشین واحد کنترل و خروجی کنونی واحد کوانتیزر برابر است. حال با فرض شرایط اولیه صفر برای «انباشتگر» (Accumulator)، داریم:
حال باید به این نکته توجه کرد که:
خروجی واحد تاخیر در واقع خروجی یک انباشتگر است که به اندازه یک نمونه تاخیر داده شده است. با استفاده از معادلات شماره ۵ و ۶، در واقع میتوانیم یک ساختار کلی را برای دمدولاتور دلتا به دست آوریم. میتوان گفت خروجی مدار مدولاتور دلتا یک شکل موج تقریبی پلهای است که طول گام آن برابر با است. کیفیت خروجی شکل موج در حد متوسط است.
دمدولاتور دلتا
«دمدولاتور دلتا» (Delta Demodulator) از یک فیلتر پایین گذر، یک مدار جمع کننده و یک مدار تاخیر تشکیل شده است. مدار پیشگو که در مدولاتور دلتا وجود داشت، در دمدولاتور دلتا حذف میشود و به همین دلیل هیچ ورودی پیش فرضی به دمدولاتور داده نمیشود. در تصویر زیر نمایی از بلوک دیاگرام یک مدار دمدولاتور دلتا نشان داده شده است.
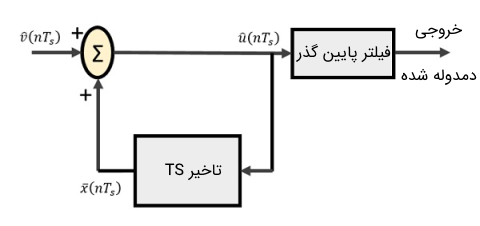
با توجه به دیاگرام فوق، سیگنالها به صورت زیر هستند:
- : برابر با نمونههای ورودی در نظر گرفته میشود.
- : خروجی مدار جمع کننده است.
- : برابر با خروجی تاخیر یافته است.
ابتدا یک رشته باینری به عنوان ورودی به مدار دمدولاتور دلتا وارد میشود. سپس خروجی تقریبی پلهای به یک فیلتر پایین گذر اعمال میشود. فیلترهای پایین گذر در کاربردهای مختلفی مورد استفاده قرار میگیرند. اما مهمترین دلیل برای استفاده از فیلتر پایین گذر در این مدار، حذف نویز در سیگنالهای خارج از باند است. خطای طول گامی که ممکن است در گیرنده اتفاق بیفتد را «نویز دانهای» (Granular Noise) میگویند که در اینجا با استفاده از فیلتر پایین گذر آن ها را حذف میکنیم. اگر هیچ نویزی وجود نداشته باشد، آنگاه خروجی مدولاتور برابر با ورودی دمدولاتور است.
مدولاسیون دلتا نسبت به مدولاسیون کد پالس تفاضلی یا DPCM مزایایی دارد که عبارت است از:
- کوانتیزر یک بیتی.
- طراحی بسیار ساده مدولاتور و دمدولاتور.
البته مدولاسیون دلتا دو عیب اساسی نیز دارد. اولا، زمانی که کوچک باشد، اعوجاج شیب به بار وجود دارد و دوما، زمانی که بزرگ باشد، در این مدولاسیون نویز دانهای حضور خواهد داشت.
مدولاسیون دلتا تطبیقی
در مدولاسیون دیجیتال به یک مسئله مهم برخورد میکنیم. مشکل اساسی در این مدولاسیون، تعیین طول گام است که روی کیفیت سیگنال خروجی تاثیر میگذارد. در شیبهای تند سیگنال مدوله کننده، به یک طول گام بزرگتر نیاز داریم، اما زمانی که شیب سیگنال پیام کندتر باشد، طول گام کوچکتری مورد نیاز است. معمولا جزئیات بسیار کوچک در گیرنده از دست میروند. بنابراین اگر بتوانیم تنظیمات طول گام را متناسب با نیاز کنترل کنیم، مدولاسیون موثرتری در نهایت به دست خواهد آمد.
کنترل کردن تنظیمات طول گام به این منظور انجام میشود که نمونه برداری به طریق دلخواه انجام گیرد. این مفهوم را «مدولاسیون دلتا تطبیقی» (Adaptive Delta Modulation) یا ADM میگویند. در تصویر زیر بلوک دیاگرم یک مدار مدولاتور دلتا تطبیقی نشان داده شده است.
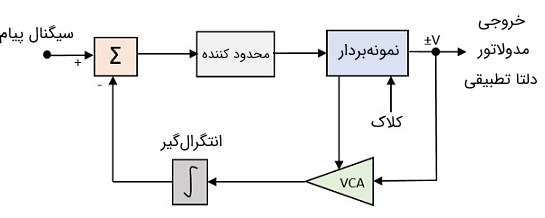
بهره «تقویت کننده کنترل شده با ولتاژ» (Voltage Controlled Amplifier) یا VCA توسط سیگنال خروجی از مدار نمونه بردار تنظیم میشود. بهره تقویت کننده میتواند طول گام را تنظیم کند و هر دو با هم متناسب هستند. مدولاسیون دلتا تطبیقی یا ADM میتواند اختلاف بین مقدار نمونه فعلی و مقدار پیشبینی شده برای نمونه بعدی را کوانتیزه کند. برای این کار مدولاتور از طول گامهای متغیر برای پیشبینی مقادیر بعدی استفاده میکند و مقادیری که با سرعت زیاد تغییر میکنند را هم با دقت بالایی بازتولید میکند.
اگر این مطلب برای شما مفید بوده است، آموزشهای زیر نیز به شما پیشنهاد میشوند:
- مجموعه آموزشهای مهندسی مخابرات
- آموزش مخابرات ۱
- مجموعه آموزشهای مهندسی الکترونیک
- آموزش مبانی الکترونیک – مفاهیم تئوریک به همراه شبیه سازی عملی و کاربردی
- مدولاسیون SSBSC چیست؟ — به زبان ساده
- گزینندگی کانال مجاور یا ACS در مخابرات چیست؟ — از صفر تا صد
- مدولاسیون کلیدزنی شیفت فاز یا PSK چیست؟ — از صفر تا صد
^^












