جمعکنندهی باینری — به زبان ساده (+ دانلود فیلم آموزش گام به گام)
«جمعکنندهی باینری» (Binary Adder) یکی از مدارهای ترکیبی پرکاربرد و سودمند است. این مدار دو یا چند عدد باینری را با یکدیگر جمع کرده و در خروجی قرار میدهد. جمعکنندهی باینری را میتوان به راحتی و با استفاده از چند گیت منطقی ساده پیادهسازی کرد.
سادهترین مدار جمعکنندهی باینری از چند گیت AND و XOR ساخته میشود؛ این مدار حاصل جمع دو بیت A و B را در خروجی قرار میدهد.
با توجه به قوانین مربوط به جمع اعداد باینری، پس از جمع A و B دو بیت خروجی SUM و CARRY یا Carry-out) COUT) تولید میشود. مهمترین کاربرد جمعکنندهی باینری در مدارهای حسابی و شمارشی است. برای درک بهتر این موضوع، فرآیند جمع دو عدد دهدهی زیر را در نظر بگیرید:

- بخشهای اول، دوم، سوم، چهارم، پنجم و ششم این مجموعه مطلب را میتوانید با کلیک روی هر یک از لینکهای مربوطه مطالعه کنید.
میدانیم هر کدام از ارقام با توجه به جایگاهی که دارند، وزن مخصوص به خود را نیز خواهند داشت. لذا برای جمع دو عدد که زیر یکدیگر نوشته شدهاند، از سمت راستترین ارقام شروع کرده و با حرکت به سمت چپ، ارقام را دوتا دوتا با یکدیگر جمع میکنیم.
پس از جمع دو رقمی که در یک ستون و زیر هم قرار دارند، اگر حاصل جمع بزرگتر از 10 (مبنای عدد) باشد، رقم با وزن کمتر به عنوان SUM در همان ستون نوشته میشود اما رقم پر وزنتر به عنوان رقم «نقلی» (CARRY) به ستون سمت چپ انتقال مییابد. این فرآیند تا آخرین ستون به همین شکل ادامه مییابد.
برای جمع اعداد باینری نیز از همان قوانین اعداد دهدهی استفاده میشود، اما در این اعداد تنها وقتی بیت نقلی تولید میشود که حاصل جمع ستونها بزرگتر مساوی 2 (مبنای اعداد باینری) باشد. به عبارت دیگر تنها جمع 1 + 1 بیت نقلی تولید خواهد کرد.
جمع باینری
همانگونه که اشاره شد قوانین جمع باینری همانند جمع دهدهی است، با این تفاوت که اعداد باینری تنها دو رقم مختلف 0 و 1 دارند. لذا در هنگام جمع اعداد باینری، اگر SUM تولید شده بزرگتر مساوی 2 (1 + 1) باشد، یک بیت نقلی نیز خواهیم داشت. این بیت نقلی برای جمعهای بعدی به ستون سمت چپ منتقل میشود. برای درک بهتر این موضوع، جمع تک بیتی زیر را در نظر بگیرید.
جمع باینری دو بیت

در هنگام جمع دو عدد تک بیتی A و B با یکدیگر، حاصل «0 + 0»، «0 + 1» و «1 + 0» 0 یا 1 خواهد بود. اما همانگونه که در آخرین ستون نشان داده شده حاصل «1 + 1» مساوی 2 یا عدد باینری 10 میشود؛ یعنی SUM = 0 و CARRY = 1 میگردد.
بلوک دیاگرام زیر یک جمعکنندهی ساده را نشان میدهد. در این جمعکننده دو ورودی تک بیتی A و B با یکدیگر جمع شده و خروجیهای S) Sum) و C) Carry) تولید میشوند.
بلوک دیاگرام جمعکنندهی باینری

در مثال تک بیتی قبلی میتوان از بیت نقلی تولید شده صرف نظر کرد. ممکن است شما نیز توجه کرده باشید که حاصل جمع هر دو بیت (Sum) با حاصل XOR آنها برابر است. فرضاً اگر این دو بیت را A و B بنامیم، خروجی جدول درستی تابع XOR با مجموع این دو بیت برابر است.
گیت XOR با 2 ورودی

میبینیم که درست مانند عملیات جمع باینری، خروجی گیت XOR نیز تنها در صورتی 1 خواهد بود که یکی از ورودیها 1 و دیگری 0 باشد. تا بدین جای کار توانستهایم خروجی Sum را تولید کنیم؛ اما در سیستمهای میکروپروسسوری و ماشین حسابهای الکترونیکی، به مقدار Carry تولید شده نیز نیاز داریم. برای یافتن معادلهی تولید Carry، مثال قبلی را بازنویسی میکنیم تا شامل 2 بیت خروجی باشد.

از معادلات بالا درمییابیم خروجی گیت XOR تنها در صورتی 1 میشود که فقط یکی از ورودیها 1 باشد. اما از طرفی خروجی Carry تنها زمانی 1 است که هر دو ورودی A و B یک باشند. مناسبترین گیت منطقی برای این کار گیت AND است، چرا که خروجی AND نیز تنها در صورتی HIGH میشود که هر دو ورودی آن HIGH باشند.
گیت AND با 2 ورودی

بدین ترتیب با ترکیب گیتهای AND و XOR میتوان یک جمعکنندهی باینری ساده ساخت. مدار ساخته شده به نام «نیم جمعکننده» (Half Adder) نیز شناخته میشود.
مدار نیم جمعکننده
نیم جمعکننده یک مدار منطقی است که به ورودی آن دو رقم باینری داده شده و در خروجی آن دو رقم باینری Sum و Carry تولید میشود.
جدول درستی نیم جمعکننده
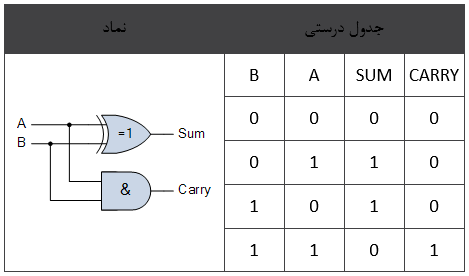
همانگونه که در جدول درستی بالا مشخص است، خروجی SUM از XOR شدن ورودیها و خروجی CARRY از AND شدن ورودیها به دست میآید. لذا عبارت بولی که برای توصیف نیم جمعکننده به کار میرود به صورت زیر خواهد بود.
برای بیت SUM داریم:
SUM = A XOR B = A ⊕ B
برای بیت CARRY داریم:
CARRY = A AND B = A.B
اما یکی از بزرگترین اشکالات مدارهای نیم جمعکننده که استفاده از آنها در جمعهای باینری را محدود میسازد، نبود پایهای برای رقم نقلی ورودی (Carry-in) از مدار قبلی در جمعهای چند بیتی است.
به عنوان مثال، فرض کنید میخواهیم دو دادهی 8 بیتی را با هم جمع کنیم. همانگونه که در مثالهای ابتدایی بررسی کردیم، از کم ارزشترین بیت (LSB) شروع کرده و دو بیت هم وزن را با یکدیگر جمع میکنیم. در جریان این عملیات باید هر بیت نقلی که ایجاد میشود به ستون سمت چپ انتقال یافته و با اعداد آن ستون جمع شود. لذا پس از اولین مرحله، در سایر مراحل بیت نقلی ورودی از مرحلهی قبل را نیز باید با دو بیت هموزن جمع کنیم. اما از آنجایی که نیم جمعکننده تنها 2 پایهی ورودی دارد، در پیچیدهترین حالت میتواند حاصل 1 + 1 را حساب کند و در صورت وجود بیت نقلی ورودی، خروجی به دست آمده اشتباه خواهد بود. برای رفع این مشکل، مدارهای «تمام جمعکننده» (Full Adder) طراحی شدهاند.
مدار تمام جمعکننده
مهمترین تفاوت تمام جمعکننده با نیم جمعکننده داشتن سه ورودی است. همانگونه که در شکل زیر نشان داده شده، ورودیهای تمام جمعکننده عبارتند از دو بیت دادهی A و B و یک C-in) Carry-in) که برای دریافت بیت نقلی از مرحلهی قبلی مدار به کار میرود.
بلوک دیاگرام تمام جمعکننده

با این اوصاف، تمام جمعکننده یک مدار منطقی است که سه بیت را با یکدیگر جمع میکند. همانند نیم جمعکننده، در تمام جمعکننده نیز یک بیت نقلی خروجی تولید میشود که در جمعهای چند بیتی برای مراحل بعدی جمع کاربرد دارد. به طور کلی، Carry-in رقم نقلی است که از رقم کم ارزشتر گرفته میشود؛ در حالی که Carry-out نشانگر رقم نقلیای است که به رقم با ارزشتر منتقل میشود.
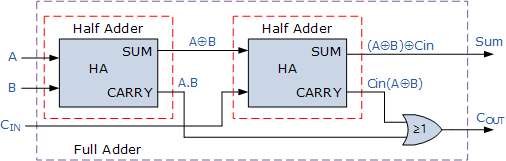
تمام جمعکننده را میتوان به صورت دو نیم جمعکننده در نظر گرفت که به یکدیگر متصل شدهاند، در این توصیف بیت نقلی تولید شده توسط اولین نیم جمعکننده بهگونهای که در پایین نشان داده شده به دومین نیم جمعکننده منتقل میشود.
دیاگرام منطقی تمام جمعکننده
از آنجایی که تمام جمعکنندهی بالا اساساً از دو نیم جمعکننده ساخته شده، جدول درستی آن علاوه بر خروجیهای S و COUT) Carry-out) و ورودیهای A و B، ستون دیگری نیز برای ورودی CIN) Carry-in) خواهد داشت.
جدول درستی تمام جمعکننده
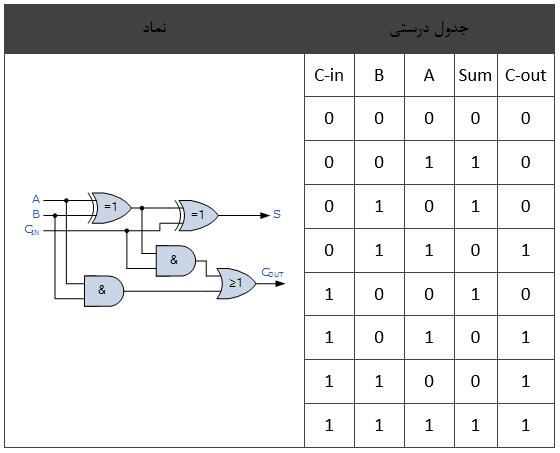
لذا عبارت بولی که برای توصیف تمام جمعکننده به کار میرود به صورت زیر خواهد بود.
برای بیت S) Sum) داریم:
SUM = (A XOR B) XOR Cin = (A ⊕ B) ⊕ Cin
برای بیت COUT) Carry-out) داریم:
CARRY-OUT = A AND B OR Cin(A XOR B) = A.B + Cin(A ⊕ B)
جمعکنندهی باینری n بیتی
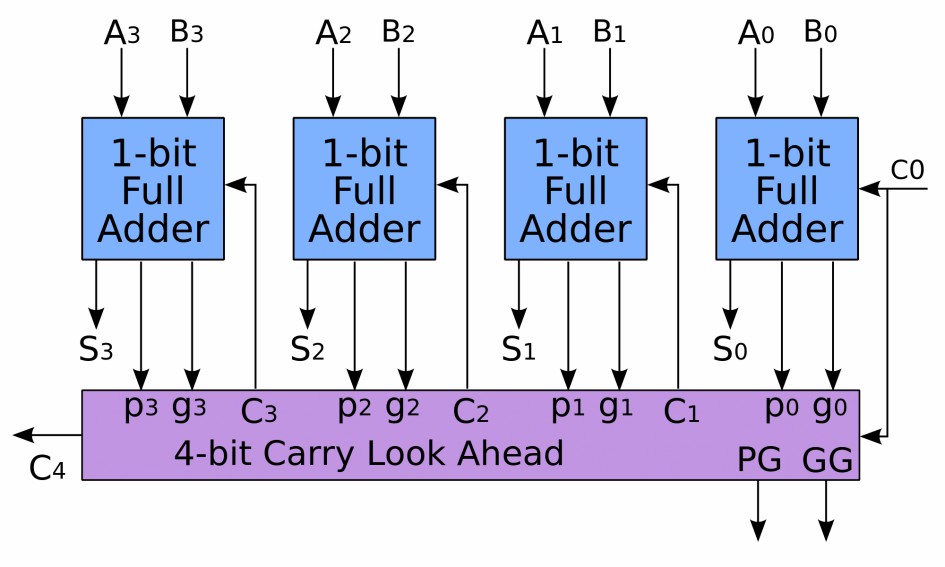
همانگونه که دیدیم جمعکنندههای تک بیتی را میتوان با استفاده از گیتهای منطقی پایه ساخت. اما به طور کلی اگر بخواهیم دو عدد n بیتی را با هم جمع کنیم، باید n تمام جمعکننده را با یکدیگر متصل یا «کَسکِد» (cascade) کنیم. با این کار یک «جمعکننده با نقلی موجی» (Ripple Carry Adder) ساختهایم.
یک جمعکنندهی Ripple Carry از n تمام جمعکنندهی 1 بیتی که با یکدیگر کَسکِد شدهاند ساخته میشود. در این جمعکنندهها، هر یک از تمام جمعکنندهها نشاندهندهی یک ستون وزندار هستند. از آنجایی که ارقام نقلی با حرکت درون تمام جمعکنندهها و از راست به چپ (از LSB به MSB) یک اثر موج گونه تولید میکنند، لذا به اینگونه جمعکنندهها، «جمعکننده با نقلی موجی» گفته میشود.
به عنوان مثال فرض کنید میخواهیم دو عدد 4 بیتی را با یکدیگر جمع کنیم. خروجیهای اولین تمام جمعکننده عبارتند از S که اولین رقم حاصل جمع است و Cout که رقم نقلی خروجی است و به عنوان Cin یا رقم نقلی ورودی برای تمام جمعکنندهی بعدی استفاده میشود.
در زنجیرهی تمام جمعکنندهها، دومین جمعکننده نیز یک خروجی S تولید میکند که دومین رقم حاصل جمع به شمار میرود و Cout آن نیز به تمام جمعکنندهی بعدی منتقل میشود. به همین ترتیب میتوان با اتصال بیت نقلی خروجی طبقهی پایینتر به بیت نقلی ورودی طبقهی بالاتر، جمعکنندههای چندبیتی بزرگتری ساخت. شکل زیر اتصالات بین تمام جمعکنندهها در یک جمعکنندهی 4 بیتی را نشان میدهد.
جمعکنندهی 4 بیتی Ripple Carry

یکی از بزرگترین اشکالات کسکد کردن جمعکنندههای 1 بیتی برای جمع اعداد باینری بزرگ این است که اگر مقدار ورودیهای A و B تغییر کند، حاصل جمعی که در خروجی قرار میگیرد تا زمان انتقال کامل ارقام نقلی از طریق همهی تمام جمعکنندهها تغییر نخواهد کرد؛ چرا که مدتی طول میکشد تا هرگونه تغییر در نقلی ورودی کم ارزشترین بیت (LSB)، به باارزشترین بیت (MSB) حاصل جمع اعمال شود. بنابراین جمعکننده با مقداری تأخیر به هرگونه تغییر در ورودیها پاسخ خواهد داد.
اگر سرعت جمعکننده اهمیتی نداشته باشد و یا تعداد بیتهایی که با یکدگیر جمع میشوند زیاد نباشد، مثلا 4 بیت یا 8 بیت، میتوانیم از این تأخیر چشمپوشی کنیم. اما اگر بخواهیم عملیات جمع را با کلاک بالا و سریع انجام دهیم و یا اینکه تعداد بیتها از 32 یا 64 بیت بیشتر باشد، تأخیر موجود به قدری زیاد خواهد بود که عملیات جمع به درستی و با یک کلاک پایان نخواهد یافت.
این تأخیر ناخواسته «تأخیر انتشار» (Propagation delay) نامیده میشود. همچنین هنگامی که حاصل جمع دو عدد n بیتی بزرگتر مساوی 2n باشد، خطای «سرریز» (overflow) رخ میدهد.
یکی از راه حلهایی که برای حذف تأخیر انتشار ارائه شدهاست «جمعکنندهی Carry Look Ahead» نام دارد. در این جمعکننده به جای استفاده از آرایش موجی ذکر شده، سیگنالهای Cin مستقیماً از ورودیهای A و B تولید میشوند. با به کارگیری منطق carry-look ahead سرعت جمعکنندهی موازی به شدت بهبود مییابد.
مدت زمانی که یک جمعکنندهی Carry Look Ahead برای تولید SUM صحیح نیاز دارد، مستقل از تعداد بیتهای دادههای استفاده شده در عملیات است. برخلاف Ripple Adder ها که زمان لازم برای تکمیل عملیات جمع، رابطهی مستقیمی با تعداد بیتهای اعداد ورودی دارد.
مدارهای جمعکنندهی 4 بیتی از نوع carry look ahead به صورت آیسیهای استاندارد موجودند. به عنوان مثال آیسیهای 74LS83 و74LS283 از نوع TTL و آیسی 4008 از نوع CMOS بوده که دو عدد 4 بیتی را با یکدیگر جمع کرده و مطابق شکل زیر دو خروجی SUM و CARRY تولید میکنند.
نماد منطقی 74LS83

خلاصه
در این آموزش دربارهی جمعکنندههای باینری صحبت کردیم. مدارهای جمعکننده برای جمع دو عدد باینری و به دست آوردن حاصل جمع و رقم نقلی خروجی (carry-out) به کار میروند. سادهترین جمعکنندهها با اتصال گیتهای XOR و AND ساخته میشوند که به آنها نیم جمعکننده گفته میشود. با ترکیب دو نیم جمعکننده، یک تمام جمعکننده ساخته میشود.
آیسیهای 74LS283 و CD4008 از جمله آیسیهای تمام جمعکنندهی 4 بیتی هستند. این آیسیها دو عدد 4 بیتی با یکدیگر جمع کرده و علاوه بر بیت نقلی خروجی، دارای یک پایه برای بیت نقلی ورودی هستند. میتوان با استفاده از این دو پایه و اتصال آبشاری (cascade) این آیسیها، جمعکنندههای 8 بیتی، 12 بیتی، 16 بیتی و ... ساخت. البته در اینگونه موارد بایستی به «تاخیر انتشار بیت نقلی» توجه داشت که ممکن است در جمعکنندههایی با تعداد بیت زیاد مشکل ایجاد کند.
بخش بعدی مجموعه مقالات «منطق ترکیبی» بلاگ فرادرس را میتوانید از طریق این لینک مطالعه کنید؛ اگر مطلب بالا برای شما مفید بوده است، ممکن است آموزشهای زیر نیز برایتان کاربردی باشند.
- مجموعه آموزش های مدارهای منطقی (طراحی دیجیتال)
- گنجینه فرادرس های آموزش الکترونیک دیجیتال و سیستم های برنامه پذیر
- مجموعه آموزشهای مهندسی برق
- آموزش جامع سیستمهای باینری
^^










اگر اون موزیک رو هم از کلیپ ها بردارید خیلی عالی میشه
سلام،نیم کری(نقلی)را هم توضیح دهید چیست،ممنون از مطالب مفید شما
مفید بود شکل مدار نیم جمع کننده رو میخواستم که استفاده شد