بسط دو جمله ای و قضیه آن — به زبان ساده

در ریاضیات بخصوص در جبر با «قضیه دو جمله‌ای» (Binomial Theorem) برخورد کرده‌اید. یک عبارت «دو جمله‌ای» (Binomial) حالتی خاصی از یک «چند جمله‌ای» (Polynomial) است و از قواعد آن پیروی می‌کند. ولی به علت استفاده زیاد از دو جمله‌ای‌ها در این مطلب به معرفی آن‌ها پرداخته و خصوصیاتشان را مرور می‌کنیم. گاهی به قضیه دو جمله‌ای، «بسط دو جمله‌ای» (Binomial Expansion) نیز می‌گویند.

برای آگاهی و آشنایی بیشتر با چند جمله‌ای‌ها بهتر است مطلب چندجمله‌ای‌ها – به زبان ساده را بخوانید. البته مطالعه اصول شمارش و فاکتوریل — به زبان ساده نیز خالی از لطف نیست.

بسط دو جمله‌ای

یک دو جمله‌ای همان چند جمله‌ای است که دارای دو «عبارت» یا «جمله» (Term) است.

فیلم آموزش آمادگی برای آزمون جی مت GMAT در فرادرس

کلیک کنید

به عنوان مثال عبارت زیر یک دو جمله‌ای برحسب y است.

$$\large 5y^3-3$$

در اینجا، $$5y^3$$ را جمله اول و $$3$$ را جمله دوم می‌نامند زیرا به وسیله علامت + یا - از یکدیگر جدا شده‌اند. به این ترتیب این دو جمله‌ای براساس تفاضل دو عبارت یا جمله نوشته شده است. از آنجایی که بزرگترین درجه این دوجمله‌ای برحسب y، مقدار ۳ است، آن را «دو جمله‌ای درجه ۳» (Binomial Degree 3) می‌گویند.

حال یک عبارت دو جمله‌ای مانند $$a+b$$ را در نظر بگیرید. اگر این عبارت را در خودش ضرب کنیم، حاصل چه خواهد بود؟ آیا برای این حاصل‌ضرب، الگویی خاصی برحسب جمله‌ها وجود دارد؟ اگر ضرب را تکرار کنیم، چطور؟

قضیه دو جمله‌ای به این پرسش پاسخ می‌دهد. در ادامه توان‌های ۲، ۳ و ۴ عبارت $$a+b$$ را نوشته‌ایم تا بتوانیم الگوی این جملات را تشخیص دهیم. مشخص است که منظور از توان ۲، ضرب عبارت در خودش است. همچنین توان ۳ و ۴ نیز نشان دهنده سه یا چهار بار ضرب عبارت در خودش خواهد بود.

مربع دوجمله‌ای (توان ۲):

$$\large (a+b)(a+b)=(a+b)^2=a^2+ab+ba+b^2=a^2+2ab+b^2$$

مکعب دوجمله‌ای (توان ۳):

$$\large (a+b)(a+b)(a+b)=(a+b)^3=(a^2+2ab+b^2)(a+b)=$$

$$\large a^3+a^2b+2a^2b+2ab^2+ab^2+b^3=a^3+3a^2b+3ab^2+b^3$$

توان ۴:

$$\large (a+b)(a+b)(a+b)(a+b)=(a+b)^4=(a+b)^2(a+b)^2=$$

$$\large (a^2+ab+ba+b^2)(a^2+ab+ba+b^2)=$$

$$\large a^4+4a^3b+6a^2b^2+4ab^3+b^4$$

به این ترتیب، هرچه توان افزایش یابد، تعداد جملات نیز بیشتر خواهد شد. مشخص است که برای توان ۲ تعداد جملات برابر با ۳ و برای توان ۳، تعداد جملات برابر با ۴ و برای توان ۴ نیز تعداد جملات برابر با ۵ است. بنابراین همیشه تعداد جملات یکی بیشتر از مقدار توان خواهد بود. به این ترتیب اگر $$n$$ نشان‌دهنده توان مربوط به دو جمله‌ای باشد، تعداد جملات برای بسط دو جمله‌ای با توان $$n$$ برابر با $$n+1$$ خواهد بود.

برای شناخت الگو‌هایی ساخته شده در این حالت، بهتر است به ادامه مطلب توجه کنید.

الگوی توانی

برای مثال مکعب عبارت $$(a+b)$$ را در نظر بگیرید. در تصویر زیر الگوی مربوط به توان‌های جمله $$a$$ دیده می‌شود.

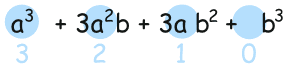
همچنین توان‌های مربوط به عبارت $$b$$ را در تصویر زیر می‌بینید.

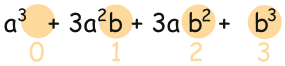
به همین ترتیب اگر $$n$$ توان دو جمله‌ای و $$k$$ نیز توان جمله $$b$$ و $$n-k$$ توان جمله $$a$$ را نشان دهد، خواهیم داشت:

بنابراین به نظر می‌رسد می‌توان الگوی زیر را برای توان‌های هر جمله در نظر گرفت.

$$\large a^{n-k}b^k$$

الگوی ضرایب

براساس الگوی معرفی شده برای توان‌ها توانستیم تا حدودی، دو جمله‌ای را بسط بدهیم. ولی در مرحله بعدی احتیاج است که الگوی ضرایب را نیز ایجاد کنیم. در تصویر زیر ضرایب مربوط به توان‌های ۰ تا ۳ دو جمله‌ای به ترتیب سطری، دیده می‌شوند.

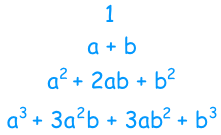
البته توجه داشته باشید در تصویر بالا ضریب ۱ برای هر جمله نوشته نشده، زیرا عدد ۱ در ضرب بی‌تاثیر است. به نظر می‌رسد که این ضرایب نیز دارای الگوی خاصی هستند. به تصویر زیر نگاه کنید.

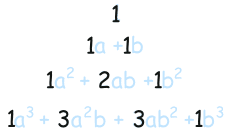
این الگو به مثلث خیام-پاسکال معروف است. در این مثلث هر عدد از جمع دو عضو بالاسری خود حاصل می‌شود. برای مثال اگر بخواهیم ضرایب مربوط به بسط دو جمله‌ای با توان ۴ را بنویسیم خواهیم داشت:

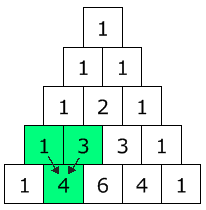
بنابراین به راحتی می‌توان بسط یک دو جمله‌ای درجه ۴ را برحسب الگوی ضرایب و توان‌ها نوشت.

$$\large (a+b)^4=a^4+4a^3b+6a^2b^2+4ab^3+b^4$$

در زیر یک نمونه از مثلث خیام-پاسکال را می‌بینید.

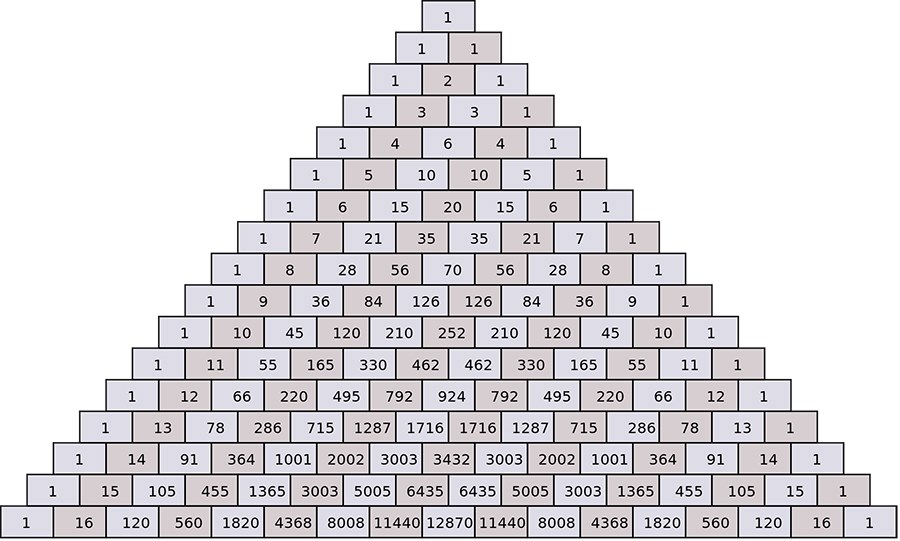
به این ترتیب می‌توان بسط دو جمله‌ای درجه ۵ را به صورت زیر محاسبه کرد.

$$\large (a+b)^5=a^5+5a^4b+10a^3b^2+10a^2b^3+5ab^4+b^5$$

بسط دو جمله‌ای

قضیه یا بسط دو جمله‌ای را در ادامه خواهید دید. همچنین با کاربردهای این قضیه نیز بیشتر آشنا خواهید شد.

قضیه دو جمله‌ای:

اگر n‌ عددی طبیعی (مثبت) باشد، تساوی زیر برای هر $$a$$ و $$b$$ برقرار است.

$$\large (a+b)^n=\sum_{k=0}^n {n \choose k}a^{n-k}b^k$$

که در آن ترکیب $$k$$ از $$n$$ که به صورت $${ n \choose k}$$ نشان داده می‌شود، توسط رابطه زیر قابل محاسبه است. این ضرایب کاملا با ضرایب حاصل از مثلث خیام-پاسکال مطابقت دارند.

$$\large {n \choose k}=\dfrac{n!}{k!(n-k)!}$$

حتما به یاد دارید که علامت ! نیز نشان دهنده فاکتوریل یک عدد طبیعی است. بنابراین برای $$k=0$$، ضریب جمله اول و برای $$k=1$$، ضریب جمله دوم و ... برای $$k+1$$ ضریب جمله kام قابل محاسبه است. برای مثال اگر بخواهیم ضریب جمله پنجم یعنی $$k+1=5$$ را در بسط دو جمله‌ای درجه ۶، بنویسیم باید مقدار $$k$$ را برابر با ۴ در نظر گرفته و به صورت زیر عمل کنیم.

$$\large {6 \choose 4}=\dfrac{6!}{4!(6-4)!}=\dfrac{6\times 5\times 4\times 3\times 2\times 1}{(4 \times 3\times 2\times 1)(2 \times 1)}=15$$

مثال 1

بسط دو جمله‌ای $$(x+y)^6$$ را براساس رابطه بالا به صورت زیر خواهیم نوشت:

$$\large (x+y)^6=\sum_{k=0}^6 {6 \choose k}x^{6-k}y^k=$$

$$\large {6 \choose 0}x^{6-0}y^0+{6 \choose 1}x^{6-1}y^1+{6 \choose 2}x^{6-2}y^2+{6 \choose 3}x^{6-3}y^3+$$

$$\large {6 \choose 4}x^{6-4}y^4+{6 \choose 5}x^{6-5}y^5+{6 \choose 6}x^{6-6}y^6=$$

$$\large x^6+6x^5y^1+15x^4y^2+20x^3y^3+15x^2y^4+6xy^5+y^6$$

مثال 2

ضرایب بسط دو جمله‌ای $$(2x+4)^8$$ برای عبارت $$x^3$$ در ادامه مورد بررسی قرار گرفته است.

با توجه به توان این عبارت که برابر با ۳ است، مشخص می‌شود که مربوط به جمله ششم بسط خواهد بود، زیرا می‌دانیم توان‌های مربوط به جمله اول به صورت $$n-k$$ نوشته می‌شوند. از آنجایی که در این حالت $$n=8$$ و $$n-k=3$$ است، در نتیجه مشخص می‌شود که باید ضرایب جمله ششم ($$k+1=6$$) برای عبارت اول ($$2x$$) را پیدا کنیم. در نتیجه می‌توان نوشت:

$$\large {8 \choose 5} =\dfrac{8!}{5!(8-5)!}=\dfrac{8\times 7 \times 6}{3\times 2}=56$$

بنابراین می‌توان جمله چهارم را به صورت زیر نوشت:

$$\large 56 (2x)^3(4)^5= 56 \times 8 \times 1024\times x^3=458752x^3$$

مثال 3

به کمک بسط دو جمله‌ای می‌توان نشان داد که در توزیع دو جمله‌ای (Binomial Distribution) مجموع احتمالات روی تکیه‌گاه متغیر تصادفی برابر با ۱ است. زیرا:

$$\large \sum_{k=0}^n P(X=x)=\sum_{x=0}^n {n \choose x}p^x(1-p)^{n-x}=(p+(1-p))^n=1^n=1$$

تفسیر هندسی قضیه دو جمله‌ای

برای نمایش قضیه یا بسط دو جمله‌ای می‌توان از هندسه نیز کمک گرفت. فرض کنید که $$a$$ ضلع یک مربع است. مشخص است که مساحت چنین مربعی برابر با $$a^2$$ است.

فیلم آموزش قضیه بسط دو جمله ای و مثلث خیام (رایگان) در فرادرس

کلیک کنید

حال اگر به اضلاع این مربع، مقدار $$b$$ واحد اضافه کنیم، مساحت چنین مربعی به صورت $$(a+b)^2$$ نوشته می‌شود. رابطه بین مساحت مربع اولیه و مربع ثانویه، طبق تصویر زیر قابل نمایش است.

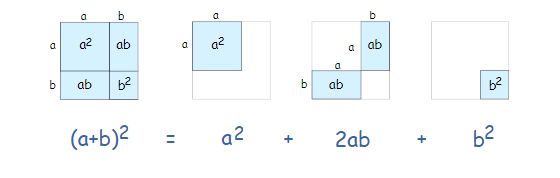
به همین ترتیب می‌توان برای مکعب یا توان ۳ نیز بسط دو جمله‌ای را به روش هندسی نمایش داد. به مانند حالت قبل، یک مکعب مربع با ضلع $$a$$ در نظر بگیرید که دارای حجم $$a^3$$ است. اگر به اضلاع این مکعب، مقدار $$b$$ واحد اضافه کنیم رابطه‌ هندسی و ریاضی به صورت تصویر زیر خواهد بود.

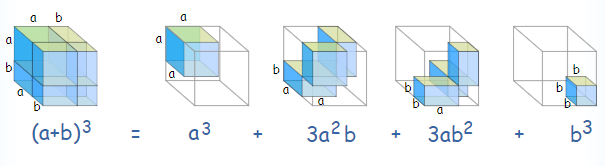
نکته: رابطه برای توان ۴ نیز به همین گونه خواهد بود ولی از آنجایی که در نمایش بعد چهارم دچار مشکل هستیم، از ترسیم شکل معذوریم.

محاسبه عدد اویلر ($$\large e$$)

براساس قضیه دو جمله‌ای می‌توان مقدار عدد e یا «عدد اویلر» (Euler's Number) را یافت. می‌دانیم که این عدد به صورت $$e=2.718281828459045...$$ نوشته می‌شود. مشخص است که این عدد دوره گردش ندارد، پس الگوی تکراری برای ارقام آن نمی‌توان پیدا کرد. یعنی به صورت نسبت دو صحیح قابل نوشتن نیست. در حقیقت این عدد بسط دو جمله‌ای برای عبارت زیر است، زمانی که مقدار $$n$$‌ خیلی خیلی بزرگ باشد یا به بی‌نهایت میل کند.

$$\large (x+\frac{1}{n})^n$$

براساس قضیه یا بسط دو جمله‌های برای این رابطه خواهیم داشت:

$$\large (x+\frac{1}{n})^n=\sum_{k=0}^n{ n \choose k}1^{n-k}(\frac{1}{n})^k=\sum_{k=0}^n{ n \choose k}(\frac{1}{n})^k$$

از آنجایی که مقدار $$1^{n-k}=1$$ است، این جمله را حذف کرده‌ایم. حال سعی داریم، این رابطه را زمانی که $$n$$ به سمت بی‌نهایت میل می‌کند، محاسبه کنیم. در حقیقت به دنبال  حد در بی‌نهایت این تابع برحسب $$n$$ هستیم. حال رابطه را به صورت ساده‌تری می‌نویسیم.

$$\large \sum_{k=0}^n \dfrac{n!}{k!(n-k)!}.\dfrac{1}{n^k}$$

در تصویر زیر حد رابطه بالا در $$n\rightarrow \infty$$ توضیح داده شده است.

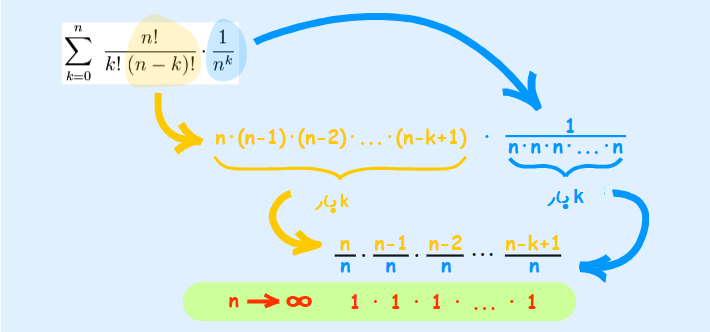
همانطور که دیده می‌شود، نسبت $$\frac{n!}{(n-k)!}$$ را می‌توان به صورت $$n.(n-1)(n-2)\cdots (n-k+1)$$ نوشت. به همین ترتیب نسبت این عبارت‌ها با $$n$$ نیز زمانی که $$n$$ به سمت بی‌نهایت میل کند، برابر با ۱ خواهد بود. پس تنها عبارت باقی مانده به شکل زیر نوشته خواهد شد.

$$\large \sum_{k=0}^n\dfrac{1}{k!}=\dfrac{1}{0!}+\dfrac{1}{1!}+\dfrac{1}{2!}+\dfrac{1}{3!}+\dfrac{1}{4!}+\ldots$$

با استفاده از چند جمله اول (تا جمله ۵ام) مقدار عدد اویلر برابر با 2.7166 خواهد بود.